R语言学习笔记
1.R语言介绍


2.R语言安装
官网:https://www.r-project.org/
CARN → 选择China中任意镜像站点 → Download R for Windows → base(二进制版本R基础软件)→
Download R-4.2.2 for Windows (76 megabytes, 64 bit)
3.Rstudio安装
https://posit.co/download/rstudio-desktop/
DOWNLOAD RSTUDIO → DOWNLOAD RSTUDIO DESKTOP FOR WINDOWS → RStudio
Desktop → DOWNLOAD RSTUDIO → DOWNLOAD RSTUDIO DESKTOP FOR WINDOWS
4.Rtoos安装(R包安装需要)
https://cran.r-project.org/bin/windows/Rtools/rtools43/rtools.html
→Rtools43 installer
5.基本操作
查看当前工作目录 :getwd()
设置工作目录 :setwd(dir = "路径")
注意:Rwindow语言路径使用’\’ 而R语言使用’/'
查看工作目录下的文件:list.files() 或者 dir()
查看帮助文档 :help.start();
函数详情 help(sum)
查看函数参数 args(函数名)
查看包帮助文档: help(package=包名vig)
> getwd()
[1] "C:/Users/xiaob/Desktop"
> setwd(dir = "C:/Users/xiaob/Desktop/Rwork")
> getwd()
[1] "C:/Users/xiaob/Desktop/Rwork"
> list.files()
character(0)
> dir()
character(0)
赋值符号 ‘<-’ (等号可以不推荐)
赋值给全局变量 ‘<<-’
> x<-2
> x
[1] 2
> x<<-5
> x
[1] 5
> z <- sum(1,2,3,4,5)
> z
[1] 15
> t <- min(1,2,3,4,5)
> t
[1] 1> ls() #查看所有变量
[1] "t" "x" "y" "z"
> ls.str() #查看所有变量和变量值
t : num 1
x : num 5
y : num 4
z : num 15
> str(x)num 5
> rm(x) #删除变量
> x
Error: object 'x' not found
> rm(t,y,z) #删除多个变量
> z
Error: object 'z' not found> x<-2
> y<-4
> z<-8
> ls()
[1] "x" "y" "z"
> rm(list = ls()) #删除当前所有变量
> ls()
character(0)上下移动光标选择命令
> history() #查看历史命令
> history(5) #查看最近5条命令
清除命令窗口:ctrl + L
注释:#
保存工作空间:> save.image()
退出R: >q()
6.R包
(一)安装
查看包:https://cran.r-project.org/web/views/
1.在线安装
安装包:>install.packages() #需要选择镜像站点
安装指定包 :>install.packages("包名")
会自动安装依赖包
查看所有本地包安装路径:>libPaths()
查看所有已安装包列表:>library()
手动更改镜像:Tools → Global option → Packages
2.GitHub安装
GitHub搜索包名
> install.packages("devtools")
> install.packages("remotes")
> devtools::install_github("仓库名/包名")
3.本地安装
github仓库先下载压缩包
> devtools::install_local("绝对路径")
#注意改反斜杠
(二)使用
载入包: library(包名) 或者 require(包名)
查看包帮助文档 >help(package="包名")
查看包基本信息 >library(help="包名")
输入包内索引名可以直接查看数据集(注意需要先载入)
library(vcd)
library(help="vcd")
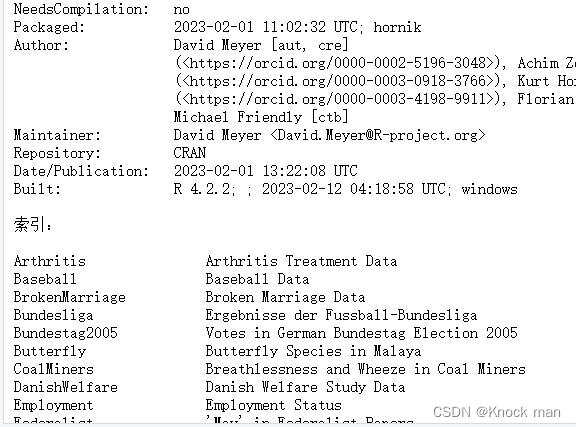
查看包内函数: ls("package:包名")
查看包内所有数据集 data(package="包名")
移除加载包: detach("package:包名")
查看当前已安装R包 installed.packages()
7.内置数据集
查看内置全部数据集 >help(package="datasets")
简略查看全部数据集 >data()
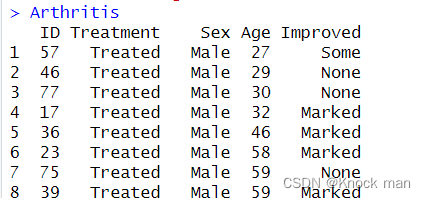
访问数据集:输入数据集名称
查看某个数据集详细信息:help("数据集名称")
8.数据结构
数据类型:


9.向量(集合)
1.基本操作
创建:>c(元素1,元素2,.....)
>x <- c(1,2,3,4)
>x
[1] 1 2 3 4#逻辑型向量必须大写
> z <- c(TRUE,T,F)
> z
[1] TRUE TRUE FALSE
> z <- c(True,T,F)
Error: object 'True' not found> c(1:20) #生成1到20的等差数列[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
[19] 19 20> seq(from=1,to=100,by=2) #生成步长为2的等差数列[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35
[19] 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71
[37] 73 75 77 79 81 83 85 87 89 91 93 95 97 99> seq(from=1,to=100,length.out=10) #生成十个值的等差数列[1] 1 12 23 34 45 56 67 78 89 100#向量化编程,批量计算
> x <- c(1,2,3,4,5)
> y <- c(6,7,8,9,10)
> x*2+y
[1] 8 11 14 17 20> x[x>3] #取出x中大于3的值
[1] 4 5
2.向量索引
R索引从1开始
> x <- c(1:10) #生成1到10的等差数列
> x[1] 1 2 3 4 5 6 7 8 9 10
> length(x) #集合长度
[1] 10
> x[3]
[1] 3
> x[-9] #不输出第9个元素
[1] 1 2 3 4 5 6 7 8 10> x[c(2:6)] #输出第2到第6个元素
[1] 2 3 4 5 6
> x[c(2,4,6)] #输出2,4,6元素
[1] 2 4 6> y <- c(1:5)
> y[c(T,F,T,T,F)] #只输出逻辑为真的值
[1] 1 3 4> y[y>2&y<5]
[1] 3 4> v <- c(1:3)
> v
[1] 1 2 3
> v[c(4,5,6)] <- c(4,5,6)
> v
[1] 1 2 3 4 5 6
> v[20] <- 4
> v[1] 1 2 3 4 5 6 NA NA NA NA NA NA NA NA NA NA NA NA NA 4
插入向量
> v <- c(1:5)
> v
[1] 1 2 3 4 5
> append(x = v,values = 99,after = 2) #在第二个元素后面插入99
[1] 1 2 99 3 4 5
rm(v) #删除整个向量
3.向量运算
> x <- 1:10
> x[1] 1 2 3 4 5 6 7 8 9 10
> x+1[1] 2 3 4 5 6 7 8 9 10 11
> x-3[1] -2 -1 0 1 2 3 4 5 6 7
> x <- x+1
> x[1] 2 3 4 5 6 7 8 9 10 11
> y <- seq(1,100,length.out = 10) #生成长度为10的等差数列
> y[1] 1 12 23 34 45 56 67 78 89 100
> x + y[1] 3 15 27 39 51 63 75 87 99 111
> x[1] 2 3 4 5 6 7 8 9 10 11
> y[1] 1 12 23 34 45 56 67 78 89 100
> x**y #x的y次幂[1] 2.000000e+00 5.314410e+05 7.036874e+13[4] 5.820766e+23 1.039456e+35 2.115876e+47[7] 3.213876e+60 2.697216e+74 1.000000e+89
[10] 1.378061e+104
> y%%x #取余运算[1] 1 0 3 4 3 0 3 6 9 1
> y%/%x #整除运算[1] 0 4 5 6 7 8 8 8 8 9#判断是否元素包含
> c(1,2,3) %in% c(1,2,2,4,5,6)
[1] TRUE TRUE FALSE
函数
> x <- -5:5
> x[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> abs(x) #绝对值[1] 5 4 3 2 1 0 1 2 3 4 5
> sqrt(x) #开根号[1] NaN NaN NaN NaN NaN 0.000000 1.000000 1.414214 1.732051 2.000000
[11] 2.236068
Warning message:
In sqrt(x) : NaNs produced
> sqrt(25) #开根号
[1] 5
> log(16,base=2) #2为底 16的对数
[1] 4
> log(16) #自然对数
[1] 2.772589> exp(x) #e的x次方[1] 6.737947e-03 1.831564e-02 4.978707e-02 1.353353e-01 3.678794e-01 1.000000e+00 2.718282e+00 7.389056e+00 2.008554e+01 5.459815e+01 1.484132e+02#ceiling(a) 返回不小于a的最小整数
> ceiling(c(-2.3,3.1415))
[1] -2 4#floor(x) 返回不大于x的最大整数
> floor(c(-2.3,3.1415))
[1] -3 3#trunc(x) 返回整数部分
> trunc(c(-2.3,3.1415))
[1] -2 3#roud(x,digits=保留小数位数) 对x四舍五入
> round(c(-2.3,3.1415))
[1] -2 3
> round(c(-2.3,3.1415),digits = 2)
[1] -2.30 3.14
#signif(x,digits=保留小数位数) 对x四舍五入 仅保留有效数字
> signif(c(-2.3,3.1415),digits=2)
[1] -2.3 3.1
> sin(x)[1] 0.9589243 0.7568025 -0.1411200 -0.9092974 -0.8414710 0.0000000 0.8414710 0.9092974[9] 0.1411200 -0.7568025 -0.9589243
> cos(x)[1] 0.2836622 -0.6536436 -0.9899925 -0.4161468 0.5403023 1.0000000 0.5403023 -0.4161468[9] -0.9899925 -0.6536436 0.2836622> vec <- 1:10
> vec[1] 1 2 3 4 5 6 7 8 9 10
> sum(vec)
[1] 55
> max(vec)
[1] 10
> min(vec)
[1] 1
> range(vec) #返回最大值最小值
[1] 1 10
> var(vec) #返回向量的方差
[1] 9.166667
相关文章:

R语言学习笔记
1.R语言介绍 2.R语言安装 官网:https://www.r-project.org/ CARN → 选择China中任意镜像站点 → Download R for Windows → base(二进制版本R基础软件)→ Download R-4.2.2 for Windows (76 megabytes, 64 bit) 3.Rstudio安装 https://po…...
【软件测试】企业测试面试题9道,从自我介绍到项目考察+回答......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、自我介绍 您好&a…...

《Spring源码深度分析》第8章 数据库连接JDBC
目录标题前言一、数据库连接方式1.JDBC连接数据库2.Spring Jdbc连接数据库(JdbcTemplate)二、JdbcTemplate源码分析1.update/save功能的实现源码分析入口(关键)基础方法execute1.获取数据库连接池2.应用用户设定的输入参数3. 调用回调函数处理4. 资源释放Update中的回调函数2.q…...

ModuleNotFoundError的解决方案【已解决】
问题描述 有包却提示ModuleNotFoundError 在正常情况下,你使用pip或者conda检查是否有相应包的时候,显示的是有的。但是一旦运行程序就会报这个ModuleNotFoundError错误。 问题可能是程序运行环境不对。 解决方案 (1)进入正确…...
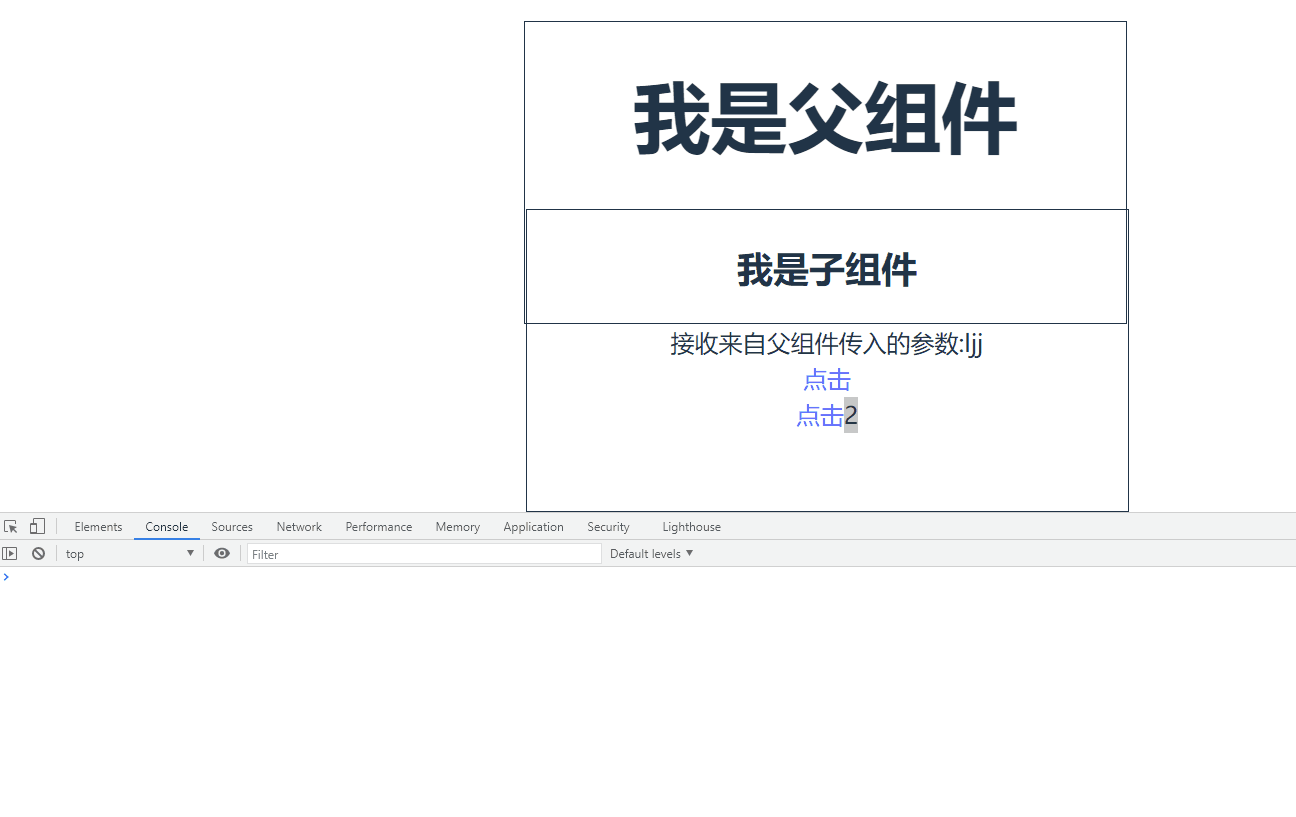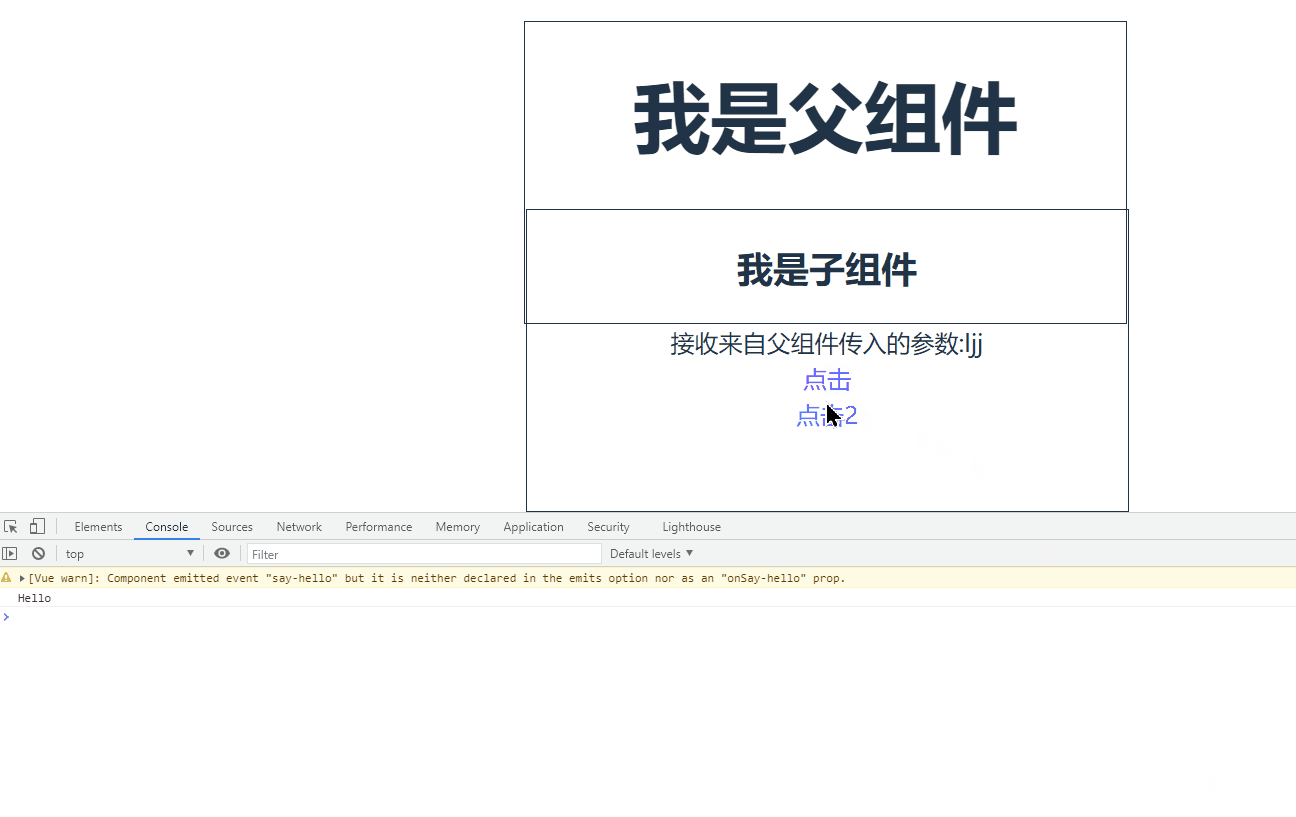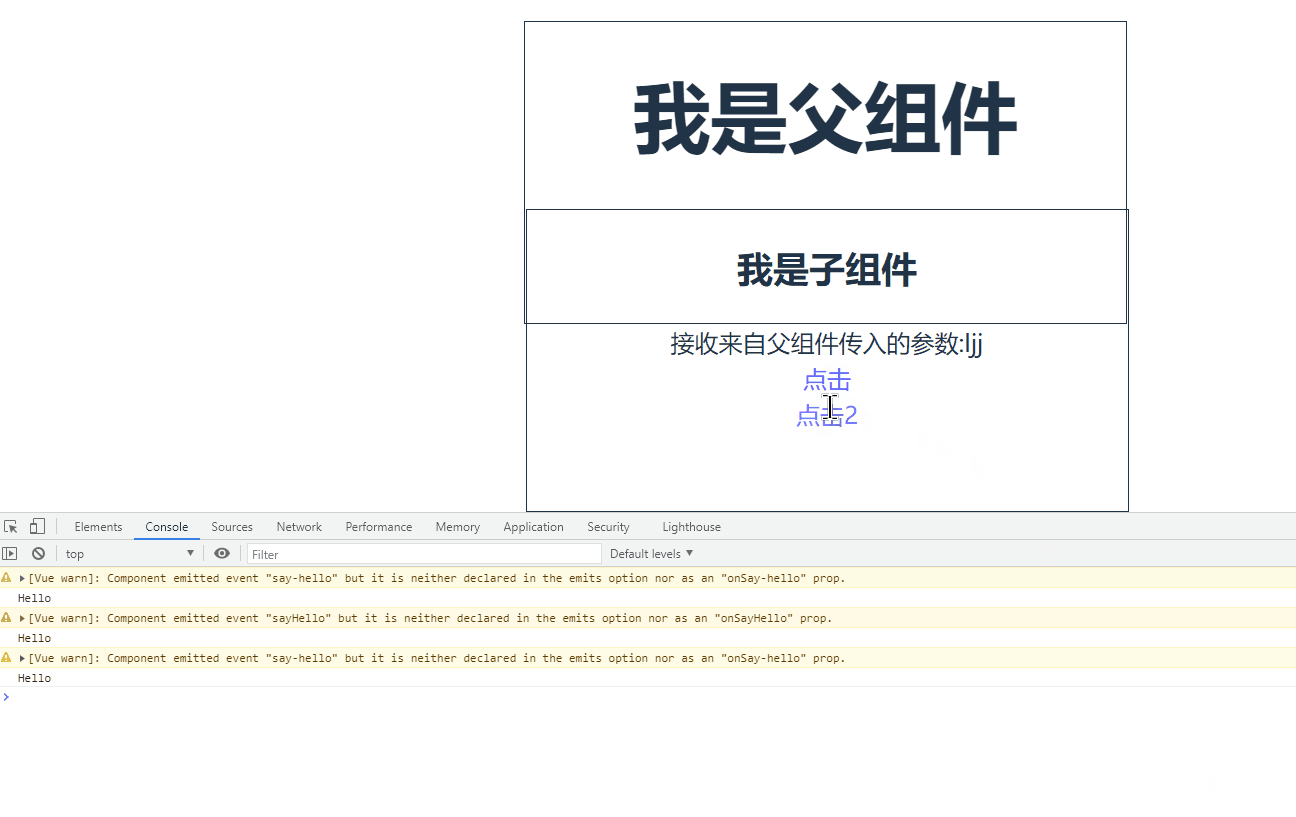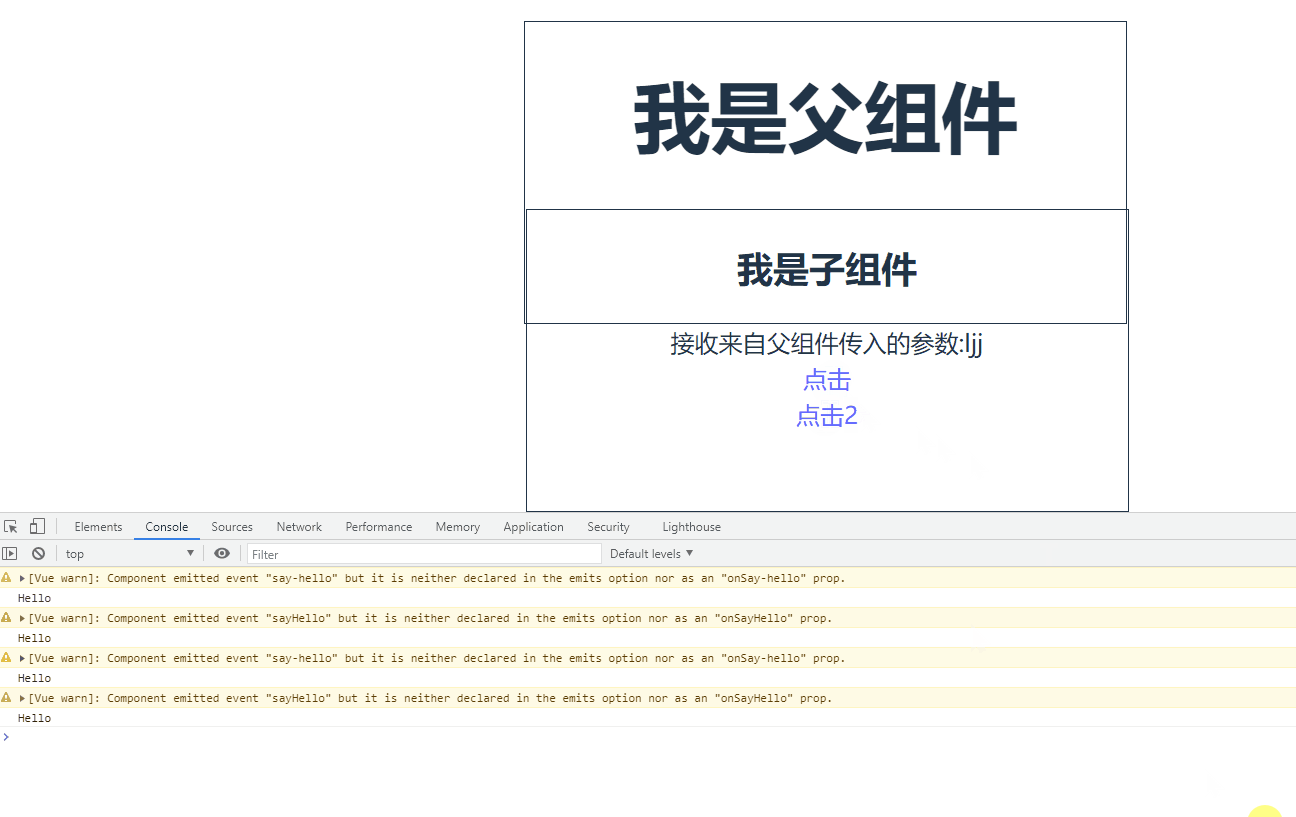
Vue驼峰与短横线分割命名中有哪些坑
目录 0.前言 驼峰和短横线分割命名注意事项 组件注册命名 父子组件数据传递时命名 父子组件函数传递 0.前言 Vue驼峰命名法指的是将变量以驼峰形式命名,例如 userName、userId 等,而短横线分隔符法则指的是用短横线分隔变量名,例如 user…...

从文件中加载数据以及异常处理
上期学习了数据的存储,这次学习数据的加载 你可以使用把openpyxl.load_workbook() 来打开一个已经存在的工作簿 >>> from openpyxl import load_workbook >>> wb load_workbook(filename empty_book.xlsx) >>> sheet_ranges wb[ran…...
【JavaSE】方法的使用
方法的使用BIT-5-方法的使用绪论1. 方法概念及使用1.1什么是方法1.2 方法定义1.3 实参和形参的关系(重要)1.4 没有返回值的方法2. 方法重载2.1 为什么需要方法重载2.2 方法重载概念3. 递归3.1 生活中的故事3.2 递归的概念3.2 递归执行过程分析3.3 递归练…...

ModelScope 垂类检测系列模型介绍
文章目录ModelScope介绍垂类模型介绍调用方式1 Demo Service2 Notebook3 本地使用* 二次开发总结ModelScope介绍 ModelScope 是阿里达摩院推出的 中文版模型即服务(MaaS, Model as a Service)共享平台。该平台在2022年的云栖大会上发布,之前…...
Linux | Linux卸载和安装MySQL(Ubuntu版)
最近又来到了Linux学习了,原因是要接触云服务器相关知识, 所以博主整理了一些关于Linux的知识, 欢迎各位朋友点赞收藏,天天开心丫,快乐写代码! Linux系列文章请戳 Linux教程专栏 目录 一、卸载MySQL 1…...
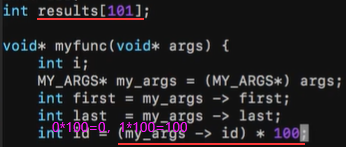
【C1】数据类型,常量变量,输入输出,运算符,if/switch/循环,/数组,指针,/结构体,文件操作,/编译预处理,gdb,makefile,线程
文章目录1.数据类型:单双引号,char(1B),int/float(32位系统,大小一样4B,但存储方式不同),double(8B),long double…...

【深度学习】pytorch的基础操作
import torch import numpy as np # 1.1 根据已有的数据创建张量 def test01(): # 1.1 创建标量 data torch.tensor(10) print(data) # 1.2 使用numpy数组来创建张量 data np.random.randn(2,3) data torch.tensor(data) print(data) # 1.3使用list…...
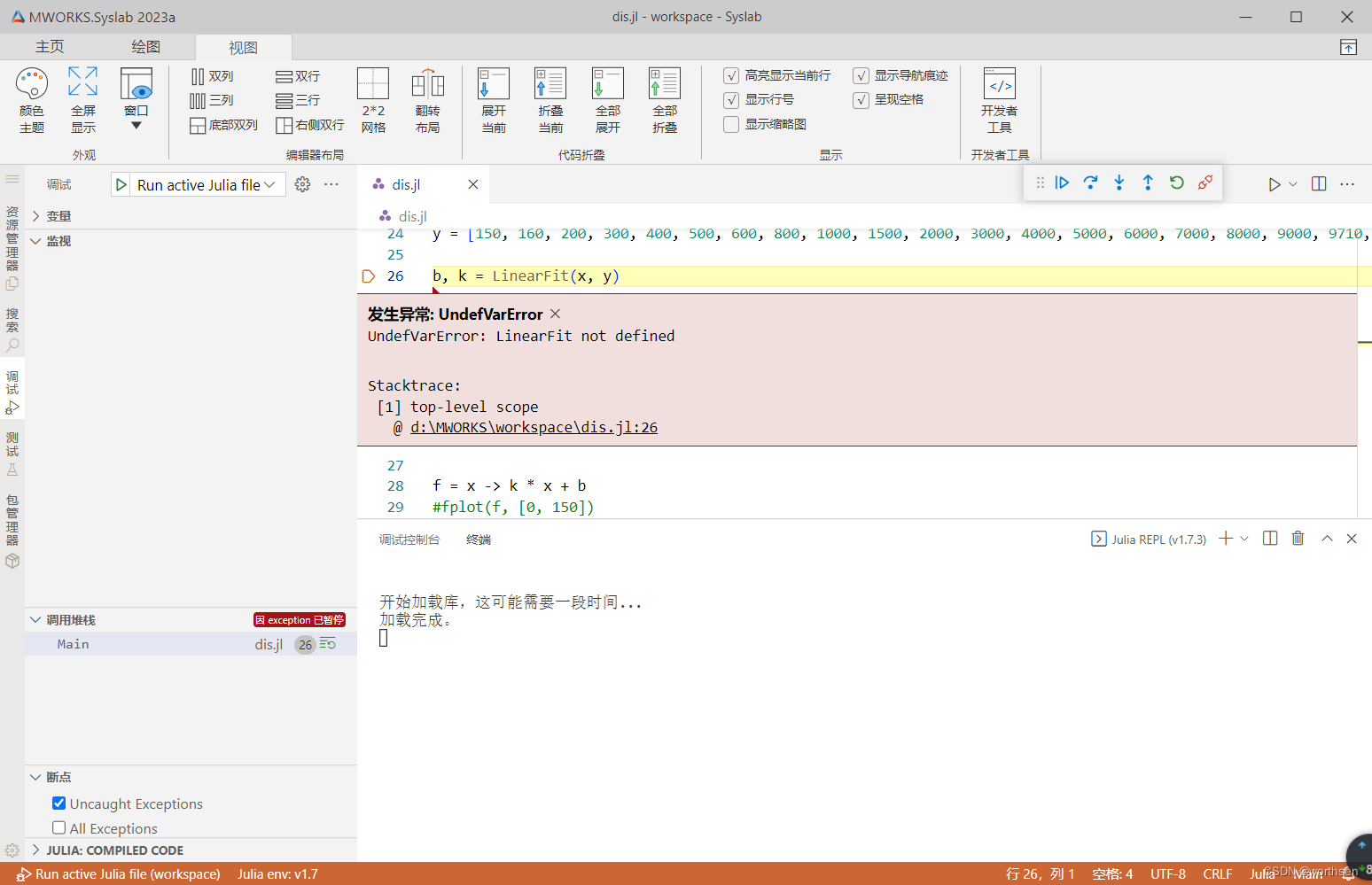
MWORKS--同元软控MWORKS介绍、安装与使用
MWORKS--同元软控MWORKS介绍、安装与使用1 同元软控介绍1.1 同元软控简介1.2 同元软控发展历史2 MWORKS介绍2.1 MWORKS简介2.2 MWORKS产品描述3 装备数字化3.1 发展3.2 内涵3.3 系统模型发展成为产品的一部分3.4 MWORKS系统模型数据管理3.4 MWORKS为装备数字化提供的套件4 下载…...
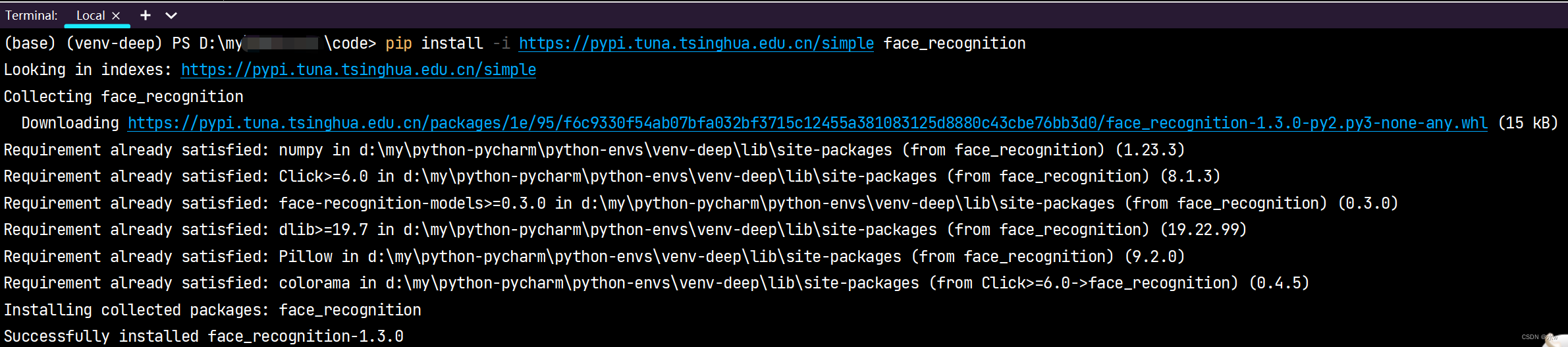
Python 解决dilb和face_recognition第三方包安装失败
目录 dilb和face_recognition第三方包安装失败 亲测有效的解决方法:whl安装方式 dilb和face_recognition第三方包安装失败 场景复现:因为需要用到dlibface_recognition,基于OpenCV做一些人脸识别的项目,在Pycharm中进行pip清华…...

Mac系统Mysql的8.0.22版本安装笔记和密码重置修改密码等问题方法
忘记密码官网教程地址:https://dev.mysql.com/doc/refman/5.7/en/resetting-permissions.html 5.7数据库安装指南参考:https://jingyan.baidu.com/article/fa4125ac0e3c2928ac709204.html 初次安装8.0.22遇到许多坑,密码修改失败;…...
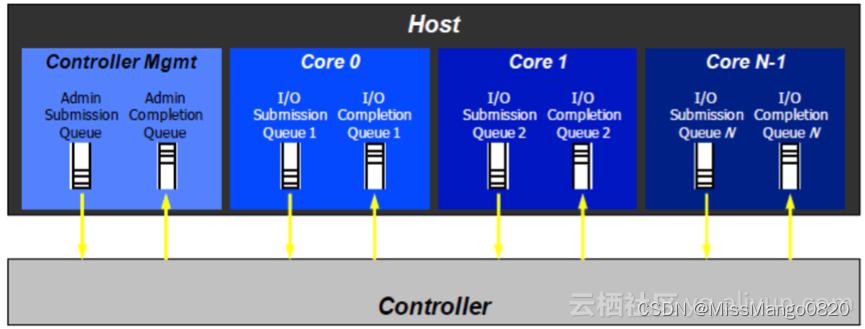
驱动 | Linux | NVMe 不完全总结
本文主要参考这里 1’ 2 的解析和 linux 源码 3。 此处推荐一个可以便捷查看 linux 源码的网站 bootlin 4。 更新:2022 / 02 / 11 驱动 | Linux | NVMe 不完全总结NVMe 的前世今生从系统角度看 NVMe 驱动NVMe CommandPCI 总线从架构角度看 NVMe 驱动NVMe 驱动的文件…...
一个测试人员,在现阶段的环境下如何在测试行业发展和自我价值。
前言周末和几个测试圈子里的大佬饭局上聊了一些职场和测试职业发展相关的话题,我将聊天的内容做了整理和阐述。。朋友圈有测试同学对这篇文章提了比较深刻的建议,下面是他的评价和建议:评价:据说是大佬饭桌总结,有两点…...
pwn手记录题2
fastbin_reverse_into_tcache(2.34) 本题所使用的libc版本为2.34;(最新版 libc2.34版本已经没有了所谓的hook函数,甚至exit_hook(实际为某个函数指针)也已经不能够使用;能够利用的手法已经很少了; 高版本glibc堆的几…...

CSS ~ 从入门到入坑。
CSS ~ 从入门到入坑。 文章目录CSS ~ 从入门到入坑。what。css 三种实现方式。选择器。id 选择器 > class 选择器 > 标签选择器。标签选择器。类选择器。id 选择器。层次选择器。后代选择器。子选择器。相邻兄弟选择器。通用选择器。结构伪类选择器。属性选择器。字体风格…...

成都哪家机构的Java培训比较好,求一个不坑的?
关于这个问题,相信你会得到很多条答案,以及很多家机构的自荐。既然如此,不如也了解一下老牌IT职业教育机构:有足够丰富的教学经验,丰富的教学产品资源以及成熟的就业保障体系,还有就是承担风险的能力。 很…...
《爆肝整理》保姆级系列教程python接口自动化(十二)--https请求(SSL)(详解)
简介 本来最新的requests库V2.13.0是支持https请求的,但是一般写脚本时候,我们会用抓包工具fiddler,这时候会 报:requests.exceptions.SSLError: [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed (_ssl.c:590) 小编…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
