自注意力简介
在注意力机制中,每个查询都会关注所有的键值对并生成一个注意力输出。如果查询q,键k和值v都来自于同一组输入,那么这个注意力就被称为是自注意力(self-attention)。自注意力这部分理论,我觉得台大李宏毅老师的课程讲得最好。

自注意力就是输入一堆向量,假设称为a1,a2,a3,a4,那么这四个向量都会参与自注意力机制的运算,得到的结果仍然是四个输出,这四个输出再去做全连接运算。而每一个自注意力机制的输出都用到了a1~a4四个向量来进行运算,也就是说每个输出都是观察了所有的输入之后才得到的。
首先,输入a1需要和a2,a3,a4分别计算相关性,这个相关性可以由缩放点积方式来计算,也就称作缩放点积注意力,也可以由两个两个输入向量相加后再做非线性处理得到,称为加性注意力。

缩放点积的计算方法如下:

输入一个向量v1和一个向量v2,v1去乘上一个可训练矩阵Wq得到q,v2去乘上一个可训练矩阵Wk得到k,再把这个q和k做一个点积运算,得到的就是α,类似于相似度。
回到前面的例子中,a1这里既作为q,又作为k,又作为v。其中,Wq*a1就是q1,Wk*a1就是k1,q1和k1的点积就是α11,相当于a1自己和自己的相似度,同样的,a1和a2,a3,a4分别计算得到α12,α13,α14,然后将α11,α12,α13,α14经过softmax得到最终的四个输出,如下图所示:

然后再用一个可训练矩阵Wv去乘以a1得到v1,用计算得到的相似度α'11去乘以v1,得到一个值temp11;同样的,用可训练矩阵Wv去乘以a2得到v2,用计算得到的相似度α‘12去乘以v2,得到temp12;类似的得到temp13,temp14,然后把temp11+temp12+temp13+temp14得到b1,这个b1就是自注意力机制的第一个输出。

我们刚刚是以a1的视角做的运算,得到b1,同样可以以a2,a3,a4的视角做运算,得到b2,b3,b4。这次就得到了自注意力机制的输出。光看最后这个结构图,有点类似全连接,只是里面的运算过程比全连接要复杂。

下面,我们来看一下如何用代码实现自注意力的计算。
import torch
import torch.nn as nn
import torch.nn.functional as F class SelfAttention(nn.Module):# embed_size代表输入的向量维度,heads代表多头注意力机制中的头数量def __init__(self, embed_size, heads): super(SelfAttention,self).__init__()self.embed_size = embed_sizeself.heads = headsself.head_dim = embed_size // heads # 每个头的维度# 用assert断言机制判断assert (self.head_dim * heads == embed_size), "Embedding size needs to be divisible by heads" # 没有偏置项,其实这个线性层本质上就是为了计算值Wv*a = Vself.values = nn.Linear(self.head_dim, self.head_dim, bias=False)self.keys = nn.Linear(self.head_dim, self.head_dim, bias=False)self.queries = nn.Linear(self.head_dim, self.head_dim, bias=False)# 最后的全连接操作,输出仍是输入的向量维度,也就是说大小是不变的self.fc_out = nn.Linear(heads*self.head_dim, self.embed_size)def forward(self, values, keys, query, mask):# 这个mask也很关键,它用于控制模型在处理序列数据时应该关注哪些部分,以及忽略哪些部分N = query.shape[0] # 获取输入的批量个数print("N:",N)value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1] # 获取输入序列的长度# Split the embedding into self.heads different pieces # 把k,q,v都切分为多个组values = values.reshape(N, value_len, self.heads, self.head_dim)keys = keys.reshape(N, key_len, self.heads, self.head_dim)queries = query.reshape(N, query_len, self.heads, self.head_dim)# 计算k,q,vvalues = self.values(values)keys = self.keys(keys)queries = self.queries(queries)energy = torch.einsum("nqhd,nkhd->nhqk",[queries, keys]) # 格式转化print("queries.shape:", queries.shape)print("keys.shape:", keys.shape)print("energy.shape:", energy.shape)if mask is not None:energy = energy.masked_fill(mask==0, float("-1e20"))attention = torch.softmax(energy/(self.embed_size**(1/2)), dim=3) # softmax内部是缩放点积print("attention.shape:", attention.shape)print("values.shape:", values.shape)out = torch.einsum("nhql,nlhd->nqhd", [attention, values]).reshape(N, query_len, self.heads*self.head_dim)out = self.fc_out(out)return outembed_size = 512
heads = 8
attention = SelfAttention(embed_size, heads)# batch size 1, seq length 60
values = torch.rand(1,60,embed_size)
keys = torch.rand(1,60,embed_size)
queries = torch.rand(1,60,embed_size)
mask = None # 假设没有maskout = attention(values, keys, queries, mask)
print(out.shape)# 输出
N: 1
queries.shape: torch.Size([1, 60, 8, 64])
keys.shape: torch.Size([1, 60, 8, 64])
energy.shape: torch.Size([1, 8, 60, 60])
attention.shape: torch.Size([1, 8, 60, 60])
values.shape: torch.Size([1, 60, 8, 64])
torch.Size([1, 60, 512])通过这个程序,我们可以看到,自注意力机制是不改变输入和输出的形状的,输入的Q,K,V格式是[1,60,512],输出的结果的仍然是[1,60,512]。
下面是几点说明:
1. 这里的embed_size代表的是输入到自注意力层中的每个元素的向量维度。在Transformer模型中,输入数据首先会被转换成一个固定长度的向量,这个向量的长度就称为embed_size。
2. mask表示的是模型在处理序列数据时,应该忽略掉哪部分,我这里设置为None,也就是全部参与计算。
3. einsum,称为爱因斯坦求和,起源是爱因斯坦在研究广义相对论时,需要处理大量求和运算,为了简化这种繁复的运算,提出了求和约定,推动了张量分析的发展。einsum 可以计算向量、矩阵、张量运算,如果利用得当,sinsum可完全代替其他的矩阵计算方法。
例如,C = einsum('ij,jk->ik', A, B),就相当于两个矩阵求内积:cik = Σj AijBjk。
通过输出可以看到,在计算前queries的形状是[1,60,8,64],keys的形状是[1,60,8,64],在表达式"nqhd,nkhd->nhqk"中,n=1,q=60,h=8,d=64,k=60,两个矩阵进行内积,因此得到的结果是nhqk,也就是[1,8,60,60]。
相关文章:

自注意力简介
在注意力机制中,每个查询都会关注所有的键值对并生成一个注意力输出。如果查询q,键k和值v都来自于同一组输入,那么这个注意力就被称为是自注意力(self-attention)。自注意力这部分理论,我觉得台大李宏毅老师…...

【GameFramework框架】7-2、GameFramework框架是否“过度设计”?
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 【GameFramework框架】系列教程目录: https://blog.csdn.net/q764424567/article/details/1…...
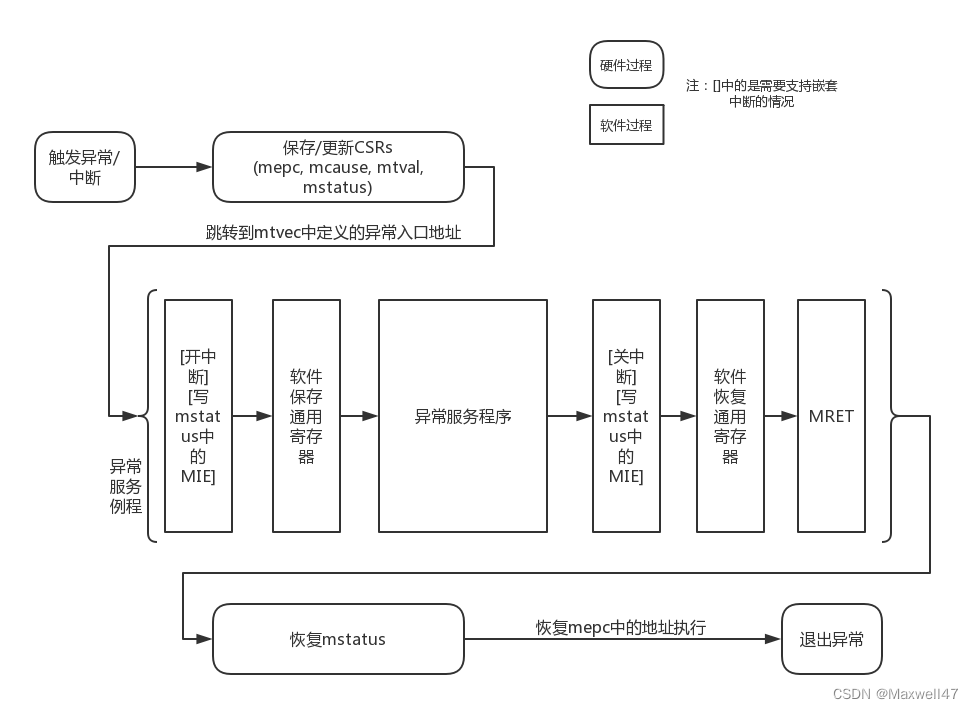
RISC-V异常处理流程概述(2):异常处理机制
RISC-V异常处理流程概述(2):异常处理机制 一、异常处理流程和异常委托1.1 异常处理流程1.2 异常委托二、RISC-V异常处理中软件相关内容2.1 异常处理准备工作2.2 异常处理函数2.3 Opensbi系统调用的注册一、异常处理流程和异常委托 1.1 异常处理流程 发生异常时,首先需要执…...

Unity3D中如何降低游戏的Drawcall详解
在Unity3D游戏开发中,Drawcall是一个至关重要的性能指标,它指的是CPU通知GPU绘制一个物体的命令次数。过多的Drawcall会导致游戏性能下降,因此优化Drawcall的数量是提高游戏性能的关键。本文将详细介绍Unity3D中降低Drawcall的几种主要方法&a…...

小程序-设置环境变量
在实际开发中,不同的开发环境,调用的接口地址是不一样的 例如:开发环境需要调用开发版的接口地址,生产环境需要正式版的接口地址 这时候,我们就可以使用小程序提供了 wx.getAccountInfoSync() 接口,用来获取…...

【RabbitMQ】一文详解消息可靠性
目录: 1.前言 2.生产者 3.数据持久化 4.消费者 5.死信队列 1.前言 RabbitMQ 是一款高性能、高可靠性的消息中间件,广泛应用于分布式系统中。它允许系统中的各个模块进行异步通信,提供了高度的灵活性和可伸缩性。然而,这种通…...

RuntimeError: Unexpected error from cudaGetDeviceCount
RuntimeError: Unexpected error from cudaGetDeviceCount 0. 引言1. 临时解决方法 0. 引言 使用 vllm-0.4.2 部署时,多卡正常运行。升级到 vllm-0.5.1 时,报错如下: (VllmWorkerProcess pid30692) WARNING 07-12 08:16:22 utils.py:562] U…...
基础认知)
uboot学习:(一)基础认知
目录 uboot是一个裸机程序(bootloader) 作用 要运行linux系统时,如何从外置的flash拷贝到DDR中,才能启动 uboot使用步骤 步骤1中的命令例子 注意 uboot源码获取方法 uboot是一个裸机程序(bootloader)…...
- 总体方差)
每天一个数据分析题(四百二十六)- 总体方差
为了比较两个总体方差,我们通常检验两个总体的() A. 方差差 B. 方差比 C. 方差乘积 D. 方差和 数据分析认证考试介绍:点击进入 题目来源于CDA模拟题库 点击此处获取答案 数据分析专项练习题库 内容涵盖Python,SQL,统计学&a…...

【C++】设计一套基于C++与C#的视频播放软件
在开发一款集视频播放与丰富交互功能于一体的软件时,结合C的高性能与C#在界面开发上的便捷性,是一个高效且实用的选择。以下,我们将概述这样一个系统的架构设计、关键技术点以及各功能模块的详细实现思路。 一、系统架构设计 1. 架构概览 …...

数学建模中的辅助变量、中间变量、指示变量
在数学建模中,除了决策变量外,还有一些其他类型的变量,如中间变量、辅助变量和指示变量。每种变量在模型中都有特定的用途和意义。以下是对这些变量的详细解释: 1. 决策变量(Decision Variables) 定义&am…...
和tell())
python的seek()和tell()
seek() seek() 是用来在文件中移动指针位置的方法。它的作用是将文件内部的当前位置设置为指定的位置。 seek(offset, whence) 参数说明 offset: 这是一个整数值,表示相对于起始位置的偏移量。如果是正数,表示向文件末尾方向移动;如果是负…...

Go泛型详解
引子 如果我们要写一个函数分别比较2个整数和浮点数的大小,我们就要写2个函数。如下: func Min(x, y float64) float64 {if x < y {return x}return y }func MinInt(x, y int) int {if x < y {return x}return y }2个函数,除了数据类…...

【每日一练】python之sum()求和函数实例讲解
在Python中, sum()是一个内置函数,用于计算可迭代对象(如列表、元组等)中所有元素的总和。如下实例: """ 收入支出统计小程序 知识点:用户输入获取列表元素添加sum()函数,统计作用 "&…...

打造智慧校园德育管理,提升学生操行基础分
智慧校园的德育管理系统内嵌的操行基础分功能,是对学生日常行为规范和道德素养进行量化评估的一个创新实践。该功能通过将抽象的道德品质转化为具体可量化的指标,如遵守纪律、尊师重道、团结协作、爱护环境及参与集体活动的积极性等,为每个学…...

自定义函数---随机数系列函数
大家有没有发现平常在写随机数的时候,需要引入很多的头文件,然后还需要用一些复杂的函数,大家可能不太习惯,于是我就制作了一个头文件 // random_number.h #ifndef RANDOM_NUMBER_H // 预处理指令,防止头文件被重复包含…...
一文了解5G新通话技术演进与业务模型
5G新通话简介 5G新通话,也被称为VoNR,是基于R16及后续协议产生的一种增强型语音通话业务。 它在IMS网络里新增数据通道(Data Channel),承载通话时的文本、图片、涂鸦、菜单等信息。它能在传统话音业务基础上提供更多服…...

视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器
视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器。 视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器 同三…...

el-input-number计数器change事件校验数据,改变绑定数据值后change方法失效问题的原因及解决方法
在change事件中如果对el-input-number绑定的数据进行更改,会出现change事件失效的问题 试过:this.$set()及赋值等方法,都无法解决 解决方法:用$nextTick函数对绑定值进行更改( this.$nextTick(() > { this.绑定…...

将vue项目整合到springboot项目中并在阿里云上运行
第一步,使用springboot中的thymeleaf模板引擎 导入依赖 <!-- thymeleaf 模板 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency> 在r…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
