【数据结构】堆和集合笔记
自己写一个堆
首先,明确一下,为什么需要堆?
=>考虑插入,删除,查找的效率。
数组,查找,最快是二分查找O(lgN)。但查找完如果要做什么操作,比如删除,就要挪动元素了。所以合起来效率是O(lgN)+O(N)=O(N)
二叉树,看起来是O(lgN),但之前写树的时候有说过,链表是不是树?是树的退化形态,每个结点都有小于等于一个的儿子。这个时候查找的效率是O(lgN)了。之前说,查找之后万一要做什么操作,树就可能不是完全二叉树,即查找效率为O(lgN)。
能不能试图用平衡二叉树?不能,rotate非常麻烦。
=>所以尝试保持一颗完全二叉树=>给这棵树起名堆。
接下来考虑需要用什么基础的数据结构存储。
需要指针吗?
完全二叉树是每一个结点要么没有儿子,要么有两个儿子,在堆里只有最后一个有儿子的父节点可以只有左儿子。所以完全可以用数组表示。
假如链表下标从1开始,2和3是它的子节点,2/2=1,3/2=1,父节点访问也很方便。
初始化
表示这棵树需要几个数据:总容量,现在有多少元素,以及存放元素的数组。
初始化需要提供总容量。
插入元素
为确保是一个完全二叉树,插在最后。
堆需要确保一件事情,小元素在上,大元素在下。所以需要向上进行一次数据交换,寻找插入值的最终位置。
注意,这里说的是寻找,不需要真的交换,只需要挪动不符合要求的元素,找到插入值的最终位置赋值即可。
删除元素
删除一定是删最小的。其余和插入一样。
为确保是一个完全二叉树,将最后一个元素和被删除的第一个元素交换,然后向下寻找最终位置。
4. 一个数组的插入
为了保证堆的性质,插入数组后需要排序。
思考一下,哪些需要排序?
如果向下调整位置,则叶子结点不需要轮。如果向上调整位置,则根节点不需要轮。
效率为重,叶子结点最多,如果向上调整,则叶子结点需要轮的距离最远。而事实上,叶子结点又占了树结点的很大一部分。
所以我们选择向下调整。
完整代码(包括测试)
#include<iostream>
using namespace std;
class h{
private:int *nums;int capacity;int l;
public:h(){capacity=0;}void init(int c=1){capacity=c;l=0;nums=new int [c+1];}void printh(){for(int i=1;i<=l;i++){cout<<nums[i]<<" ";}cout<<endl;}int isfull(){if(capacity==l){return 1;}return 0;}void moveup(int k){int tempnum=nums[k];int i=k;for(i;tempnum<nums[i/2]&&i>1;i/=2){nums[i]=nums[i/2];}nums[i]=tempnum;}int insert(int n){if(isfull()){return 0;}nums[l+1]=n;l++;moveup(l);return 1;}int isempty(){if(l==0){return 1;}return 0;}void movedown(int k){int tempnum=nums[k];int i=k;while(i*2<=l){int child=i*2;if(child<l){if(nums[child]>nums[child+1]){child++;}}if(nums[child]<tempnum){nums[i]=nums[child];i=child;}else{nums[i]=tempnum;return ;}}nums[i]=tempnum;return ;}int remove(){if(isempty()){return 0;}nums[1]=nums[l];l--;movedown(1);return 1;}void buildheap(int *a,int len,int c=0){if(len>c){c=len;}init(c);l=len;for(int i=0;i<len;i++){nums[i+1]=a[i];}for(int i=len/2;i>=1;i--){movedown(i);}}
};
int main(){int a[6]={10,50,60,5,30,20};h h1;h1.buildheap(a,6);h1.printh();
}2. c++的堆
堆在queue中,叫priority_queue,默认是大顶堆,即树根是最大的元素,可以执行一下验证。
所以插入是push,查看堆顶元素是top(),弹出堆顶是pop()。
#include<iostream>
#include<queue>
using namespace std;
int main(){priority_queue<int>q1;int a[6]={111,222,333,11,22};for(int i=0;i<5;i++){q1.push(a[i]);}cout<<q1.top()<<endl;q1.pop();cout<<q1.top()<<endl;
}堆额外有一种方法让其变为小顶堆,即提供一个容器,前提是这个容器支持从小到大排序,比如vector。
可以借助以下程序验证。
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int main(){priority_queue<int,vector<int>,greater<int> >q1;int a[5]={111,222,333,11,22};for(int i=0;i<5;i++){q1.push(a[i]);}for(int i=0;i<5;i++){cout<<q1.top()<<endl;q1.pop();}
}3. c++的集合
集合就是set嘛,之前刷题用了好多次了。
注意三点:
set默认从小到大排序(因为底层实现是红黑树,类似AVL树)
set.insert()也可以插入集合,方法详见下方实验代码
对于力扣中要求返回vector但你用set做了,只要返回{set.begin(), set.end()}即可
可以用以下代码验证set
#include<iostream>
#include<set>
using namespace std;
int main(){set<int>s1;int a1[3]={333,222,111};for(int i=0;i<3;i++){s1.insert(a1[i]);}for(auto x:s1){cout<<x<<" ";}cout<<endl;set<int>s2;s2.insert(666);s2.insert(555);s1.insert(s2.begin(),s2.end());for(auto x:s1){cout<<x<<" ";}cout<<endl;
}相关文章:

【数据结构】堆和集合笔记
自己写一个堆首先,明确一下,为什么需要堆?>考虑插入,删除,查找的效率。数组,查找,最快是二分查找O(lgN)。但查找完如果要做什么操作,比如删除,就要挪动元素了。所以合…...
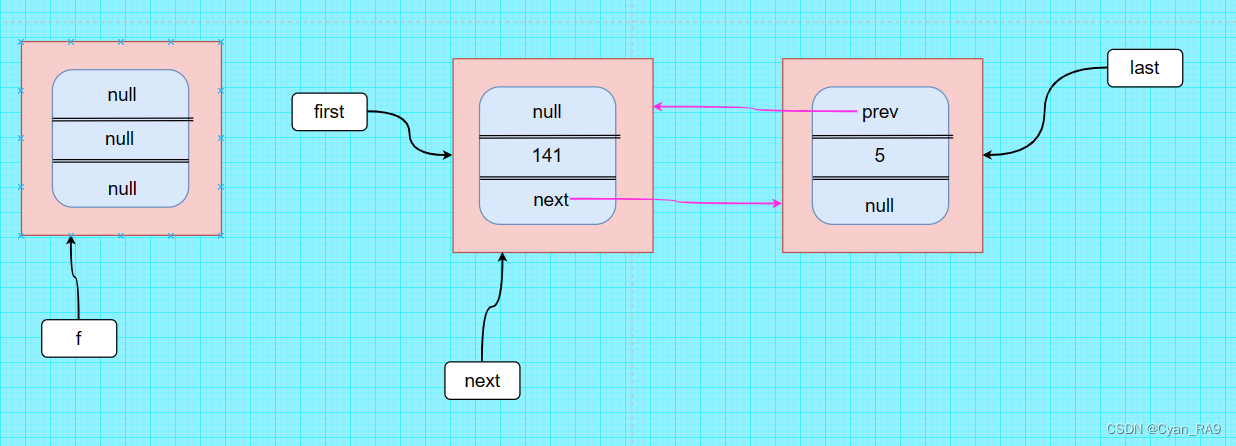
java LinkedList 源码分析(通俗易懂)
目录 一、前言 二、LinkedList类简介 三、LinkedList类的底层实现 四、LinkedList类的源码解读 1.add方法解读 : 〇准备工作 。 ①跳入无参构造。 ②跳入add方法。 ③跳入linkList方法。 ④增加第一个元素成功。 ⑤向链表中添加第二个元素。 2.remove方法解读 : 〇准备工…...

Vue中实现路由跳转的三种方式详细分解
vue中实现路由跳转的三种方式 目录 vue中实现路由跳转的三种方式 一、使用vue-router 1.下载vue-router模块到当前工程 2.在main.js中引入VueRouter函数 3.添加到Vue.use()身上 – 注册全局RouterLink和RouterView组件 4.创建路由规则数组 – 路径和组件名对应关系 5…...

全国自学考试03708《中国近现代史纲要》重点复习精要
1. 西方列强的殖民扩张和鸦片战争的影响。(两面性) :反面—破坏了了中国的小农经济,是中国由封建社会转变为两半社会。 --一系列不公平条约,破坏了中国主权领土完整。 --压迫中国人民,给中国人民带来了巨大…...

数据库面试题——锁
了解数据库的锁吗? 锁是数据库系统区别于文件系统的一个关键特性,锁机制用于管理对共享资源的并发访问。 InnoDB下两种标准行级锁: 共享锁(S Lock),允许事务读一行数据。 排他锁(X Lock&…...

Python笔记 -- 文件和异常
文章目录1、文件1.1、with关键字1.2、逐行读取1.3、写入模式1.4、多行写入2、异常2.1、try-except-else2.2、pass1、文件 1.1、with关键字 with关键字用于自动管理资源 使用with可以让python在合适的时候释放资源 python会将文本解读为字符串 # -*- encoding:utf-8 -*- # 如…...

蓝桥杯刷题冲刺 | 倒计时24天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.修剪灌木2.统计子矩阵1.修剪灌木 题目 链接: 修剪灌木 - 蓝桥云课 (lanqiao.cn) 找…...
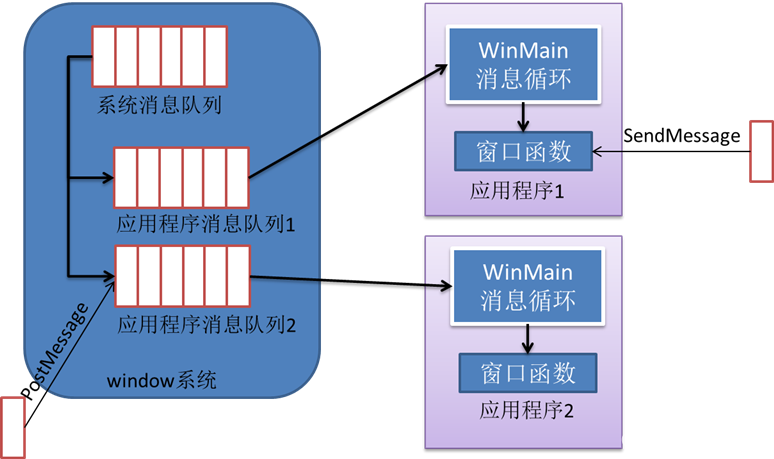
真正理解微软Windows程序运行机制——什么是消息
我是荔园微风,作为一名在IT界整整25年的老兵,今天说说Windows程序的运行机制。经常被问到MFC到底是一个什么技术,为了解释这个我之前还写过帖子,但是很多人还是不理解。其实这没什么,我在学生时代也被这个问题困绕过。…...
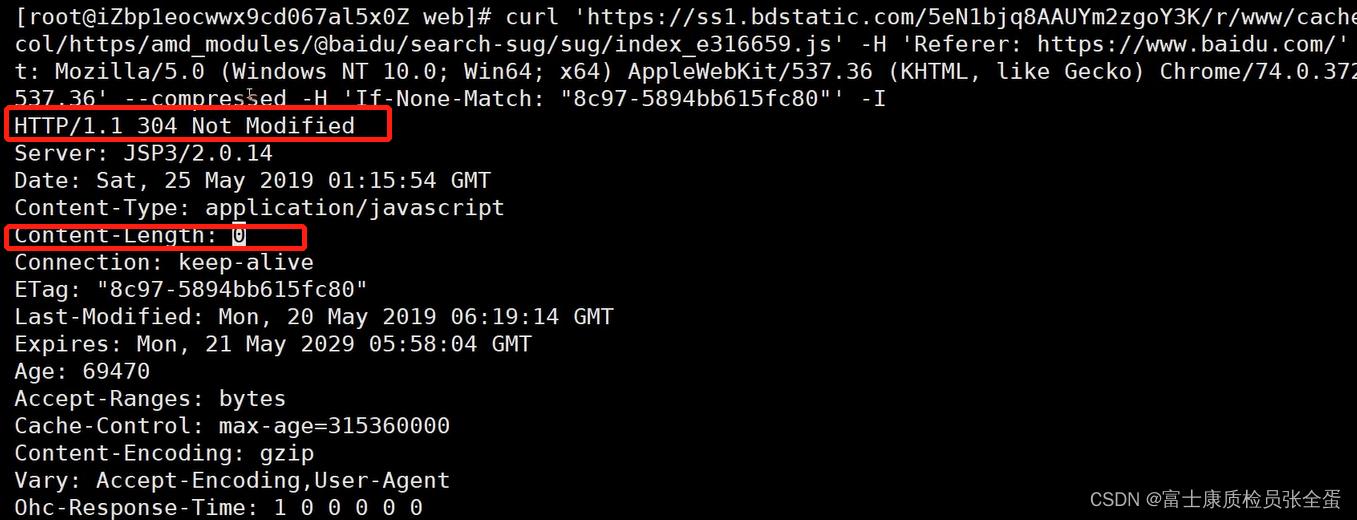
HTTP 缓存的工作原理
缓存是解决http1.1当中的性能问题主要手段。缓存可能存在于客户端浏览器上,也可以存在服务器上面,当使用过期缓存可能给用户展示的是错误的信息而导致一些bug。 HTTP 缓存:为当前请求复用前请求的响应 • 目标:减少时延࿱…...
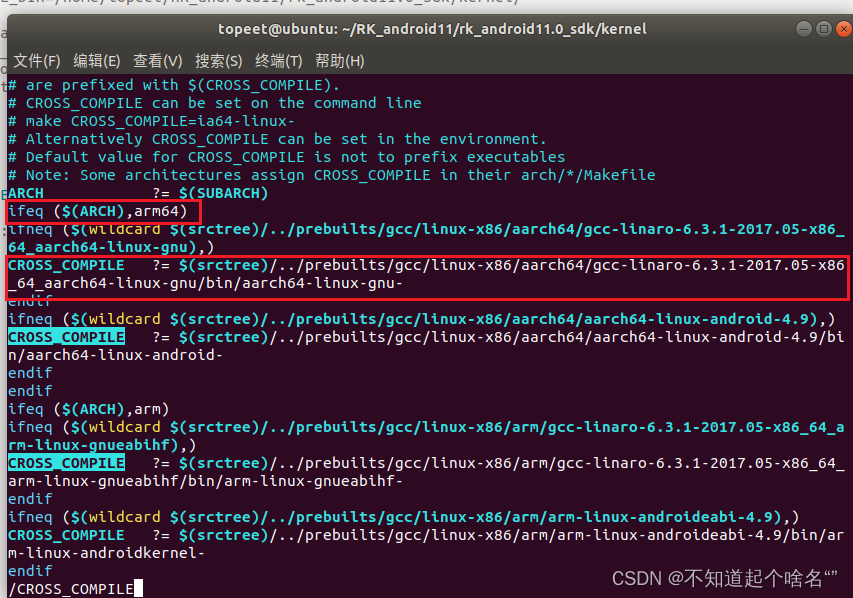
RK3568在Android上进行驱动模块开发(源码外)
文章目录 前言一、ARCH架构二、编译器三、建立自己的Makefile文件总结前言 本文记录在驱动开发时,由于编译内核时间较长,经常会选择单独编译一个模块,这里主要讲解,makefile文件如何编写(主要是编译器和架构) 提示:以下是本篇文章正文内容,下面案例可供参考 一、ARCH…...

操作技巧 | 在Revit中借用CAD填充图案的方法
在建模过程中,有时需要达到多种填充效果,而CAD中大量的二维填充图案,便是最直接的资源之一。 使用 填充图案之前 使用 填充图案之后 其中要用到主要命令便是对表面填充图案的添加与编辑 简单效果 如下 模型填充与绘图填充 区别 模型填…...
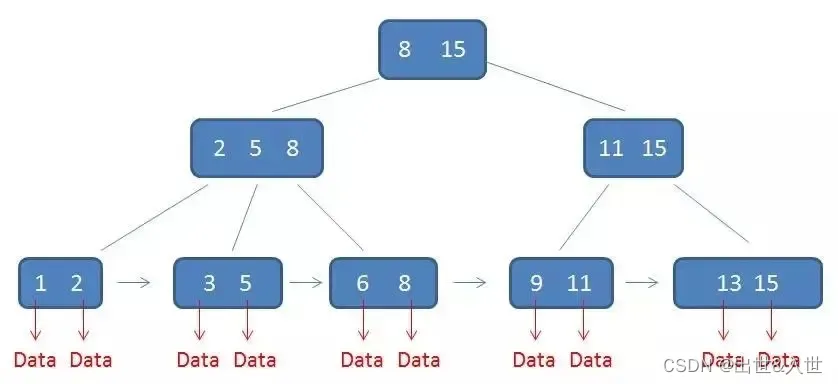
Java的二叉树、红黑树、B+树
数组和链表是常用的数据结构,数组虽然查找快(有序数组可以通过二分法查找),但是插入和删除是比较慢的;而链表,插入和删除很快(只需要改变一些引用值),但是查找就很慢&…...

昨天某读者拿到华为OD岗位offer,今天来分享一下经验,包含华为OD机试
来自读者投稿,已经拿到华为 OD 开发岗位 offer,询问了一些问题,下面是他的一些经验。 文章目录华为 OD 投递简历华为 OD 机试分数OD 机试通过之后,收到综合测评OD 技术面(时长 1 小时左右)主管/HR 面试&…...
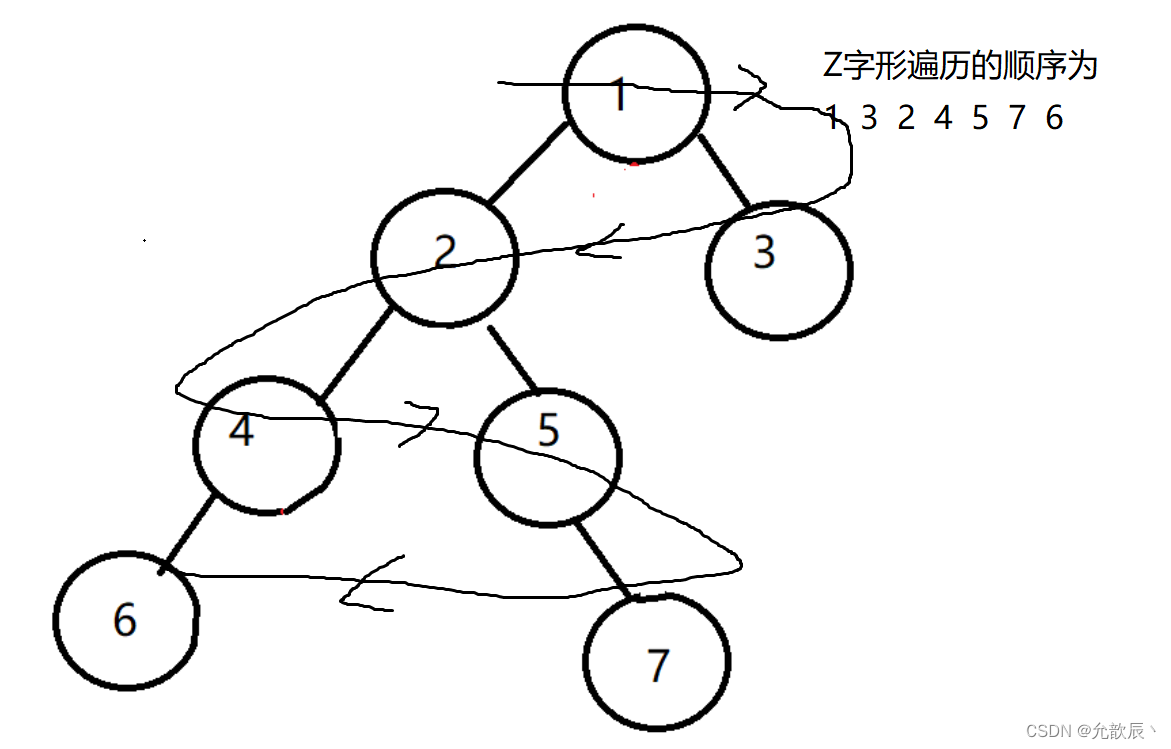
树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
目录 一.前序遍历 1.递归 2.栈迭代 3.Morris遍历 二.中序遍历 1.递归 2.栈迭代 3.Morris遍历 三.后序遍历 1.递归 2.栈迭代 3.Morris遍历 四.前中后序的统一迭代法 1.前序遍历 2.中序遍历 3.后序遍历 五.层序遍历 1.队列迭代 2.之字形层序遍历 3.锯齿形层序…...
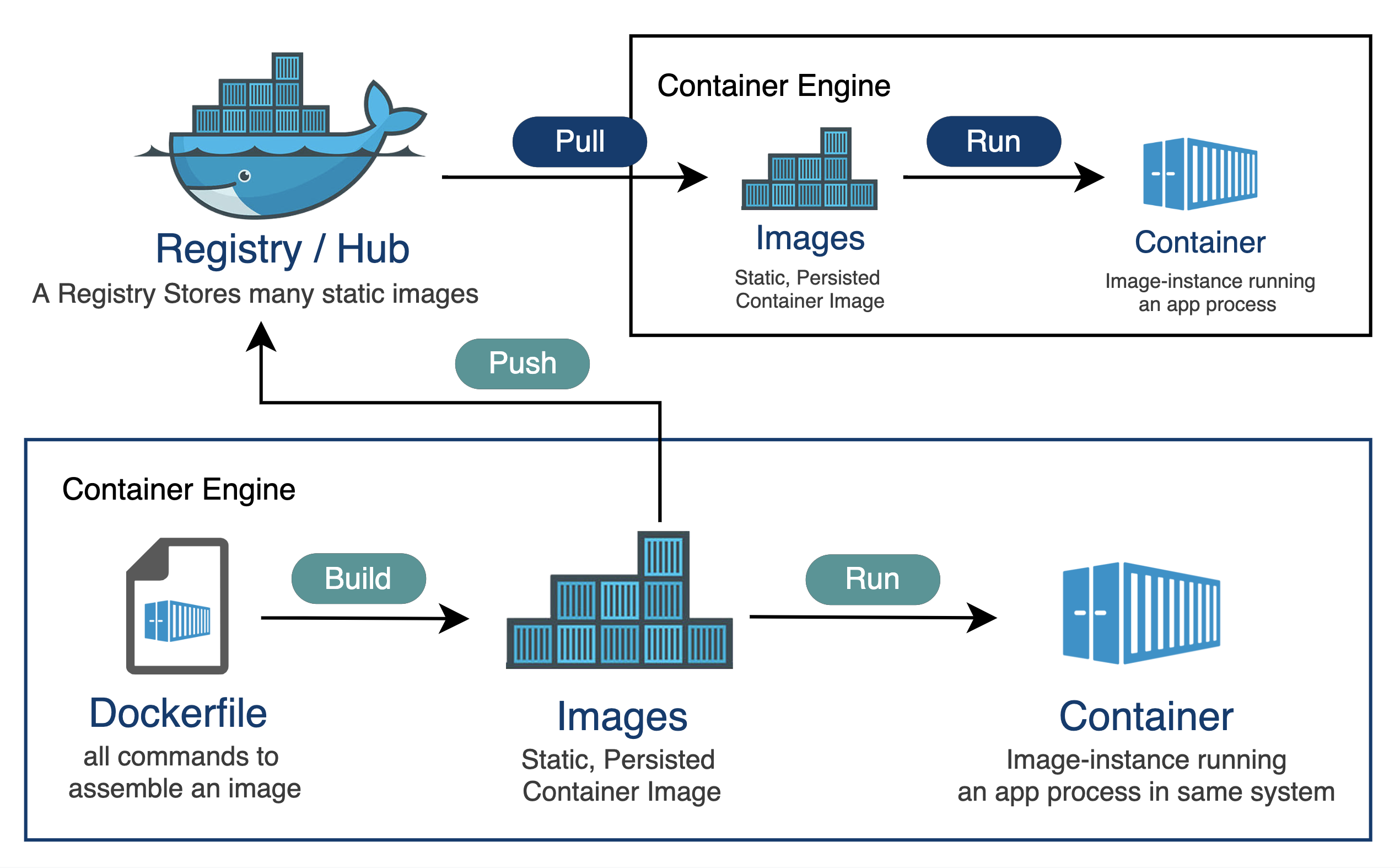
Docker Registry部署镜像私有仓库及鉴权认证
文章目录一、Docker Registry是什么?二、Docker Registry部署私有仓库2.1、Docker Registry安装2.2、Docker Registry配置2.3、启动Docker Registry2.4、Docker客户端配置2.5、向Docker Registry上传和下载镜像三、Docker Registry鉴权和认证3.1、基本认证3.2、Bear…...
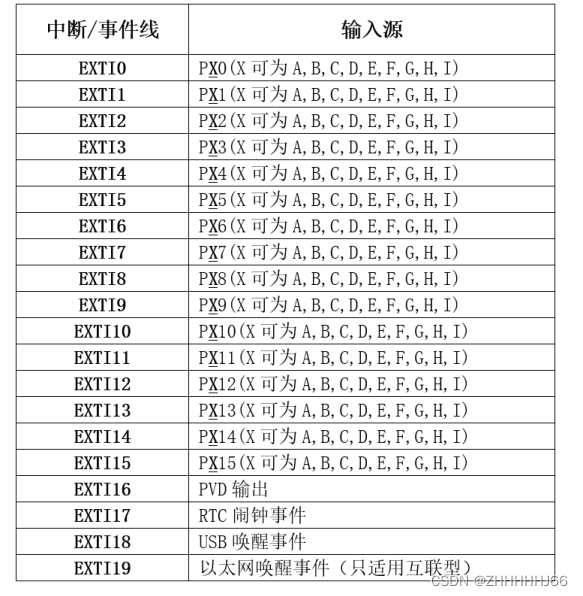
stm32外设-中断详解
0. 写在最前 本栏目笔记都是基于stm32F10x 1. 中断是啥? 什么是中断:CPU在处理某一事件A时,发生的另外某一事件B请求CPU去处理(产生了中断),随后CPU暂时中断当前正在执行的任务,去对事件B进行处…...
第十四届蓝桥杯三月真题刷题训练——第 13 天
目录 第 1 题:特殊日期 问题描述 答案提交 运行限制 代码: 思路: 第 2 题:重合次数 问题描述 答案提交 运行限制 代码: 第 3 题:左移右移 问题描述 输入格式 输出格式 样例输入 样例输出…...

webgl_gpgpu_birds 样例分析
webgl_gpgpu_birds 是一个 three.js 的官方样例,这个例子模拟了鸟群的运动,是一个群组动画,并且动画的帧率也很高;鸟群的运动很自然,非常值得研究。类似的群组动画还有鱼群,boid是‘类鸟群’的英文 大概两…...

以业务行为驱动的反入侵安全能力建设
0x0 背景 最近听到一些甲方安全领域的专家分享了部分安全建设的经验,对安全运营下的反入侵技术能力建设有了些新的看法,依靠单个/多个异构的安全产品的关联能力形成的安全中台并不能在实际的攻防对抗当中占据主动地位,且很容易达到一个天花板…...

Unity3d C#使用DOTween插件的Sequence实现系列动画OnComplete无效和颜色设置无效的问题记录
前言 最近在弄一个文字动画效果的动画,使用了DOTween插件的Sequence来实现,主要就是对一个Text进行的文字打字、缩放和颜色设置等动画,功能是先对Text实现打字的动画,打字完成后,延时几秒对文字进行缩小、颜色变淡&am…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
