Java的二叉树、红黑树、B+树
数组和链表是常用的数据结构,数组虽然查找快(有序数组可以通过二分法查找),但是插入和删除是比较慢的;而链表,插入和删除很快(只需要改变一些引用值),但是查找就很慢,需要从头开始遍历;
那么有没有一种数据结构能同时具备数组查找快的优点以及链表插入和删除快的优点呢,那就是接下来要介绍的——树。
1、二叉查找树
特性:
- 1、左子树上所有节点的值均小于它的根节点的值;
- 2、右子树上所有节点的值均大于它的根节点的值;
- 3、左、右子树也分别为二叉排序树。
但是一个不好会形成链表结构,比如一个有序数组形成的二叉树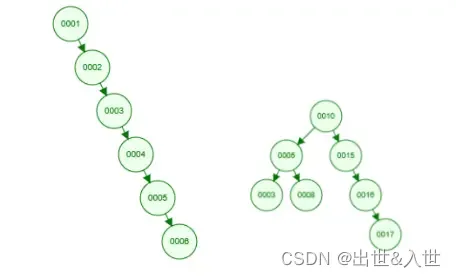
2、平衡二叉查找树
特性:
- 1、在二叉树的基础上,要求两个子树的高度差不能超过1;
- 2、每次增删都会通过一次或多次旋转来平衡二叉树;
调整平衡的基本思想:
当在二叉排序树中插入一个节点时,首先检查是否因插入而破坏了平衡,若破坏,则找出其中的最小不平衡二叉树,在保持二叉排序树特性的情况下,调整最小不平衡子树中节点之间的关系,以达到新的平衡。
所谓最小不平衡子树,指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树。
先插入指定节点,记录下当前节点的信息,LH,EH或者RH。
- 若左子树高LH,查看其左子树根节点的信息,若是LH,则一次右旋;若是RH,则一次左旋+一次右旋
- 若右子树高RH,查看右子树根节点的信息,若是RH,则一次左旋;若是LH,则一次右旋+一次左旋
- 调整改变的节点信息
虽然平衡树解决了二叉查找树退化为近似链表的缺点,能够把查找时间控制在 O(logn),不过却不是最佳的,因为平衡树要求每个节点的左子树和右子树的高度差至多等于1,这个要求实在是太严了,导致每次进行插入/删除节点的时候,几乎都会破坏平衡树的第二个规则,进而我们都需要通过左旋和右旋来进行调整,使之再次成为一颗符合要求的平衡树,且随着树的高度的增加,动态插入和删除的代价也越来越大,为了解决优化插入和删除性能,红黑树出现了。
显然,如果在那种插入、删除很频繁的场景中,平衡树需要频繁着进行调整,这会使平衡树的性能大打折扣,为了解决这个问题,于是有了红黑树,红黑树具有如下特点:
3、红黑树:
特性:
- 1、根节点是黑色;
- 2、每个节点或者是黑色,或者是红色;
- 3、每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!;
- 4、如果一个节点是红色的,则它的子节点必须是黑色的,也就是说一个红节点的父节点只能是黑色
- 5、从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点,也就是说确保没有一条路径会比其他路径长出俩倍;
红黑树(Red Black Tree) 是一种自平衡二叉查找树
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
二叉平衡树的严格平衡策略以牺牲建立查找结构(插入,删除操作)的代价,换来了稳定的O(logN) 的查找时间复杂度
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
红黑树的操作代价:
-
查找代价:由于红黑树的性质(最长路径长度不超过最短路径长度的2倍),可以说明红黑树虽然不像平衡二叉查找树一样是严格平衡的,但平衡性能还是要比二叉查找树要好。其查找代价基本维持在O(logN)左右,但在最差情况下(最长路径是最短路径的2倍少1),比平衡二叉查找树要略逊色一点。
-
插入代价:RBT插入结点时,需要旋转操作和变色操作。但由于只需要保证RBT基本平衡就可以了。因此插入结点最多只需要2次旋转,这一点和平衡二叉查找树的插入操作一样。虽然变色操作需要O(logN),但是变色操作十分简单,代价很小。
-
删除代价:红黑树的删除操作代价要比平衡二叉查找树要好的多,删除一个结点最多只需要3次旋转操作。
RBT 效率总结 : 查找效率最好情况下时间复杂度为O(logN),但在最坏情况下比平衡二叉查找树要差一些,但也远远好于二叉查找树。
插入和删除操作改变树的平衡性的概率要远远小于AVL(RBT不是高度平衡的)。因此需要的旋转操作的可能性要小,而且一旦需要旋转,插入一个结点最多只需要旋转2次,删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN),但是实际上,这种操作由于简单所需要的代价很小。
红黑树能够以O(log2(N))的时间复杂度进行搜索、插入、删除操作。此外,任何不平衡都会在3次旋转之内解决。这一点是平衡二叉查找树所不具备的。
调整平衡的基本思想:
- 变色:为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
- 左旋转:逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。说起来很怪异,大家看下图:
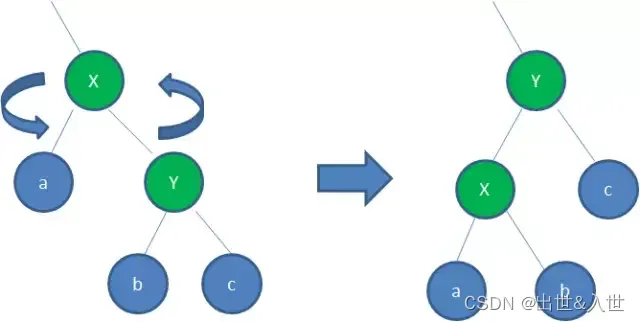
- 右旋转:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。大家看下图:
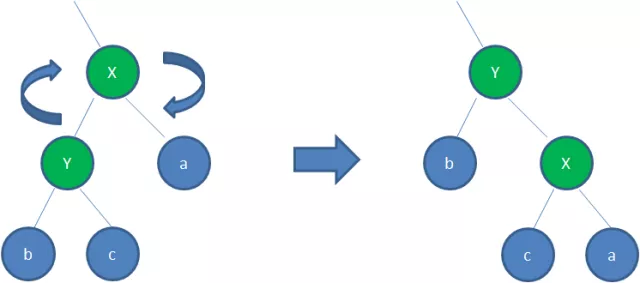
场景:HashMap TreeSet TreeMap
4、 B树:
设计缘由:
数据库索引是存储在磁盘上的,当数据量比较大的时候,索引的大小可能有十几个G,甚至更多。当我们利用索引查询的时候,能把整个索引全部加载到内存吗?显然不可能,能做的只有逐一加载每一个磁盘页,这里的磁盘页对应着索引树的节点。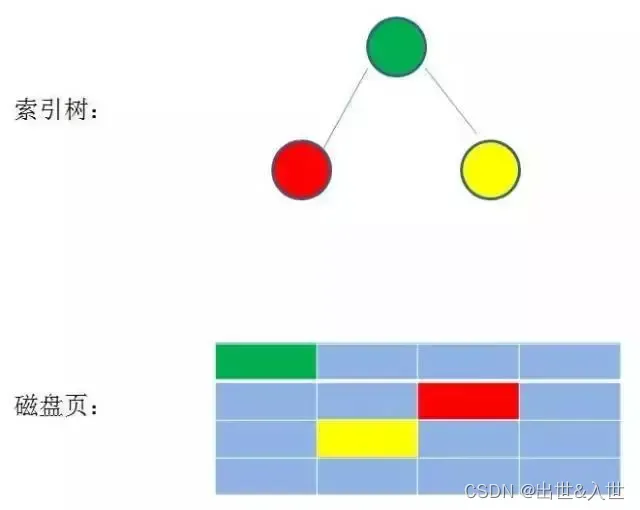
如果我们利用二叉查找树作为索引结构,那么最坏(每个节点数据在不同磁盘页上)的情况下,磁盘IO次数等于索引树的高度。 所以,为了减少磁盘IO次数,我们就需要把原本“瘦高”的树结构变得“矮胖”(节点数变少了)。这就是B树的特征之一
B树是一种多路平衡查找树,它的每一个节点最多包含m个孩子,m被称为B树的阶,m的大小取决于磁盘页的大小。——一个节点最多包含一个磁盘页的数据
也就是说,当B树变得矮胖以后,每个节点可以包含多个数据(数据量大小由磁盘页的大小决定),同样的数据,B树比二叉树/红黑树节点少。所以,B树在查询时,磁盘IO次数变少了,从而可以提升查找性能。
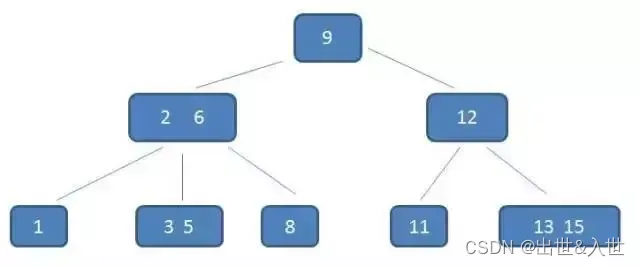
特征:
一个m阶的B树具有如下几个特征:
- 1.根结点至少有两个子女。
- 2.每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
- 3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
- 4.所有的叶子结点都位于同一层。
- 5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划
场景:
B树主要应用于文件系统以及部分数据库索引,比如著名的非关系型数据MongoDB。
而大部分关系型数据库,比如mysql,则使用B+树作为索引
5、 B+树
B+树是B树的一种变体,但是又有所不同,
特征:
一个m阶的B+树具有如下几个特征:
-
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
-
2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
-
3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
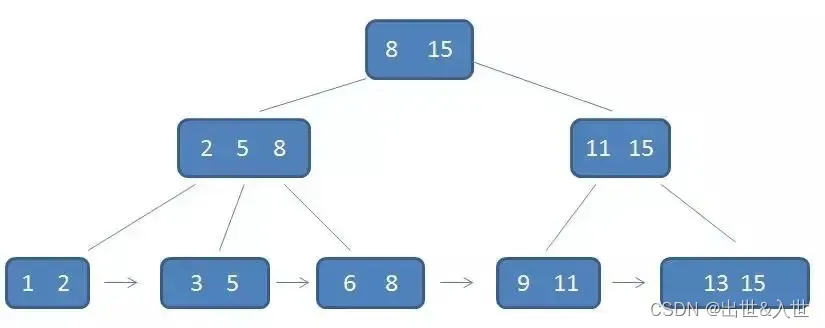
这里特别要注意有两点:
其一:每个父节点的元素都出现在子节点中,是子节点的最大(或最小)元素;因此所有叶子节点包含了全量元素信息;
其二:每个叶子节点都带有指向下一个节点的指针,形成了一个有序链表;
其三:只有叶子节点带有卫星数据,其余中间节点仅仅是索引,没有任何数据关联,如下图,所谓卫星数据,指的是索引元素所指向的数据记录,比如数据库中的某一行,在B树种,无论中间节点还是叶子节点都带有卫星数据。
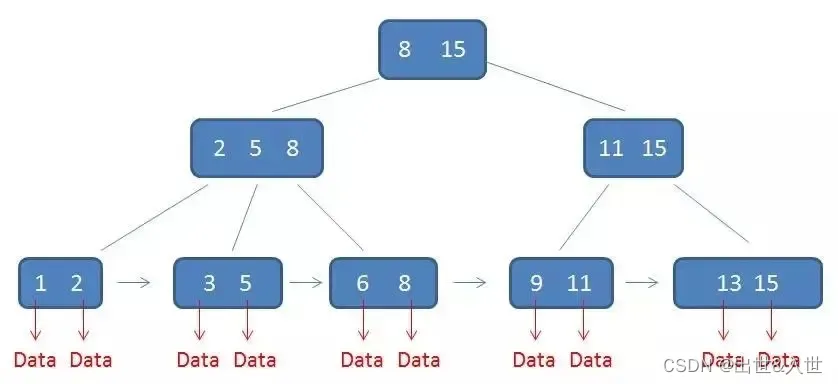
设计优势
B+树的好处主要体现在查询性能上,由于B+树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素,这就意味着,一次性加载到内存中的节点元素更多,从而使得查询时IO次数也更少。(举个简单的例子,一个磁盘页可以加载B树的100个节点元素,但是可以加载B+树的1000个节点元素,那么对于查找999这个数来说,B数需要10次IO,B+数只需要1次IO)
B+树相对B树的优点:
-
IO一次读数据是从磁盘上读的,磁盘容量是固定的,取数据量大小是固定的,非叶子节点不存储数据,节点小,磁盘IO次数就少。
-
B+树查询性能稳定,因为B+树的查询必须最终查找到叶子节点;
而B树,只要找到匹配元素即可,无论匹配元素处于中间节点,还是叶子节点。所以B树的查询性能并不稳定,最好情况是只查根节点,最坏情况是查到叶子节点 -
B+树的所有Data域在叶子节点,一般来说都会进行一个优化,就是将所有的叶子节点用指针串联起来(可以认为是链表),遍历叶子节点就能获取全部数据,这样就能进行区间访问了。
B树做范围查询,只能繁琐的遍历,但是B+树,只需要查到查找到范围下限以后,遍历叶子节点(有序链表)就可以了。
综合起来,B+树比B树的优势有三个:1、IO次数更少;2、查询性能更佳;3、范围查询简便
场景:Mysql索引
6、红黑树 VS B+树
红黑树的深度比B+树大,当数据量小时,可以把数据完全放到内存中,红黑树的时间复杂度比B树低(不用每次都查到叶子节点),如linux中进程的调度用的是红黑树,Java中HashMap、TreeMap、TreeSet(都在内存中操作)也都是用红黑树实现;
但是,当数据量大时,不能一次性把数据放到内存时,红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁,进而导致效率低下;而B树因其读磁盘次数少,具有更快的速度。
相关文章:

Java的二叉树、红黑树、B+树
数组和链表是常用的数据结构,数组虽然查找快(有序数组可以通过二分法查找),但是插入和删除是比较慢的;而链表,插入和删除很快(只需要改变一些引用值),但是查找就很慢&…...

昨天某读者拿到华为OD岗位offer,今天来分享一下经验,包含华为OD机试
来自读者投稿,已经拿到华为 OD 开发岗位 offer,询问了一些问题,下面是他的一些经验。 文章目录华为 OD 投递简历华为 OD 机试分数OD 机试通过之后,收到综合测评OD 技术面(时长 1 小时左右)主管/HR 面试&…...
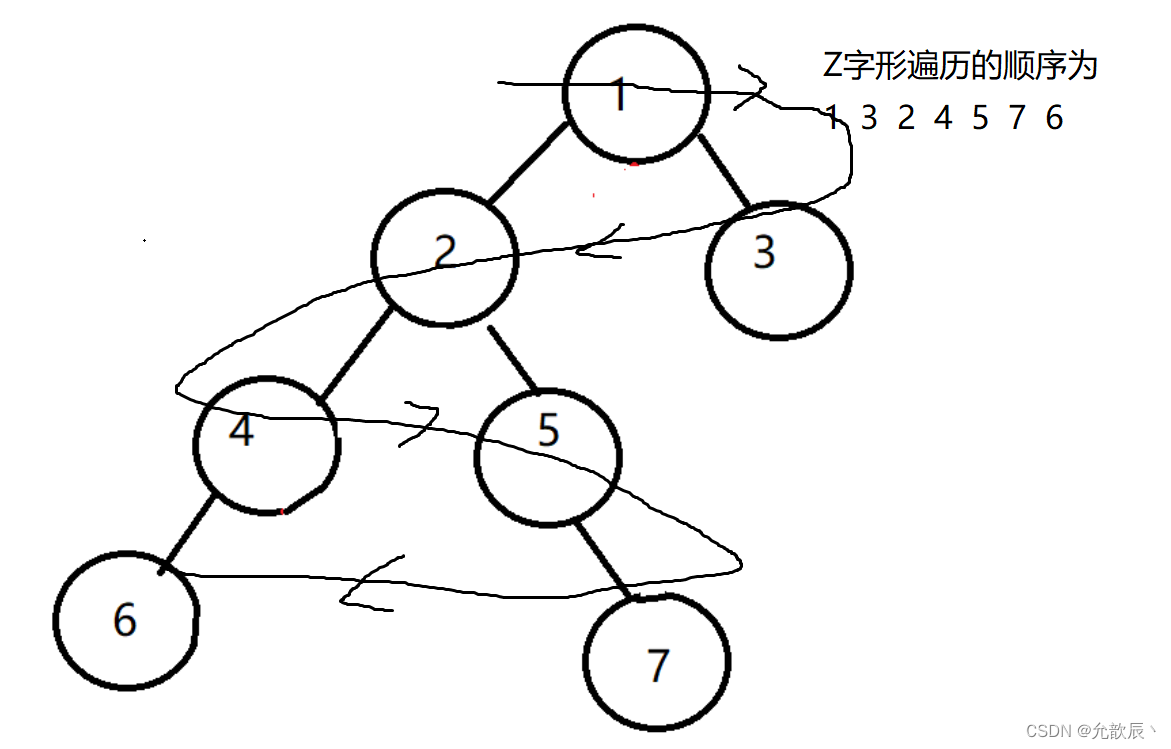
树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
目录 一.前序遍历 1.递归 2.栈迭代 3.Morris遍历 二.中序遍历 1.递归 2.栈迭代 3.Morris遍历 三.后序遍历 1.递归 2.栈迭代 3.Morris遍历 四.前中后序的统一迭代法 1.前序遍历 2.中序遍历 3.后序遍历 五.层序遍历 1.队列迭代 2.之字形层序遍历 3.锯齿形层序…...
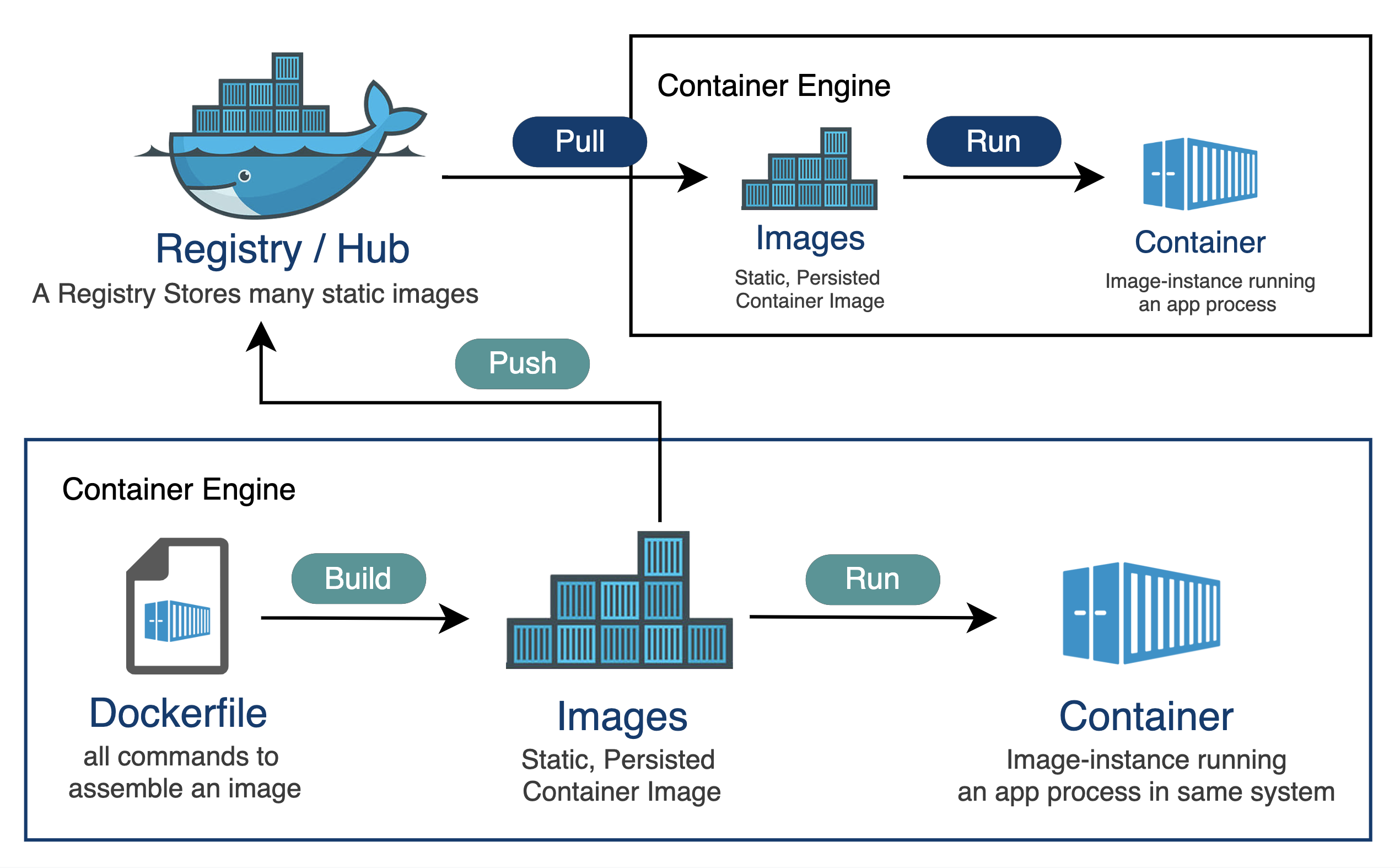
Docker Registry部署镜像私有仓库及鉴权认证
文章目录一、Docker Registry是什么?二、Docker Registry部署私有仓库2.1、Docker Registry安装2.2、Docker Registry配置2.3、启动Docker Registry2.4、Docker客户端配置2.5、向Docker Registry上传和下载镜像三、Docker Registry鉴权和认证3.1、基本认证3.2、Bear…...
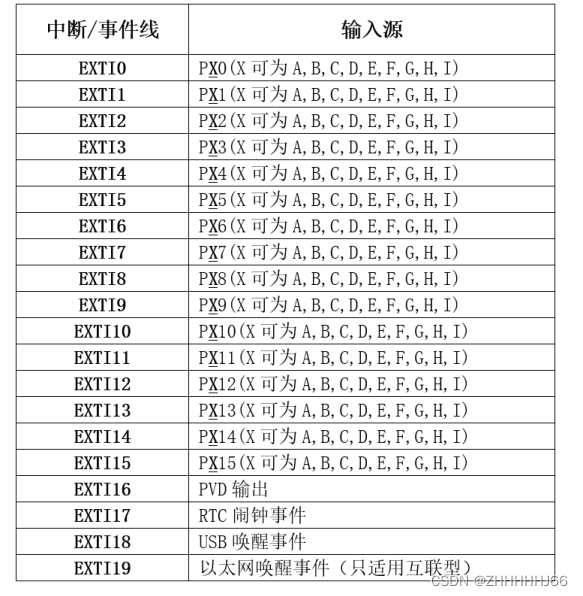
stm32外设-中断详解
0. 写在最前 本栏目笔记都是基于stm32F10x 1. 中断是啥? 什么是中断:CPU在处理某一事件A时,发生的另外某一事件B请求CPU去处理(产生了中断),随后CPU暂时中断当前正在执行的任务,去对事件B进行处…...
第十四届蓝桥杯三月真题刷题训练——第 13 天
目录 第 1 题:特殊日期 问题描述 答案提交 运行限制 代码: 思路: 第 2 题:重合次数 问题描述 答案提交 运行限制 代码: 第 3 题:左移右移 问题描述 输入格式 输出格式 样例输入 样例输出…...

webgl_gpgpu_birds 样例分析
webgl_gpgpu_birds 是一个 three.js 的官方样例,这个例子模拟了鸟群的运动,是一个群组动画,并且动画的帧率也很高;鸟群的运动很自然,非常值得研究。类似的群组动画还有鱼群,boid是‘类鸟群’的英文 大概两…...

以业务行为驱动的反入侵安全能力建设
0x0 背景 最近听到一些甲方安全领域的专家分享了部分安全建设的经验,对安全运营下的反入侵技术能力建设有了些新的看法,依靠单个/多个异构的安全产品的关联能力形成的安全中台并不能在实际的攻防对抗当中占据主动地位,且很容易达到一个天花板…...

Unity3d C#使用DOTween插件的Sequence实现系列动画OnComplete无效和颜色设置无效的问题记录
前言 最近在弄一个文字动画效果的动画,使用了DOTween插件的Sequence来实现,主要就是对一个Text进行的文字打字、缩放和颜色设置等动画,功能是先对Text实现打字的动画,打字完成后,延时几秒对文字进行缩小、颜色变淡&am…...

【蓝桥杯-筑基篇】排序算法
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 前言: 一、冒泡排序 二、选择排序 三、插入排序 四、图书推荐 前言: 算法工具推荐: 还在为数据结构发愁吗?这款可视化工具,帮助你更好的了解…...
编辑器进化 VSCode + Vim
本文作者为 360 奇舞团前端工程师VSCode 是一款非常流行的代码编辑器。它支持多种编程语言,拥有丰富的插件和调试功能,不论是处理前端工程还是后端工程,VSCode 都能提供给开发者优秀的用户体验。鉴于 VSCode 超高的流行度,我会默认…...

LearnOpenGL-高级OpenGL-6.天空盒
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject 文章目录天空盒介绍如何采样OpenGL纹理目标例子0:天空盒效果环境映射反射例子1:Cube…...

Printk打印内核日志
一、背景 Linux 内核中提供了内核日志打印的工具printk。它的使用方式C语言中的printf是类似的。接下来我们介绍一下printk的使用方式。本文以打印Binder中的日志为例,进行演示。 printk的方法声明和日志级别binder驱动中增加 打印代码android系统中查看日志信息 …...
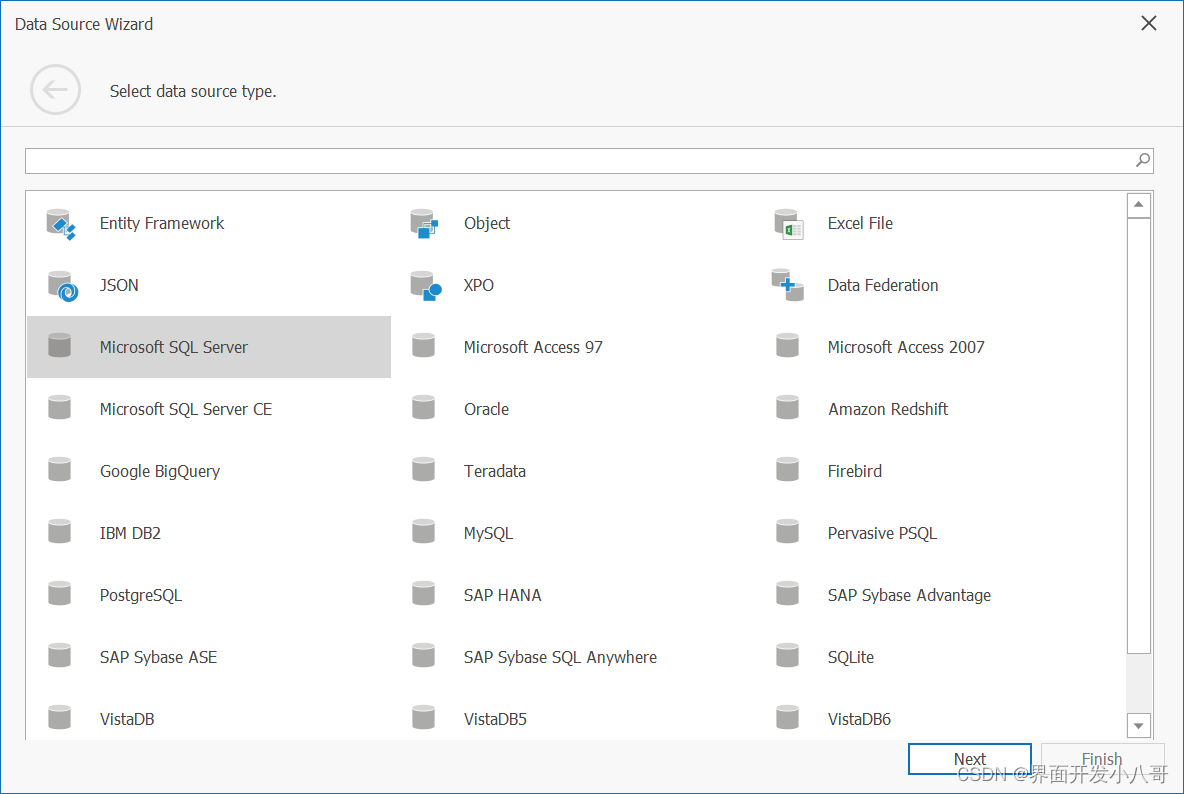
界面控件DevExpress WPF 202计划发布的新功能合集
DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至超出企业需求的高性能业务应用程序。通过DevExpress WPF能创建有着强大互动功能的XAML基础应用程序,这些应用程序专注于当代客户的需求和构建未来新一代支持触摸的解决方案。本文将介绍今年DevExpr…...

Spring Cloud Alibaba 微服务2,注册中心演变 + Nacos注册中心与配置中心
目录专栏导读一、什么是Nacos?二、注册中心演变及其设计思想1、RestTemplate调用远程服务2、通过Nginx维护服务列表(upStream)3、通过Nacos实现注册中心4、心跳版Nacos三、Nacos Discovery四、Nacos核心功能1、服务注册2、服务心跳3、服务同步…...
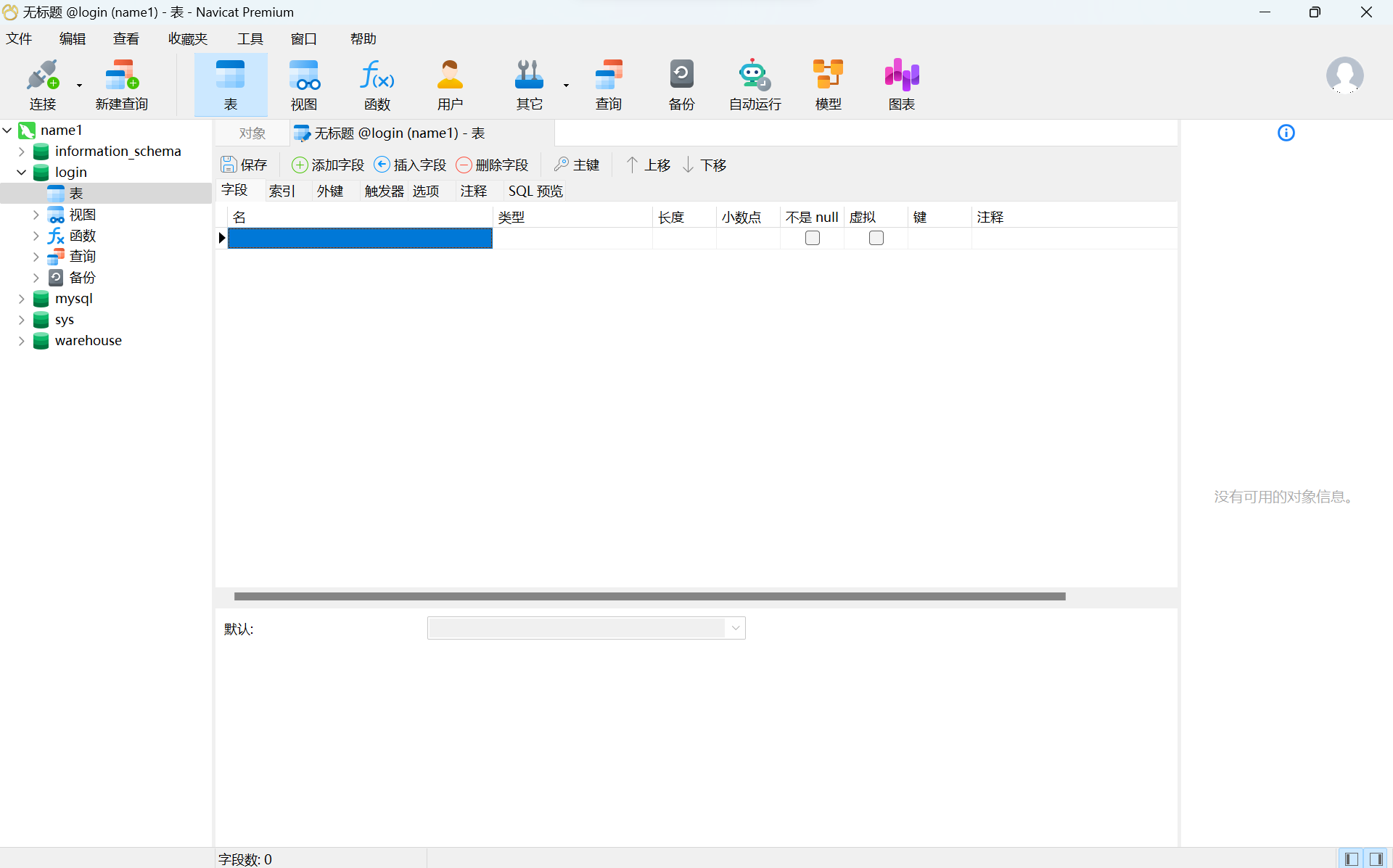
Navicat 图形化界面工具
Navicat 介绍 Navicat是一套可创建多个连接的数据库管理工具,用以方便管理 MySQL、Oracle、SQL Server等不同类型的数据库 目录 Navicat 介绍 Navicat 下载 Navicat 安装 Navicat 使用 Navicat连接MySQL数据库 Navicat创建数据库和表 Navicat 下载 1、点击这…...
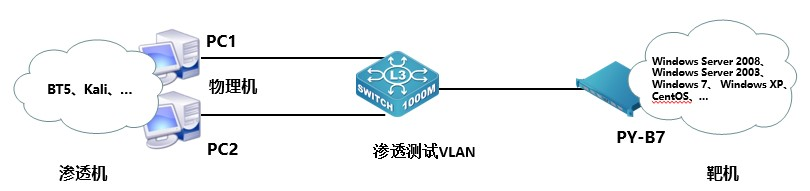
2023年网络安全比赛--attack(新)数据包分析中职组(超详细)
一、竞赛时间 180分钟 共计3小时 任务环境说明: 1 分析attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户第一次访问HTTP服务的数据包是第几号,将该号数作为Flag值提交; 2.继续查看数据包文件attack.pcapng,分析出恶意用户扫描了哪些端口,将全部的端口号…...
)
C语言之extern(七十)
extern同一个文件:修饰变量声明#include <stdio.h>int add(){extern int x,y;return x y; }int main(){printf("%d\n", add()); }int x 10; int y 20;extern文件之间:修饰函数声明<1>.add.cint sum(){extern int x ;extern in…...
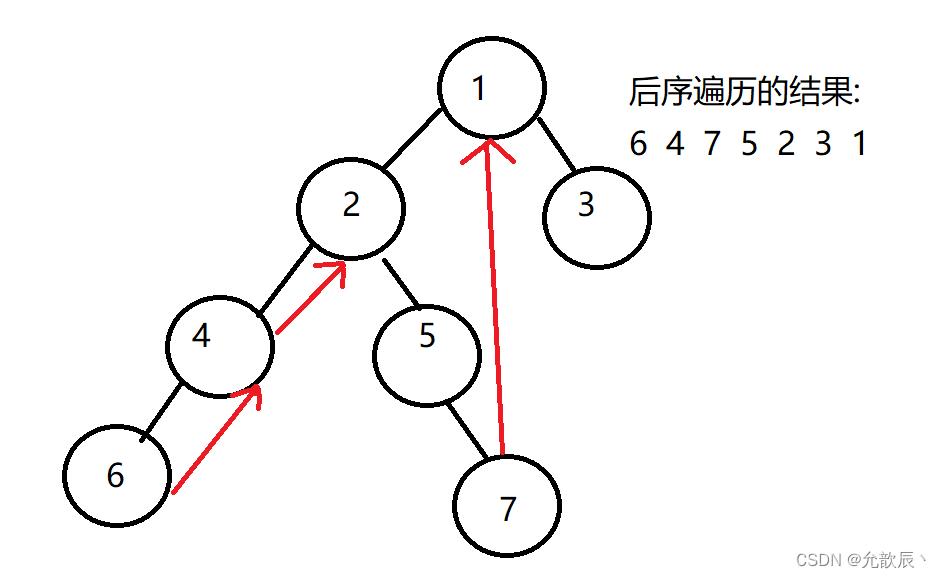
树的前中后序的Morris遍历
目录 一.Morris遍历 1.什么是Morris遍历 2.基本思想 3.Morris遍历的优点和缺点 4.知识回顾----二叉树的线索化 二.中序Morris遍历 1.中序Morris遍历的分析 2.中序Morris遍历的思路 3.具体的代码实现 三.前序Morris遍历 1.前序Morris遍历的思路 2.具体的代码实现 四…...
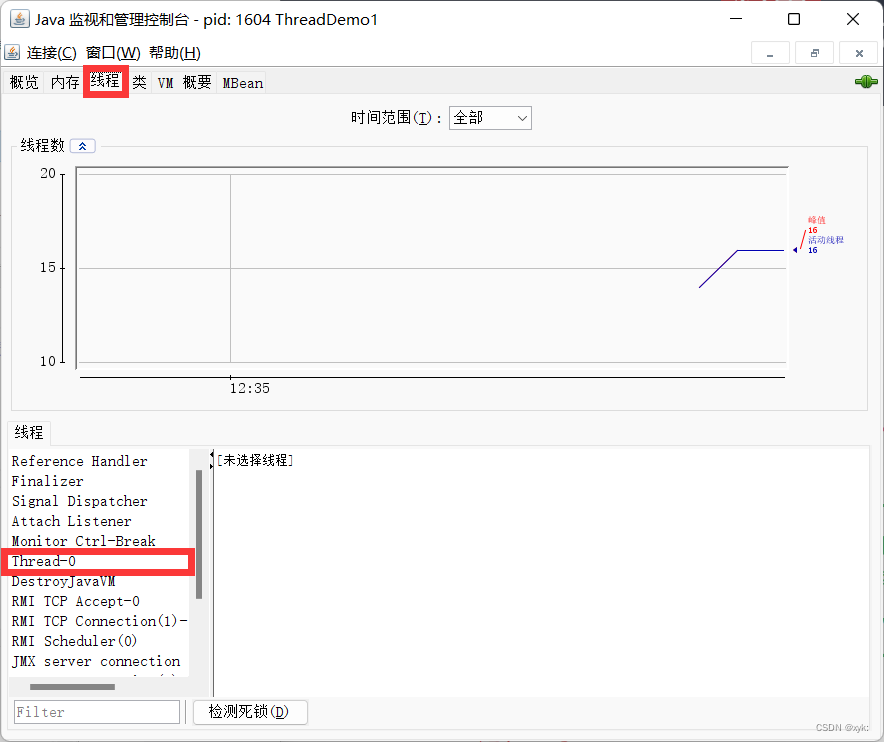
到底什么是线程?线程与进程有哪些区别?
上一篇文章我们讲述了什么是进程,进程的基本调度 http://t.csdn.cn/ybiwThttp://t.csdn.cn/ybiwT 那么本篇文章我们将了解一下什么是线程?线程与进程有哪些区别?线程应该怎么去编程? 目录 http://t.csdn.cn/ybiwThttp://t.csdn…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
