OPPO 2024届校招正式批笔试题-后端(C卷)
小欧的括号嵌套
题目描述
小欧想要构造一个合法的括号序列满足以下条件:
- 括号序列长度恰好为 2 × n 2×n 2×n。
- 括号序列的嵌套层数最大值为 r r r。
括号嵌套层数是指在一个字符串中,以左括号 “(” 和右括号 “)” 形成的括号对的最大嵌套深度。
输入描述
一行两个整数 n , r ( 1 ≤ r ≤ n ≤ 1 0 5 ) n, r(1 ≤ r ≤ n ≤ 10^5) n,r(1≤r≤n≤105)。
输出描述
一行一个字符串表示括号序列。若有多种构造方案,输出任意一个即可。
解题思路
构造一种特殊的满足条件的括号序列即可。
代码实现
int main() {int n, r;scanf("%d%d", &n, &r);string s = string(r, '(') + string(r, ')');for (int k = n / r; k-- > 0; cout << s);cout << string(n % r, '(') + string(n % r, ')');return 0;
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
小欧的等差数列
题目描述
小欧有一个长度为 n n n,首项为 a a a,公差为 d d d 的等差数列。现在,小欧把这 n n n 个数看作一个集合,每次操作可以从集合中任意选两个数 a i , a j a_i,a_j ai,aj,如果 a i + a j a_i+a_j ai+aj 是偶数,那么可以将 ( a i + a j ) / 2 (a_i+a_j)/2 (ai+aj)/2 加入到集合中。小欧想知道,经过若干次操作后,集合中最多能有多少个数。
输入描述
一行三个整数 n , a , d n, a, d n,a,d,表示等差数列的长度,首项和公差。
- 1 ≤ n ≤ 1 0 5 1 ≤ n ≤ 10^5 1≤n≤105
- 1 ≤ a , d ≤ 1 0 9 1 ≤ a, d ≤ 10^9 1≤a,d≤109
输出描述
输出一个整数,表示集合中最多能有多少个数。
解题思路
- a i + a j a_i + a_j ai+aj = a + i × d + a + j × d a+i×d+a+j×d a+i×d+a+j×d
- 若 i + j i+j i+j 为偶数,则 ( a i + a j ) (a_i+a_j) (ai+aj) 为偶数,但 ( a i + a j ) / 2 (a_i+a_j)/2 (ai+aj)/2 已存在于集合中。
- 若 d d d 为偶数,则 ( a i + a j ) (a_i+a_j) (ai+aj) 为偶数,此时 ( a i + a j ) / 2 (a_i+a_j)/2 (ai+aj)/2 不一定在集合中。
- 若由集合衍生的数 x x x 在 a , a + d a,a+d a,a+d 之间,那么 x x x 必然可以由 a , a + d a,a+d a,a+d 衍生得到, a + k × d , a + ( k + 1 ) × d a+k×d,a+(k+1)×d a+k×d,a+(k+1)×d 同理。
- 所以,仅需考虑由 a , a + d a,a+d a,a+d 可以衍生得到多少数即可。
- 若 d d d 的因数包含 2 k 2^k 2k,那么,由 a , a + d a,a+d a,a+d 可以衍生得到 2 k − 1 2^k-1 2k−1 个数,由集合可衍生得到的数的个数为 ( 2 k − 1 ) × ( n − 1 ) (2^k-1) × (n-1) (2k−1)×(n−1)。
代码实现
int main() {long long n, a, d, k = 0;cin >> n >> a >> d;while (!(d & 1))k++, d >>= 1;cout << n + ((1 << k) - 1) * (n - 1);return 0;
}
时间复杂度: O ( 1 ) O(1) O(1)。
空间复杂度: O ( 1 ) O(1) O(1)。
小欧喝水
小欧拿了 n n n 个杯子排成了一排,其中有 k k k 个杯子装满了水,剩余的 n − k n-k n−k 个杯子为空的。小欧每回合的操作如下:
- 随机选择一个杯子。
- 杯子是空的。回合直接结束。
- 杯子是满的。如果小欧上一回合喝过了水,则回合结束;否则将喝完这杯水,回合结束。
小欧想知道,她喝完所有水的回合数期望是多少?
输入描述
两个正整数 n , k n,k n,k,用空格隔开。
- 1 ≤ k ≤ n ≤ 1 0 6 1≤ k ≤ n ≤ 10^6 1≤k≤n≤106
输出描述
一个浮点数,代表期望的回合数。如果你的答案和正确答案的误差不超过 1 0 − 6 10^{-6} 10−6,则认为答案正确。
解题思路
本题留给读者小试牛刀。
END
题目来源:OPPO 2024届校招正式批笔试题-后端(C卷)
文章声明:题目来源 牛客 平台,如有侵权,请联系删除!
相关文章:
)
OPPO 2024届校招正式批笔试题-后端(C卷)
小欧的括号嵌套 题目描述 小欧想要构造一个合法的括号序列满足以下条件: 括号序列长度恰好为 2 n 2n 2n。括号序列的嵌套层数最大值为 r r r。 括号嵌套层数是指在一个字符串中,以左括号 “(” 和右括号 “)” 形成的括号对的最大嵌套深度。 输入…...

HTTP请求五类状态码详细介绍,以及部分处理思路
HTTP请求状态码分为五类: 一. 消息系列 二 成功系列 三. 重定向系列 四. 请求错误系列 五. 服务器端错误系列 302:临时转移成功,请求的内容已转移到新位置 403:禁止访问 500:服务器内部错误 401代表未授权。 以下是常见的一些状态码: 1xx&…...
)
Log4j的原理及应用详解(三)
本系列文章简介: 在软件开发的广阔领域中,日志记录是一项至关重要的活动。它不仅帮助开发者追踪程序的执行流程,还在问题排查、性能监控以及用户行为分析等方面发挥着不可替代的作用。随着软件系统的日益复杂,对日志管理的需求也日益增长,因此,一个高效、灵活且易于使用的…...

【深度学习】PyTorch框架(4):初始网络、残差网络 和密集连接网络
1、引言 在本篇文章中,我们将深入探讨并实现一些现代卷积神经网络(CNN)架构的变体。近年来,学界提出了众多新颖的网络架构。其中一些最具影响力,并且至今仍然具有重要地位的架构包括:GoogleNet/Inception架…...

【关于PHP性能优化,内存优化,日志工具等问题处理】
目录 PHP 性能优化: 如何优化 PHP 代码以提高性能? 通用优化策略: 框架特定优化: 性能优化最佳实践: 描述一下你使用过的 PHP 性能分析工具。 检测内存泄漏的方法 使用工具检测内存泄漏 常见内存泄漏场景及解决…...

R-CNN、Fast R-CNN和Faster R-CNN:目标检测的进化之路
在计算机视觉的世界里,目标检测是一个重要的任务,它的目标是找到图像中的特定物体,并标注出它们的位置。这项技术广泛应用于自动驾驶、安防监控等领域。为了让计算机能够准确高效地完成这一任务,科学家们提出了许多优秀的算法,其中最具代表性的就是R-CNN、Fast R-CNN和Fas…...

Yolov8网络结构学习
详解YOLOv8网络结构/环境搭建/数据集获取/训练/推理/验证/导出/部署 深入解析YOLOv8:网络结构与推理过程 YOLO? You Know! --YOLOV8详解 一:yolov8总体结构 1.Backbone:它采用了一系列卷积和 反卷积层只来提取特征,同时也使用了残差连接和…...

5.5 软件工程-系统测试
系统测试 - 意义和目的 系统测试 - 原则 系统测试 - 测试过程 系统测试 - 测试策略 系统测试 - 测试方法 真题 系统测试 - 测试用例设计 黑盒测试 白盒测试 真题 系统测试 - 调试 系统测试 - 软件度量 真题...

网络故障处理及分析工具:Wireshark和Tcpdump集成
Wireshark 是一款免费的开源数据包嗅探器和网络协议分析器,已成为网络故障排除、分析和安全(双向)中不可或缺的工具。 本文深入探讨了充分利用 Wireshark 的功能、用途和实用技巧。 无论您是开发人员、安全专家,还是只是对网络操…...

UDP客户端、服务端及简易聊天室实现 —— Java
UDP 协议(用户数据包协议) UDP 是无连接通信协议,即在数据传输时,数据的发送端和接收端不建立逻辑连接,简单来说,当客户端向接收端发送数据时,客户端不会确认接收端是否存在,就会发出…...

下载安装nodejs npm jarn笔记
下载安装nodejs npm jarn笔记 下载 Node.js安装Node.js修改node全局路径安装yarn 下载 Node.js 下载Node.js 安装Node.js 双击下载的下来的.msi文件运行并安装一直点next。安装路径可以是默认也可自定义。安装完成后Node.js和npm就安装完成了 命令行输入: nod…...
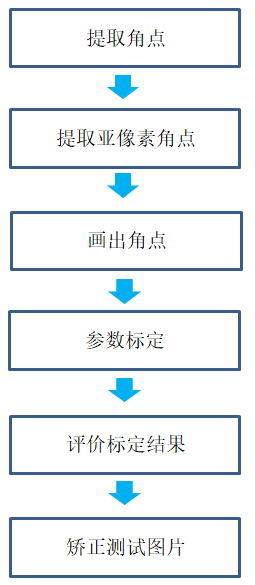
Calibration相机内参数标定
1.环境依赖 本算法采用张正友相机标定法进行实现,内部对其进行了封装。 环境依赖为 ubuntu20.04 opencv4.2.0 yaml-cpp yaml-cpp安装方式: (1)git clone https://github.com/jbeder/yaml-cpp.git #将yaml-cpp下载至本地 &a…...

MySQL源码安装
安装MySQL 本次安装使用的是绿色硬盘版本,无需额外安装依赖环境,比较简单 cd /opt tar -xf mysql安装包 mv 解压出的目录 /usr/local/mysql #创建程序用户 useradd -M -s /sbin/nologin mysql #mysql的主配置文件设定所属用户和组 chown -R mysql.m…...

gtest单元测试:进程冻结与恢复管理模块的单元测试实现
文章目录 1. 概要2. 进程管理接口详解2.1 进程冻结与恢复的基本概念2.2 进程查找与PID获取2.3 进程冻结与恢复的实现2.3.1 进程冻结2.3.2 进程恢复 2.4 进程终止2.5 进程状态监控与控制 3. dummy_process的设计与实现3.1 创建dummy_process脚本3.2 启动dummy_process3.3 终止du…...

Flutter动画详解第二篇之显式动画(Explicit Animations)
目录 前言 一、定义 1.AnimationController 1.常用属性 1. value 2. status 3. duration 2.常用方法 1.forward 2.reverse 3.repeat 4.stop 5. reset 6. animateTo(double target, {Duration? duration, Curve curve Curves.linear}) 7.animateBack(double ta…...
)
python常用模块(JSON与pickle、Os模块)
一、Open函数使用 在python中,open() 函数用于打开文件,并返回一个文件对象,同时支持读取和写入文件。 基本用法: file open(file_path, moder, encodingNone, newlineNone) 其中file_path表示的是文件的路径,可以…...

MMLab-dataset_analysis
数据分析工具 这里写目录标题 数据分析工具dataset_analysis.py数据可视化分析 benchmark.pybrowse_coco_json.pybrowse_dataset.pyOptimize_anchors mmyolo、mmsegmentation等提供了数据集分析工具 dataset_analysis.py 数据采用coco格式数据 根据配置文件分析全部数据类型或…...

艺术与技术的交响曲:CSS绘图的艺术与实践
在前端开发的世界里,CSS(层叠样式表)作为网页布局和样式的基石,其功能早已超越了简单的颜色和间距设置。近年来,随着CSS3的普及,开发者们开始探索CSS在图形绘制方面的潜力,用纯粹的代码创造出令…...

基于 JAVA 的旅游网站设计与实现
点击下载源码 塞北村镇旅游网站设计 摘要 城市旅游产业的日新月异影响着村镇旅游产业的发展变化。网络、电子科技的迅猛前进同样牵动着旅游产业的快速成长。随着人们消费理念的不断发展变化,越来越多的人开始注意精神文明的追求,而不仅仅只是在意物质消…...

【C++深度探索】二叉搜索树的全面解析与高效实现
🔥 个人主页:大耳朵土土垚 🔥 所属专栏:C从入门至进阶 这里将会不定期更新有关C/C的内容,欢迎大家点赞,收藏,评论🥳🥳🎉🎉🎉 文章目录…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
