智能优化算法之灰狼优化算法(GWO)的实现(Python附源码)
文章目录
- 一、灰狼优化算法的实现思路
- 1、社会等级结构分级
- 2、包围猎物
- 3、攻击猎物
- 4、搜索猎物
- 二、算法步骤
- 三、实例
一、灰狼优化算法的实现思路
灰狼优化算法(Grey Wolf Optimizer,简称GWO)是由Seyedali Mirjalili等人于2014年提出的一种群智能优化算法,这一算法主要由自然界中的灰狼群体的捕食行为启发而来,灰狼是一种群居动物,一般群体中由5到12个个体构成,与一般动物群体不同的是,这一群体中存在十分严格的社会主导阶层,且与金字塔结构十分相似,主要由四个层级构成。
首先最高的层级可以被称为α,它们主要对种群中的各种规则进行制定,如狩猎地点、休息地点等,整个种群都会听从它们的决定。然后第二个层级被称为β,这一层级的灰狼个体主要帮助α制定相关决策,同时将各种决策上出现的问题反馈给α狼,它在整个种群中的地位仅次于α狼,因此低等级的灰狼个体也必须听命于β狼。紧接着的一个阶级为δ,这一个层级扮演着执行者的角色并将α狼与β狼制定的规则与命令付诸行动,它们可以是哨兵、侦查者、猎人,甚至是种群中受伤狼群的看护者。最后一个层级为ω,这个层级的灰狼个体为最弱势的个体,它们一般为种群中年迈或残疾的个体,因此它们只能去服从前面每个层级的灰狼个体。
结合上述思想,可以将灰狼优化算法的原理归为四个基本行为,它们分别为社会等级结构分级、搜索猎物、包围猎物以及攻击猎物,下面将分别从这四个基本行为进行介绍。
1、社会等级结构分级
该算法为了符合灰狼群体的社会等级结构,将候选解决方案的优劣性作为评判的标准,另外由于解决方案的独特性,因此将前三个等级α、β以及δ的数量设定为一个,即将候选解决方案中表现最优的方案设为α,第二个与第三个最优解决方案分别设定为β与δ,其余的解决方案则均为ω。按照等级较低的灰狼个体跟随等级较高的灰狼个体规则,ω解决方案将不断学习α、β以及δ解决方案以获得更好的表现。
2、包围猎物
针对灰狼群体包围猎物的特性,使用下列公式对其行为进行描述:


其中t为当前迭代次数,A ⃗和C ⃗为系数向量,(X_p ) ⃗为灰狼个体的位置向量,X ⃗为灰狼个体的位置信息。
A ⃗和C ⃗将分别通过下面两个公式计算得出:


其中a ⃗将随着迭代的次数由2到0线性递减,r1与r2均为0到1之间的随机向量。
3、攻击猎物
通过包围行为,所有灰狼个体将猎物控制在一个包围圈内,之后ω狼将在α、β以及δ狼的引导下进行捕猎,由于目前猎物的位置是未知的,而代表最优解决方案的灰狼α、β以及δ的位置信息是已知的,因此ω狼将通过学习灰狼α、β以及δ的位置信息来进行移动以完成对猎物的捕食。下面几个公式代表了灰狼个体的捕食行为:



由上述公式可以了解到,猎物的位置是随机的,灰狼个体将通过学习灰狼α、β以及δ的位置信息在猎物附近进行随机移动,以此来估计猎物的具体位置。
4、搜索猎物
在灰狼种群开始了对猎物的随机包围时,对猎物的搜索过程也在随之展开,由攻击猎物的原理过程可以了解到,A ⃗这一系数向量的大小将会直接影响到灰狼个体位置的移动,在整个迭代过程中,除了A ⃗的绝对值小于1外,还存在A ⃗的绝对值大于1的情况,在这种条件下,灰狼个体将向包围圈周围扩张,以此发现更多猎物可能存在的位置。即当|A|≥1时,候选解决方案倾向于偏离当前猎物,当|A|<1时,候选解决方案逐渐收敛于猎物的位置。
除系数向量A ⃗之外,还存在一个系数向量C ⃗,C ⃗通常是0到2之间的一个随机值,这一向量的角色类似于为猎物位置信息新添一个随机权重,在自然界中,灰狼种群对猎物的捕食通常不会是顺利的,有时会出现一定的障碍对整个搜索行为进行影响,使得灰狼种群无法直接快速得接近猎物,系数向量C ⃗则可以在为整个搜索过程增加一个随机性的同时使整个灰狼种群在优化过程中表现出更随机的行为,以此来探索更多区域并避免陷入局部最优。
二、算法步骤
使用灰狼优化算法对优化问题进行求解时的具体步骤可以归纳如下:
- 以种群个体的位置信息作为待优化问题的解,根据待优化问题的解的范围,随机初始化种群所有个体的位置信息;
- 初始化参数a ⃗,A ⃗和C ⃗;
- 根据待优化问题,计算每个种群个体的适应度值,并对其进行排序,适应度值越高,则个体的位置信息越接近最优解,将适应度值排在前三个个体分别设定为灰狼α、β以及δ,并保存当前最优的位置信息;
- 依次对种群中每个个体的位置信息进行更新;
- 针对每个个体更新后的位置信息,重新进行适应度值的计算,根据新的适应度值的大小更新灰狼α、β与δ的位置信息以及历史最优的位置信息,更新参数a ⃗,A ⃗和C ⃗;
- 根据迭代的次数重复步骤3到步骤5,当达到最大迭代次数时停止迭代过程,输出历史最优的位置信息,该位置信息即为算法优化后获得的最优解。
三、实例
待求解问题:
Rosenbrock’s,取值范围为[-10,10],取值范围内的理想最优解为0,将其搜索的空间维度设为20。

实现源码:
#库的导入
import numpy as np
import matplotlib.pyplot as plt
import heapq#待求解问题,求解问题为求最小值
def function(x):y1 = 0for i in range(len(x)-1):y2 = 100*((x[i+1] - x[i]**2)**2)+(x[i]-1)**2y1 = y1 + y2y = abs(0 - y1)return ym = 30 #种群数量
imax = 100 #迭代次数
dimen = 20 #解的搜索维度
rangelow = -10 #解的最小取值
rangehigh = 10 #解的最大取值
amax = 2 #系数向量初始值#pop用于存储种群个体的位置信息,pop_fitness用于存储个体对应的适应度值
pop = np.zeros((m,dimen))
pop_fitness = np.zeros(m)
#对种群个体进行初始化并计算对应适应度值
for j in range(m):pop[j] = np.random.uniform(low=rangelow, high=rangehigh,size=(1, dimen))pop_fitness[j] = function(pop[j])#allbestpop,allbestfit分别存储种群在历史迭代过程中最优个体解及对应适应度
allbestpop,allbestfit = pop[pop_fitness.argmin()].copy(),pop_fitness.min()#通过排序找出种群中适应度值最优的前三个个体,并获得它们的位置信息
pop_fitness1 = pop_fitness.flatten()
pop_fitness1 = pop_fitness1.tolist()
three = list(map(pop_fitness1.index, heapq.nsmallest(3, pop_fitness1)))
Xalpha = pop[three[0]]
Xbeta = pop[three[1]]
Xdelta = pop[three[2]]#his_bestfit存储每次迭代时种群历史适应度值最优的个体适应度
his_bestfit=np.zeros(imax)#开始训练
for i in range(imax):print("The iteration is:", i + 1)#对系数向量的计算参数a进行计算iratio = i / imaxa = amax * (1 - iratio)#对每个个体进行位置更新for j in range(m):#分别计算在适应度值最优的前三个个体的影响下,个体的位置移动量X1、X2、X3C1 = 2 * np.random.rand()Dalpha = np.abs(C1 * Xalpha - pop[j])A1 = 2 * a * np.random.rand() - aX1 = Xalpha - A1 * DalphaC2 = 2 * np.random.rand()Dbeta = np.abs(C2 * Xbeta - pop[j])A2 = 2 * a * np.random.rand() - aX2 = Xbeta - A2 * DbetaC3 = 2 * np.random.rand()Ddelta = np.abs(C3 * Xdelta - pop[j])A3 = 2 * a * np.random.rand() - aX3 = Xdelta - A3 * Ddelta#计算个体移动后的位置及适应度值pop[j] = (X1 + X2 + X3) / 3pop_fitness[j] = function(pop[j])#对种群历史最优位置信息与适应度值进行更新if pop_fitness.min() < allbestfit:allbestfit = pop_fitness.min()allbestpop = pop[pop_fitness.argmin()].copy()#通过排序找出种群中适应度值最优的前三个个体,并获得它们的位置信息pop_fitness1 = pop_fitness.flatten()pop_fitness1 = pop_fitness1.tolist()three = list(map(pop_fitness1.index, heapq.nsmallest(3, pop_fitness1)))Xalpha = pop[three[0]]Xbeta = pop[three[1]]Xdelta = pop[three[2]]#存储当前迭代下的种群历史最优适应度值并输出his_bestfit[i] = allbestfitprint("The best fitness is:", allbestfit)
print("After iteration, the best pop is:",allbestpop)
print("After iteration, the best fitness is:","%e"%allbestfit)#输出训练后种群个体适应度值的均值与标准差
mean = np.sum(pop_fitness)/m
std = np.std(pop_fitness)
print("After iteration, the mean fitness of the swarm is:","%e"%mean)
print("After iteration, the std fitness of the swarm is:","%e"%std)
#将结果进行绘图
fig=plt.figure(figsize=(12, 10), dpi=300)
plt.title('The change of best fitness',fontdict={'weight':'normal','size': 30})
x=range(1,101,1)
plt.plot(x,his_bestfit,color="red",label="GWO",linewidth=3.0, linestyle="-")
plt.tick_params(labelsize=25)
plt.xlim(0,101)
plt.yscale("log")
plt.xlabel("Epoch",fontdict={'weight':'normal','size': 30})
plt.ylabel("Fitness value",fontdict={'weight':'normal','size': 30})
plt.xticks(range(0,101,10))
plt.legend(loc="upper right",prop={'size':20})
plt.savefig("GWO.png")
plt.show()
图中横轴为迭代次数,纵轴为最优适应度值。

参考源码
相关文章:

智能优化算法之灰狼优化算法(GWO)的实现(Python附源码)
文章目录一、灰狼优化算法的实现思路1、社会等级结构分级2、包围猎物3、攻击猎物4、搜索猎物二、算法步骤三、实例一、灰狼优化算法的实现思路 灰狼优化算法(Grey Wolf Optimizer,简称GWO)是由Seyedali Mirjalili等人于2014年提出的一种群智…...

leetCode热题10-15 解题代码,思路
前言 计划做一系列算法题的文章,因为自己这块确实比较薄弱,但又很重要!写这篇文章前,我已经刷了一本剑指offer,leetcode top150道,牛客某题库106道 这个样子吧,感觉题量算是入门了吧࿱…...

同步辐射GISAXS和GIWAXS的原理及应用领域
同步辐射GISAXS和GIWAXS是两种常用的同步辐射X射线衍射技术,它们在材料科学、化学、生物学、物理学等领域中广泛应用。本文将从原理、实验方法和应用三个方面,对同步辐射GISAXS和GIWAXS进行描述和比较。 一、原理 GISAXS和GIWAXS都是利用X射线与样品相互…...

OpManager 进行网络性能管理
计算机网络构成了任何组织的 IT 基础架构的支柱。由于企业严重依赖基于互联网的应用程序,由于网络相关问题,最终用户不受影响非常重要。因此,借助网络管理解决方案监控和提高网络性能对于保持企业始终正常运行至关重要。这将确保维护服务级别…...

面试被问到向上转型和向下转型时,怎么回答?
目录 前置小知识 1、向上转型 补充:向上转型的三种情况 2、向下转型 使用关键字:instanceof 3、转型带来了什么好处 前置小知识 java中的继承,我们简单回顾一下 通过java中的继承机制,可以实现一个类继承另一个类ÿ…...

加密月解密:概述,基础篇
加密月解密:概述,基础篇 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle&…...
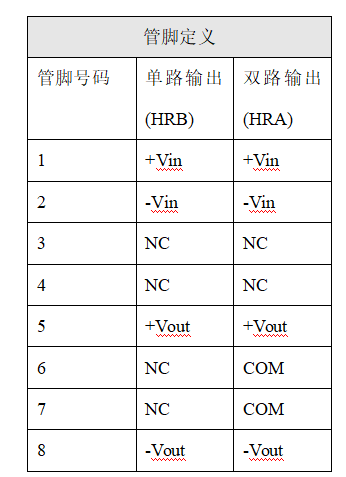
DC-DC升压模块隔离高压稳压电源直流变换器12v24v48v转600V1000V1100V1500V2000V3000V
特点● 效率高达 80%● 2*2英寸标准封装● 单双电压输出● 价格低● 大于600V高压,稳压输出● 工作温度: -40℃~85℃● 阻燃封装,满足UL94-V0 要求● 温度特性好● 可直接焊在PCB 上应用HRB W1~25W 系列模块电源是一种DC-DC升压变换器。该模块电源的输入电压分为&am…...
pandas数据分析(三)
书接pandas数据分析(二) 文章目录DataFrame数据处理与分析处理超市交易数据中的异常值处理超市交易数据中的缺失值处理超市交易数据中的重复值使用数据差分查看员工业绩波动情况使用透视表与交叉表查看业绩汇总数据使用重采样技术按时间段查看员工业绩Da…...

cpu performance profiling
精彩文章分享1. android performanceAndroid 性能分析工具介绍 (qq.com)手机Android存储性能优化架构分析 (qq.com)抖音 Android 性能优化系列:启动优化之理论和工具篇 (qq.com)那些年,我们一起经历过的 Android 系统性能优化 (qq.com)Android卡顿&#…...

vue2启动项目npm run dev报错 Error: Cannot find module ‘babel-preset-es2015‘ 修改以及问题原因
报错内容如下图: 说找不到模块 babel-preset-es2015。 在报错之前,我正在修改代码,使用 ElementUI 的按需引入方式,修改了 babel.config.js 。 注意:vue/cli 脚手架4版本已经使用了 babel7 ,所以项目中…...
*9 set up 注意点
1、set up 执行的时机:beforeCreate 之前执行一次,this 是 undefined 2、set up 的参数: props:值为对象,组件外传递属性,内部声明并且接收属性 context:上下文对象,其内部包含三个…...
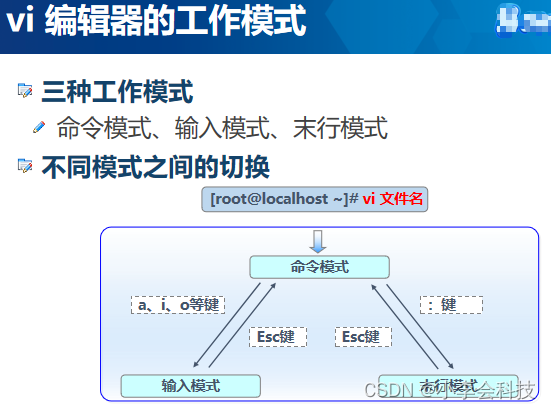
linux目录——文件管理
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。座右铭:海不辞水,故能成其大;山不辞石,故能成其高。个人主页:小李会科技的…...
使用new bing简易教程
申请new bing 首先先申请new bing然后等待通过,如下图 申请完,用edge浏览器,若有科学方法,就能在右上角的聊天进行向AI提问 使用插件来进行直接访问New Bing 在edge浏览器中安装一个插件,地址为:Mod…...

idea插件分享 显著提高开发效率
idea插件 Prettier 作用:支持代码格式化(java、js等) 另外支持js内方法跳转和js中ajax请求跳转到java代码里面 下载:Prettier SQL Params Setter 作用:将日志中mapper输出preparing和paramters处理成完整可直接执行…...

文心一言发布我怎么看?
文心一言发布会 有想看发布会视频的朋友,关注爱书不爱输的程序猿,私信找我拿 我只简短的回答两个问题: 1.文心一言能否为百度止颓? 首先,百度的颓势是由于多种因素导致的,包括市场竞争压力、业务发展战略的失误、管理体制的问题等。要想止颓,…...

100. 增减序列
给定一个长度为 n 的数列 a1,a2,…,an,每次可以选择一个区间 [l,r],使下标在这个区间内的数都加一或者都减一。 求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。 输入…...
操作系统之进程的初步认识(1)
进程1. 进程的相关概念1.1 进程的定义1.2 进程的概念(1)1.3 进程的概念(2)2. 进程和程序的区别3. 进程管理:3.1 进程的结构体有哪些属性(1) Pid(操作系统里指进程识别号)(2) 内存指针(3) 文件描述符表4. 进程调度:(1) 并行(2) 并发5. 进程调度需要的属性(1) 进程状态(2) 进程优…...

【Java】你真的懂封装吗?一文读懂封装-----建议收藏
博主简介:努力学习的预备程序媛一枚~博主主页: 是瑶瑶子啦所属专栏: Java岛冒险记【从小白到大佬之路】 前言 write in the front: 如何理解封装? 试想:我们使用微波炉的时候,只用设置好时间,按下“开始”…...

使用MobaXterm ssh远程登录Ubuntu 20.04
使用MobaXterm 远程登录Ubuntu 20.04 首先需要到官网下载一个MobaXterm 准备一台Ubuntu20.04的虚拟机。使用ifconfig查看IP 我这里的虚拟机是新安装的,所以会提示命令不存在,只要按照提示输入: sudo apt install net-tools接着等待安装完成…...
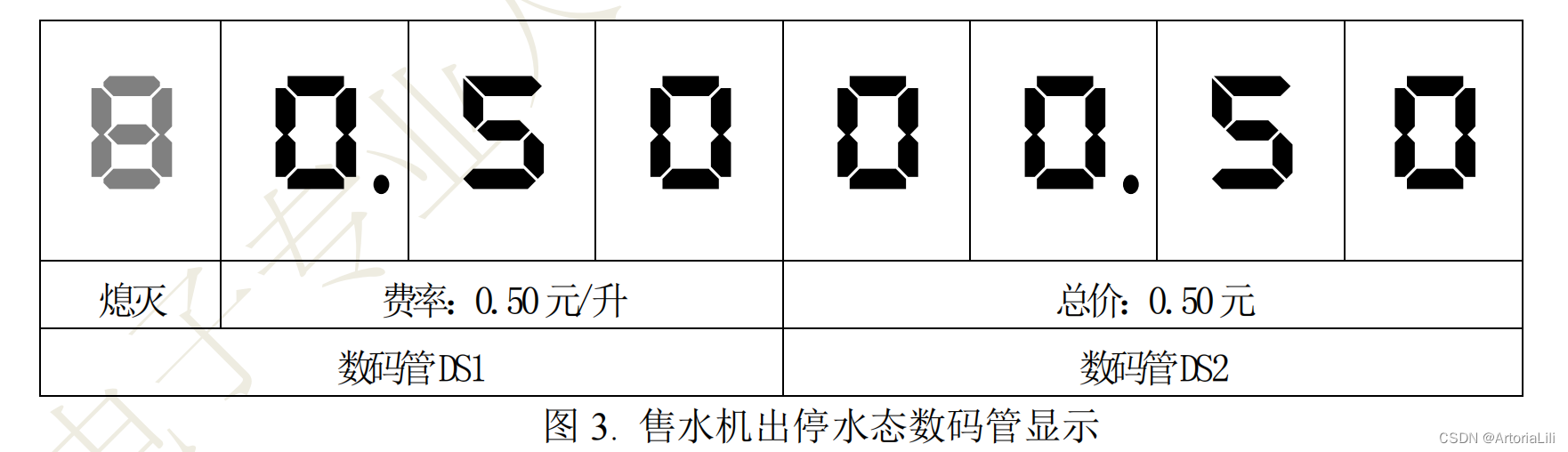
蓝桥杯历年真题训练
2012年第四届全国电子专业人才设计与技能大赛“自动售水机”设计任务书1. 系统框图接下来我们将任务分块: 1. 按键控制单元 设定按键 S7 为出水控制按键,当 S7 按下后,售水机持续出水(继电器接通,指示 灯 L10 点亮&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
