HDU1005——Number Sequence,HDU1006——Tick and Tick,HDU1007——Quoit Design
目录
HDU1005——Number Sequence
题目描述
超时代码
代码思路
正确代码
代码思路
HDU1006——Tick and Tick
题目描述
运行代码
代码思路
HDU1007——Quoit Design
题目描述
运行代码
代码思路
HDU1005——Number Sequence
题目描述
Problem - 1005

超时代码
#include <iostream>
using namespace std;
int f(int A, int B, int n) {int f1 = 1, f2 = 1, fn;if (n == 1 || n == 2) {return 1;}for (int i = 3; i <= n; i++) {fn = (A * f1 + B * f2) % 7;f2 = f1;f1 = fn;}return fn;
}
int main() {int A, B, n;while (true) {cin >> A >> B >> n;if (A == 0 && B == 0 && n == 0) {break;}cout << f(A, B, n) << endl;}return 0;
}代码思路
-
函数
f:- 定义了三个变量
f1,f2, 和fn分别代表序列中的前两个值和当前计算的值。 - 如果
n是1或者2,函数直接返回1,这可以看作是序列的初始条件。 - 当
n大于2时,进入一个循环,从3到n:- 每次迭代计算
fn为A乘以f1加上B乘以f2的结果,并对7取模。 - 然后更新
f1和f2的值以便下一次迭代。
- 每次迭代计算
- 循环结束后,返回
fn。
- 定义了三个变量
-
主函数
main:- 无限循环读取用户输入的
A,B, 和n值,直到遇到所有为0的终止条件。 - 调用
f函数并打印结果。 - 当输入
A,B, 和n全部为0时,循环结束,程序退出。
- 无限循环读取用户输入的
![]()
这个结果最后是超时运算
正确代码
#include <iostream>
#include <vector>
#include <cmath>
#include <string>
#include <algorithm>
using namespace std;
int f[100];
int length, st; // 循环节长度和循环开始的标记bool finda(int n) {int a = f[n - 1], b = f[n];// 使用更高效的搜索算法,如二分查找int left = 1, right = n - 2;while (left <= right) {int mid = left + (right - left) / 2;if (f[mid] == a && f[mid + 1] == b) {st = mid;length = n - 1 - mid;return true;}else if (f[mid] < a || (f[mid] == a && f[mid + 1] < b)) {left = mid + 1;}else {right = mid - 1;}}return false;
}int main() {int a, b, n;while (true) {cin >> a >> b >> n;if (a == 0)break;f[1] = 1; f[2] = 1;for (int i = 3; i < 100; i++) {// 预先计算乘法结果,避免重复计算int prev1Mult = a * f[i - 1];int prev2Mult = b * f[i - 2];f[i] = (prev1Mult + prev2Mult) % 7;if (finda(i))break;}if (n < st)cout << f[n] << endl;elsecout << f[(n - st) % length + st] << endl;}
}代码思路
-
初始化序列:数组
f[]用来存储序列的值。length和st变量分别用于记录循环节的长度和循环节开始的位置。 -
计算序列:
- 使用循环从第三项开始计算序列的值,直到检测到循环节或者达到预设的上限(这里是100项)。
- 每一项计算使用了预先计算的乘法结果(
prev1Mult和prev2Mult),这有助于减少重复计算,提高效率。
-
检测循环节:函数
finda()通过二分查找算法检测序列中的循环节。一旦找到重复的模式(即连续两项相同),它会记录循环节的开始位置(st)和长度(length)。 -
输出结果:
- 根据用户输入的nn,如果nn小于循环节开始的位置,直接输出
f[n]。 - 如果nn大于等于循环节开始的位置,则输出循环节中对应位置的值,即
f[(n - st) % length + st]。
- 根据用户输入的nn,如果nn小于循环节开始的位置,直接输出
这种算法特别适用于计算周期性出现的序列,通过检测循环节可以极大地优化计算过程,尤其是在需要频繁查询大索引位置的场景下。
HDU1006——Tick and Tick
题目描述
Problem - 1006

运行代码
#include <iostream>
#include <stdio.h>
#include <algorithm>const double sm = 59.0 / 10, sh = 719.0 / 120, mh = 11.0 / 120;
const double t_sm = 360 * 10.0 / 59, t_sh = 360 * 120.0 / 719, t_mh = 360 * 120.0 / 11;using namespace std;// 定义最大值最小值函数
double Min(double a, double b, double c) {return min(c, min(a, b));
}double Max(double a, double b, double c) {return max(c, max(a, b));
}int main()
{double D;while (cin >> D && D != -1) {double b_sm, b_sh, b_mh, e_sm, e_sh, e_mh, start, finish, sum = 0;if (D == 0) {sum = 100;printf("%.3lf\n", 100.0);continue;}// 第一次满足条件的时间b_sm = D / sm;b_sh = D / sh;b_mh = D / mh;// 第一次不满足条件的时间e_sm = (360 - D) / sm;e_sh = (360 - D) / sh;e_mh = (360 - D) / mh;// 使用简洁的循环条件double b1 = b_sm, e1 = e_sm;while (e1 <= 12 * 60 * 60) {double b2 = b_sh, e2 = e_sh;while (e2 <= 12 * 60 * 60) {if (e2 < b1) {b2 += t_sh;e2 += t_sh;continue;}if (b2 > e1) {break;}double b3 = b_mh, e3 = e_mh;while (e3 <= 12 * 60 * 60) {if (e3 < b2 || e3 < b1) {b3 += t_mh;e3 += t_mh;continue;}if (b3 > e1 || b3 > e2) {break;}start = Max(b1, b2, b3);finish = Min(e1, e2, e3);sum += (finish - start);b3 += t_mh;e3 += t_mh;}b2 += t_sh;e2 += t_sh;}b1 += t_sm;e1 += t_sm;}printf("%.3lf\n", sum / (12 * 60 * 60) * 100);}return 0;
}代码思路
-
常量:
sm、sh、mh分别代表三个假想的“指针”(小指针、特殊指针和中等指针)的速度(每分钟的度数)。t_sm、t_sh、t_mh分别表示这些“指针”完成一个完整周期所需的时间(以分钟计)。
-
输入处理:
- 程序读取一个值D,这个值代表任意两个“指针”要被认为是“接近”的最大角度距离。
- 如果D = 0,意味着“指针”必须完全重合,结果总是100%。
- 如果D = -1,则表示输入结束。
-
计算初始边界:
- 对于每个“指针”,它计算第一次它们会处于离起点DD度内的时刻(
b_sm、b_sh、b_mh)。 - 同样,它也计算第一次它们不会处于离起点DD度内的时刻(
e_sm、e_sh、e_mh)。
- 对于每个“指针”,它计算第一次它们会处于离起点DD度内的时刻(
-
查找重叠区间:
- 程序使用嵌套循环来遍历所有可能的时刻,这时所有的三个“指针”可以同时处于彼此DD度内。
- 根据当前迭代,更新边界(
b1、b2、b3)和端点(e1、e2、e3)。 - 它使用
Min和Max函数来找到所有“指针”都接近的区间的开始和结束。 - 它在
sum中累积这些区间的持续时间。
-
输出:处理完所有区间后,它计算出12小时总时段内所有“指针”处于DD度内的百分比时间。
高效地找到所有三个进程符合给定条件的重叠区间,即使它们有不同的速度和周期。
HDU1007——Quoit Design
题目描述
Problem - 1007

运行代码
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#define MAXX 1 << 30
#define MAXN 100010
using namespace std;
struct Point {double x, y;
};
Point p[MAXN];
int t[MAXN];
bool cmpX(const Point& a, const Point& b) {if (a.x == b.x) return a.y < b.y;return a.x < b.x;
}
bool cmpY(const int& a, const int& b) {return p[a].y < p[b].y;
}
double dist(Point a, Point b) {return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double findClosestPair(int left, int right) {double minDist = MAXX;if (left == right) return minDist;if (left + 1 == right) return dist(p[left], p[right]);int mid = (left + right) / 2;double leftMin = findClosestPair(left, mid);double rightMin = findClosestPair(mid + 1, right);minDist = min(leftMin, rightMin);int cnt = 0;for (int i = left; i <= right; i++) {if (fabs(p[i].x - p[mid].x) < minDist) {t[cnt++] = i;}}sort(t, t + cnt, cmpY);for (int i = 0; i < cnt; i++) {for (int j = i + 1; j < cnt && p[t[j]].y - p[t[i]].y < minDist; j++) {double d = dist(p[t[i]], p[t[j]]);minDist = min(minDist, d);}}return minDist;
}
int main() {int n;while (scanf("%d", &n) && n) {for (int i = 0; i < n; i++) {scanf("%lf%lf", &p[i].x, &p[i].y);}sort(p, p + n, cmpX);double r = findClosestPair(0, n - 1) / 2.0;printf("%.2lf\n", r);}return 0;
}代码思路
寻找二维平面上的最近点对。其主要思想是使用分治算法(Divide and Conquer)来解决,具体步骤如下:
-
定义结构体
Point存储每个点的坐标。 -
比较函数
cmpX和cmpY分别用于按照 x 坐标和 y 坐标排序点。 -
距离函数
dist计算两点之间的欧几里得距离。 -
递归函数
findClosestPair是核心部分,它接收左边界和右边界作为参数,表示要处理的点集范围。- 如果范围内只有一个点或没有点,返回一个很大的值
MAXX表示没有距离可言。 - 如果范围内正好有两个点,直接计算并返回这两个点的距离。
- 否则,将点集分为左右两半,递归地在两边找到最小距离。
- 然后,检查中线两侧的点是否包含更近的点对。为此,收集所有与中线距离小于目前最小距离的点,并按 y 坐标排序。
- 在这个已排序的子集中,检查每一对相邻点的 y 坐标差小于目前最小距离的点对,计算它们之间的距离,并更新最小距离。
- 如果范围内只有一个点或没有点,返回一个很大的值
-
主函数
main读取点集数量n和每个点的坐标,然后调用findClosestPair函数,最后输出最近点对之间距离的一半(题目可能要求输出半径,即最近点对距离的一半),保留两位小数。
这种方法的时间复杂度为 O(n log n),其中 n 是点的数量。这是因为每次递归调用处理一半的点,同时还需要对子集进行排序。空间复杂度为 O(n),因为需要额外的空间存储排序后的点和临时数组。
相关文章:

HDU1005——Number Sequence,HDU1006——Tick and Tick,HDU1007——Quoit Design
目录 HDU1005——Number Sequence 题目描述 超时代码 代码思路 正确代码 代码思路 HDU1006——Tick and Tick 题目描述 运行代码 代码思路 HDU1007——Quoit Design 题目描述 运行代码 代码思路 HDU1005——Number Sequence 题目描述 Problem - 1005 超时代码…...

uniapp form表单校验
公司的一个老项目,又要重新上架,uniapp一套代码,打包生成iOS端发布到App Store,安卓端发布到腾讯应用宝、OPPO、小米、华为、vivo,安卓各大应用市场上架要求不一样,可真麻烦啊 光一个表单校验,…...

构建RSS订阅机器人:观察者模式的实践与创新
在信息爆炸的时代,如何高效地获取和处理信息成为了一个重要的问题。RSS订阅机器人作为一种自动化工具,能够帮助我们从海量信息中筛选出我们感兴趣的内容。 一、RSS 是什么?观察者模式又是什么? RSS订阅机器人是一种能够自动订阅…...

芯片基础 | `wire`类型引发的学习
在Verilog中,wire类型是一种用于连接模块内部或模块之间的信号的数据类型。wire类型用于表示硬件中的物理连线,它可以传输任何类型的值(如0、1、高阻态z等),但它在任何给定的时间点上只能有一个确定的值。 wire类型通…...
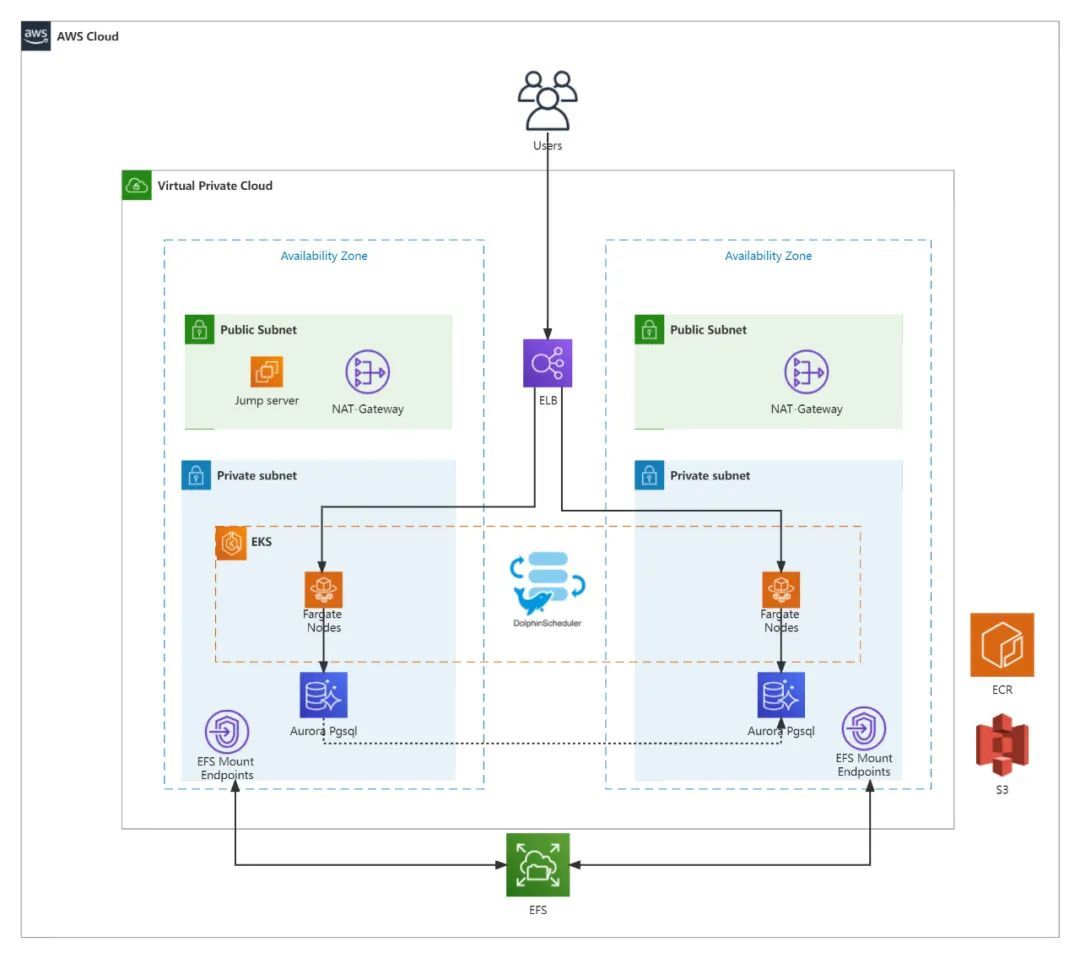
如何在AWS上构建Apache DolphinScheduler
引言 随着云计算技术的发展,Amazon Web Services (AWS) 作为一个开放的平台,一直在帮助开发者更好的在云上构建和使用开源软件,同时也与开源社区紧密合作,推动开源项目的发展。 本文主要探讨2024年值得关注的一些开源软件及其在…...

Quartus II 13.1添加新的FPGA器件库
最近需要用到Altera的一款MAX II 系列EPM240的FPGA芯片,所以需要给我的Quartus II 13.1添加新的器件库,在此记录一下过程。 1 下载所需的期间库 进入Inter官网,(Altera已经被Inter收购)https://www.intel.cn/content…...
)
【html】html的基础知识(面试重点)
一、如何理解HTML语义化 1、思考 A、在没有任何样式的前提下,将代码在浏览器打开,也能够结构清晰的展示出来。标题是标题、段落是段落、列表是列表。 B、便于搜索引擎优化。 2、参考答案 A、让人更容易读懂(增加代码可读性)。 B、…...

Java 网络编程(TCP编程 和 UDP编程)
1. Java 网络编程(TCP编程 和 UDP编程) 文章目录 1. Java 网络编程(TCP编程 和 UDP编程)2. 网络编程的概念3. IP 地址3.1 IP地址相关的:域名与DNS 4. 端口号(port)5. 通信协议5.1 通信协议相关的…...

STM32 | 看门狗+RTC源码解析
点击上方"蓝字"关注我们 作业 1、使用基本定时7,完成一个定时喂狗的程序 01、上节回顾 STM32 | 独立看门狗+RTC时间(第八天)02、定时器头文件 #ifndef __TIM_H#define __TIM_H#include "stm32f4xx.h"void Tim3_Init(void);void Tim7_Init(void);…...

filebeat,kafka,clickhouse,ClickVisual搭建轻量级日志平台
springboot集成链路追踪 springboot版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.3</version><relativePath/> <!-- lookup parent from…...

Django实战项目之进销存数据分析报表——第一天:Anaconda 环境搭建
引言 Anaconda是一个流行的Python和R语言的发行版,它包含了大量预安装的数据科学、机器学习库和科学计算工具。使用Anaconda可以轻松地创建隔离的环境,每个环境都可以有自己的一套库和Python版本,非常适合多项目开发。本文将指导你如何安装A…...

Linux部署Prometheus+Grafana
【Linux】PrometheusGrafana 一、Prometheus(普罗米修斯)1、Prometheus简述2、Prometheus特点3、Prometheus生态组件4、Prometheus工作原理 二、部署Prometheus1、系统架构2、部署Prometheus3、修改配置文件4、配置系统启动文件 三、部署 Node Exporter …...

【视频讲解】神经网络、Lasso回归、线性回归、随机森林、ARIMA股票价格时间序列预测|附代码数据
全文链接:https://tecdat.cn/?p37019 分析师:Haopeng Li 随着我国股票市场规模的不断扩大、制度的不断完善,它在金融市场中也成为了越来越不可或缺的一部分。 【视频讲解】神经网络、Lasso回归、线性回归、随机森林、ARIMA股票价格时间序列…...

低代码前端框架Amis全面教程
什么是Amis? 1.1 Amis的基本概念 Amis是一个基于JSON配置的前端低代码框架,由百度开源。它允许开发者通过简单的JSON配置文件来生成复杂的后台管理页面,从而大大减少了前端开发的工作量。Amis的核心理念是通过配置而非编码来实现页面的构建…...

Windows 如何安装和卸载 OneDrive?具体方法总结
卸载 OneDrive 有人想问 OneDrive 可以卸载吗?如果你不使用当然可以卸载,下面是安装和卸载 OneDrive 中的卸载应用具体操作步骤: 卸载 OneDrive 我们可以从设置面板中的应用选项进行卸载,打开设置面板之后选择应用,然…...

c# .net core中间件,生命周期
某些模块和处理程序具有存储在 Web.config 中的配置选项。但是在 ASP.NET Core 中,使用新配置模型取代了 Web.config。 HTTP 模块和处理程序如何工作 官网地址: 将 HTTP 处理程序和模块迁移到 ASP.NET Core 中间件 | Microsoft Learn 处理程序是…...
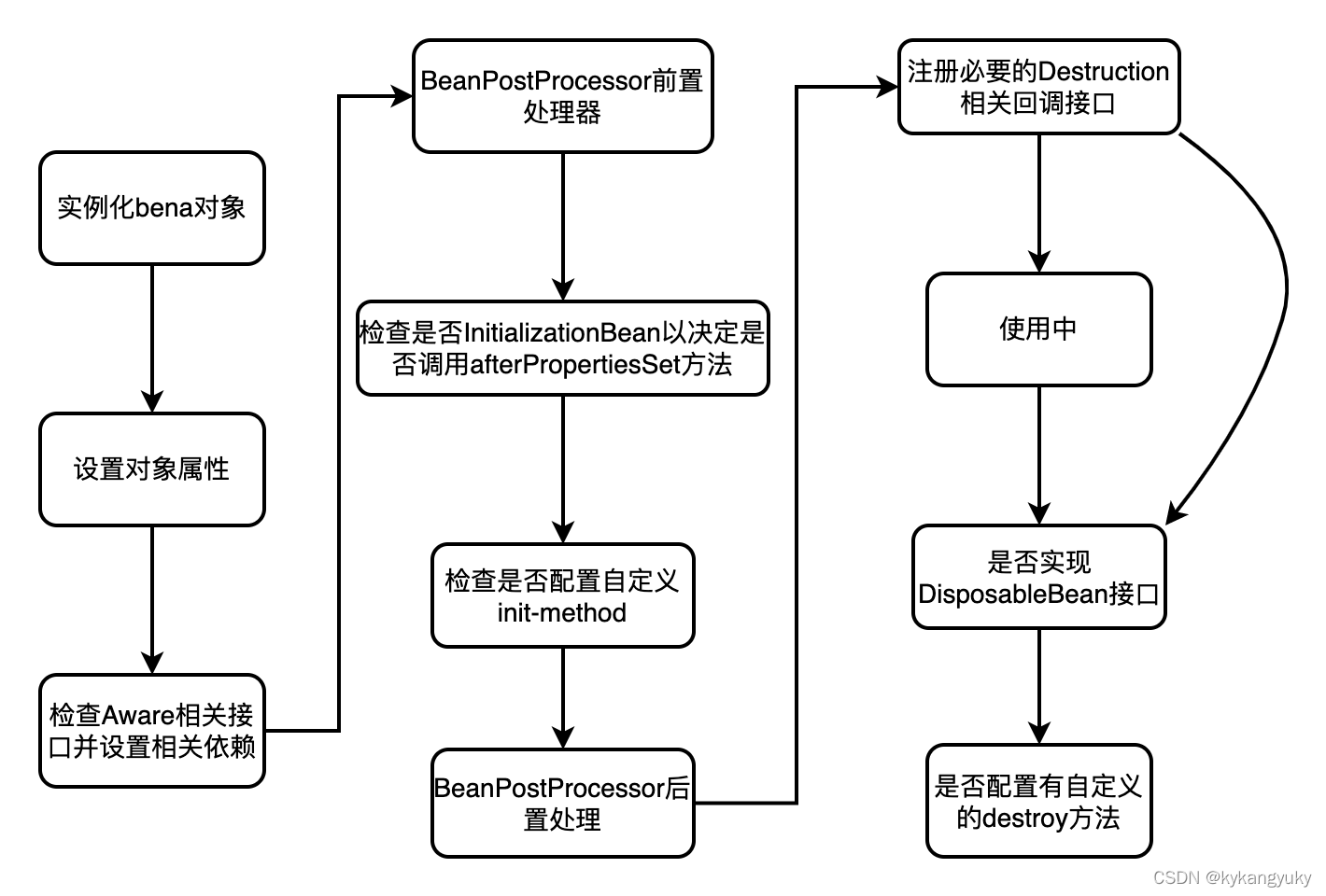
Spring后端框架复习总结
之前写的博客太杂,最近想把后端框架的知识点再系统的过一遍,主要是Spring Boot和Mybatis相关,带着自己的理解使用简短的话把一些问题总结一下,尤其是开发中和面试中的高频问题,基础知识点可以参考之前写java后端专栏,这篇不再赘述。 目录 Spring什么是AOP?底层原理?事务…...

基于Llama Index构建RAG应用
前言 Hello,大家好,我是GISer Liu😁,一名热爱AI技术的GIS开发者,本文参与活动是2024 DataWhale AI夏令营;😲 在本文中作者将通过: Gradio、Streamlit和LlamaIndex介绍 LlamaIndex 构…...

SSLRec代码分析
文章目录 encoder-models-general_cfautocf.py data_utilsdata_handler_general_cf.py输入输出说明使用方法 trainertuner.py encoder-models-general_cf autocf.py import torch as t # 导入PyTorch并重命名为t from torch import nn # 从PyTorch导入神经网络模块 import …...
(2))
第四节shell条件测试(1)(2)
一,命令执行结果判定 &&在命令执行后如果没有任何报错时会执行符号后面的动作 ||在命令执行后如果命令有报错会执行符号后的动作 示例: vim lee.sh #!/bin/bash ls /mnt/file &> /dev/null &&{echo /mnt/filr is not existecho no }||{echo /mnt/fi…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
