人工智能算法工程师(中级)课程14-神经网络的优化与设计之拟合问题及优化与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程14-神经网络的优化与设计之拟合问题及优化与代码详解。在机器学习和深度学习领域,模型的训练目标是找到一组参数,使得模型能够从训练数据中学习到有用的模式,并对未知数据做出准确预测。这一过程涉及到解决两种主要的拟合问题:欠拟合(Underfitting)和过拟合(Overfitting)。
文章目录
- 一、拟合问题概述
- 欠拟合现象
- 过拟合现象
- 解决策略
- 二、正则化方法
- 1. L1正则化
- 2. L2正则化
- 三、正则化参数的更新
- 四、Dropout
- 五、代码实现
一、拟合问题概述
在机器学习领域,拟合问题是指通过训练数据找到最佳模型参数,使得模型在未知数据上的表现尽可能好。拟合问题主要包括欠拟合和过拟合两种现象。
欠拟合现象
定义:欠拟合指的是机器学习模型在训练集上的表现不佳,无法充分学习到数据的内在规律,导致模型的预测能力低下。这就好比一个学生在考试中,由于知识掌握不牢固,对已知题目的解答都做不好,更不用说应对新题目了。
原因分析:
模型复杂度低:如果模型太简单,如用线性模型去拟合非线性的数据分布,那么模型就无法捕捉到数据中的复杂模式,就像用直尺去测量曲线长度一样,永远无法得到准确的结果。
训练数据不足:模型需要足够的数据来学习和概括数据的特性。如果数据量太少,模型可能没有机会接触到数据的全貌,就像从一本书中只读了几页就想理解整本书的内容一样困难。
特征选择不当:如果使用的特征与目标预测无关或相关性弱,模型就难以从中学习到有效的信息,相当于在解决问题时选择了错误的工具。
过拟合现象
定义:过拟合是指模型在训练数据上表现得过于出色,以至于对训练数据中的噪声或偶然性细节也进行了学习,这导致模型在面对未见过的数据时,泛化能力下降。这就像一个学生过分依赖于记忆特定的例题,而没有真正理解背后的原理,因此在遇到稍微变化的问题时就束手无策。
原因分析:
模型复杂度过高:如果模型过于复杂,如高阶多项式回归,它可能会过度适应训练数据中的每一个细节,包括噪声和异常值,而不是学习数据的普遍规律。
训练数据包含噪声:现实世界的数据往往带有噪声,如果模型试图学习这些噪声,就会导致过拟合。这类似于试图从嘈杂的环境中听清对话,噪声会干扰对真实信息的理解。
训练数据量不足:即使模型复杂度适中,但如果训练数据量不够,模型仍然可能过拟合。这是因为数据量不足时,模型可能会把偶然出现的模式误认为是普遍规律。
解决策略
增加模型复杂度:对于欠拟合,可以通过增加模型复杂度来提升模型的学习能力,如使用更高阶的多项式或更复杂的神经网络结构。
增加训练数据量:无论是欠拟合还是过拟合,增加训练数据量都能帮助模型更好地学习数据的分布,提高泛化能力。
特征工程:优化特征选择,确保模型能够基于有意义的特征进行学习。
正则化:使用L1或L2正则化等技术来限制模型复杂度,防止过拟合。
交叉验证:通过交叉验证来评估模型的泛化能力,确保模型不仅在训练数据上表现好,也能在未见数据上给出准确预测。
早停法:在训练过程中监控验证集的性能,一旦发现验证集上的性能不再提升,就停止训练,避免过拟合。

二、正则化方法
为了解决过拟合问题,通常采用正则化方法对模型进行约束。常见的正则化方法有L1正则化和L2正则化。
1. L1正则化
L1正则化的目标函数为:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + α ∑ j = 1 n ∣ θ j ∣ J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \alpha\sum_{j=1}^{n}|\theta_j| J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+αj=1∑n∣θj∣
其中,第一项为损失函数,第二项为L1正则化项, α \alpha α为惩罚系数, θ j \theta_j θj为模型参数。
2. L2正则化
L2正则化的目标函数为:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + α 2 ∑ j = 1 n θ j 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \frac{\alpha}{2}\sum_{j=1}^{n}\theta_j^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+2αj=1∑nθj2
其中,第一项为损失函数,第二项为L2正则化项, α \alpha α为惩罚系数, θ j \theta_j θj为模型参数。
三、正则化参数的更新
在优化目标函数时,我们需要对正则化参数进行更新。以下为L2正则化的参数更新公式:
θ j : = θ j − α ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ θ j ) \theta_j := \theta_j - \alpha\left(\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)} + \lambda\theta_j\right) θj:=θj−α(m1i=1∑m(hθ(x(i))−y(i))xj(i)+λθj)
其中, λ = α m \lambda = \frac{\alpha}{m} λ=mα为正则化参数。

四、Dropout
Dropout是一种有效的正则化方法,通过在训练过程中随机丢弃部分神经元,来减少模型对特定训练样本的依赖。以下是Dropout的实现步骤:
(1)在训练过程中,按照一定概率随机丢弃神经元;
(2)在测试过程中,将所有神经元的输出乘以概率因子。
五、代码实现
以下是基于PyTorch的拟合问题及优化代码实现:
import torch
import torch.nn as nn
import torch.optim as optim
# 定义模型
class LinearRegression(nn.Module):def __init__(self, input_dim, output_dim):super(LinearRegression, self).__init__()self.linear = nn.Linear(input_dim, output_dim)def forward(self, x):return self.linear(x)
# 生成数据
x = torch.randn(100, 1)
y = 3 * x + 2 + torch.randn(100, 1)
# 实例化模型
model = LinearRegression(1, 1)
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=0.01) # L2正则化
# 训练模型
num_epochs = 100
for epoch in range(num_epochs):model.train()optimizer.zero_grad()outputs = model(x)loss = criterion(outputs, y)loss.backward()optimizer.step()if (epoch+1) % 10 == 0:print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item()}')
# 测试模型
model.eval()
with torch.no_grad():predicted = model(x).detach().numpy()print(f'预测值:{predicted}')
通过本文的介绍,相信大家对拟合问题及优化方法有了更深入的了解。在实际应用中,可根据数据特点选择合适的正则化方法,以提高模型的泛化能力。
相关文章:

人工智能算法工程师(中级)课程14-神经网络的优化与设计之拟合问题及优化与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程14-神经网络的优化与设计之拟合问题及优化与代码详解。在机器学习和深度学习领域,模型的训练目标是找到一组参数,使得模型能够从训练数据中学习到有用的模式&am…...

Java异常抛出与处理方法
在Java编程中,异常处理是一个非常重要的部分。通过正确的异常处理,我们可以提高程序的健壮性和可靠性,避免程序在运行过程中出现意外的崩溃。本文将详细讲述Java异常的抛出与处理方法,并通过示例代码进行说明。 一、Java异常的分类 Java中的异常体系结构可以分为三类: 检…...

兼容性测试主要有什么类型?
兼容性测试的类型 有两种类型的兼容性测试。这是一个快速细分。 1、前向兼容性测试 向前兼容性测试或向上兼容性测试可确保当前软件版本在相关组件(例如操作系统、浏览器和第三方库)的未来版本中保持功能。此类测试对于在系统升级期间保持稳定性和用户体验至关重要。 例如&…...

设计模式--组合模式
组合模式(Composite Pattern)详解 组合模式是一种结构型设计模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得用户对单个对象和组合对象的使用具有一致性。 适用场景 需要表示对象的部分-整体层次结构时&am…...

ArduPilot开源代码之AP_DAL_RangeFinder
ArduPilot开源代码之AP_DAL_RangeFinder 1. 源由2. 框架设计2.1 枚举 Status2.2 公有方法2.3 私有成员变量 3. 重要例程3.1 应用函数3.1.1 ground_clearance_cm_orient3.1.2 max_distance_cm_orient3.1.3 has_orientation3.1.4 get_backend 3.2 其他函数3.2.1 AP_DAL_RangeFind…...

SpringCloud教程 | 第九篇: 使用API Gateway
1、参考资料 SpringCloud基础篇-10-服务网关-Gateway_springcloud gateway-CSDN博客 2、先学习路由,参考了5.1 2.1、建了一个cloudGatewayDemo,这是用来配置网关的工程,配置如下: http://localhost:18080/aaa/name 该接口代码如…...

数据结构——hash(hashmap源码探究)
hash是什么? hash也称为散列,就是把任意长度的输入,通过散列算法,变成固定长度的输出,这个输出值就是散列值。 举例来说明一下什么是hash: 假设我们要把1~12存入到一个大小是5的hash表中,我们…...

国产麒麟、UOS在线打开pdf加盖印章
PageOffice支持两种电子印章方案,可实现对Word、Excel、PDF文档加盖PageOffice自带印章或ZoomSeal电子印章(全方位保护、防篡改、防伪造)。Word和Excel的盖章功能请参考:Word和Excel加盖印章和签字功能 (目前只支持win…...

破解反爬虫策略 /_guard/auto.js(二)实战
这次我们用上篇文章讲到的方法来真正破解一下反爬虫策略,这两个案例是两个不同的网站,一个用的是 /_guard/auto.js,另一个用的是/_guard/delay_jump.js。经过解析发现这两个网站用的反爬虫策略基本是一模一样,只不过在js混淆和生成…...

同样是人工智能 客户在哪儿AI和GPT等大模型有什么不同
书接上回。为了统一回答朋友们的疑惑,此前的两篇文章,着重讲述了客户在哪儿AI的企业全历史行为数据和企业信息查询平台上的数据的区别,以及客户在哪儿AI的ToB获客服务和AI外呼机器人的获客服务的不同。本期接着讲——客户在哪儿AI VS 大模型&…...

AES Android IOS H5 加密方案
前景: 1、本项目原有功能RSA客户端对敏感信息进行加密 2、本次漏洞说是服务端返回值有敏感信息,需要密文返回 3、最初只跟H5联调成功,后续APP联调失败(H5和APP的需求排期不一致),没关注到通用性 方案: 本次方案不…...

一文了解变阻器和电位器的定义、原理、应用及其对比
变阻器的定义 两端可变电阻器(称为变阻器)利用电阻来调节电流。电阻丝环绕在陶瓷或瓷器等绝缘芯上。当刮水器沿着电阻丝移动时,电路的有效电阻会发生变化。因此,它提供了精确的电流控制。调光器、电机速度控制器和加热元件使用变…...

WPF实现一个带旋转动画的菜单栏
WPF实现一个带旋转动画的菜单栏 一、创建WPF项目及文件1、创建项目2、创建文件夹及文件3、添加引用 二、代码实现2.ControlAttachProperty类 一、创建WPF项目及文件 1、创建项目 打开VS2022,创建一个WPF项目,如下所示 2、创建文件夹及文件 创建资源文件夹&…...

使用Dockerfile构建镜像
目录 1.使用Dockerfile构建tomcat镜像 1.1 通过ARG传参构建不同版本的tomcat 2.缩小镜像的体积大小 2.1 使用较小体积的基础镜像 2.2 多级构建减少体积 1.使用Dockerfile构建tomcat镜像 cd /opt mkdir tomcat cd tomcat/ 上传tomcat所需的依赖包 使用tar xf 解压三个压缩…...

概率论原理精解【3】
文章目录 向量值向量值函数导数对称矩阵定义性质例子应用 向量值理论基础定义性质应用示例 向量值函数的导数定义性质应用 向量值 向量值函数导数 D n ⊂ R n , 向量值函数 f : D n → R m D^n \subset R^n,向量值函数f:D^n\rightarrow R^m Dn⊂Rn,向量值函数f:Dn→Rm 1. 向量…...
)
[C/C++入门][循环]14、计算2的幂(2的n次方)
计算2的幂(即2的n次方)非常经典。你懂几种方法呢?很多人只会一种,我们来分析一下。 可以通过多种方式实现: 1、最简单的方法之一是使用位运算符<<,它本质上是在二进制表示下对2进行左移操作&#x…...

RPC与服务的注册发现
文章目录 1. 什么是远程过程调用(RPC)?2. RPC的流程3. RPC实践4. RPC与REST的区别4.1 RPC与REST的相似之处4.2 RPC与REST的架构原则4.3 RPC与REST的主要区别 5. RPC与服务发现5.1 以zookeeper为服务注册中心5.2 以etcd为服务注册中心 6. 小结参考 1. 什么是远程过程调用(RPC)?…...
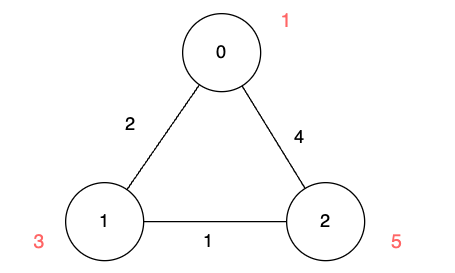
3112. 访问消失节点的最少时间 Medium
给你一个二维数组 edges 表示一个 n 个点的无向图,其中 edges[i] [ui, vi, lengthi] 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。 同时给你一个数组 disappear ,其中 disappear[i] 表示节点 i 从图中消失的时间点࿰…...

FastAPI 学习之路(五十二)WebSockets(八)接受/发送json格式消息
前面我们发送的大多数都是text类型的消息,对于text消息来说,后端处理出来要麻烦的多,那么我们可以不可以传递json格式的数据,对于前后端来说都比较友好,答案是肯定的,我们需要做下处理。 首先,…...

Go语言并发编程-案例_3
案例 并发目录大小统计 业务逻辑 统计目录的文件数量和大小(或其他信息)。示例输出: // 某个目录:2637 files 1149.87 MB 实现思路 给定一个或多个目录,并发的统计每个目录的size,最后累加到一起。 当…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
