算法复杂度<数据结构 C版>
什么是算法复杂度?
简单来说算法复杂度是用来衡量一个算法的优劣的,一个程序在运行时,对运行时间和运行空间有要求,即时间复杂度和空间复杂度。
目录
什么是算法复杂度?
大O的渐近表达式
时间复杂度示例
空间复杂度示例
常见复杂度对比:
大O的渐近表达式
时间复杂度,我们常常使用大O的渐近表示法
推导大O阶的规则:
●时间复杂度函数式T(N)中,只保留高阶项,去掉那些低阶项。
(因为当N不断变大时,低阶项对结果的影响越来越小,当N无穷大时,就可以忽略不计了)
●如果最高阶项存在且不是1,则去除这个项目的常数系数。
(因为当N不断变大,这个系数对结果的影响不断变小,当N无穷大时,其就可以忽略不计了)
●T(N)如果没有N相关的项目,只有常数项,那么就用常数1替代所有加法。
时间复杂度示例
1.
// 计算Func2的时间复杂度?
void Func2(int N)
{ int count = 0; //1次for (int k = 0; k < 2 * N ; ++ k) { ++count; //2*N次} int M = 10; while (M--) { ++count; //10次} printf("%d\n", count);
}得:T(N)=1+2*N+10
由第一条和第二条规则得到时间复杂度O(N).
2.
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{ int count = 0; for (int k = 0; k < M; ++ k) //M次{ ++count; } for (int k = 0; k < N ; ++ k) //N次{ ++count; } printf("%d\n", count);
}得:T(N)=M+N
由第一条规则或第二条规则得到时间复杂度O(N).
(因为使用N代表其中增长速度快的哪一项,则忽略掉增长速度慢的那一项,当M和N增长速度一样时为2N,则忽略系数)
3.
// 计算Func4的时间复杂度?
void Func4(int N)
{ int count = 0; for (int k = 0; k < 100; ++ k) //100次{ ++count; } printf("%d\n", count);
}得:T(N)=100
由第三条规则得到时间复杂度O(1).
4.
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character)
{const char* p_begin = s;while (*p_begin != character){if (*p_begin == '\0')return NULL;p_begin++;}return p_begin;
}①最好情况
str的第一个字符就等于character,得:T(N)=1,则时间复杂度为O(1).
②平均情况
要查找的字符在str的中间,得:T(N)=N/2,则时间复杂度为O(N).
③最差情况
要查找字符在str的末尾,得:T(N)=N,则时间复杂度为O(N).
一般的我们取最差情况来表示算法的时间复杂度
★某些算法存在分情况的时间复杂度
●最坏情况:任意输入规模的最大运行次数(上界).
●平均情况:任意输入规模的平均次数.
●最好情况:任意输入规模的最小次数(下界).
5.
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{ assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i-1] > a[i]) { Swap(&a[i-1], &a[i]); exchange = 1; } } if (exchange == 0) break; }
}通过上面的分析,我们可尝试求出三种情况:
最坏情况:倒序,O(N^2)
平均情况:平均情况,O(N^2)
最好情况:有序,O(N)
6.
void func5(int n)
{int cnt = 1;while (cnt < n){cnt *= 2;}
}分析得T(N)=log2n,即O(logn).
7.
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{ if(0 == N)return 1; return Fac(N-1)*N;
}时间复杂度:O(N).
空间复杂度示例
空间复杂度的表示也使用大O表达式。
1.
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{ assert(a); //1次for (size_t end = n; end > 0; --end) //一次{ int exchange = 0; //一次for (size_t i = 1; i < end; ++i) //一次{ if (a[i-1] > a[i]) { Swap(&a[i-1], &a[i]); exchange = 1; } } if (exchange == 0) break; }
}空间复杂度:O(1).
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{ if(N == 0) return 1; return Fac(N-1)*N;
}
开辟了N个函数栈帧,空间复杂度为O(N)
常见复杂度对比:


相关文章:

算法复杂度<数据结构 C版>
什么是算法复杂度? 简单来说算法复杂度是用来衡量一个算法的优劣的,一个程序在运行时,对运行时间和运行空间有要求,即时间复杂度和空间复杂度。 目录 什么是算法复杂度? 大O的渐近表达式 时间复杂度示例 空间复杂度…...

【XSS】
文章目录 0x01 简介0x02 XSS Payload用法XSS攻击平台及调试JavaScript 0x03 XSS绕过XSS漏洞防御策略 跨站脚本攻击,Cross Site Script。(重点在于脚本script) 有关XSS可以造成的 危害,见 0x02 XSS Payload用法 分类 反射型、存储…...
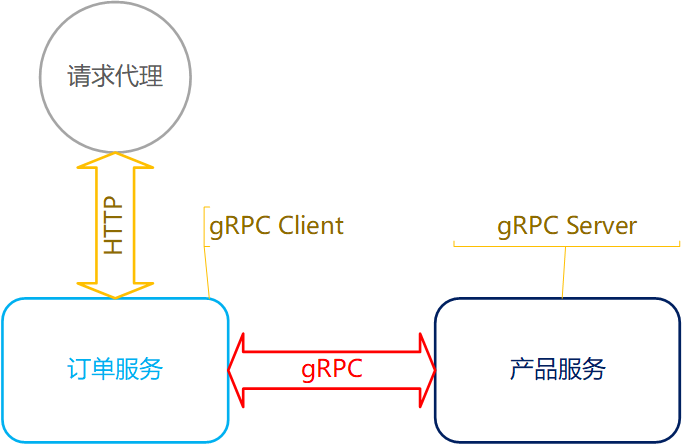
Go网络编程-RPC程序设计
gRPC 通信 RPC 介绍 RPC, Remote Procedure Call,远程过程调用。与 HTTP 一致,也是应用层协议。该协议的目标是实现:调用远程过程(方法、函数)就如调用本地方法一致。 如图所示: 说明: Servi…...

Linux 性能优化:轻松入门
文章目录 前言一、磁盘性能优化1、 磁盘 RAID 模式选择2、文件系统优化 二、优化 CPU1、性能监控 :2、进程优先级调整 :3、进程与 CPU 绑定 : 三、优化内存四、网络性能优化1、调整 TCP 缓冲区大小2、修改系统级别的文件描述符的数量3、调整 …...

C++相关概念和易错语法(22)(final、纯虚函数、继承多态难点)
1.final final在继承和多态中都可以使用,在继承中是指不想将自己被继承,在多态中是指不想该函数被重写,比较简单,下面是一些使用例子。 2.纯虚函数 当我们需要抽象一个类的时候,我们就需要用到纯虚函数。所谓抽象的类…...

状态管理的艺术:探索Flutter的Provider库
状态管理的艺术:探索Flutter的Provider库 前言 上一篇文章中,我们详细介绍了 Flutter 应用中的状态管理,以及 StatefulWidget 和 setState 的使用。 本篇我们继续介绍另一个实现状态管理的方式:Provider。 Provider优缺点 基…...

玩转HarmonyOS NEXT之IM应用首页布局
本文从目前流行的垂类市场中,选择即时通讯应用作为典型案例详细介绍HarmonyOS NEXT的各类布局在实际开发中的综合应用。即时通讯应用的核心功能为用户交互,主要包含对话聊天、通讯录,社交圈等交互功能。 应用首页 创建一个包含一列的栅格布…...
GPT-4o大语言模型优化、本地私有化部署、从0-1搭建、智能体构建
原文链接:GPT-4o大语言模型优化、本地私有化部署、从0-1搭建、智能体构建https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247608565&idx3&snd4e9d447efd82e8dd8192f7573886dab&chksmfa826912cdf5e00414e01626b52bab83a96199a6bf69cbbef7f7fe…...
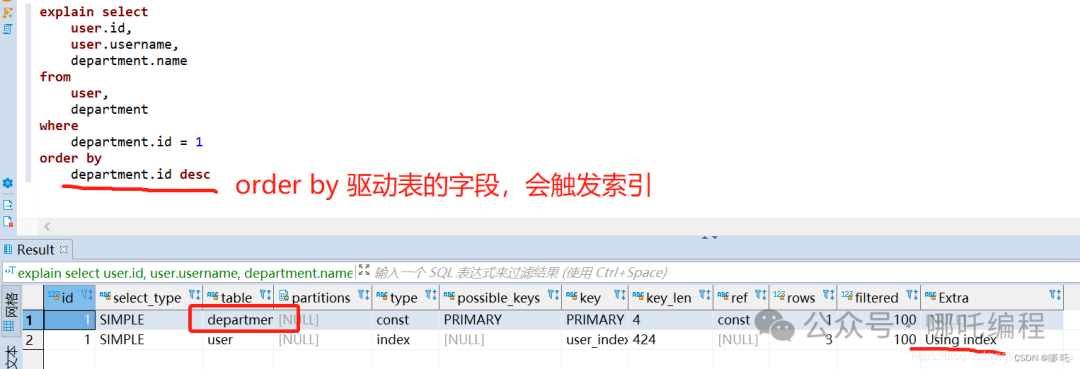
记录些MySQL题集(4)
1、数据库的三范式是什么? 第一范式:列不可再分 第二范式:在第一范式的基础上,要求数据库表中的所有非主键列完全依赖于主键,而不是仅依赖于主键的一部分 第三范式:满足第二范式的基础上,所有…...
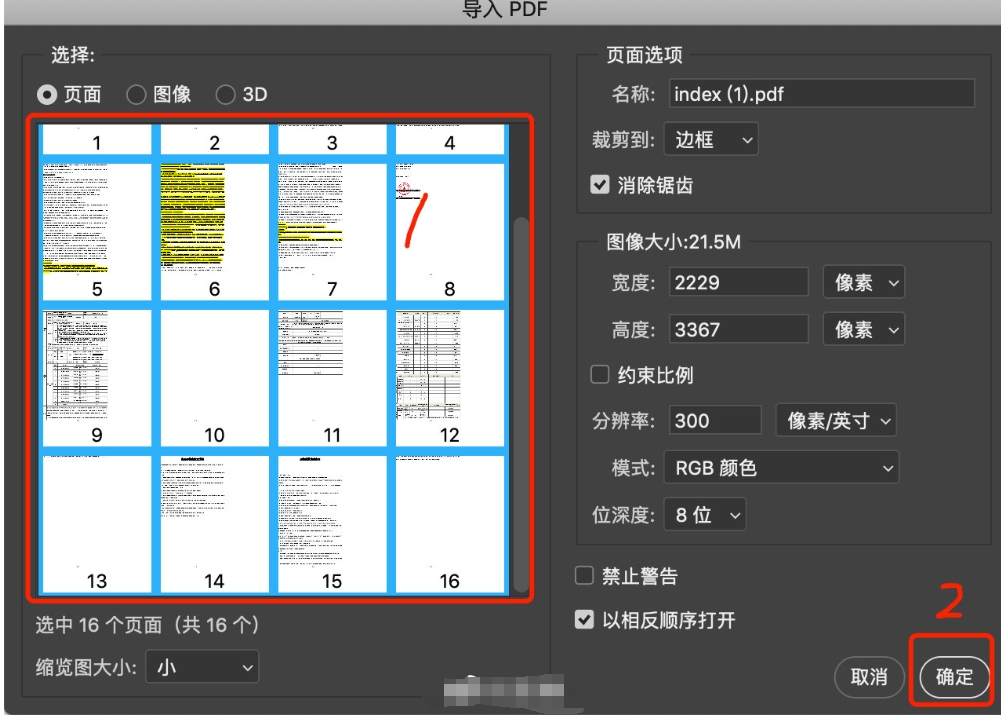
pdf提取其中一页怎么操作?提取PDF其中一页的方法
pdf提取其中一页怎么操作?需要从一个PDF文件中提取特定页码的操作通常是在处理文档时常见的需求。这种操作允许用户选择性地获取所需的信息,而不必操作整个文档。通过选择性提取页面,你可以更高效地管理和利用PDF文件的内容,无论是…...

godot使用ws
go服务端 package mainimport ("encoding/json""fmt""github.com/gorilla/websocket""net/http" )var upgrader websocket.Upgrader{ReadBufferSize: 1024,WriteBufferSize: 1024, }// 处理函数 func handleWebSocket(w http.Respo…...

Windows FFmpeg 开发环境搭建
FFmpeg 开发环境搭建 FFmpeg命令行环境搭建使用FFmpeg官方编译的库Windows编译FFmpeg1. 下载[msys2](https://www.msys2.org/#installation)2. 安装完成之后,将安装⽬录下的msys2_shell.cmd中注释掉的 rem set3. 修改pacman 镜像源并安装依赖4. 下载并编译源码 FFmpeg命令行环境…...

链路聚合概述
目录 技术背景: 基本概念: 链路聚合的工作模式: 简介: 1)Manual Load-balance(手动负载分担) 简介: 配置实施: 2)LACP(链路聚合控制协议ÿ…...

【链表】算法题(二) ----- 力扣/牛客
一、链表的回文结构 思路: 找到链表的中间节点,然后逆置链表的后半部分,再一一遍历链表的前半部分和后半部分,判断是是否为回文结构。 快慢指针找到链表的中间节点 slow指针指向的就是中间节点 逆置链表后半部分 逆置链表后半部分…...

合成复用原则
合成复用原则 (Composite Reuse Principle, CRP) 合成复用原则(Composite Reuse Principle, CRP),也被称为组合/聚合复用原则,是面向对象设计中的一条重要原则。它的核心思想是:优先使用对象组合/聚合,而不…...

安卓自带camera hal3 实例README.md翻译
最近,遇到一个这样的问题,临时了解下这个驱动实现架构和特点,翻译如下 V4L2相机HALv3 camera.v4l2库使用视频Linux 2(V4L2)接口实现了camera HAL v3。这使得它在理论上可以与各种设备配合使用,尽管V4L2的…...

ActiViz实战:ActiViz中的自己实现鼠标双击事件
文章目录 1、添加鼠标事件2、网上实现双击事件的方式3、增加双击的时间限制4、补充说明1、添加鼠标事件 已知在C#中观察者/命令模式会报错,正常添加鼠标事件如下: private void VtkInteractorStyleTest() {vtkInteractorStyle style = vtkInteractorStyle.New();style.LeftB…...

Linux-交换空间(Swap)管理
引入概念 在计算机中,硬盘的容量一般比内存大,内存(4GB 8GB 16GB 32GB 64GB…),硬盘(512GB 1T 2T…)。 冯诺依曼的现代计算机结构体系里面的存储器就是内存 内存是一种易失性存储器,…...

扫描某个网段下存活的IP:fping
前言: 之前用arp统计过某网段下的ip,但是有可能统计不全。网络管理平台又不允许登录。想要知道当前的ip占用情况,可以使用fping fping命令类似于ping,但比ping更强大。与ping需要等待某一主机连接超时或发回反馈信息不同&#x…...

【深度学习】PyTorch框架(3):优化与初始化
1.引言 在本文中,我们将探讨神经网络的优化与初始化技术。随着神经网络深度的增加,我们会遇到多种挑战。最关键的是确保网络中梯度流动的稳定性,否则可能会遭遇梯度消失或梯度爆炸的问题。因此,我们将深入探讨以下两个核心概念&a…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
