【Matlab算法】粒子群算法求解一维非线性函数问题(附MATLAB代码)
MATLAB求解一维非线性函数问题
- 前言
- 正文
- 函数实现(可视化处理)
- 可视化结果
前言
一维非线性函数是指函数的自变量和因变量都是一维实数,而且函数的形式是非线性的,也就是不符合线性函数的形式。在一维非线性函数中,自变量和因变量之间的关系通常是曲线状的,而不是直线状的。这种函数形式很常见,可以描述很多实际问题,如物理学、工程学、生物学等领域的各种现象和过程。常见的一维非线性函数包括二次函数、指数函数、对数函数、三角函数等。这些函数形式都不是线性的,其函数值与自变量之间的关系并不满足线性关系,因此需要使用不同的数学方法来求解最优解。
下面几个常见的一维非线性函数的例子:
幂函数:y=x2y=x^2y=x2、y=x3y=x^3y=x3、y=x4y=x^4y=x4等;
指数函数:y=exy=e^xy=ex、y=2xy=2^xy=2x、y=10xy=10^xy=10x等;
对数函数:y=ln(x)y=\ln(x)y=ln(x)、y=log2(x)y=\log_2(x)y=log2(x)、y=log10(x)y=\log_{10}(x)y=log10(x)等;
三角函数:y=sin(x)y=\sin(x)y=sin(x)、y=cos(x)y=\cos(x)y=cos(x)、y=tan(x)y=\tan(x)y=tan(x)等;
双曲函数:y=sin(x)y=\sin(x)y=sin(x)、y=cos(x)y=\cos(x)y=cos(x)、y=tan(x)y=\tan(x)y=tan(x)等;
逻辑斯蒂函数:y=11+e−xy = \frac{1}{1+e^{-x}}y=1+e−x1,常用于分类问题中的概率计算。
这些非线性函数的特点是函数图像不是一条直线,而是具有弯曲或曲线变化的形状,其导数也不是常数而是变化的。在优化问题中,非线性函数的优化往往比线性函数更加复杂和困难。
粒子群算法(Particle Swarm Optimization,PSO) 是一种启发式优化算法,它源于对鸟群捕食行为的研究。在粒子群算法中,被优化的问题被视为一个多维空间中的目标函数,算法通过模拟群体中每个粒子在空间中的搜索行为来寻找目标函数的全局最优解。
每个粒子在搜索空间中的位置表示一个潜在解,其速度表示了搜索方向和步长。每个粒子具有一个适应度值,该适应度值根据目标函数的表现来计算。粒子群算法通过协同粒子的行为来优化目标函数。粒子的速度和位置在每个迭代中被更新,使其朝着群体中的最佳位置和全局最佳位置移动。
粒子群算法的运行过程如下:
- 初始化粒子群,包括每个粒子的初始位置和速度,并设置全局最佳位置和全局最佳适应度值为初始值。
- 计算每个粒子的适应度值,更新全局最佳位置和全局最佳适应度值。
- 更新每个粒子的速度和位置,根据每个粒子当前位置与全局最佳位置之间的差异来调整速度和位置。
- 重复步骤
2和3,直到达到指定的停止准则,如达到最大迭代次数或满足收敛要求。
在实践中,粒子群算法经常与其他优化算法结合使用,例如遗传算法、模拟退火等。这些算法的组合可以提高搜索效率和准确性,从而提高优化问题的解决效率。
正文
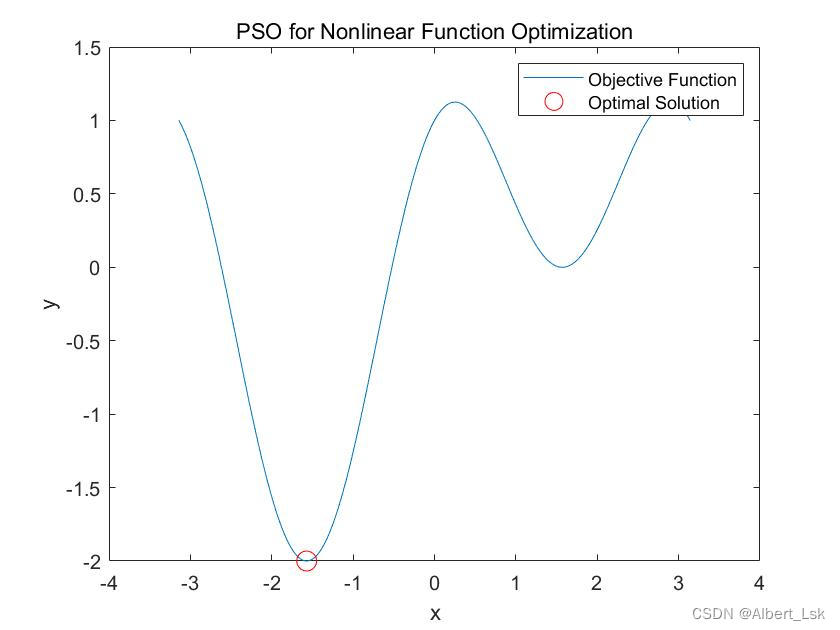
优化如下的三角函数:y=sin(x)+cos(2x)y=\sin(x)+\cos(2x)y=sin(x)+cos(2x)
其中,xxx 为变量,范围为 [−π,π][-\pi, \pi][−π,π]。
具体优化步骤如下:
- 初始化粒子群:随机生成一些粒子的位置和速度。
- 计算每个粒子的适应度:根据粒子的位置计算目标函数值。
- 更新全局最优解和个体最优解:记录历史最优解,并更新全局最优解和个体最优解。
- 更新粒子的速度和位置:根据全局最优解和个体最优解来更新粒子的速度和位置。
- 检查终止条件:检查是否满足终止条件,如果不满足则返回第3步。
在实际的实现中,我们需要选择合适的参数,如粒子数、迭代次数、惯性权重、加速度系数等,以及相应的初始值。此外,我们还需要考虑如何处理边界问题,如何控制算法的收敛速度等。
最后,通过绘制目标函数的图像来观察算法的优化效果,即目标函数值随着迭代次数的变化情况。
函数实现(可视化处理)
%%
clear
close all
warning off
clc
%% 调用粒子群算法求解
x_min = -pi;
x_max = pi;
n_pop = 50;
n_iter = 100;
w = 0.8;
c1 = 1.5;
c2 = 1.5;
[gbest, gbest_val] = pso(@objfun, x_min, x_max, n_pop, n_iter, w, c1, c2);% 输出结果
fprintf('最优解:x = %f,最优值:%f\n', gbest, gbest_val);% 可视化处理
x = linspace(-pi, pi, 1000);
y = sin(x) + cos(2*x);
plot(x, y);
hold on;
plot(gbest, gbest_val, 'ro', 'MarkerSize', 10);
title('PSO for Nonlinear Function Optimization');
xlabel('x');
ylabel('y');
legend('Objective Function', 'Optimal Solution');
hold off;% 目标函数
function y = objfun(x)y = sin(x) + cos(2*x);
end% 粒子群算法
function [gbest, gbest_val] = pso(objfun, x_min, x_max, n_pop, n_iter, w, c1, c2)% 参数设置x_range = x_max - x_min;v_min = -x_range;v_max = x_range;% 初始化粒子pop = x_min + rand(n_pop, 1) * x_range;v = v_min + rand(n_pop, 1) * (v_max - v_min);pbest = pop;pbest_val = objfun(pop);[gbest_val, gbest_idx] = min(pbest_val);gbest = pbest(gbest_idx);% 迭代for i = 1:n_iter% 更新速度和位置r1 = rand(n_pop, 1);r2 = rand(n_pop, 1);v = w*v + c1*r1.*(pbest-pop) + c2*r2.*(gbest-pop);pop = pop + v;% 边界处理pop(pop < x_min) = x_min;pop(pop > x_max) = x_max;% 更新个体历史最优和全局历史最优pbest_val_new = objfun(pop);pbest_update_idx = pbest_val_new < pbest_val;pbest(pbest_update_idx) = pop(pbest_update_idx);pbest_val(pbest_update_idx) = pbest_val_new(pbest_update_idx);[gbest_val_new, gbest_idx_new] = min(pbest_val);if gbest_val_new < gbest_valgbest = pbest(gbest_idx_new);gbest_val = gbest_val_new;endend
end可视化结果
相关文章:

【Matlab算法】粒子群算法求解一维非线性函数问题(附MATLAB代码)
MATLAB求解一维非线性函数问题前言正文函数实现(可视化处理)可视化结果前言 一维非线性函数是指函数的自变量和因变量都是一维实数,而且函数的形式是非线性的,也就是不符合线性函数的形式。在一维非线性函数中,自变量…...

2023 最新发布超全的 Java 面试八股文,整整 1000道面试题,太全了
作为一名优秀的程序员,技术面试都是不可避免的一个环节,一般技术面试官都会通过自己的方式去考察程序员的技术功底与基础理论知识。 2023 年的互联网行业竞争越来越严峻,面试也是越来越难,很多粉丝朋友私信希望我出一篇面试专题或…...

产品经理面经|当面试官问你还有什么问题?
相信很多产品经理在跳槽面试的时候,在面试尾声都会遇到这样的环节,面试官会问你有什么问题要问的,一般来说大家都能随时随地甩出几个问题来化解,但其实在这个环节对于应聘者来说也是一个很好的机会来展现自己的能力,甚…...

单链表的基本操作
目录 一.链表的基本概念和结构 二.链表的分类 三.单链表的基本操作 1.创建一个节点 2.打印 3.尾插 4.头插 5.尾删 6.头删 7.查找 8.指定位置插入 9.指定位置删除 10.销毁 一.链表的基本概念和结构 概念:链表是一种物理存储结构上非连续、非顺序的存储结…...
)
【微信小程序-原生开发】系列教程目录(已完结)
01-注册登录账号,获取 AppID、下载安装开发工具、创建项目、上传体验 https://sunshinehu.blog.csdn.net/article/details/128663679 02-添加全局页面配置、页面、底部导航 https://sunshinehu.blog.csdn.net/article/details/128705866 03-自定义底部导航&#x…...

JavaEE--Thread 类的基本用法(不看你会后悔的嘿嘿)
Thread类是JVM用来管理线程的一个类,换句话说,每个线程都唯一对应着一个Thread对象. 因此,认识和掌握Thread类弥足重要. 本文将从 线程创建线程中断线程等待线程休眠获取线程实例 等方面来进行具体说明. 1)线程创建 方法1:通过创建Thread类的子类并重写run () 方法 class M…...

MySQL数据库基本使用(二)-------数据库及表的增删改查及字符集修改
1.MySQL数据库的使用演示 1.1创建自己的数据库 命令格式如下(创建的数据库名称不能与已经存在的数据库重名): mysql> create database 数据库名;例如: mysql> create database atguigudb; #创建atguigudb数据库…...
)
互联网摸鱼日报(2023-03-17)
互联网摸鱼日报(2023-03-17) InfoQ 热门话题 开源新生代的成长之路:从校园到开源,需要迈过哪些挑战? 从 Clickhouse 到 Apache Doris,慧策电商 SaaS 高并发数据服务的改造实践 刚刚,百度文心…...
【前后端】低代码平台Jeecg-Boot 3.2宝塔云服务器部署流程
1 后端 部署流程 修改配置文件 更改数据库、redis的配置。 在system子模块中的target文件夹下生成 jar 包jeecg-boot-module-system-3.2.0.jar。 复制到云服务器 生成数据库 在这里插入图片描述 使用命令运行后端程序 java -jar ./jeecg-boot-module-system-3.2.0.jar宝…...

leetcode todolist
数组 数组的改变、移动 453. 最小移动次数使数组元素相等 665. 非递减数列 283. 移动零 数组的旋转 189. 旋转数组 396. 旋转函数 统计数组中的元素 645. 错误的集合 697. 数组的度 448. 找到所有数组中消失的数字 442. 数组中重复的数据 41. 缺失的第一个正数 数…...

改进YOLO系列 | CVPR2023最新 PConv | 提供 YOLOv5 / YOLOv7 / YOLOv7-tiny 模型 YAML 文件
DWConv是Conv的一种流行变体,已被广泛用作许多神经网络的关键构建块。对于输入 I ∈ R c h w I \in R^{c \times h \times w} I∈...
像ChatGPT玩转Excel数据
1.引言 最近ChatGPT的出现,把人工智能又带起了一波浪潮。机器人能否替代人类又成了最近热门的话题。 今天我们推荐的一个玩法和ChatGPT有点不一样。我们的课题是“让用户可以使用自然语言从Excel查询到自己想要的数据”。 要让自然语言可以从Excel中查数据&#…...

云原生之docker容器监控详解(cAdvisor、node exporter、prometheus)
docker容器监控一、前言二、cAdvisor2.1、安装cAdvisor2.2、使用Prometheus监控cAdvisor2.3、cAdvisor暴露的Prometheus指标三、Node Exporter3.1、安装Node Exporter3.2、指标四、Prometheus4.1、安装4.2、规则配置4.3、报警管理器五、grafana一、前言 cAdvisor源码 node exp…...

<Linux>进程概念
文章目录一、什么是进程1.进程概念2.进程描述 – PCB3.task_struct内容分类二、进程的基本操作1.查看进程2.结束进程3.通过系统调用获取进程标示符4.通过系统调用创建子进程(fork)三、进程状态1.普遍的操作系统状态2.Linux操作系统状态四、两种特殊的进程1.僵尸进程2.孤儿进程五…...
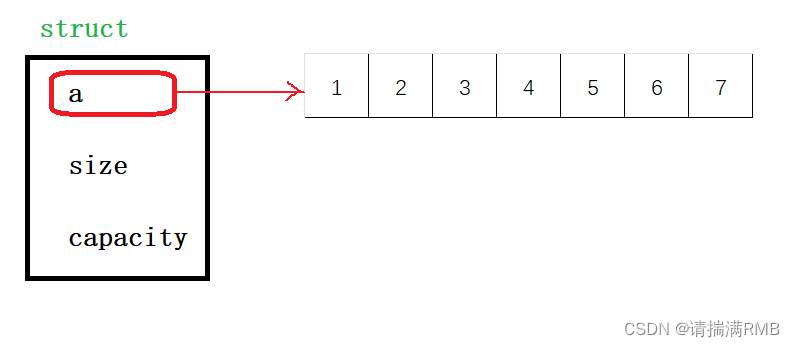
数据结构——顺序表
文章目录🐨0. 前言🎈1. 顺序表的概念及定义🪁2. 接口的声明🪄3. 接口的实现🍅3.1 为何使用断言?🍒3.2 初始化与销毁🍓3.3 尾插与尾删🍉3.4 头插与头删🍹3.5 指…...

闪存系统性能优化方向集锦?AC timing? Cache? 多路并发?
1. 从Flash系统的性能提升说起从消费级产品到数据中心企业级场景,NAND Flash凭借其高性能、大容量、低功耗以及低成本等特性大受欢迎,是目前应用最为广泛的半导体非易失存储介质。为了满足业务场景越来越严苛的性能要求,人们想了许多方法来提…...

【每日一题】——网购
🌏博客主页:PH_modest的博客主页 🚩当前专栏:每日一题 💌其他专栏: 🔴 每日反刍 🟢 读书笔记 🟡 C语言跬步积累 🌈座右铭:广积粮,缓称…...
百度终于要出手了?文心一言
文心一言 百度全新一代知识增强大语言模型,文心大模型家族的新成员,能够与人对话互动,回答问题,协助创作,高效便捷地帮助人们获取信息、知识和灵感。 前几天炒的风风火火的ChatGPT,虽然 ChatGPT 很强大&a…...
8年Java架构师面试官教你正确的面试姿势,10W字面试题带你成功上岸大厂
从最开始的面试者变成现在的面试官,工作多年以及在面试中,我经常能体会到,有些面试者确实是认真努力工作,但坦白说表现出的能力水平却不足以通过面试,通常是两方面原因: 1、“知其然不知其所以然”。做了多…...

Mybatis-Plus详解
简介MyBatis-Plus (opens new window)(简称 MP)是一个 MyBatis (opens new window)的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。特性(官网提供)无侵入:只做增强…...

MongoDB分片集群实战:从零搭建高可用分布式数据库
1. 为什么你需要一个MongoDB分片集群? 如果你正在读这篇文章,我猜你大概率已经遇到了单台MongoDB服务器的瓶颈。可能是磁盘空间快满了,加硬盘也解决不了根本问题;也可能是查询速度越来越慢,即使加了索引,面…...

7步快速参与Git-Stats开源项目开发:新手友好的社区贡献指南
7步快速参与Git-Stats开源项目开发:新手友好的社区贡献指南 【免费下载链接】git-stats 🍀 Local git statistics including GitHub-like contributions calendars. 项目地址: https://gitcode.com/gh_mirrors/gi/git-stats Git-Stats是一个强大的…...

容器镜像签名验证:多方信任与策略管理的终极指南
容器镜像签名验证:多方信任与策略管理的终极指南 【免费下载链接】skopeo Work with remote images registries - retrieving information, images, signing content 项目地址: https://gitcode.com/GitHub_Trending/sk/skopeo 在容器化应用的生命周期中&…...

告别繁琐构建:用Task优雅实现自动化任务管理
告别繁琐构建:用Task优雅实现自动化任务管理 【免费下载链接】task A task runner / simpler Make alternative written in Go 项目地址: https://gitcode.com/gh_mirrors/ta/task Task是一款用Go语言编写的现代化任务运行工具,作为Make的轻量级替…...

IPED敏感信息脱敏工具:自动替换报告中的敏感数据
IPED敏感信息脱敏工具:自动替换报告中的敏感数据 【免费下载链接】IPED IPED Digital Forensic Tool. It is an open source software that can be used to process and analyze digital evidence, often seized at crime scenes by law enforcement or in a corpor…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 