计数,桶与基数排序
目录
一. 计数排序
概念
步骤思路如下
实现代码如下
时间复杂度与空间复杂度
1. 时间复杂度
2. 空间复杂度
计数排序的特点
二. 桶排序
概念
步骤思路如下
实现代码如下
时间复杂度与空间复杂度
1. 时间复杂度
2. 空间复杂度
桶排序的特点
三. 基数排序
概念
步骤思路如下
实现代码如下
时间复杂度与空间复杂度
1. 时间复杂度
2. 空间复杂度
基数排序的特点
一. 计数排序
概念
计数排序是一种非比较排序算法,它的基本思想是利用数组下标的有序性,将元素作为计数数组的相应下标,并在该下标位置存储相应的元素数量,最后根据计数数组填充待排序数组
步骤思路如下
1. 找出待排序数组中的最大值和最小值
遍历待排序数组,找出其中的最大值和最小值。2. 创建计数数组
创建一个新的计数数组,其大小为(最大值 - 最小值 + 1)。
初始化计数数组的所有元素为0。3. 统计元素出现的次数
再次遍历待排序数组,对于数组中的每个元素,将其值减去最小值(为了使得计数数组的下标从0开始),并将计数数组中对应下标的值加1。4. 利用计数数组排序
从后向前遍历待排序数组(从大到小是为了保证稳定性,即相同元素在排序后保持原有顺序)。
对于每个元素,将其值减去最小值,然后利用计数数组找到其在排序后数组中的位置,并将该元素放到正确的位置上。
同时,将计数数组中对应位置的值减1,表示该位置已经被占用。5. 完成排序
实现代码如下
void CountSort(int* a,int n)
{int max=a[0], min=a[0];for (int i = 0; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int* tmp = (int*)calloc(max - min +1, sizeof(int));//自动将值其置为0for (int i = 0; i < n; i++){tmp[a[i] - min]++;}int count = n-1;for (int i = max - min; i >=0; i--){while (tmp[i]--) {a[count--] = i + min;}}free(tmp);tmp = NULL;
}时间复杂度与空间复杂度
1. 时间复杂度
统计元素出现次数的时间复杂度为 O(n)。
根据计数数组进行排序的时间复杂度为 O(n)。
综上所述计数排序的时间复杂度为一般 O(n)。
2. 空间复杂度
由于计数排序需要额外的空间来存储计数数组
所以计数排序的空间复杂度主要取决于计数数组的大小,即 n。因此,计数排序的空间复杂度为 O(n)。
计数排序的特点
计数排序适用于待排序数组中的元素为非负整数(负数不是不能排),并且元素的取值范围不大于计算机可以表示的最大范围。
如果待排序数组中的元素是负数,或者元素的取值范围较大,计数排序可能不适用,因为它需要额外的空间来存储计数数组。
计数排序是一种稳定的排序算法,即相同元素在排序后保持原有的顺序。计数排序的时间复杂度为O(n),其中n是待排序数组的长度
二. 桶排序
概念
桶排序是一种分配式排序算法,它将待排序的数据分到有限数量的桶子里。每个桶子再个别排序(可能使用别的排序算法或以递归方式继续使用桶排序进行排序)。当要被排序的数组内的数值是均匀分布的时候,桶排序使用线性时间(O(n))
步骤思路如下
1.创建n个桶
2. 将待排序元素分散到各个桶中
3. 对每个桶内的元素排序(可以使用别的排序算法)
4. 读取每个桶的元素,按顺序放回原数组中
实现代码如下
#define BUCKET_SIZE 100
#define MAX_NUM 10
void BucketSort(int arr[], int n) {if (n <= 1) {return;}int bucket[BUCKET_SIZE][MAX_NUM / BUCKET_SIZE + 1]; // 桶数组,每个桶的大小为MAX_NUM/BUCKET_SIZE+1int bucketIndex[BUCKET_SIZE] = { 0 }; // 每个桶的当前元素数量// 将元素放入对应的桶中for (int i = 0; i < n; i++) {int index = arr[i] / BUCKET_SIZE; // 计算桶的索引bucket[index][bucketIndex[index]++] = arr[i]; // 将元素放入桶中}// 对每个桶进行排序for (int i = 0; i < BUCKET_SIZE; i++) {if (bucketIndex[i] > 0) {InsertSort(bucket[i], bucketIndex[i]); // 使用插入排序对桶内元素进行排序// 将桶内元素放回原数组for (int j = 0; j < bucketIndex[i]; j++) {arr[i * (MAX_NUM / BUCKET_SIZE + 1) + j] = bucket[i][j];}}}
}时间复杂度与空间复杂度
1. 时间复杂度
①最坏情况
若数据的分布非常不均匀,几乎所有的元素都进入一个桶中,那么桶排序时间复杂度为O(N²)
②最好情况
如果数据分布非常均匀,每个桶中元素数量大致相同,并且使用其他排序算法也达到最佳的时间复杂度,那桶排序时间复杂度为O(N)
③平均情况
平均情况下桶排序时间复杂度大概为O(N)
2. 空间复杂度
空间复杂度大概为O(N+M),其中M为桶的数量,N为开辟数组长度
桶排序的特点
适用于大量数据的排序,是一种高效的排序算法。相比于比较排序算法,桶排序不需要进行元素之间的比较,因此在某些情况下可以更快地完成排序。
是稳定的排序算法,相同元素的相对顺序不会改变。
需要额外的空间来存储桶,如果待排序元素数量较大,可能会占用较多的内存空间。适用于待排序元素分布均匀的情况。对于分布不均匀的数据,可能导致桶的数量不均衡,影响排序效率。
适用场景
例如在对年龄、成绩等具有一定范围的数据进行排序时。当待排序元素数量较大,且数据分布较为均匀时,桶排序可以提供较高的排序效率。
三. 基数排序
概念
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较,直至完成最高位比较
步骤思路如下
1. 寻找待排序数组中最大的数,并确定其是几位数
2. 创建两个数组,一个二维数组,一个一维数组,进入循环,最高位有多少循环多少次(从1开始,因为没有第0位)
3. (使两个数组元素为0)使用一维数组记录当前位的每个数出现的次数
4. 使用前缀和记录下来<=i数字的数量
5. 从后往前遍历存入数据(从大到小是为了保证稳定性,即相同元素在排序后保持原有顺序)。
6. 通过遍历给原数组赋值
7. 重复 2,3,4,5,6 操作直至结束
实现代码如下
int GetDigit(int x,int i)
{int count = x;int n = i;while (--n>0){count /= 10;}count %= 10;return count;
}
void RadixSort(int* a, int n)
{int max=a[0];for (int i = 0; i < n; i++){if (a[i] > max)max = a[i];}int digit1 = 0;while (max){max /= 10;digit1++;}int bucket[10][20];int tmp[20] = { 0 };//桶for(int i = 1;i<=digit1;i++){memset(bucket, 0, sizeof(bucket));memset(tmp, 0, sizeof(tmp));for (int j = 0; j < n; j++){int digit2 = GetDigit(a[j], i);tmp[digit2]++;}for (int j = 1; j < 10; j++)//前缀和记录桶中tmp[i]表示小于等于i的数字数量{tmp[j] += tmp[j - 1];}for (int j = n - 1; j >= 0; j--){int digit2 = GetDigit(a[j],i);bucket[digit2][tmp[digit2]--] = a[j];}int k = 0;for (int d = 0; d < 10; d++){for (int j = 0; j < 20; j++){if(bucket[d][j]!=0)a[k++] = bucket[d][j];}}}
}时间复杂度与空间复杂度
1. 时间复杂度
要进行 i(最高位的位数) 趟排序 , 每趟排序需要将元素分派到k个桶,所以每趟排序的时间复杂度为O(n+k) 走i趟时间复杂度就为O(i(n+k)) 但桶的个数通常是固定的,执行的躺数一般又较小,所以基数排序的时间复杂度趋近于O(n)
2. 空间复杂度
由于开辟了两个数组辅助,假设两个数组长度分别为N,M,所以基数排序的空间复杂度大概为O(N+M)
基数排序的特点
基数排序是一种稳定的排序算法。在排序过程中,相同元素的相对顺序保持不变。这是因为基数排序是按照数字的每一位进行排序的,而相同元素的每一位都是相同的,所以它们的相对顺序不会发生变化。
基数排序是一种非比较型排序算法,它不通过比较元素的大小来进行排序,而是通过分配和收集的方式实现排序。这使得基数排序在某些情况下比基于比较的排序算法(如快速排序、归并排序等)更加高效。
基数排序特别适用于对整数进行排序,尤其是当待排序的整数范围不大,且整数位数相差不大时。在这种情况下,基数排序的效率很高,因为只需要进行有限次的分配和收集操作。
基数排序需要额外的空间来存储桶(或子数组),以便进行元素的分配和收集。如果待排序的元素数量很大,这可能会占用较多的内存空间。因此,在使用基数排序时,需要考虑内存使用情况。
基数排序的时间复杂度可以近似认为是线性的。这使得基数排序在处理大数据集时具有较高的效率。
基数排序不仅适用于数组排序,还适用于链表排序。因为链表在分配和收集元素时不需要移动元素本身,只需要改变节点的指针指向即可。这使得基数排序在链表排序中具有更高的效率。
这篇就到这里啦,感谢支持
(๑′ᴗ‵๑)I Lᵒᵛᵉᵧₒᵤ❤
相关文章:

计数,桶与基数排序
目录 一. 计数排序 概念 步骤思路如下 实现代码如下 时间复杂度与空间复杂度 1. 时间复杂度 2. 空间复杂度 计数排序的特点 二. 桶排序 概念 步骤思路如下 实现代码如下 时间复杂度与空间复杂度 1. 时间复杂度 2. 空间复杂度 桶排序的特点 三. 基数排序 概念 步…...

unity渲染人物模型透明度问题
问题1:有独立的手和衣服的模型,但最终只渲染出来半透明衣服 问题2:透明度贴图是正确的但显示却不正确 这上面两个模型的问题都是因为人物模型是一个完整的,为啥有些地方可以正常显示,有些地方透明度却有问题。 其中…...

CH03_布局
第3章:布局 本章目标 理解布局的原则理解布局的过程理解布局的容器掌握各类布局容器的运用 理解 WPF 中的布局 WPF 布局原则 WPF 窗口只能包含单个元素。为在WPF 窗口中放置多个元素并创建更贴近实用的用户男面,需要在窗口上放置一个容器&#x…...

【Oracle】Oracle中的merge into
目录 解释使用场景语法示例案例一案例二 MERGE INTO的优缺点优点:缺点: 注意事项附:Oracle中的MERGE INTO实现的效果,如果改为用MySQL应该怎么实现注意 解释 在Oracle数据库中,MERGE INTO是一种用于对表进行合并&…...
【论文阅读笔记】In Search of an Understandable Consensus Algorithm (Extended Version)
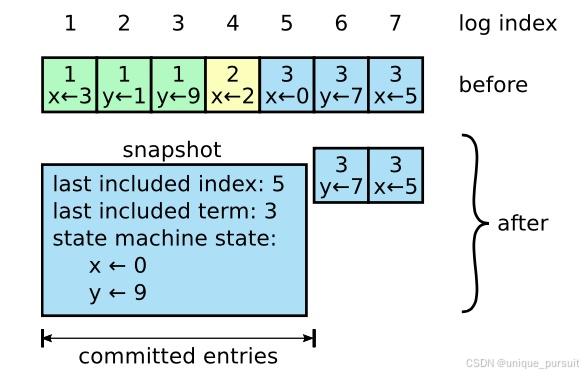
1 介绍 分布式一致性共识算法指的是在分布式系统中,使得所有节点对同一份数据的认知能够达成共识的算法。且算法允许所有节点像一个整体一样工作,即使其中一些节点出现故障也能够继续工作。之前的大部分一致性算法实现都是基于Paxos,但Paxos…...
CentOS 7 网络配置
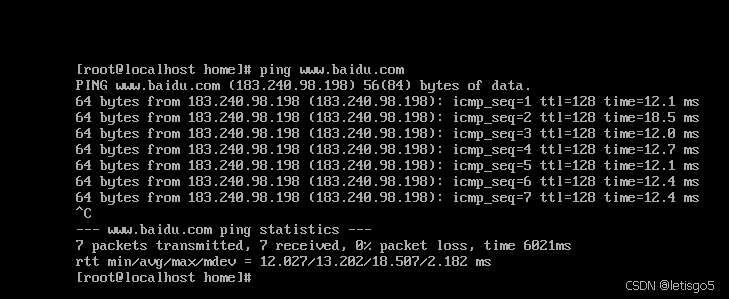
如想了解请查看 虚拟机安装CentOS7 第一步:查看虚拟机网络编辑器、查看NAT设置 (子网ID,网关IP) 第二步:配置VMnet8 IP与DNS 注意事项:子网掩码与默认网关与 第一步 保持一致 第三步:网络配置…...
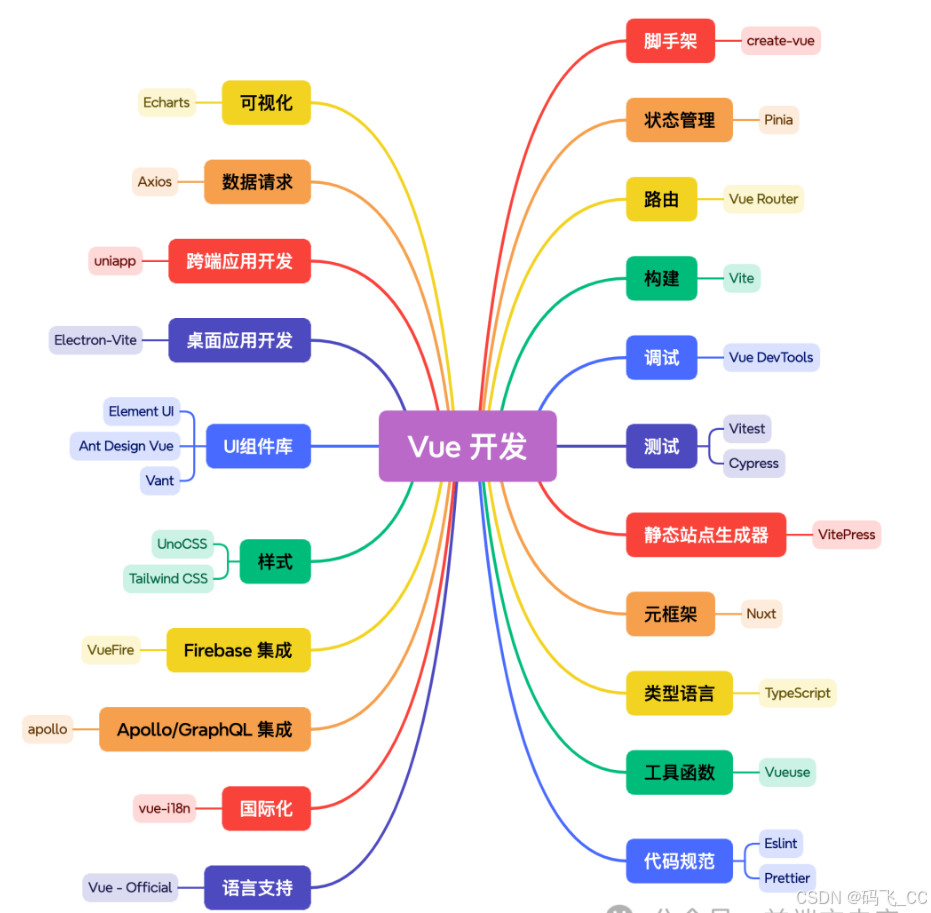
2024 React 和 Vue 的生态工具
react Vue...

AI学习指南机器学习篇-t-SNE模型应用与Python实践
AI学习指南机器学习篇-t-SNE模型应用与Python实践 在机器学习领域,数据的可视化是非常重要的,因为它可以帮助我们更好地理解数据的结构和特征。而t-SNE(t-distributed Stochastic Neighbor Embedding)是一种非常强大的降维和可视…...

小试牛刀-Telebot区块链游戏机器人
目录 1.编写目的 2.实现功能 2.1 Wallet功能 2.2 游戏功能 2.3 提出功能 2.4 辅助功能 3.功能实现详解 3.1 wallet功能 3.2 游戏功能 3.3 提出功能 3.4 辅助功能 4.测试视频 Welcome to Code Blocks blog 本篇文章主要介绍了 [Telebot区块链游戏机器人] ❤博主…...
使用github actions构建多平台electron应用
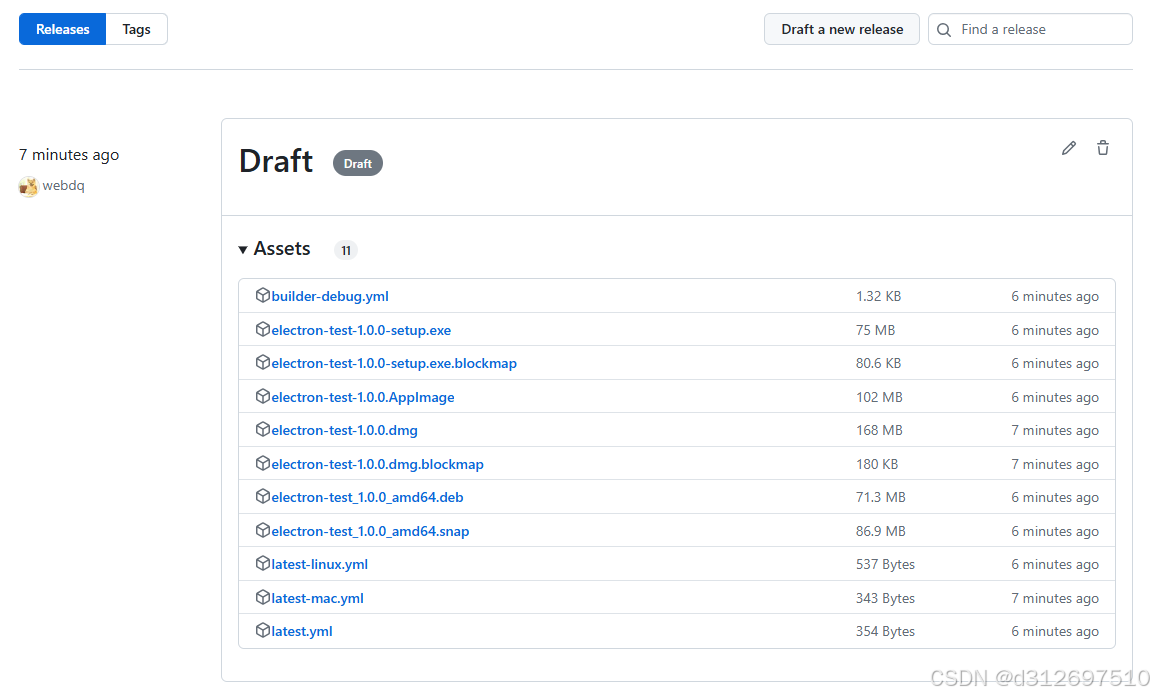
1. 创建electron项目 使用pnpm创建项目 pnpm create quick-start/electron 2. 修改electron-builder.yml文件 修改mac的target mac:target:- target: dmgarch: universal 3. 添加workflow 创建 .github/workflows/main.yml 文件 name: Build/release Electron appon:work…...

java通过pdf-box插件完成对pdf文件中图片/文字的替换
需要引入的Maven依赖: <!-- pdf替换图片 --><dependency><groupId>e-iceblue</groupId><artifactId>spire.pdf.free</artifactId><version>5.1.0</version></dependency> java代码: public AjaxResult replacepd…...

鸿蒙 next 5.0 版本页面跳转传参 接受参数 ,,接受的时候 要先定义接受参数的类型, 代码可以直接CV使用 [教程]
1, 先看效果 2, 先准备好两个页面 index 页面 传递参数 import router from ohos.routerEntry Component struct Index {Statelist: string[] [星期一, 星期二,星期三, 星期四,星期五]StateactiveIndex: number 0build() {Row() {Column({ space: 10 }) {ForEach(this.list,…...

【electron6】浏览器实时播放PCM数据
pcm介绍:PCM(Puls Code Modulation)全称脉码调制录音,PCM录音就是将声音的模拟信号表示成0,1标识的数字信号,未经任何编码和压缩处理,所以可以认为PCM是未经压缩的音频原始格式。PCM格式文件中不包含头部信…...
嵌入式C/C++、FreeRTOS、STM32F407VGT6和TCP:智能家居安防系统的全流程介绍(代码示例)
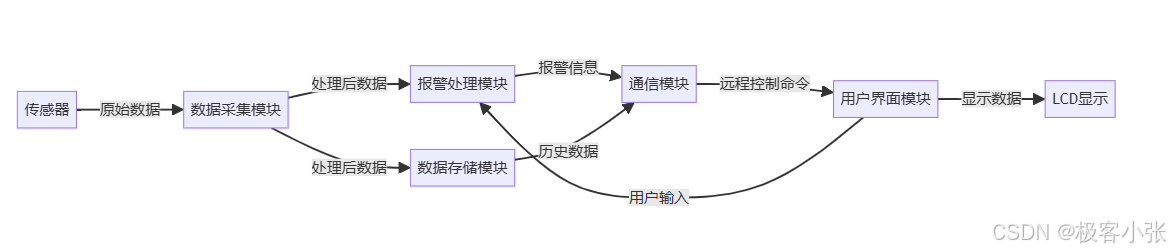
1. 项目概述 随着物联网技术的快速发展,智能家居安防系统越来越受到人们的重视。本文介绍了一种基于STM32单片机的嵌入式安防中控系统的设计与实现方案。该系统集成了多种传感器,实现了实时监控、报警和远程控制等功能,为用户提供了一个安全、可靠的家居安防解决方案。 1.1 系…...
【Django】django自带后台管理系统样式错乱,uwsgi启动css格式消失的问题
正常情况: ERROR:(css、js文件加载失败) 问题:CSS加载的样式没有了,原因:使用了django自带的admin,在使用 python manage.py runserver启动 的时候,可以加载到admin的文…...

解决npm install(‘proxy‘ config is set properly. See: ‘npm help config‘)失败问题
摘要 重装电脑系统后,使用npm install初始化项目依赖失败了,错误提示:‘proxy’ config is set properly…,具体的错误提示如下图所示: 解决方案 经过报错信息查询解决办法,最终找到了两个比较好的方案&a…...

汽车及零部件研发项目管理系统:一汽东机工选择奥博思 PowerProject 提升研发项目管理效率
在汽车行业中,汽车零部件的研发和生产是一个关键的环节。随着汽车市场的不断扩大和消费者需求的不断增加,汽车零部件项目管理的重要性日益凸显。通过有效的项目管理方法及利用先进的数字项目管理系统,可以大幅提高项目的成功率和顺利度&#…...
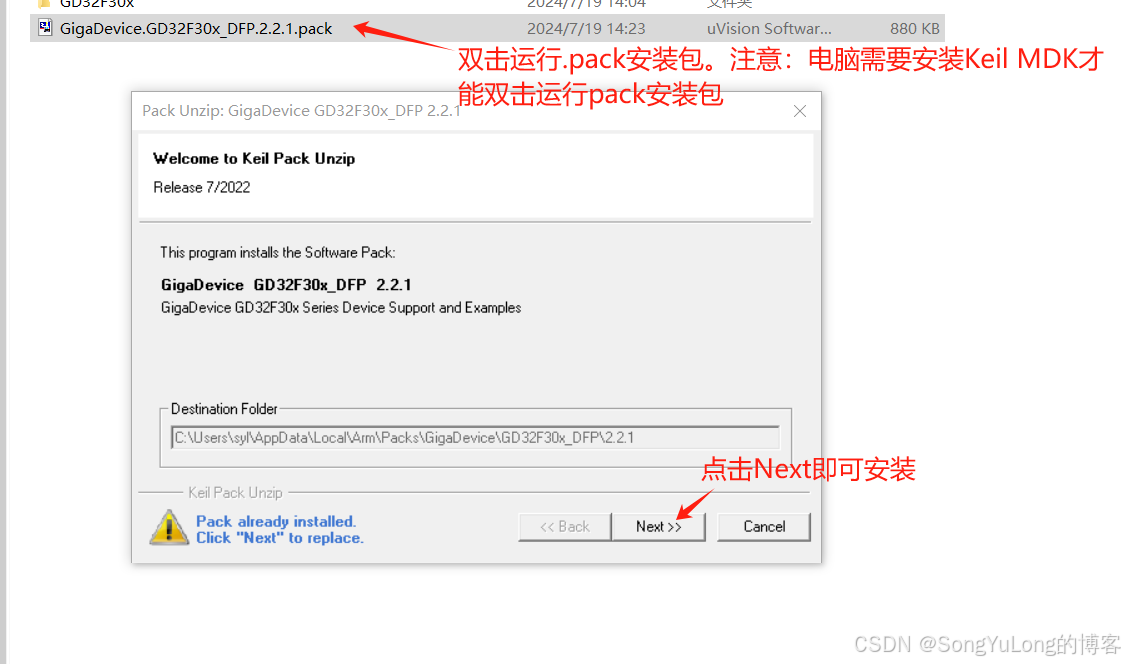
Keil开发IDE
Keil开发IDE 简述Keil C51Keil ARMMDK DFP安装 简述 Keil公司是一家业界领先的微控制器(MCU)软件开发工具的独立供应商。Keil公司由两家私人公司联合运营,分别是德国慕尼黑的Keil Elektronik GmbH和美国德克萨斯的Keil Software Inc。Keil公…...
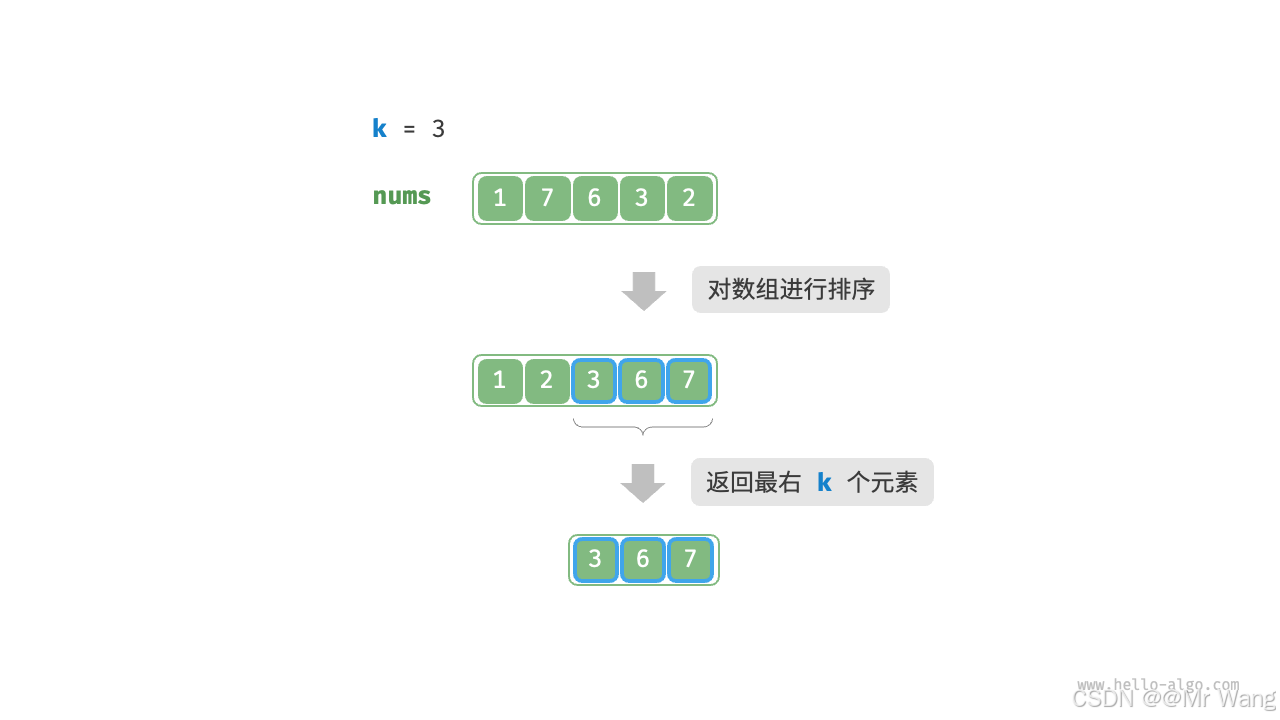
数据结构与算法05堆|建堆|Top-k问题
一、堆 1、堆的介绍 堆(heap)是一种满足特定的条件的完全二叉树,主要可以分为大根堆和小根堆。 大根堆(max heap):任意节点的值大于等于其子节点的值。小根堆(min heap)࿱…...

【精简版】jQuery 中的 Ajax 详解
目录 一、概念 二、jQuery 发送 GET 请求 三、jQuery 发送 POST 请求 四、$.ajax() 方法 1、含义 2、settings 选项 ① type 属性 ② async 属性 ③ headers 属性 ④ contentType 属性 ⑤ processData 属性 ⑥ data 属性 ⑦ timeout 属性 ⑧ beforeSend(jqXHR) 方…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
