graham 算法计算平面投影点集的凸包
文章目录
- 向量的内积(点乘)、外积(叉乘)
- 确定旋转方向
- numpy 的 cross 和 outer
- `np.inner` 向量与矩阵计算示例
- `np.outer` 向量与矩阵计算示例
- python 示例
- 生成样例散点数据图
- 显示按极角排序的结果
- 根据排序点计算向量转向并连成凸包
- 基本思路
将三维空间中的点云使用 BEV 的方式多视角投影到某个平面之后,可能需要用到该平面投影图(光栅化之前)的点集的凸包,所以这里记录一下常见的 graham 凸包算法。
向量的内积(点乘)、外积(叉乘)
graham 算法模拟最外层点集包围的过程的关键思想是使用两个向量之间的外积来判断下一条连线的转角,如果向外拐了,那说明当前基点在本次连线之后会成为一块凹陷,注意“凸包”的定义,每个顶角的角度都小于 18 0 ∘ 180^\circ 180∘ 才叫 “凸” ,如果有一个内凹顶点,那么它的内角是大于 18 0 ∘ 180^\circ 180∘ 的,可以确定,它应该是包含在实际的最终计算出来的理想凸包之内才对,这个时候就需要调整连线的基点为上一个基点。
在二维平面上,叉积的结果与向量的顺时针或逆时针旋转方向有关。具体来说:
- 对于二维平面上的两个向量 u = ( x 1 , y 1 ) u=(x_1,y_1) u=(x1,y1) 和 v = ( x 2 , y 2 ) v=(x_2, y_2) v=(x2,y2) ,它们的叉积可以使用一个标量值来表示 u × v = x 1 y 2 − y 1 x 2 u\times v = x_1y_2 - y_1x_2 u×v=x1y2−y1x2
- 这个标量值表示了这两个向量所定义的平行四边形的有向面积,也可以用来判定向量的旋转方向。
确定旋转方向
- 正值:当 叉积 的值为正时,向量 v v v 从向量 u u u 逆时针旋转到达 v v v,也就是说, v v v 在 u u u 的左侧。
- 负值:当 叉积 的值为负时,向量 v v v 从向量 u u u 顺时针旋转到达 v v v,也就是说, v v v 在 u u u 的右侧。
- 零值:当 叉积 的值为零时,两个向量是共线的,即它们之间没有旋转,或者说它们之间的旋转角度是 0 ∘ 0^\circ 0∘∘ 或 18 0 ∘ 180^\circ 180∘。
numpy 的 cross 和 outer
示例 python 代码:
a = np.array([1, 1])
b = np.array([0, 1])np.cross(a, b)
输出结果为 1 ,代表由向量 a 转动到向量 b 的转角是逆时针,符合右手螺旋。
numpy 库中有两个函数分别是 np.cross(a,b) 和 np.outer(a,b) ,其中 np.cross 是我们常用所说的外积(叉乘),而 np.outer 实际的计算结果定义是一个张量中的每个元素对另一个张量中的每个元素的乘积。
np.inner 向量与矩阵计算示例
# Python Program illustrating
# numpy.inner() method
import numpy as np # Vectors
a = np.array([2, 6])
b = np.array([3, 10])
print("Vectors :")
print("a = ", a)
print("\nb = ", b) # Inner Product of Vectors
print("\nInner product of vectors a and b =")
print(np.inner(a, b)) print("---------------------------------------") # Matrices
x = np.array([[2, 3, 4], [3, 2, 9]])
y = np.array([[1, 5, 0], [5, 10, 3]])
print("\nMatrices :")
print("x =", x)
print("\ny =", y) # Inner product of matrices
print("\nInner product of matrices x and y =")
print(np.inner(x, y))
输出:
Vectors :
a = [2 6]
b = [3 10]Inner product of vectors a and b =
66
---------------------------------------Matrices :
x = [[2 3 4][3 2 9]]y = [[ 1 5 0][ 5 10 3]]Inner product of matrices x and y =
[[17 52][13 62]]
可以看到对于向量来说,外积在 numpy 中的 outer 不是我们说常说的叉乘计算方式,而是一个向量中的每个元素对另一个向量中的每个元素的乘积结果。
np.outer 向量与矩阵计算示例
# Python Program illustrating
# numpy.outer() method
import numpy as np # Vectors
a = np.array([2, 6])
b = np.array([3, 10])
print("Vectors :")
print("a = ", a)
print("\nb = ", b) # Outer product of vectors
print("\nOuter product of vectors a and b =")
print(np.outer(a, b)) print("------------------------------------") # Matrices
x = np.array([[3, 6, 4], [9, 4, 6]])
y = np.array([[1, 15, 7], [3, 10, 8]])
print("\nMatrices :")
print("x =", x)
print("\ny =", y) # Outer product of matrices
print("\nOuter product of matrices x and y =")
print(np.outer(x, y))
输出:
Vectors :
a = [2 6]
b = [3 10]Outer product of vectors a and b =
[[ 6 20][18 60]]
------------------------------------Matrices :
x = [[3 6 4][9 4 6]]y = [[ 1 15 7][ 3 10 8]]Outer product of matrices x and y =
[[ 3 45 21 9 30 24][ 6 90 42 18 60 48][ 4 60 28 12 40 32][ 9 135 63 27 90 72][ 4 60 28 12 40 32][ 6 90 42 18 60 48]]
这说明在 graham 凸包算法中计算两个向量的旋转方向还是需要 np.cross 而不能使用 np.outer 来计算。
python 示例
生成样例散点数据图
# Test the algorithm with an example set of points
points = [(0, 3), (1, 1), (2, 2), (4, 4), (0, 0), (1, 2), (3, 1), (3, 3)]start = min(points, key=lambda p: (p[1], p[0]))print(*zip(*points))fig1 = plt.figure()
plt.scatter(*zip(*points), color='blue')
plt.scatter(*start, color="red")
plt.show()

graham 算法一般以最下最左(Lowest Then Leftest)的点作为基准点,图中以红色的点作为标识。
显示按极角排序的结果
sorted_points = sorted(points, key=lambda p: (p[1] - start[1]) / (p[0] - start[0] + 1e-9), reverse=False)fig, axs = plt.subplots(2, 4)
for point, ax in zip(sorted_points, axs.flatten()):ax.scatter(*zip(*points), color="blue")ax.scatter(*start, color="red")ax.plot(*zip(*[start, point]), marker="o")
plt.show()

根据排序点计算向量转向并连成凸包
def cross_product(o, a, b)return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])hull = []
for p in sorted_points:while len(hull) >= 2 and cross_product(hull[-2], hull[-1], p) <= 0:hull.pop()hull.append(p)fig = plt.figure()
plt.scatter(*zip(*points), color="blue")
for i in range(len(hull)):p1 = hull[i]p2 = hull[(i + 1) % len(hull)]plt.plot([p1[0], p2[0]], [p1[1], p2[1]], 'r-')
plt.show()

基本思路
- 选取基点(最左最下)
- 所有点与基点形成的向量进行极角排序,从小到大
- 从当前点(初始时是基点 p 0 p_0 p0 ) p i p_i pi 出发连接极角排序好的点序列中的下一个点 p i + 1 p_{i+1} pi+1
- 从第一个点 p 1 p_1 p1 连接第二个点 p 2 p_2 p2 ,判断前一个向量 p 0 p 1 → \overrightarrow{p_0p_1} p0p1 与新的向量 p 1 p 2 → \overrightarrow{p_1p_2} p1p2 的转向是否是往内拐,如果是外拐的话说明这个地方会形成一个凹陷,不是凸包连线,所以弹出这个新加入的点 p 2 p_2 p2 ,准备下一个点的测试
相关文章:

graham 算法计算平面投影点集的凸包
文章目录 向量的内积(点乘)、外积(叉乘)确定旋转方向numpy 的 cross 和 outernp.inner 向量与矩阵计算示例np.outer 向量与矩阵计算示例 python 示例生成样例散点数据图显示按极角排序的结果根据排序点计算向量转向并连成凸包 基本…...

【海外云手机】静态住宅IP集成解决方案
航海大背景下,企业和个人用户对于网络隐私、稳定性以及跨国业务的需求日益增加。静态住宅IP与海外云手机的结合,提供了一种创新的集成解决方案,能够有效应对这些需求。 本篇文章分为三个部分;静态住宅优势、云手机优势、集成解决…...
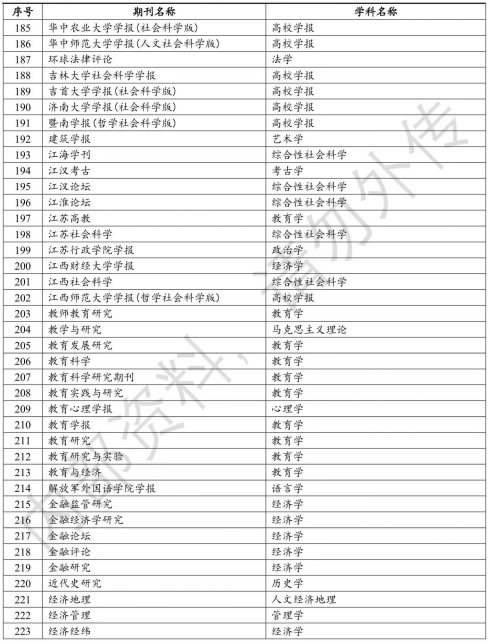
最新!CSSCI(2023-2024)期刊目录公布!
【SciencePub学术】据鲁迅美术学院7月16日消息,近日,南京大学中国社会科学研究评价中心公布了中文社会科学引文索引(CSSCI)(2023—2024)数据库最新入选目录。 C刊一般指CSSCI来源期刊,即南大核心…...

C语言 | Leetcode C语言题解之第237题删除链表中的节点
题目: 题解: /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/void deleteNode(struct ListNode* node) {struct ListNode * p node->next;int temp;temp node->val;node->val…...

linux LED代码设计
设计目标: 写RGB LED灭、亮、闪烁等效果,不同颜色也需要设置 #include <iostream> #include <unistd.h> // 对于usleep() #include <fcntl.h> // 对于open(), close() #include <sys/ioctl.h> // 对于ioctl() #include <li…...

Jvm基础(一)
目录 JVM是什么运行时数据区域线程私有1.程序计数器2.虚拟机栈3.本地方法栈 线程共享1.方法区2.堆 二、对象创建1.给对象分配空间(1)指针碰撞(2)空闲列表 2.对象的内存布局对象的组成Mark Word类型指针实例数据:对齐填充 对象的访问定位句柄法 三、垃圾收集器和内存…...

深入理解FFmpeg--软/硬件解码流程
FFmpeg是一款强大的多媒体处理工具,支持软件和硬件解码。软件解码利用CPU执行解码过程,适用于各种平台,但可能对性能要求较高。硬件解码则利用GPU或其他专用硬件加速解码,能显著降低CPU负载,提升解码效率和能效。FFmpe…...

新的铸造厂通过 PROFIBUS 技术实现完全自动化
钢铁生产商某钢以其在厚钢板类别中极高的产品质量而闻名。其原材料(板坯连铸机)在钢铁厂本地生产,该厂最近新建了一座垂直连铸厂。该项目的一个主要目标是从一开始就完全自动化这座新工厂和整个铸造过程,以高成本效率实现最佳产品…...
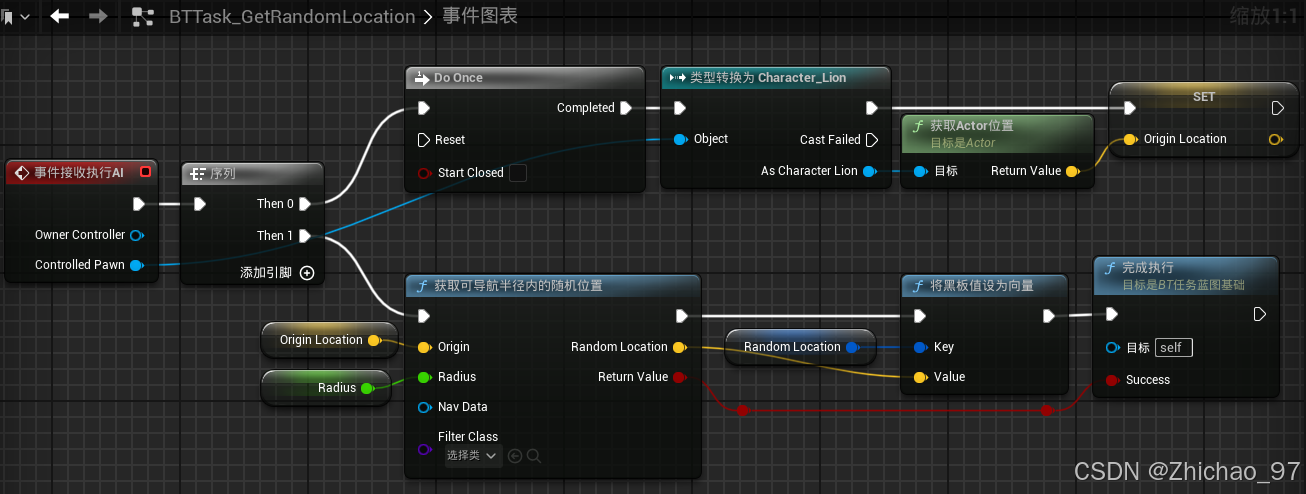
【UE5.1】NPC人工智能——04 NPC巡逻
效果 步骤 一、准备行为树和黑板 1. 对我们之前创建的AI控制器创建一个子蓝图类 这里命名为“BP_NPC_AIController_Lion”,表示专门用于控制狮子的AI控制器 2. 打开狮子蓝图“Character_Lion” 在类默认值中将“AI控制器类”修改为“BP_NPC_AIController_Lion” 3…...

计算机视觉主流框架及其应用方向
文章目录 前言一、计算机视觉领域的主要框架1、深度学习框架1.1、TensorFlow1.2、PyTorch 2、神经网络模型2.1、卷积神经网络(CNN)2.2、循环神经网络(RNN) 二、框架在计算机视觉任务中的应用1、TensorFlow1.1、概述:1.…...

群晖 搭建alist 记录
docker搭建 使用docker-compose 创建一个 docker-compose.yml version: 3.5services:qbittorrent:image: linuxserver/qbittorrent:latestcontainer_name: qbittorrent# network_mode: hostenvironment:- PUID1000- PGID100- TZAsia/Shanghai- WEBUI_PORT8181 # 将外部端口…...

【北航主办丨本届SPIE独立出版丨已确认ISSN号】第三届智能机械与人机交互技术学术会议(IHCIT 2024,7月27)
由北京航空航天大学指导,北京航空航天大学自动化科学与电气工程学院主办,AEIC学术交流中心承办的第三届智能机械与人机交互技术学术会议(IHCIT 2024)将定于2024年7月27日于中国杭州召开。 大会面向基础与前沿、学科与产业…...

深入浅出WebRTC—NACK
WebRTC 中的 NACK(Negative Acknowledgment)机制是实时通信中处理网络丢包的关键组件。网络丢包是常见的现象,尤其是在无线网络或不稳定连接中。NACK 机制旨在通过请求重传丢失的数据包来减少这种影响,从而保持通信的连续性和质量…...

简单工厂模式、工厂模式和抽象工厂模式的区别
简单工厂模式、工厂模式和抽象工厂模式都是创建型设计模式,它们之间在目的、实现方式和适用场景上存在显著的区别。以下是对这三种模式的详细比较: 一、定义与目的 简单工厂模式(Simple Factory Pattern) 定义: 简单工…...
JVM-垃圾回收与内存分配
目录 垃圾收集器与内存分配策略 引用 对象的访问方式有哪些?(句柄和直接指针) Java的引用有哪些类型? 如何判断对象是否是垃圾? 请列举一些可作为GC Roots的对象? 对象头了解吗? mark word(hashcode、分代、锁标志位)、…...

Jolt路线图
1. 引言 a16z crypto团队2024年7月更新了其Jolt路线图: 主要分为3大维度: 1)链上验证维度: 1.1)Zeromorph:见Aztec Labs团队2023年论文 Zeromorph: Zero-Knowledge Multilinear-Evaluation Proofs from…...

NEEP-EN2-2019-Text4
英二-2019-Text4摘自赫芬顿邮报《The Huffington Post》2018年6月的一篇名为“Let’s Stop Pretending Quitting Straws Will Solve Plastic Pollution”的文章。 以下为个人解析,非官方公开标准资料,可能有误,仅供参考。(单词解释…...

docker 部署wechatbot-webhook 并获取接口实现微信群图片自动保存到chevereto图库等
功能如图: docker部署 version: "3" services:excalidraw:image: dannicool/docker-wechatbot-webhook:latestcontainer_name: wechatbot-webhookdeploy:resources:limits:cpus: 0.15memory: 500Mreservations:cpus: 0.05memory: 80Mrestart: alwayspor…...

OpenWrt安装快速入门指南
在刷新 OpenWrt 固件之前,建议进行以下准备: 1、不要急于安装,慢慢来。如果在安装过程中出现奇怪之处,请先找到答案,然后再继续。 2、准备好设备的精确型号,以便能够选择正确的OpenWrt固件。 3、手上有关…...

AIGC Kolors可图IP-Adapter-Plus风格参考模型使用案例
参考: https://huggingface.co/Kwai-Kolors/Kolors-IP-Adapter-Plus 代码环境安装: git clone https://github.com/Kwai-Kolors/Kolors cd Kolors conda create --name kolors python=3.8 conda activate kolors pip install -r requirements.txt python3 setup.py install…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
