【算法】跳跃游戏II
难度:中等
题目:
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
解题思路
这道题目的解决方案可以通过贪心算法来实现,核心思想是尽可能地让每次跳跃都能让我们到达更远的位置。
-
理解问题
给定一个非负整数数组nums,数组中的每个元素表示你从当前位置可以跳跃的最大长度,目标是到达数组的最后一个位置。要求找到到达最后一个位置所需的最小跳跃次数。 -
初始设置
● 初始化jumps为0,表示跳跃次数。
● 初始化maxReach为0,用来记录当前能到达的最远位置。
● 初始化lastJumpPos为0,记录上一次跳跃后能到达的最远位置。 -
遍历数组
遍历数组nums,直到倒数第二个位置(因为到达最后一个位置时自然完成任务,无需额外跳跃)。
在每次迭代中执行以下步骤:
4. 更新最大可达位置:计算当前位置i加上其对应的跳跃能力nums[i],取当前最大可达距离与这个值的最大者,更新maxReach。这样可以确保maxReach始终记录着以当前位置为起点能跳到的最远位置。
5. 判断是否需要跳跃:如果当前遍历到了上一次跳跃所能达到的最远位置(即i === lastJumpPos),说明需要进行下一次跳跃。此时,jumps加1,并将lastJumpPos更新为当前的maxReach。这表示从当前位置开始,至少需要一次跳跃来覆盖剩余的距离。
- 结果返回
遍历结束后,jumps即为到达数组最后一个位置所需的最小跳跃次数。
为什么这种方法有效?
这种方法充分利用了贪心策略,每一步都试图做出最优选择,即尽可能通过较少的跳跃覆盖更远的距离。通过维护一个不断向前推进的“最远可达边界”,我们确保了在每次跳跃时都选择了最经济的方案,从而减少了总的跳跃次数。
通过这种方式,我们避免了暴力搜索或复杂的动态规划状态转移,仅通过一次遍历就高效解决了问题。
JavaScript代码实现
function jump(nums) {let n = nums.length;if (n === 1) return 0; // 如果数组只有一个元素,不需要跳跃// jumps表示跳跃次数,maxReach表示当前能到达的最远位置,lastJumpPos表示记录上一次跳跃后能到达的最远位置let jumps = 0, maxReach = 0, lastJumpPos = 0;for (let i = 0; i < n - 1; i++) {// 找到当前能跳到的最远位置maxReach = Math.max(maxReach, i + nums[i]);// 当前位置已经是上次跳跃能达到的最远位置,需要再进行一次跳跃if (i === lastJumpPos) {jumps++;lastJumpPos = maxReach; // 更新下次跳跃需要开始的位置}}return jumps;
}
这段代码实现了题目要求的功能,注意其中对特殊情况的处理,以及如何通过贪心策略逐步推进跳跃的边界,最终计算出最小的跳跃次数。
相关文章:

【算法】跳跃游戏II
难度:中等 题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[…...
学习大数据DAY20 Linux环境配置与Linux基本指令
目录 Linux 介绍 Linux 发行版 Linux 和 Windows 比较 Linux 就业方向: 下载 CentOS Linux 目录树 Linux 目录结构 作业 1 常用命令分类 文件目录类 作业 2 vim 编辑文件 作业 3 你问我第 19 天去哪了?第 19 天在汇报第一阶段的知识总结,没什…...

达梦+flowable改造
原项目springbootflowablemysql模式现需改造springbootflowable达梦, 1.在项目中引入达梦jpa包 引入高版本包已兼容flowable(6.4.2)liquibase(3.6.2) 我没有像网上做覆盖及达梦配置 <dependency> …...

【乐吾乐2D可视化组态编辑器】消息
消息 乐吾乐2D可视化组态编辑器demo:https://2d.le5le.com/ 监听消息 const fn (event, data) > {}; meta2d.on(event, fn);// 监听全部消息 meta2d.on(*, fn);// 取消监听 meta2d.off(event, fn); meta2d.off(*, fn); Copy 系统消息 event(…...
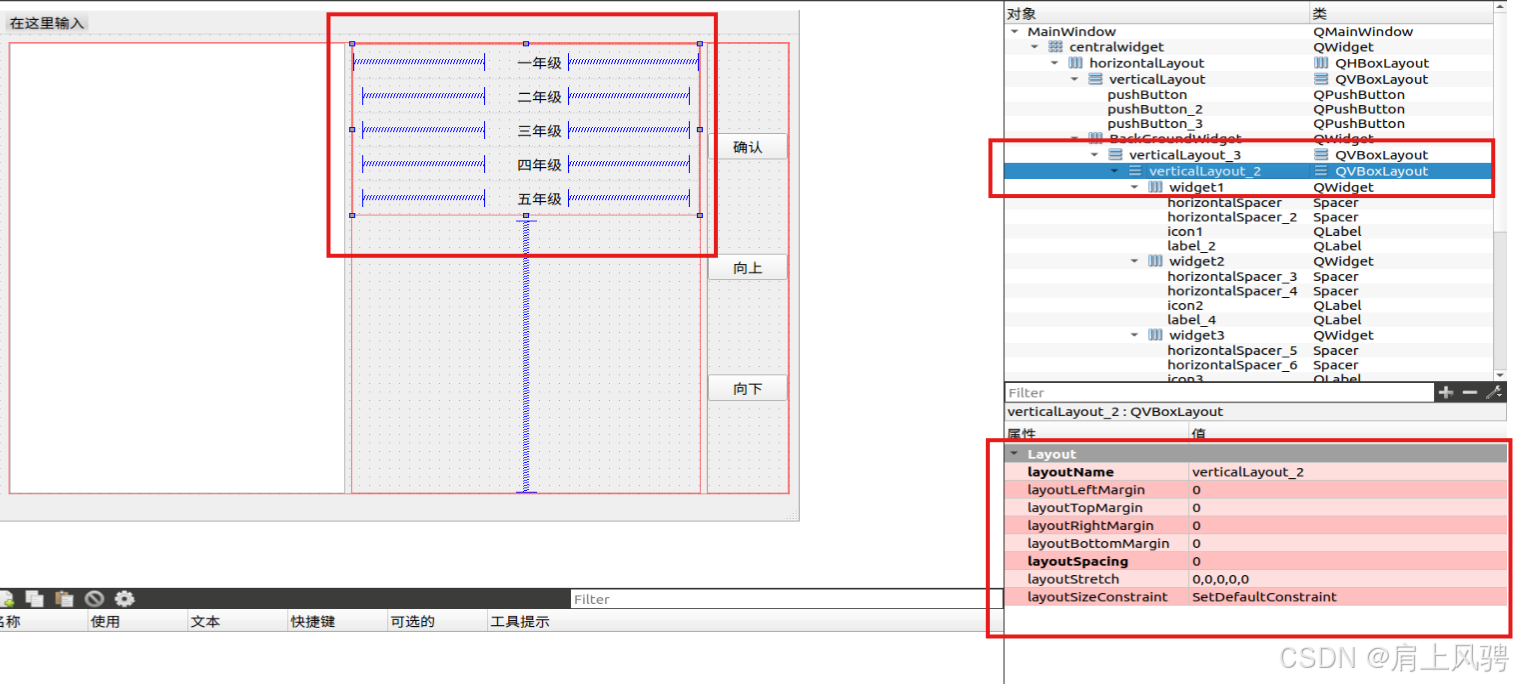
Qt创建列表,通过外部按钮控制列表的选中下移、上移以及左侧图标的显现
引言 项目中需要使用列表QListWidget,但是不能直接拿来使用。需要创建一个列表,通过向上和向下的按钮来向上或者向下移动选中列表项,当当前项背选中再去点击确认按钮,会在列表项的前面出现一个图标。 实现效果 本实例实现的效果如下: 实现思路 思路一 直接采用QLis…...

svn不能记住密码,反复弹出GNOME,自动重置svn.simple文件
1. 修改文件 打开 ~/.subversion/auth/svn.simple/xxx 更新前 K 15 svn:realmstring V 32 xxxxx //svn 地址,库的地址 K 8 username V 4 xxx //用户名 END在顶部插入下面内容, 注意,如果密码不对,则文件文法正常生效 更新后…...
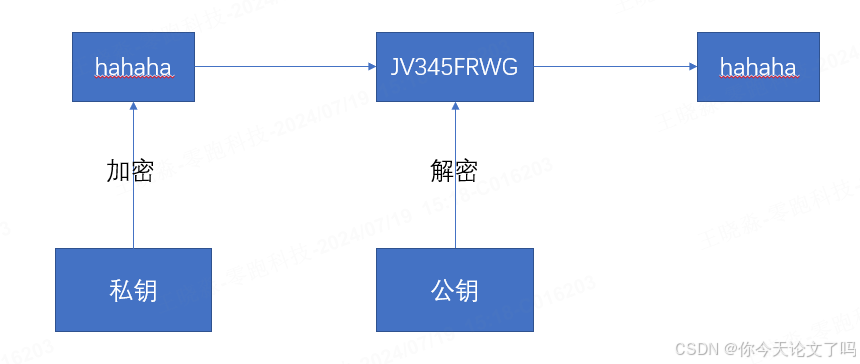
对称加密与非对称加密
对称加密 对称加密指的是加密和解密使用同一个秘钥,所以叫对称加密。对称加密只有一个秘钥,称为私钥。 优点:算法公开、计算量小、加密速度快、效率高 缺点:数据传输前,发送方和接收方必须确定好秘钥,双方也必须要保存好秘钥。 常见对称加密算法: DES、3DES、AES、3…...

03 Git的基本使用
第3章:Git的基本使用 一、创建版本仓库 一)TortoiseGit 选择项目地址,右键,创建版本库 初始化git init版本库 查看是否生成.git文件(隐藏文件) 二)Git 选择项目地址,…...
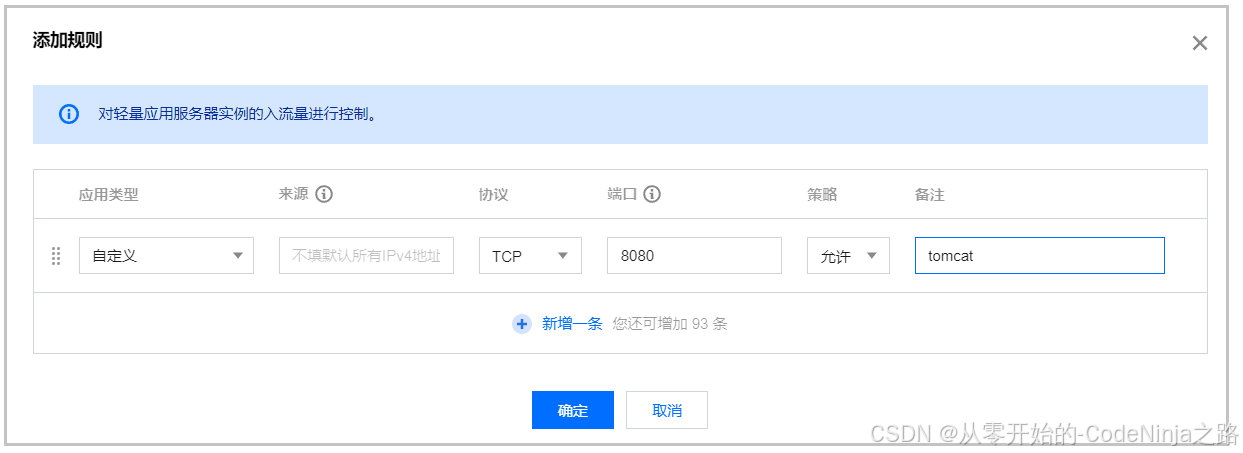
【Linux】将IDEA项目部署到云服务器上,让其成为后台进程(保姆级教学,满满的干货~~)
目录 部署项目到云服务器什么是部署一、 创建MySQL数据库二、 修改idea配置项三、 数据打包四、 部署云服务器五、开放端口号六 、 验证程序 部署项目到云服务器 什么是部署 ⼯作中涉及到的"环境" 开发环境:开发⼈员写代码⽤的机器.测试环境:测试⼈员测试程序使⽤…...
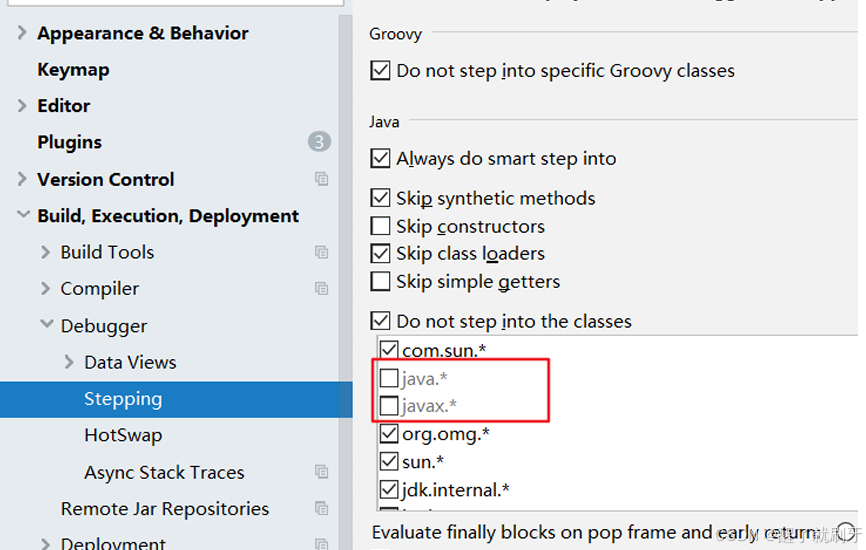
IDEA的断点调试(Debug)
《IDEA破解、配置、使用技巧与实战教程》系列文章目录 第一章 IDEA破解与HelloWorld的实战编写 第二章 IDEA的详细设置 第三章 IDEA的工程与模块管理 第四章 IDEA的常见代码模板的使用 第五章 IDEA中常用的快捷键 第六章 IDEA的断点调试(Debug) 第七章 …...

部署django
部署Django项目到Apache HTTP服务器上,通常会使用mod_wsgi模块,这是Apache的一个扩展,专为Python web应用设计,可以很好地与Django集成。以下是部署Django项目的简要步骤: 准备工作 确保环境准备就绪: 确保你的系统中已安装了Python、Django以及Apache HTTP Server。安装…...
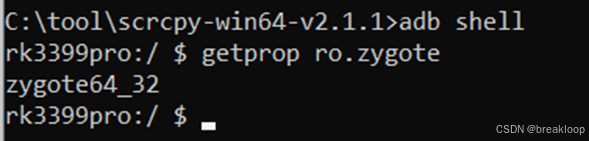
Android Framework学习笔记(4)----Zygote进程
Zygote的启动流程 Init进程启动后,会加载并执行init.rc文件。该.rc文件中,就包含启动Zygote进程的Action。详见“RC文件解析”章节。 根据Zygote对应的RC文件,可知Zygote进程是由/system/bin/app_process程序来创建的。 app_process大致处…...

澎湃算力 玩转AI 华为昇腾AI开发板——香橙派OriengePi AiPro边缘计算案例评测
澎湃算力 玩转AI 华为昇腾AI开发板 香橙派OriengePi AiPro 边缘计算案例评测 人工智能(AI)技术正以前所未有的速度改变着我们的生活、工作乃至整个社会的面貌。作为推动这一变革的关键力量,边缘计算与AI技术的深度融合正成为行业发展的新趋势…...

<数据集>铁轨缺陷检测数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:844张 标注数量(xml文件个数):844 标注数量(txt文件个数):844 标注类别数:3 标注类别名称:[Spalling, Squat, Wheel Burn] 序号类别名称图片数框数1Spalling3315522…...

第2章 矩阵
A 乘以此列向量,1的位置依次往下,所以A的列向量全为0 B C、D 取BE 要统一...
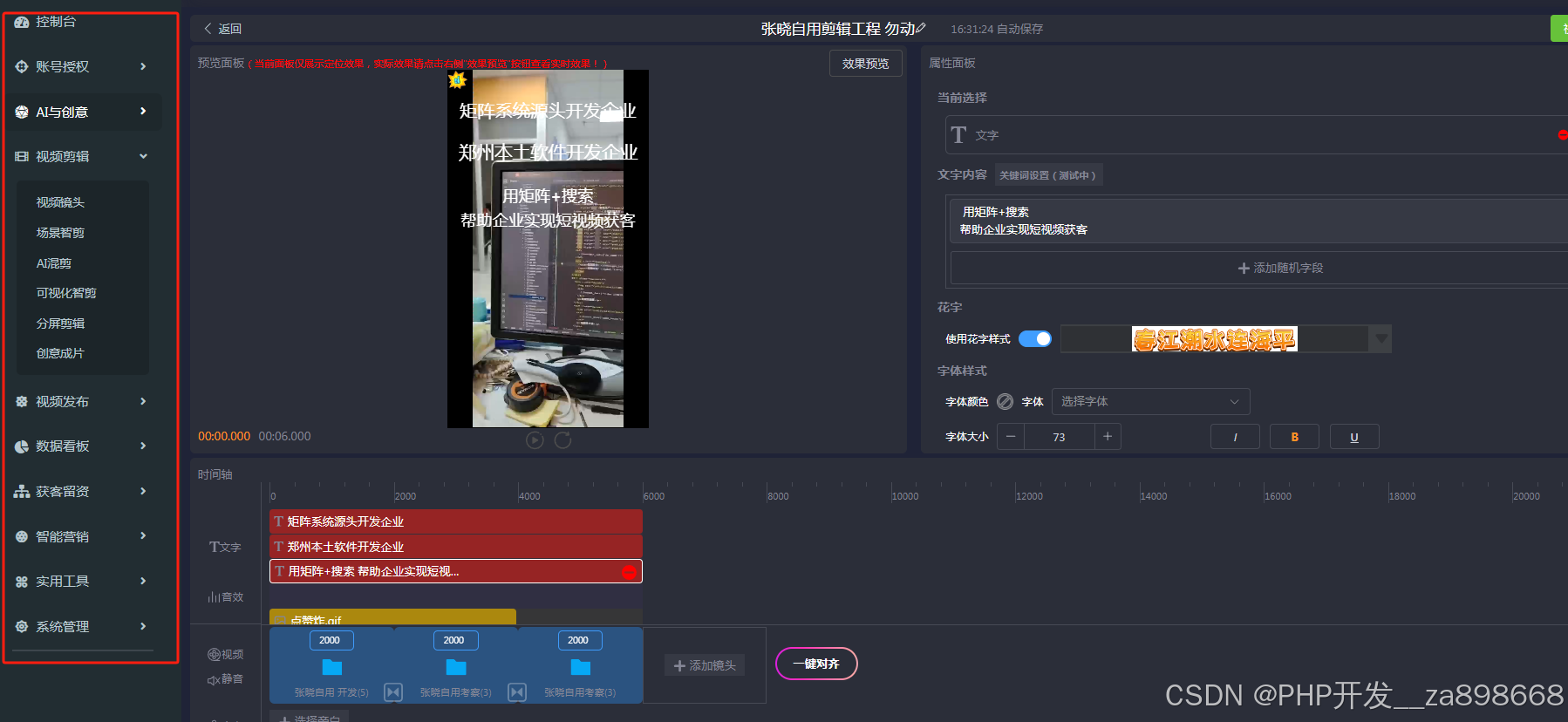
抖音seo短视频矩阵源码系统开发搭建----开源+二次开发
抖音seo短视频矩阵源码系统开发搭建 是一项技术密集型工作,需要对大数据处理、人工智能等领域有深入了解。该系统开发过程中需要用到多种编程语言,如Java、Python等。同时,需要使用一些框架和技术,如Hadoop、Spark、PyTorch等&am…...

【ELK】简述
ELK 堆栈的作用 大规模日志管理与分析 随着系统规模的扩大,应用程序、服务器和网络设备会产生大量的日志数据。ELK 堆栈可以集中收集、存储和索引这些分散在不同服务器和系统中的日志,方便快速检索和分析,帮助您快速定位系统故障、异常事件和…...
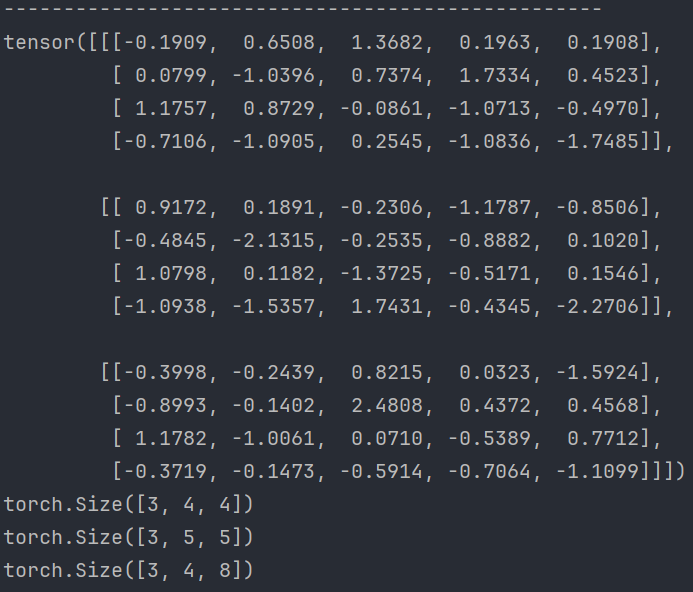
PyTorch张量数值计算
文章目录 1、张量基本运算2、阿达玛积3、点积运算4、指定运算设备⭐5、解决在GPU运行PyTorch的问题 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法&am…...

Dockerfile相关命令
Dockerfile Dockerfile 是一个用来构建Docker镜像的文本文件,包含了一系列构建镜像所需的指令和参数。 指令详解 Dockerfile 指令说明FROM指定基础镜像,用于后续的指令构建,必须为第一个命令MAINTAINER指定Dockerfile的作者/维护者。&…...

【AI教程-吴恩达讲解Prompts】第1篇 - 课程简介
文章目录 简介Prompt学习相关资源 两类大模型原则与技巧 简介 欢迎来到面向开发者的提示工程部分,本部分内容基于吴恩达老师的《Prompt Engineering for Developer》课程进行编写。《Prompt Engineering for Developer》课程是由吴恩达老师与 OpenAI 技术团队成员 I…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
