持续集成04--Jenkins结合Gitee创建项目
前言
在持续集成/持续部署(CI/CD)的旅途中,Jenkins与版本控制系统的紧密集成是不可或缺的一环。本篇“持续集成03--Jenkins结合Gitee创建项目”将引导如何将Jenkins与Gitee(一个流行的Git代码托管平台)相结合,以自动化地处理代码提交后的构建、测试等流程。通过本文,将学会如何在Jenkins中配置Gitee仓库,创建并配置Jenkins项目。
1、新建项目
进入Jenkins首页,点击新建item,输入任务名称,选择Freestyle project,点击确定。

2、项目配置
2.1、源码配置
2.1.1、添加远程仓库地址
新建成功后点击项目配置页(configure)--源码管理(Source Code Management)--Repository URL输入我们Gitee仓库地址。

2.1.2、配置Gitee凭据
选择git;Credentials点击添加,配置gitee凭证

在我们复制Gitee仓库地址时有个提示:安全考虑,建议使用私人令牌;Jenkins凭证常用的有三种:账号密码、api令牌、ssh-key;Git仓库的credentials 只能选择ssh key 或者用户名密码的凭据,gitee api token的凭据只是给触发器用的;所以需要单独为git源码管理插件配置ssh key 或者用户名密码凭据,二者选其一即可。

- 凭证:账号秘密配置
如果不考虑安全的情况下,账号密码配置最为便捷;类型选择username with password,填写gitee的登录账号和密码进行保存

凭证:ssh-key配置
复制服务器git ssh-key公钥:cat /root/.ssh/id_rsa.pub,粘贴到gitee--设置--安全设置SSH公钥内


复制服务器git ssh-key私钥:cat /root/.ssh/id_rsa;Jenkins凭证类型选择ssh,填写git账号名,勾选enter directly,将私钥粘贴到凭证内,保存
注意:如果选择ssh链接,仓库url则需要填写ssh方式


2.1.3、指定构建分支
分支栏为空时默认的是master分支,填写我们需要拉取的分支代码

3、构建项目
配置完成后,点击保存,我们便可以尝试构建项目;点击build now进行项目的构建;点击构建历史--控制台输出可以查看构建进程日志;进入工作空间可以查看拉取代码详情信息



4、执行代码
进入项目配置页--build setps--增加构建步骤--选择Execute shell,编写shell脚本,主要是安装需要的python库和运行程序;保存后,进行构建,查看日志代码执行成功
#!/bin/bash
# 安装项目所需Python库
pip3 install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple/
# 运行程序入口main文件(注意main文件win环境和linux环境的区别)
python3 main_run.py
总结
通过“持续集成03--Jenkins结合Gitee创建项目”的学习,基本成功掌握了将Jenkins与Gitee集成,实现自动化CI/CD流程的关键步骤。Jenkins与Gitee的紧密合作,不仅提高了代码提交后的处理效率,还确保了软件质量的持续监控与提升。现在,每当Gitee仓库中有新的代码提交时,我们都可以通过Jenkins构建、测试等拉取代码,为团队提供了强大的自动化支持。随着对Jenkins与Gitee集成的进一步深入,将能够探索更多高级功能,如代码质量分析、安全扫描等,以全面提升软件开发的效率与质量。
相关文章:

持续集成04--Jenkins结合Gitee创建项目
前言 在持续集成/持续部署(CI/CD)的旅途中,Jenkins与版本控制系统的紧密集成是不可或缺的一环。本篇“持续集成03--Jenkins结合Gitee创建项目”将引导如何将Jenkins与Gitee(一个流行的Git代码托管平台)相结合ÿ…...

【Node.js基础02】fs、path模块
目录 一:fs模块-读写文件 1 加载fs模块对象 2 读制定文件内容文件 3 向文件中写入内容 二:path模块-路径处理 1 问题引入 2 __dirname内置变量 使用方法 一:fs模块-读写文件 fs模块封装了与本机文件系统交互方法和属性 1 加载fs模块…...

牛客TOP101:单链表的排序
文章目录 1. 题目描述2. 解题思路3. 代码实现 1. 题目描述 2. 解题思路 按我们以往的排序算法来看,针对链表来说都是太不合适,因为很多都会出现指针前移后移,后移还好说,前移对于链表来说就太难了,而且大部分都是某一个…...

数据可视化配色新工具,颜色盘多达2500+类
好看的配色,不仅能让图表突出主要信息,更能吸引读者,之前分享过很多配色工具,例如, 👉可视化配色工具:颜色盘多达3000+类,数万种颜色! 本次再分享一个配色工具pypalettes,颜色盘多达2500+类。 安装pypalettes pip install pypalettes pypalettes使用 第1步,挑选…...

SpringAI简单使用(本地模型+自定义知识库)
Ollama 简介 Ollama是一个开源的大型语言模型服务工具,它允许用户在本地机器上构建和运行语言模型,提供了一个简单易用的API来创建、运行和管理模型,同时还提供了丰富的预构建模型库,这些模型可以轻松地应用在多种应用场景中。O…...
为什么要从C语言开始编程
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C语言的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!很多小伙伴在入门编程时。都…...

[数据集][目标检测]导盲犬拐杖检测数据集VOC+YOLO格式4635张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):4635 标注数量(xml文件个数):4635 标注数量(txt文件个数):4635 标注…...

数据结构(稀疏数组)
简介 稀疏数组是一种数据结构,用于有效地存储和处理那些大多数元素都是零或者重复值的数组。在稀疏数组中,只有非零或非重复的元素会被存储,从而节省内存空间。 案例引入 假如想把下面这张表存入文件,我们会怎么做?…...

python 爬虫技术 第02节 基础复习
Python基础复习 Python 是一种高级、通用、解释型的编程语言,以其简洁的语法和强大的功能在数据科学、Web 开发、自动化脚本编写、机器学习等领域广泛使用。下面是一些 Python 基础概念的复习: 1. 数据类型 Python 支持多种内置数据类型,包…...

数据结构-C语言-排序(3)
代码位置:test-c-2024: 对C语言习题代码的练习 (gitee.com) 一、前言: 1.1-排序定义: 排序就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起来。(注:我们这里的排序采用的都为升序) 1.2-排序分…...

【分布式事务】怎么解决分布式场景下数据一致性问题
分布式事务的由来 拿充值订单举个栗子吧,假设:原本订单模块和账户模块是放在一起的,现在需要做服务拆分,拆分成订单服务,账户余额服务。原本收到充值回调后,可以将修改订单状态和扣减余额放在一个mysql事务…...

C# 中的委托
委托的概念 在C#中,委托是一种引用类型,它表示对方法的引用,即委托就是一种用来指向一个方法的引用类型变量。委托的声明类似于方法签名,但是关键字是delegate。下面是一个委托的声明和使用的例子: // 声明一个委托 p…...

通过docker构建基于LNMP的WordPress项目
目录 1.准备nginx 2.准备mysql 3.准备php 4.构建各镜像 5.运行wordpress 1、项目环境: 1.1 (1)公司在实际的生产环境中,需要使用Docker 技术在一台主机上创建LNMP服务并运行Wordpress网站平台。然后对此服务进行相关的性能…...

2024新版IntelliJ IDEA修改包名 全网最简单最粗暴的方法
问题再现 我们在网上淘一些后端框架 又或者是开源的项目 如果要变成自己的 难免会去改包名 即把com.后面的内容改成自己自定义的 第一次我们直接用网络上的方法 shift F6 快捷键 可以修改包名 出现以下情况 进行修改 我们发现失败了 并没有像预计的一样直接把包名修…...

C#中处理Socket粘包
在C#中使用Socket进行网络通信时,粘包问题是常见的。粘包问题通常发生在TCP协议中,因为TCP是流式协议,数据可能会被分割成多个包发送,也可能多个小包会被合并成一个大包接收。 处理粘包问题的常见方法是使用消息分隔符或消息长度…...

7.19IO
思维导图 第一题:测试错误检查锁和递归锁是否会造成死锁状态 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #i…...

【Vue】深入了解 Axios 在 Vue 中的使用:从基本操作到高级用法的全面指南
文章目录 一、Axios 简介与安装1. 什么是 Axios?2. 安装 Axios 二、在 Vue 组件中使用 Axios1. 发送 GET 请求2. 发送 POST 请求 三、Axios 拦截器1. 请求拦截器2. 响应拦截器 四、错误处理五、与 Vuex 结合使用1. 在 Vuex 中定义 actions2. 在组件中调用 Vuex acti…...
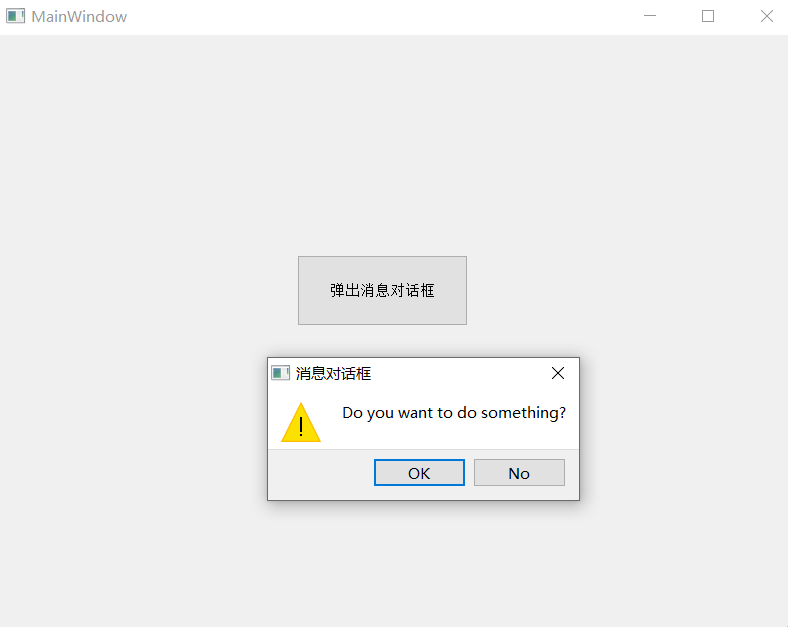
【Qt】窗口
文章目录 QMainWindow菜单栏工具栏状态栏浮动窗口对话框自定义对话框Qt内置对话框QMessageBox QMainWindow Qt中的主窗口以QMainWindow表示,其总体结构如下: 菜单栏 菜单栏MenuBar,可包含多个菜单Menu,每个菜单也可以包含多个菜…...

代码随想录训练营【贪心算法篇】
贪心 注:本文代码来自于代码随想录 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步…...

Spark中的JOIN机制
Spark中的JOIN机制 1、Hash Join概述2、影响JOIN的因素3、Spark中的JOIN机制3.1、Shuffle Hash Join3.2、Broadcast Hash Join3.3、Sort Merge Join3.4、Cartesian Product Join3.5、Broadcast Nested Loop Join4、Spark中的JOIN策略5、Spark JOIN机制与策略总结5.1、Spark中的…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...


