Mad MAD Sum-Codeforces Round 960 (Div. 2)
题目在这里
大意:
MAD函数返回出现次数 ≥ 2 \geq2 ≥2的最大整数
b i b_i bi = M A D ( a [ 1 , 2 , . . . i ] ) MAD(a[1,2,...i]) MAD(a[1,2,...i])
每次操作把 a i a_i ai进行上述操作,直到全变为0为止,对每次操作的数组进行求和,记为 s u m sum sum,问sum的大小
分析:
经过一次运算总可以得到非递减的序列,因为MAD函数非递减,最大值只会越来越大
只有连续的数段可以向右传递,做一次虽然非递减,但是会有只有单个的情况这是不可以向右传递的
我们可以再做一次计算去除这些数,剩下就是可以向右传递的
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;
void calc(vector<int>&a,i64 &s){map<int,int> mp;i64 now = 0;vector<int> res(n+1,0);for(int i = 1;i<=n;++i){mp[a[i]]++;if(mp[a[i]]>=2&&a[i]>now){now = a[i];}res[i] = now;}a = res;for(int i = 1;i<=n;++i){//cout<<a[i]<<' ';s+=a[i];}//cout<<s<<"\n";
}
void solve(){cin>>n;vector<int>a(n+1);i64 s = 0;for(int i = 1;i<=n;++i) cin>>a[i],s+=a[i];calc(a,s);calc(a,s);for(int i = 1;i<=n;++i){s+=(n-i)*1LL*a[i];}//cout<<s<<"\n";
}signed main(){ios;int t;cin>>t;while(t--){solve();}return 0;
}
读错题目了好难受qaq
相关文章:
)
Mad MAD Sum-Codeforces Round 960 (Div. 2)
题目在这里 大意: MAD函数返回出现次数 ≥ 2 \geq2 ≥2的最大整数 b i b_i bi M A D ( a [ 1 , 2 , . . . i ] ) MAD(a[1,2,...i]) MAD(a[1,2,...i]) 每次操作把 a i a_i ai进行上述操作,直到全变为0为止,对每次操作的数组进行求和,记…...

Flutter 插件之 package_info_plus
当使用Flutter开发应用时,通常需要获取应用程序的基本信息,例如包名、版本号和构建号。Flutter提供了一个名为 package_info_plus 的插件,它能方便地帮助我们获取这些信息。 1. 添加依赖 首先,需要在项目的 pubspec.yaml 文件中添加 package_info_plus 的依赖。打开 pubs…...
如何实现布隆过滤器?
1.布隆过滤器的场景 在Redis 缓存击穿(失效)、缓存穿透、缓存雪崩怎么解决?中我们说到可以使用布隆过滤器避免「缓存穿透」。 你会说我们只要记录了每个用户看过的历史记录,每次推荐的时候去查询数据库过滤存在的数据实现去重。 …...

运维团队如何高效监控容器化环境中的PID及其他关键指标
随着云计算和容器化技术的快速发展,越来越多的企业开始采用容器化技术来部署和管理应用程序。然而,容器化环境的复杂性和动态性给运维团队带来了前所未有的挑战。本文将从PID(进程标识符)监控入手,探讨运维团队如何高效…...

通过vue3 + TypeScript + uniapp + uni-ui 实现下拉刷新和加载更多的功能
效果图: 核心代码: <script lang="ts" setup>import { ref, reactive } from vue;import api from @/request/api.jsimport empty from @/component/empty.vueimport { onLoad,onShow, onPullDownRefresh, onReachBottom } from @dcloudio/uni-applet form …...

Pointnet++改进即插即用系列:全网首发WTConv2d大接受域的小波卷积|即插即用,提升特征提取模块性能
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入WTConv2d,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3 步骤三 1.理…...
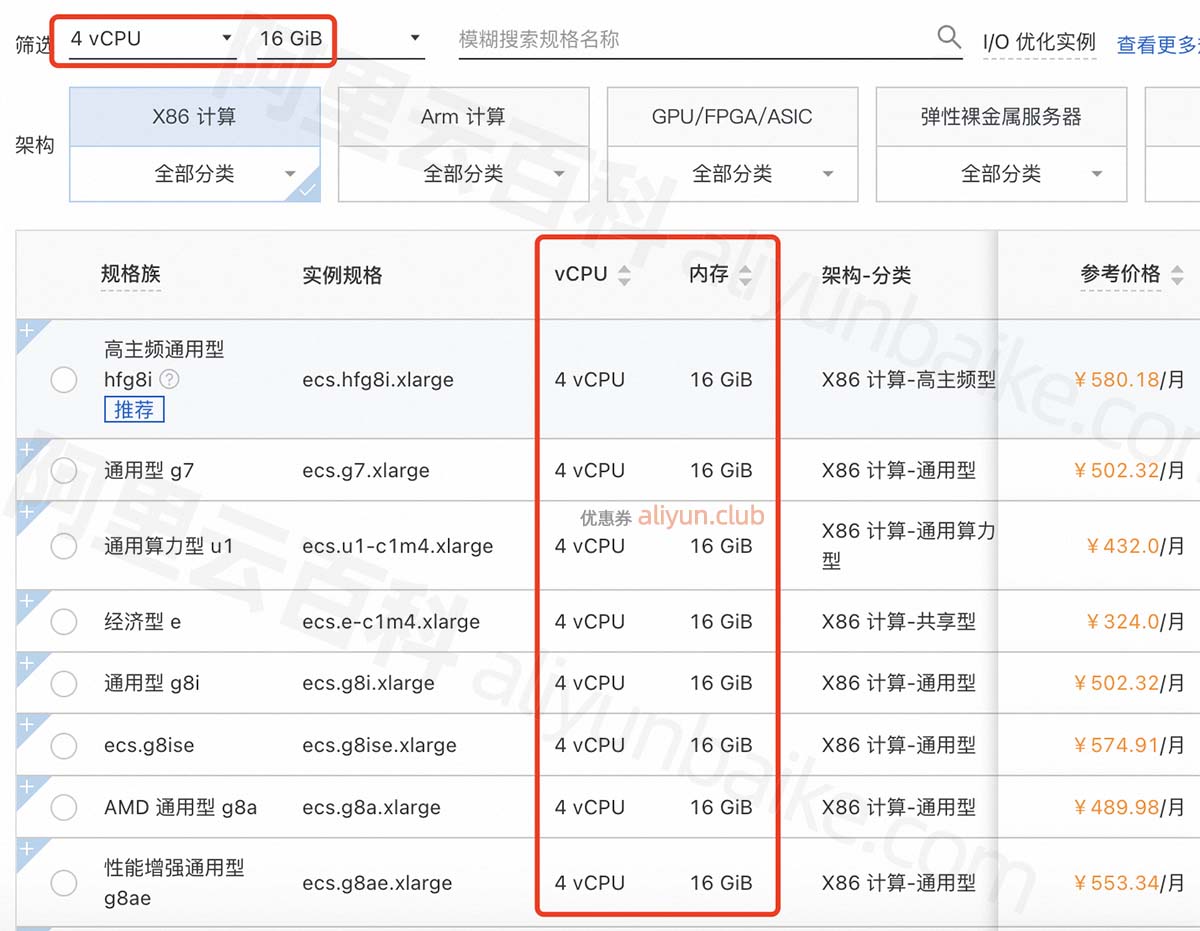
4核16G服务器支持多少人?4C16G服务器性能测评
租赁4核16G服务器费用,目前4核16G服务器10M带宽配置70元1个月、210元3个月,那么能如何呢?配置为ECS经济型e实例4核16G、按固定带宽10Mbs、100GB ESSD Entry系统盘。 那么问题来了,4C16G10M带宽的云服务器可以支持多少人同时在线&…...

塔子哥的平均数-美团2023笔试(codefun2000)
题目链接 塔子哥的平均数-美团2023笔试(codefun2000) 题目内容 给定一个正整数数组a1 ,a2 ,…,an,求平均数正好等于k的最长连续子数组的长度 输入描述 输出描述 输出一个整数,表示最长满足题目条件的长度。 样例1 输入 5 2 1 3 2 4 1 输出 3 样例1解释…...

故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码
故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码 目录 故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于小波包能量谱对滚动轴承的故障诊断 matlab代码 数据采用的是凯斯西储大学数据 首先利用…...

E14.【C语言】练习:有关短路运算
#include <stdio.h> int main() {int i 0,a0,b2,c 3,d4;i a && b && d;printf("a %d\nb %d\nc %d\nd %d\n", a, b, c, d);return 0; } 求输出结果 分析: a:先使用后 ,a(见第15篇http://…...

python BeautifulSoup库安装与使用(anaconda、pip)
BeautifulSoup 是一个可以从HTML或XML文件中提取数据的Python库。Beautiful Soup 已成为和 lxml、html5lib 一样出色的Python解释器,为用户灵活地提供不同的解析策略或强劲的速度。 Requests 获取html BeautifulSoup 解析html、xml,BeautifulSoup4库也称bs4库 安装B…...

基于Matlab的数据可视化
基于Matlab的数据可视化 一、二维图形的绘制(一)基本图形函数(1)plot函数(2)fplot函数(3)其他坐标系的二维曲线 (二)图形属性设置(1)线…...

深入理解Linux网络(二):UDP接收内核探究
深入理解Linux网络(二):UDP接收内核探究 一、UDP 协议处理二、recvfrom 系统调⽤实现 一、UDP 协议处理 udp 协议的处理函数是 udp_rcv。 //file: net/ipv4/udp.c int udp_rcv(struct sk_buff *skb) {return __udp4_lib_rcv(skb, &udp_…...

linux内核中list的基本用法
内核链表 1 list_head 结构 为了使用链表机制,驱动程序需要包含<linux/types.h>头文件,该文件定义了如下结构体实现双向链: struct list_head {struct list_head *next, *prev; };2 链表的初始化 2.1 链表宏定义和初始化 可使用以…...

项目中无关痛痒的词句背后深层含义
项目中听上去无关痛痒的词句背后,深层含义有的时候并不友善。 他们说的:进度表有些激进 真正的意思:我们有麻烦了 他们说的:我们将在接下来的几个迭代里面弥补延误 真正的意思:我们还是有麻烦 他们说的࿱…...
身份验证)
DLMS协议中的高级安全(HLS)身份验证
1.四步身份验证协议 在IEC 62056-53中已说明,ACSE提供部分高级身份安全(HLS)验证服务。高级身份安全验证适用于通信通道不能提供内部安全,应采取防范措施以防止偷听和信息(密码)重现的情况。这时ÿ…...
)
2024“钉耙编程”杭电多校1006 序列立方(思维+前缀和优化dp)
来源 题目 Problem Description 给定长度为 N 的序列 a。 一个序列有很多个子序列,每个子序列在序列中出现了若干次。 小马想请你输出序列 a 每个非空子序列出现次数的立方值的和,答案对 998244353 取模。 你可以通过样例解释来辅助理解题意。 Input 第…...
钡铼分布式I/O系统边缘计算Modbus,MQTT,OPC UA耦合器BL206
BL206系列耦合器是一个数据采集和控制系统,基于强大的32 位微处理器设计,采用Linux操作系统,支持Modbus,MQTT,OPC UA协议,可以快速接入现场PLC、DCS、PAS、MES、Ignition和SCADA以及ERP系统,同时…...

防火墙--双机热备
目录 双击热备作用 防火墙和路由器备份不同之处 如何连线 双机 热备 冷备 VRRP VGMP(华为私有协议) 场景解释 VGMP作用过程 主备的形成场景 接口故障的切换场景 整机故障 原主设备故障恢复的场景 如果没有开启抢占 如果开启了抢占 负载分…...

机器学习 -逻辑回归的似然函数
公式解释 公式如下: L ( θ ) ∏ i 1 m P ( y i ∣ x i ; θ ) ∏ i 1 m ( h θ ( x i ) ) y i ( 1 − h θ ( x i ) ) 1 − y i L(\theta) \prod_{i1}^m P(y_i | x_i; \theta) \prod_{i1}^m (h_\theta(x_i))^{y_i} (1 - h_\theta(x_i))^{1 - y_i} L(θ)i1∏…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
