【C#】计算两条直线的交点坐标
问题描述
计算两条直线的交点坐标,可以理解为给定坐标P1、P2、P3、P4,形成两条线,返回这两条直线的交点坐标?
注意区分:这两条线是否垂直、是否平行。
代码实现
斜率解释
斜率是数学中的一个概念,特别是在解析几何和平面直角坐标系中,用来描述一条直线倾斜程度的量。它定义为直线上任意两点之间的垂直变化量(即纵坐标的变化量,通常称为“上升”或“Δy”)与水平变化量(即横坐标的变化量,通常称为“运行”或“Δx”)之比。斜率通常用字母 m 表示。

需要注意的是,对于垂直线,由于水平变化量“Δx” 为零,所以斜率无法定义,因为这会导致分母为零,我们说垂直线的斜率是无穷大或未定义。
斜率的概念在许多数学和物理问题中都有应用,例如在微积分中,导数可以看作是曲线在某一点处的瞬时斜率;在物理学中,斜率可以表示速度、加速度等随时间的变化率。
在实际应用中,斜率也可以帮助我们理解数据的趋势,比如在统计学中,通过计算散点图中数据点的斜率,我们可以了解变量间的关系是正相关还是负相关。
方法1:两条线不一定垂直
using System;class Program
{struct Point{public double X;public double Y;public Point(double x, double y){X = x;Y = y;}}static Point FindIntersection(Point p1, Point p2, Point p3, Point p4){double a1 = p2.Y - p1.Y;double b1 = p1.X - p2.X;double c1 = a1 * p1.X + b1 * p1.Y;double a2 = p4.Y - p3.Y;double b2 = p3.X - p4.X;double c2 = a2 * p3.X + b2 * p3.Y;double det = a1 * b2 - a2 * b1;if (det == 0){// 两条直线平行或重合,无交点或有无穷多个交点return new Point(double.NaN, double.NaN);}double x = (b2 * c1 - b1 * c2) / det;double y = (a1 * c2 - a2 * c1) / det;return new Point(x, y);}static void Main(){Point p1 = new Point(1, 1);Point p2 = new Point(3, 3);Point p3 = new Point(1, 3);Point p4 = new Point(3, 1);Point intersection = FindIntersection(p1, p2, p3, p4);if (double.IsNaN(intersection.X) && double.IsNaN(intersection.Y)){Console.WriteLine("两条直线平行或重合,无交点或有无穷多个交点");}else{Console.WriteLine($"交点坐标为 ({intersection.X}, {intersection.Y})");}}
}例如,如果 P1(1, 1),P2(3, 3) 代表一条直线,P3(1, 3),P4(3, 1) 代表另一条直线,通过上述代码就能计算出它们的交点坐标。如果两条直线平行,如 P1(1, 1),P2(2, 2) 和 P3(1, 2),P4(2, 1),则返回 (NaN, NaN) 表示无交点。
方法2:两条线垂直
using System;class Program
{struct Point{public double X;public double Y;public Point(double x, double y){X = x;Y = y;}}static Point FindPerpendicularIntersection(Point p1, Point p2, Point p3, Point p4){// 计算两条直线的斜率double slope1 = (p2.Y - p1.Y) / (p2.X - p1.X);double slope2 = (p4.Y - p3.Y) / (p4.X - p3.X);// 如果两条直线中有一条斜率不存在(即垂直于 x 轴)if (double.IsInfinity(slope1)){double x = p1.X;double y = slope2 * (x - p3.X) + p3.Y;return new Point(x, y);}else if (double.IsInfinity(slope2)){double x = p3.X;double y = slope1 * (x - p1.X) + p1.Y;return new Point(x, y);}// 两条直线斜率都存在时double perpendicularSlope1 = -1 / slope1;double perpendicularSlope2 = -1 / slope2;// 计算直线的方程double intercept1 = p1.Y - perpendicularSlope1 * p1.X;double intercept2 = p3.Y - perpendicularSlope2 * p3.X;// 计算交点坐标double x = (intercept2 - intercept1) / (perpendicularSlope1 - perpendicularSlope2);double y = perpendicularSlope1 * x + intercept1;return new Point(x, y);}static void Main(){Point p1 = new Point(1, 1);Point p2 = new Point(3, 3);Point p3 = new Point(1, 3);Point p4 = new Point(3, 1);Point intersection = FindPerpendicularIntersection(p1, p2, p3, p4);if (double.IsNaN(intersection.X) && double.IsNaN(intersection.Y)){Console.WriteLine("两条直线平行或重合,无垂直交点或有无穷多个垂直交点");}else{Console.WriteLine($"垂直交点坐标为 ({intersection.X}, {intersection.Y})");}}
}例如,对于 P1(1, 1),P2(3, 3) 和 P3(1, 3),P4(3, 1) 这组坐标,通过上述代码可以计算出它们的垂直交点坐标。
再比如,如果两条直线平行,如 P1(1, 1),P2(2, 2) 和 P3(1, 2),P4(2, 1),那么将返回 (NaN, NaN) 表示无垂直交点。
相关文章:

【C#】计算两条直线的交点坐标
问题描述 计算两条直线的交点坐标,可以理解为给定坐标P1、P2、P3、P4,形成两条线,返回这两条直线的交点坐标? 注意区分:这两条线是否垂直、是否平行。 代码实现 斜率解释 斜率是数学中的一个概念,特别是…...

在项目服务器部署git 并实现自动提交
以下场景适合在服务器当中使用git 方便提交代码,同时不需要外部的git仓库(码云gitee或者github作为管理平台)。依靠服务器本身ssh 连接协议做为git提交的地址,同时利用钩子自动同步项目代码 首先下载git sudo apt update sudo a…...

前缀匹配工具之IP-Prefix
目录 基本概念: 技术背景: 用户需求: 安全需求: 企业内部的访问控制需求: IP-Prefix的配置与语句分析: 调用方式: 尾声 基本概念: IP-Prefix,即IP前缀,相比传统ACL,它能…...

等级保护测评案例分享及合规建议
一、黑龙江省等级保护测评概述 黑龙江省等级保护测评(简称“等保测评”)是依据国家网络安全等级保护制度的要求,对信息系统进行安全等级划分和安全保护能力的评估。等保测评不仅能够帮助企业和组织发现潜在的安全风险,还能够指导…...

GOLLIE : ANNOTATION GUIDELINES IMPROVE ZERO-SHOT INFORMATION-EXTRACTION
文章目录 题目摘要引言方法实验消融研究 题目 Techgpt-2.0:解决知识图谱构建任务的大型语言模型项目 论文地址:https://arxiv.org/abs/2310.03668 摘要 大型语言模型 (LLM) 与指令调优相结合,在泛化到未见过的任务时取得了重大进展。然而,它…...
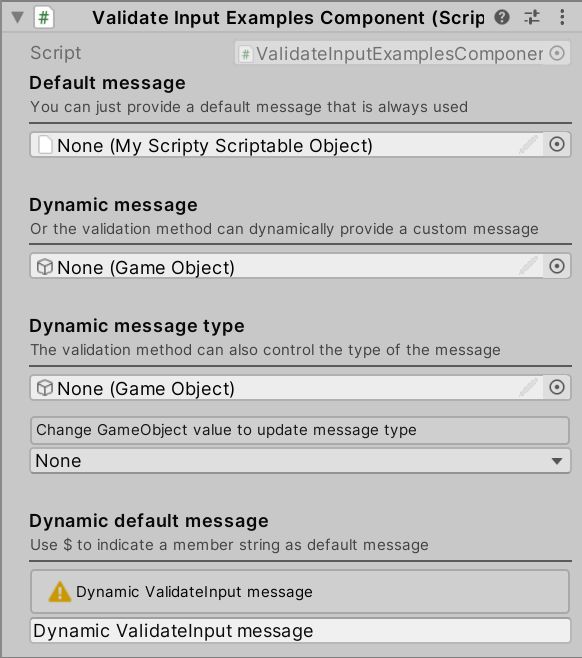
2024-07-19 Unity插件 Odin Inspector9 —— Validation Attributes
文章目录 1 说明2 验证特性2.1 AssetsOnly / SceneObjectsOnly2.2 ChildGameObjectsOnly2.3 DisallowModificationsIn2.4 FilePath2.5 FolderPath2.6 MaxValue / MinValue2.7 MinMaxSlider2.8 PropertyRange2.9 Required2.10 RequiredIn2.11 RequiredListLength2.12 ValidateIn…...

跨平台WPF音乐商店应用程序
目录 一 简介 二 设计思路 三 源码 一 简介 支持在线检索音乐,支持实时浏览当前收藏的音乐及音乐数据的持久化。 二 设计思路 采用MVVM架构,前后端分离,子界面弹出始终位于主界面的中心。 三 源码 视窗引导启动源码: namesp…...
)
设计模式简述(一)
定义:设计模式指的是在软件开发过程中,经过验证的,用于解决在特定环境下,重复出现的,特定问题的解决方案。创建型设计模式关注对象的创建过程,提供了更灵活、可扩展的对象创建机制。结构型设计模式用于解决…...

OSI参考模型:解析网络通信的七层框架
引言 在现代计算机网络中,OSI(开放式系统互联)参考模型是理解和设计网络通信协议的基础。1978年由国际标准化组织(ISO)提出,OSI模型定义了网络通信的七层结构,每一层都承担着特定的功能&#x…...

QT通用配置文件库(QPreferences)
QT通用配置文件库(QPreferences) QPreferences项目是基于nlohmann/json的qt可视化配置文件库,将配置保存成json格式,并提供UI查看与修改,可通过cmake可快速添加进项目。默认支持基本类型、stl常用容器、基本类型与stl容器组成的结构体&#…...

如何搭建一个RADIUS服务器?
1. 系统环境 1.1.操作系统 Ubuntu-20.04.1 (kernel: 5.15.0-58-generic) 1.2.所需软件 FreeRADIUS MariaDB 1.3.注意事项 本文提到的所有操作,都是以root 身份执行; 2. FreeRADIUS的安装 2.1. 安装FreeRADIUS服务器程序 以…...

双机热备综合实验
1,对现有网络进行改造升级,将当个防火墙组网改成双机热备的组网形式,做负载分担模式,游客区和DMZ区走FW3,生产区和办公区的流量走FW1 2,办公区上网用户限制流量不超过100M,其中销售部人员在其基…...

Java和Python的图结构如何实现图的深度优先搜索算法
Java和Python的图结构如何实现图的深度优先搜索算法? 在Java和Python中,实现深度优先搜索(DFS)算法的基本思路都是通过递归或栈来探索图的各个节点。 Java实现DFS:Java import java.util.ArrayList; import java.uti…...

Web学习day05
html&css 目录 html&css 文章目录 一、web开发 1.1工作流程 1.2开发技术 二、HTML 2.1HTML规范 2.2基础标签 2.2.1标题 2.2.2水平线 2.2.3段落和换行 2.2.4文字效果 2.2.5超链接 2.2.6图像 2.2.7音频和视频 三、布局标签 3.1列表 3.2容器 3.3表格 3…...

LINUX客户端client(socket、connect)实现客户端发送,服务器接收
SERVICE端见前一篇文章 5. 客户端连接函数 connect()(与前面的bind一样) int connect (int sockfd, struct sockaddr * serv_addr, int addrlen) 参数: sockfd: 通过 socket() 函数拿到的 fd addr:struct sockaddr 的结构体变量地址 addr…...

【网络安全科普】勒索病毒 防护指南
勒索病毒简介 勒索病毒是一种恶意软件,也称为勒索软件(Ransomware),其主要目的是在感染计算机后加密用户文件,并要求用户支付赎金以获取解密密钥。这种类型的恶意软件通常通过电子邮件附件、恶意链接、下载的软件或漏洞…...

TFHE库,fftw和googletest库安装
点个关注吧!本文主要关注于TFHE的安装与常见的问题 1.TFHE的git链接: https://github.com/tfhe/tfhe git clone --recurse-submodules --branchmaster https://github.com/tfhe/tfhe.git 2.安装 mkdir build cd build cmake ../src -DENABLE_TESTSon -D…...

关于Spring Boot IOCDC,看这一篇就够了
一,Spring是什么及常用注解 先说什么是spring,在前面的博客中已经知道了,spring是一个开源框架,为了让我们开发更加简单,那关于ioc呢,一句话概况一下:Spring就是包含了众多工具方法的Ioc容器 …...

Model Import Settings
前言 在可视化3D世界中,模型是3D世界的核心,你可以没有贴图,可以没有特效,甚至可以没有用户交互界面,但必须得有模型来描述世界的基本样貌。 在3D世界中,由点线面构成了模型的轮廓;由UV和纹理&a…...

腾讯云COS托管静态网站,以及如何解决访问出现了下载网页的情况
腾讯云对象存储(Cloud Object Storage,简称COS),与其他云厂商所提供的云对象存储都是面向非结构化数据,只是每个云厂商的叫法有别于他家,或许是更能彰显厂商的品牌吧! 但不管云厂商怎么给云对象…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
