Math Reference Notes: 数学思想和方法
文章目录
- 1. 数学思想
- 1.1 数形结合思想
- 1.2 转化思想
- 1.3 分类讨论思想
- 1.4 整体思想
- 2. 数学方法
- 2.1 配方法
- 2.2 因式分解法
- 2.3 待定系数法
- 2.4 换元法
- 2.5 构造法
- 2.6 等积法
- 2.7 反证法
- 2.8 判别式法
1. 数学思想
1.1 数形结合思想
定义:将数与形(代数与几何)结合起来,通过图形直观地理解和解决代数问题,或通过代数表达式解决几何问题。
原理:利用图形的直观性和代数的精确性,相互补充,解决复杂问题。
步骤:
- 将代数问题翻译成几何图形。
- 在图形中观察和分析问题。
- 通过图形上的观察得出代数结论,或将几何问题代数化解决。
具体应用:
- 解析几何:通过坐标系将几何问题转化为代数问题。如求解圆的方程 ( x − a ) 2 + ( y − b ) 2 = r 2 (x - a)^2 + (y - b)^2 = r^2 (x−a)2+(y−b)2=r2。
- 函数图像:通过绘制函数图像直观理解函数的性质。如 y = x 2 y = x^2 y=x2 的抛物线图像分析极值和对称性。
- 代数方程:通过绘制二次函数 y = a x 2 + b x + c y = ax^2 + bx + c y=ax2+bx+c 的图像理解方程的根。如 y = x 2 − 4 x + 3 y = x^2 - 4x + 3 y=x2−4x+3 图像与 x 轴交点为方程的解。
示例:
- 解析几何问题:求圆 x 2 + y 2 = 25 x^2 + y^2 = 25 x2+y2=25 与直线 y = 3 x + 7 y = 3x + 7 y=3x+7 的交点。通过代数解法,代入 y = 3 x + 7 y = 3x + 7 y=3x+7 到圆的方程,得到 x 2 + ( 3 x + 7 ) 2 = 25 x^2 + (3x + 7)^2 = 25 x2+(3x+7)2=25,解方程得交点。
- 函数单调性分析:函数 f ( x ) = x 3 − 3 x f(x) = x^3 - 3x f(x)=x3−3x 的单调性,通过图像发现当 x < − 1 x < -1 x<−1 或 x > 1 x > 1 x>1 时函数递增,当 − 1 < x < 1 -1 < x < 1 −1<x<1 时函数递减。
1.2 转化思想
定义:将复杂问题转化为已知问题或更简单的问题,从而更容易解决。
原理:通过引入辅助元素或改变问题的形式,简化问题。
步骤:
- 识别问题的难点。
- 引入辅助元素或方法,将问题转化为已知形式。
- 解决已转化的问题。
- 将解答转换回原问题的解。
具体应用:
- 复杂方程:将高次方程通过换元法转化为低次方程。如 x 4 − 2 x 2 + 1 = 0 x^4 - 2x^2 + 1 = 0 x4−2x2+1=0 转化为 ( x 2 − 1 ) 2 = 0 (x^2 - 1)^2 = 0 (x2−1)2=0。
- 数学建模:将实际问题转化为数学问题。例如,将物理中的运动问题转化为微分方程。
- 不等式:通过代数转化法,如将 a 2 + b 2 ≥ 2 a b a^2 + b^2 \geq 2ab a2+b2≥2ab 转化为 ( a − b ) 2 ≥ 0 (a - b)^2 \geq 0 (a−b)2≥0。
示例:
- 复杂方程:求解方程 x 4 − 5 x 2 + 6 = 0 x^4 - 5x^2 + 6 = 0 x4−5x2+6=0。通过设 y = x 2 y = x^2 y=x2,方程变为 y 2 − 5 y + 6 = 0 y^2 - 5y + 6 = 0 y2−5y+6=0,解得 y = 2 y = 2 y=2 或 y = 3 y = 3 y=3,即 x 2 = 2 x^2 = 2 x2=2 或 x 2 = 3 x^2 = 3 x2=3。
- 几何问题:求两圆 x 2 + y 2 = 16 x^2 + y^2 = 16 x2+y2=16 和 ( x − 4 ) 2 + y 2 = 16 (x - 4)^2 + y^2 = 16 (x−4)2+y2=16 的交点。将两圆的方程相减,得到直线 x = 2 x = 2 x=2,再代入圆的方程解得交点。
1.3 分类讨论思想
定义:根据问题的不同情况进行分类讨论,分别解决。
原理:将一个复杂的问题分解为若干个简单的问题,通过对每个情况的讨论,得出整体结论。
步骤:
- 识别问题中的不同情况或条件。
- 针对每种情况分别讨论和求解。
- 汇总各类情况的解答,得出总解。
具体应用:
- 解方程:如解绝对值方程 ∣ x ∣ = a |x| = a ∣x∣=a 时,需分别讨论 x ≥ 0 x \geq 0 x≥0 和 x < 0 x < 0 x<0 的情况。
- 证明不等式:如在证明三角不等式时,需分别讨论三角形的不同类型(锐角、直角、钝角)。
- 数列求和:如在求解某些数列的通项公式时,需根据不同的项数分类讨论。
示例:
- 绝对值方程:解方程 ∣ x − 2 ∣ = 3 |x - 2| = 3 ∣x−2∣=3。分两种情况讨论:当 x − 2 ≥ 0 x - 2 \geq 0 x−2≥0 时,解 x − 2 = 3 x - 2 = 3 x−2=3 得 x = 5 x = 5 x=5;当 x − 2 < 0 x - 2 < 0 x−2<0 时,解 x − 2 = − 3 x - 2 = -3 x−2=−3 得 x = − 1 x = -1 x=−1。
- 三角不等式:证明三角形的任意两边之和大于第三边。分别讨论三角形的不同类型,通过构造不等式证明。
1.4 整体思想
定义:从整体的角度考虑问题,通过整体和部分之间的关系来解决问题。
原理:把握整体与局部之间的关系,利用整体性质简化局部问题。
步骤:
- 从整体的角度观察问题。
- 分析整体与部分之间的关系。
- 利用整体性质解决局部问题。
具体应用:
- 解方程组:如在解二元一次方程组时,通过整体考虑两个方程的交点。
- 几何证明:如利用整体对称性简化几何图形的证明。
- 数列分析:如在求解数列的极限时,考虑数列的整体趋势。
示例:
- 解方程组:解方程组 { x + y = 3 2 x − y = 1 \begin{cases} x + y = 3 \\ 2x - y = 1 \end{cases} {x+y=32x−y=1。通过整体考虑,消去一个变量,得到 3 x = 4 3x = 4 3x=4,解得 x = 4 3 x = \frac{4}{3} x=34,再代入得到 y = 5 3 y = \frac{5}{3} y=35。
- 几何证明:利用整体对称性证明等腰三角形的两个底角相等。通过整体对称性,证明底边上的中线为角平分线,从而证明底角相等。
2. 数学方法
2.1 配方法
定义:通过配方将一个二次项变成完全平方形式,从而简化计算或解决问题。
原理:利用 ( x + a ) 2 = x 2 + 2 a x + a 2 (x + a)^2 = x^2 + 2ax + a^2 (x+a)2=x2+2ax+a2 的形式,将二次方程化为平方项。
步骤:
- 将二次项提取出来。
- 补全完全平方项。
- 利用完全平方项进行简化或求解。
具体应用:
- 解二次方程:如解 x 2 + 6 x + 5 = 0 x^2 + 6x + 5 = 0 x2+6x+5=0,配方为 ( x + 3 ) 2 − 4 = 0 (x + 3)^2 - 4 = 0 (x+3)2−4=0。
- 标准化:如将椭圆方程 x 2 + y 2 + 6 x − 4 y + 9 = 0 x^2 + y^2 + 6x - 4y + 9 = 0 x2+y2+6x−4y+9=0 配方为 ( x + 3 ) 2 + ( y − 2 ) 2 = 16 (x+3)^2 + (y-2)^2 = 16 (x+3)2+(y−2)2=16。
- 不等式证明:如 x 2 + 6 x + 9 ≥ 0 x^2 + 6x + 9 \geq 0 x2+6x+9≥0 配方为 ( x + 3 ) 2 ≥ 0 (x+3)^2 \geq 0 (x+3)2≥0。
示例:
- 解二次方程:解方程 x 2 + 6 x + 8 = 0 x^2 + 6x + 8 = 0 x2+6x+8=0。通过配方法,配成 ( x + 3 ) 2 − 1 = 0 (x + 3)^2 - 1 = 0 (x+3)2−1=0,解得 x = − 2 x = -2 x=−2 或 x = − 4 x = -4 x=−4。
- 标准化椭圆方程:将椭圆方程 x 2 + 4 x + y 2 − 6 y = 12 x^2 + 4x + y^2 - 6y = 12 x2+4x+y2−6y=12 配成 ( x + 2 ) 2 + ( y − 3 ) 2 = 25 (x+2)^2 + (y-3)^2 = 25 (x+2)2+(y−3)2=25,表示圆心为 ( − 2 , 3 ) (-2, 3) (−2,3),半径为 5 的圆。
2.2 因式分解法
定义:将多项式分解为因式的乘积,从而简化计算或解决方程。
原理:利用
多项式因式分解定理,将多项式表示为若干因式的乘积。
步骤:
- 提取公因式。
- 观察多项式结构,寻找可分解的因式。
- 将多项式表示为因式的乘积。
具体应用:
- 解多项式方程:如 x 3 − 3 x 2 − 4 x + 12 = 0 x^3 - 3x^2 - 4x + 12 = 0 x3−3x2−4x+12=0,因式分解为 ( x − 3 ) ( x + 2 ) ( x − 2 ) = 0 (x-3)(x+2)(x-2) = 0 (x−3)(x+2)(x−2)=0。
- 整式运算:如 x 2 − 4 = ( x + 2 ) ( x − 2 ) x^2 - 4 = (x+2)(x-2) x2−4=(x+2)(x−2)。
- 数学证明:如证明 a 2 − b 2 = ( a + b ) ( a − b ) a^2 - b^2 = (a+b)(a-b) a2−b2=(a+b)(a−b) 的等式。
示例:
- 解多项式方程:解方程 x 3 − 6 x 2 + 11 x − 6 = 0 x^3 - 6x^2 + 11x - 6 = 0 x3−6x2+11x−6=0。因式分解为 ( x − 1 ) ( x − 2 ) ( x − 3 ) = 0 (x-1)(x-2)(x-3) = 0 (x−1)(x−2)(x−3)=0,解得 x = 1 , 2 , 3 x = 1, 2, 3 x=1,2,3。
- 整式运算:简化 x 3 − 3 x 2 − 4 x + 12 x^3 - 3x^2 - 4x + 12 x3−3x2−4x+12。因式分解为 ( x − 3 ) ( x + 2 ) ( x − 2 ) (x-3)(x+2)(x-2) (x−3)(x+2)(x−2)。
2.3 待定系数法
定义:通过设定未知系数,将问题转化为关于这些未知系数的方程,从而求解问题。
原理:利用未知系数构建方程组,通过解方程组确定系数。
步骤:
- 设定未知系数。
- 构建方程组。
- 解方程组确定未知系数。
具体应用:
- 解线性方程组:如 a + b = 1 a + b = 1 a+b=1, 2 a + 3 b = 4 2a + 3b = 4 2a+3b=4。
- 多项式拟合:如求解 f ( x ) = a x 2 + b x + c f(x) = ax^2 + bx + c f(x)=ax2+bx+c 的系数。
- 函数逼近:如利用泰勒展开式逼近函数。
示例:
- 解线性方程组:解方程组 { a + b = 1 2 a + 3 b = 4 \begin{cases} a + b = 1 \\ 2a + 3b = 4 \end{cases} {a+b=12a+3b=4。通过待定系数法,解得 a = − 1 a = -1 a=−1, b = 2 b = 2 b=2。
- 多项式拟合:拟合二次多项式 y = a x 2 + b x + c y = ax^2 + bx + c y=ax2+bx+c 通过 ( 1 , 2 ) (1, 2) (1,2)、 ( 2 , 3 ) (2, 3) (2,3)、 ( 3 , 6 ) (3, 6) (3,6) 三个点。建立方程组,解得 a , b , c a, b, c a,b,c 的值。
2.4 换元法
定义:通过引入新的变量,将复杂问题转化为更简单的问题来解决。
原理:利用变量替换,将问题转化为标准形式或已知形式。
步骤:
- 识别问题中的复杂部分。
- 引入新的变量替换复杂部分。
- 转化为简单问题求解。
- 将解答转换回原问题的解。
具体应用:
- 积分计算:如 ∫ sin 2 x d x \int \sin^2 x \, dx ∫sin2xdx,通过换元 u = cos x u = \cos x u=cosx 简化。
- 解方程:如 x 4 − 2 x 2 + 1 = 0 x^4 - 2x^2 + 1 = 0 x4−2x2+1=0 通过 y = x 2 y = x^2 y=x2 转化为 y 2 − 2 y + 1 = 0 y^2 - 2y + 1 = 0 y2−2y+1=0。
- 函数分析:如研究 f ( x ) = 1 x 2 + 1 f(x) = \frac{1}{x^2 + 1} f(x)=x2+11 的性质,通过 y = x 2 y = x^2 y=x2 转化为 g ( y ) = 1 y + 1 g(y) = \frac{1}{y + 1} g(y)=y+11。
示例:
- 积分计算:计算 ∫ sin 2 x d x \int \sin^2 x \, dx ∫sin2xdx。通过换元 u = cos x u = \cos x u=cosx, d u = − sin x d x du = -\sin x \, dx du=−sinxdx,积分变为 ∫ ( 1 − u 2 ) ( − d u ) \int (1 - u^2) (-du) ∫(1−u2)(−du),解得积分结果。
- 解方程:解方程 x 4 − 4 x 2 + 3 = 0 x^4 - 4x^2 + 3 = 0 x4−4x2+3=0。通过设 y = x 2 y = x^2 y=x2,方程变为 y 2 − 4 y + 3 = 0 y^2 - 4y + 3 = 0 y2−4y+3=0,解得 y = 1 y = 1 y=1 或 y = 3 y = 3 y=3,即 x 2 = 1 x^2 = 1 x2=1 或 x 2 = 3 x^2 = 3 x2=3。
2.5 构造法
定义:通过构造特定的例子或对象来证明或反驳一个命题。
原理:通过具体的构造过程,验证命题的正确性或错误性。
步骤:
- 识别问题需要验证的命题。
- 构造特定的例子或对象。
- 通过构造验证命题。
具体应用:
- 数论:如构造满足条件的数来证明命题。
- 几何问题:如构造特定图形验证几何性质。
- 概率问题:如构造特定事件计算概率。
示例:
- 数论:证明存在无穷多个质数。假设有有限个质数 p 1 , p 2 , … , p n p_1, p_2, \ldots, p_n p1,p2,…,pn,构造数 N = p 1 p 2 ⋯ p n + 1 N = p_1 p_2 \cdots p_n + 1 N=p1p2⋯pn+1,则 N N N 不是已有质数的倍数,矛盾,故有无穷多个质数。
- 几何问题:证明平行四边形对角线互相平分。构造平行四边形 A B C D ABCD ABCD,通过坐标法验证其对角线互相平分。
2.6 等积法
定义:通过等积变换来简化计算或证明命题,尤其在几何问题中常用。
原理:利用等积变换保持面积不变,简化问题。
步骤:
- 识别需要保持面积不变的图形。
- 进行等积变换。
- 利用变换后的图形进行计算或证明。
具体应用:
- 面积计算:如利用割补法计算复杂图形的面积。
- 几何证明:如证明三角形面积不变性。
- 优化问题:如通过等积变换寻找最优解。
示例:
- 面积计算:计算梯形面积。将梯形通过割补法变为矩形,利用矩形的面积公式计算梯形面积。
- 几何证明:证明两等高三角形面积相等。通过平移或旋转变换,使两个三角形等积,从而证明面积相等。
2.7 反证法
定义:通过假设结论不成立,然后推导出矛盾,从而证明结论的成立。
原理:通过矛盾推理,验证命题的正确性。
步骤:
- 假设结论不成立。
- 根据假设推导出矛盾。
- 通过矛盾证明结论成立。
具体应用:
- 数学证明:如证明数论中的命题。
- 几何证明:如证明图形的某些性质。
- 存在性问题:如证明某些解的存在性。
示例:
- 数学证明:证明 (\sqrt{2}) 不是有理数。假设 (\sqrt{2}) 是有理数,则可表示为最简分数 a b \frac{a}{b} ba,则 2 b 2 = a 2 2b^2 = a^2 2b2=a2,可得 a a a 和 b b b 同时为偶数,与最简分数矛盾,故 (\sqrt{2}) 不是有理数。
- 几何证明:证明直角三角形斜边的中线等于斜边的一半。假设不等,构造矛盾证明结论成立。
2.8 判别式法
定义:通过多项式的判别式来判断多项式的根的性质。
原理:利用二次多项式的判别式 Δ = b 2 − 4 a c \Delta = b^2 - 4ac Δ=b2−4ac 判断根的数量和性质。
步骤:
- 计算判别式。
- 根据判别式的值判断根的性质。
- 解方程或不等式。
具体应用:
- 解二次方程:如 x 2 + 2 x + 1 = 0 x^2 + 2x + 1 = 0 x2+2x+1=0,判别式 Δ = 0 \Delta = 0 Δ=0 有一重根。
- 高次方程:如分析三次方程根的分布。
- 不等式证明:如判断二次函数在某
区间上的取值范围。
示例:
- 解二次方程:解方程 x 2 − 4 x + 4 = 0 x^2 - 4x + 4 = 0 x2−4x+4=0。判别式 Δ = 0 \Delta = 0 Δ=0,方程有一重根,解为 x = 2 x = 2 x=2。
- 高次方程:分析方程 x 3 − 3 x 2 + 2 x = 0 x^3 - 3x^2 + 2x = 0 x3−3x2+2x=0 的根。通过判别式判断根的分布,解得根为 x = 0 , 1 , 2 x = 0, 1, 2 x=0,1,2。
相关文章:

Math Reference Notes: 数学思想和方法
文章目录 1. 数学思想1.1 数形结合思想1.2 转化思想1.3 分类讨论思想1.4 整体思想 2. 数学方法2.1 配方法2.2 因式分解法2.3 待定系数法2.4 换元法2.5 构造法2.6 等积法2.7 反证法2.8 判别式法 1. 数学思想 1.1 数形结合思想 定义:将数与形(代数与几何…...
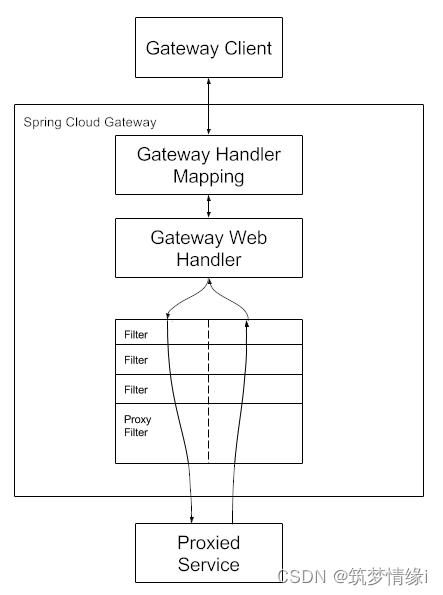
Spring Cloud GateWay(4.1.4)
介绍 该项目提供了一个建立在 Spring 生态系统之上的 API 网关,包括:Spring 6、Spring Boot 3 和 Project Reactor。Spring Cloud Gateway 旨在提供一种简单而有效的方法来路由到 API,并为其提供跨领域关注点,例如:安…...
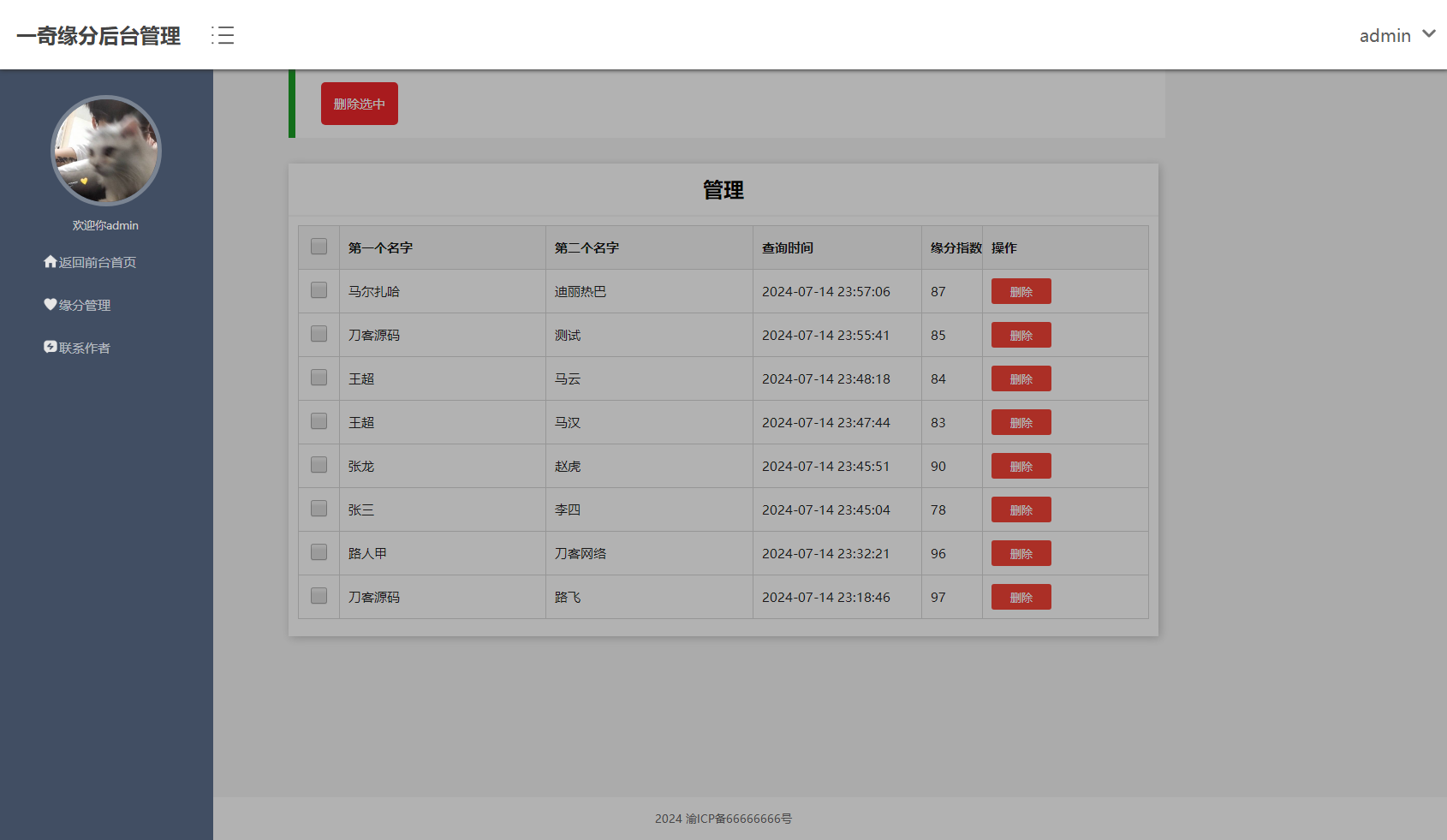
基于PHP+MYSQL开发制作的趣味测试网站源码
基于PHPMYSQL开发制作的趣味测试网站源码。可在后台提前设置好缘分, 自己手动在数据库里修改数据,数据库里有就会优先查询数据库的信息, 没设置的话第一次查询缘分都是非常好的 95-99,第二次查就比较差 , 所以如果要…...

【微信小程序】wx.navigateTo传参时不能使用const定义的数据类型
2024年7月21日更新 今日调试时发现似乎是因为使用vant-weapp时按照官方提示关闭了style:"v2"导致的此情况,打开之后无法复现该内容,特此提示。 以下是原内容 如题,笔者测试了好久才找到这个bug,想传递的数据是this.d…...

【Android studio环境搭建】Android studio连接夜神模拟器
Android studio连接夜神模拟器 一、 步骤 1.下载好Android Studio和夜神模拟器, 2.打开夜神模拟器,找到其安装目录下的 nox_adb.exe文件 3.右键进入cmd命令打开,管理员权限执行下面命令 PS D:\Program Files\Nox\bin> .\nox_adb.exe connect 127.…...

Qt:26.Qt项目:贪吃蛇游戏
一、项目功能演示: 开始界面可以点击进入游戏。 点击进入游戏之后,切换到选项界面,该界面可以选择游戏难度,回退,以及查询最近一次游戏得分。 游戏具体界面如下。贴图啥的可以自己换,本人审美不咋行&#x…...

通过HTML/CSS 实现各类进度条的功能。
需求:我们在开发中会遇到使用各式各样的进度条,因为当前插件里面进度条各式各样的,为了方便我们定制化的开发和方便修改样式,我们这里使用HTML和CSS样式来进行开发进度条功能。 通过本文学习我们会明白如何使用 HTML/CSS 创建各种…...

Opencv学习项目3——人脸识别
之前我们获取了一张图像的人脸信息,现在我们来使用特征点分析来匹配两张lyf照片的相似度 获取两张图片的人脸信息 import cv2 import face_recognition# 加载图像文件 img1 face_recognition.load_image_file(lyf1.png) img2 face_recognition.load_image_file(l…...
的使用总结+代码举例)
【js自学打卡11】生成器函数(generator函数)的使用总结+代码举例
力扣的js入门免费题刷完了,开始自己找题练练,顺便捡捡知识点 力扣2649 1.思路 一眼递归,但事实证明也可以直接flat手撕。 arr.flat(Infinity) //直接扁平化到最底层涉及到了一些关于生成器和异步编程相关的知识点,学一下。 2.…...

深入了解jdbc-02-CRUD
文章目录 操作和访问数据库Statement操作数据表的弊端sql注入问题PreparedStatement类ResultSet类与ResultSetMetaData类资源的释放批量插入 操作和访问数据库 数据库的调用的不同方式: Statement:用于执行静态 SQL 语句并返回它所生成结果的对象。PreparedStatem…...
《基于 Kafka + Quartz 实现时限质控方案》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…...

浏览器的卡顿与react的解决思路
以下内容是阅读过程中结合自己的思考而诞生的产物,不一定准确,但相反的,可能个人对实际情况有很大的误解。 仅做参考,欢迎指正。 前面提到浏览器显示的其实是渲染流程最后渲染出来的一张图片,而一个行为引起的副作用需…...

XXE:XML外部实体引入
XXE漏洞 如果服务器没有对客户端的xml数据进行限制,且版本较低的情况下,就可能会产生xxe漏洞 漏洞利用流程 1.客户端发送xml文件,其中dtd存在恶意的外部实体引用 2.服务器进行解析 3.服务器返回实体引用内容 危害:任意文件读…...

3D培训大师创新培训体验,加速空调关键组件的高效精准安装
如今,空调系统的复杂性和精密性与日俱增,对专业技术人员的要求也日益提高。尤其是决定空调是否能平稳运行的空调关键组件的装配培训,不再局限于传统的理论讲解和实体模型演示,而是更注重数字化、沉浸式学习。 案例背景 某空调公…...

PyTorch 深度学习实践-循环神经网络(高级篇)
视频指路 参考博客笔记 参考笔记二 文章目录 上课笔记总代码练习 上课笔记 个人能力有限,重看几遍吧,第一遍基本看不懂 名字的每个字母都是一个特征x1,x2,x3…,一个名字是一个序列 rnn用GRU 用ASCII表作为词典,长度为128&#x…...

这才是老板喜欢的电子信息类简历
点击可直接使用...

MySQL学习之事务,锁机制
事务 什么是事务? 事务就是逻辑上的一组操作,要么全做,要么全不做 事务经典例子:转账,转账需要两个操作,从一个人账户上减钱,在另一个账户上加钱,比如说小红给小明转账100元&…...

开源知识付费小程序源码 内容付费系统php源码 含完整图文部署教程
在当今数字化时代,知识付费作为一种新型的经济模式,正逐渐受到越来越多内容创作者、专家及商家的青睐。开源知识付费小程序源码和内容付费系统PHP源码作为实现这一模式的重要工具,为构建高效、安全、可扩展的知识付费平台提供了强大的技术支持…...

时序数据库如何选型?详细指标总结!
工业物联网场景,如何判断什么才是好的时序数据库? 工业物联网将机器设备、控制系统与信息系统、业务过程连接起来,利用海量数据进行分析决策,是智能制造的基础设施,并影响整个工业价值链。工业物联网机器设备感知形成了…...

【前端】JavaScript入门及实战51-55
文章目录 51 函数52 函数的参数53 返回值54 练习55 return 51 函数 <!DOCTYPE html> <html> <head> <title></title> <meta charset "utf-8"> <script type"text/javascript">/* 函数:1. 函数也是…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
