E17.【C语言】练习:sizeof和strlen的辨析
先回顾http://t.csdnimg.cn/aYHl6
1.
char acX[] = "abcdefg";
char acY[] = { 'a','b','c','d','e','f','g'};以下说法正确的是( )
A.数组acX和数组acY等价
B.数组acX和数组acY的长度相同
C.sizeof(acX)>sizeof (acY)
D.strlen (acX)>strlen (acY)
分析:A.数组等价的定义:类型一样,表达式相同,显然:字符串以\0结束,而单个字符没有,需要程序向后读取 A不选
B,D.acY[]长度未知,'g'后\0的出现是随机的,因此strlen (acX)>或=strlen (acY),B,D不选
C.sizeof这里求的是数组大小,数组大小等于有效元素(含\0)的个数*每个元素的大小,sizeof(acX) = 8*4=32,sizeof(acY) = 7*4=28(默认4字节) 选C
2.下面代码的结果是:( )
#include <stdio.h>
int main()
{char str[] = "hello bit";printf("%d %d\n", sizeof(str), strlen(str));return 0;
}分析:hello bit\0
sizeof()算\0,strlen()不算\0
结果:10 9
相关文章:

E17.【C语言】练习:sizeof和strlen的辨析
先回顾http://t.csdnimg.cn/aYHl6 1. char acX[] "abcdefg"; char acY[] { a,b,c,d,e,f,g}; 以下说法正确的是( ) A.数组acX和数组acY等价 B.数组acX和数组acY的长度相同 C.sizeof(acX)>sizeof (acY) D.strlen (acX)>strlen (acY) 分析:…...

便携气象站:科技助力气象观测
在科技飞速发展的今天,便携气象站以其轻便、高效、全面的特点,正逐渐改变着气象观测的传统模式。这款小巧而强大的设备,不仅为气象学研究和气象灾害预警提供了有力支持,更为户外活动、农业生产等领域带来了诸多便利。 便携气象站是…...

php 存储复杂的json格式查询(如:经纬度)
在开发中,有时我们可能存了一些复杂json格式不知道怎么查。我这里提供给大家参考下: 一、先上表数据格式(location字段的possiton经纬度以逗号分开的) {"title":"澳海文澜府","position":"11…...

UDP网口(1)概述
文章目录 1.计算机网络知识在互联网中的应用2.认识FPGA实现UDP网口通信3.FPGA实现UDP网口通信的方案4.FPGA实现UDP网口文章安排5.传送门 1.计算机网络知识在互联网中的应用 以在浏览器中输入淘宝网为例,介绍数据在互联网是如何传输的。我们将要发送的数据包称作A&a…...

Linux - 进程的概念、状态、僵尸进程、孤儿进程及进程优先级
进程基本概念 课本概念:在编程或软件工程的上下文中,进程通常被视为正在执行的程序的实例。当你启动一个应用程序时,操作系统会为这个程序创建一个进程。每个进程都有自己的独立内存空间,可以运行自己的指令序列,并可能…...

Gradle依赖报告:项目依赖树的X光机
Gradle依赖报告:项目依赖树的X光机 在复杂的软件项目中,依赖管理是确保应用正常构建和运行的关键。Gradle作为一个强大的构建工具,提供了依赖报告功能,帮助开发者分析和理解项目的依赖树。本文将详细介绍如何在Gradle中使用依赖报…...
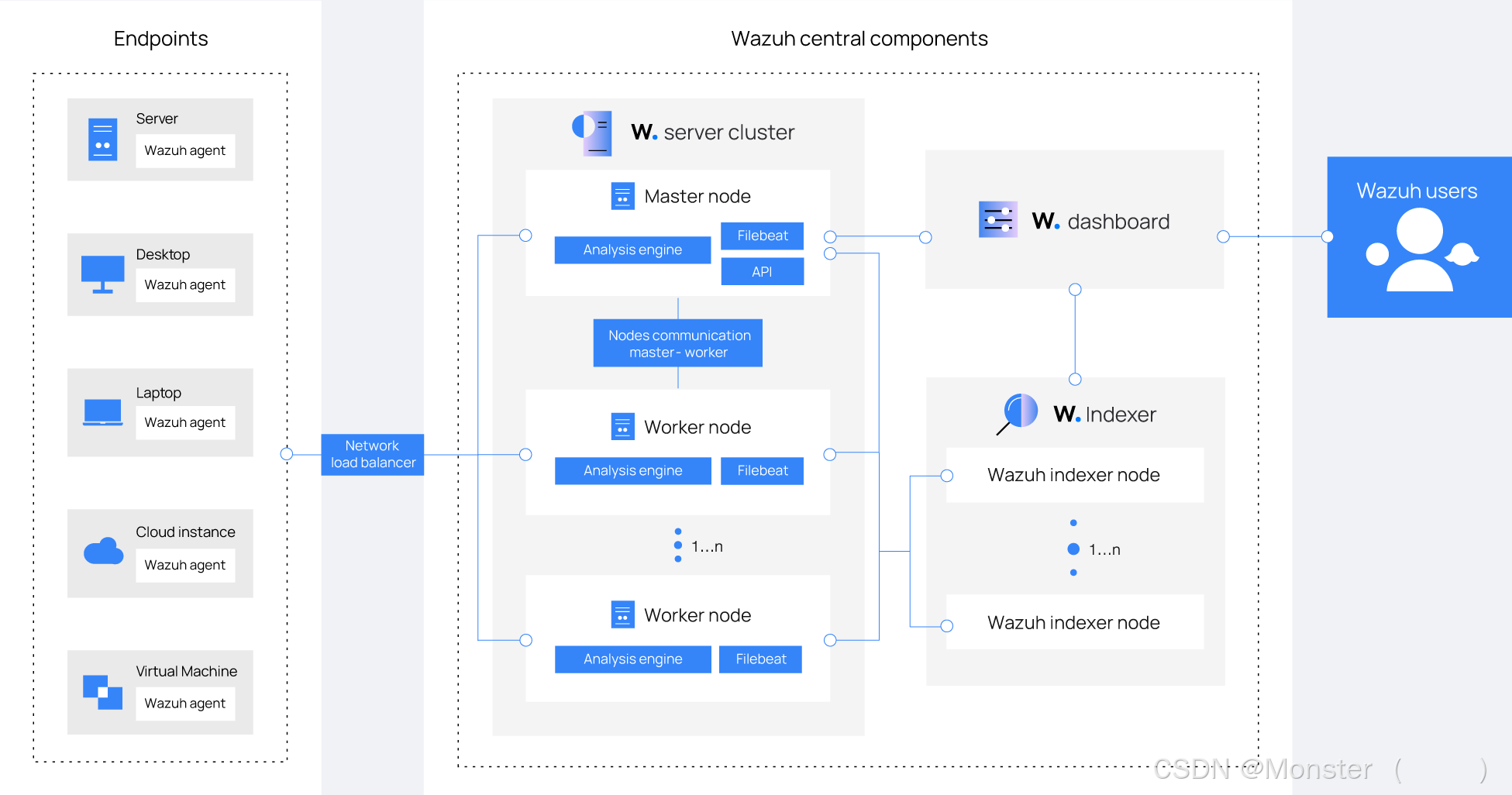
开源XDR-SIEM一体化平台 Wazuh (1)基础架构
简介 Wazuh平台提供了XDR和SIEM功能,保护云、容器和服务器工作负载。这些功能包括日志数据分析、入侵和恶意软件检测、文件完整性监控、配置评估、漏洞检测以及对法规遵从性的支持。详细信息可以参考Wazuh - Open Source XDR. Open Source SIEM.官方网站 Wazuh解决…...
)
从零开始:构建基于深度学习的实时跌倒检测系统(UI界面+YOLO代码+数据集)
注意看文末的结局与声明 一、引言 1. 项目背景与动机 在老年人和高危职业环境中,跌倒是一种常见的事故,可能导致严重的伤害甚至致命。实时跌倒检测系统可以及时发现并报警,提供紧急救助。通过深度学习技术,可以提高跌倒检测的准…...

【策略模式在项目中的实际应用】
业务场景 最最近项目中有这样的一个业务场景: 用户下单->管理员审核->配送员接单->配送中->送达–>签收->完成 整个业务以这种流程的形式存在,每个流程状态的业务不一样,考虑到多种状态如果直接写一个接口肯定会嵌套太多…...
昇思25天学习打卡营第14天|计算机视觉
昇思25天学习打卡营第14天 文章目录 昇思25天学习打卡营第14天FCN图像语义分割语义分割模型简介网络特点数据处理数据预处理数据加载训练集可视化 网络构建网络流程 训练准备导入VGG-16部分预训练权重损失函数自定义评价指标 Metrics 模型训练模型评估模型推理总结引用 打卡记录…...

将json数组格式转成数组
start cmd [ 27 01 f7 01 24 38 02 b7 42 6e ee 2f 69 46 72 21 74 44 c4 22 7a 92 d8 6a de 66 61 b1 1e 2f de ee 5c 31 57 db df 01 31 2d c9 01 01 c0 FB ] set_ulpk {“jsonrpc”:“2.0”,“type”:2,“id”:0,“method”:“method”,“message”:{“VALUE”:[56,2,183,66…...
接口测试之测试原则、测试用例、测试流程详解
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 一、接口的介绍 软件测试中,常说的接口有两种:图形用户接口(GUI,人与程序的接口)、应用程序编程接口&…...
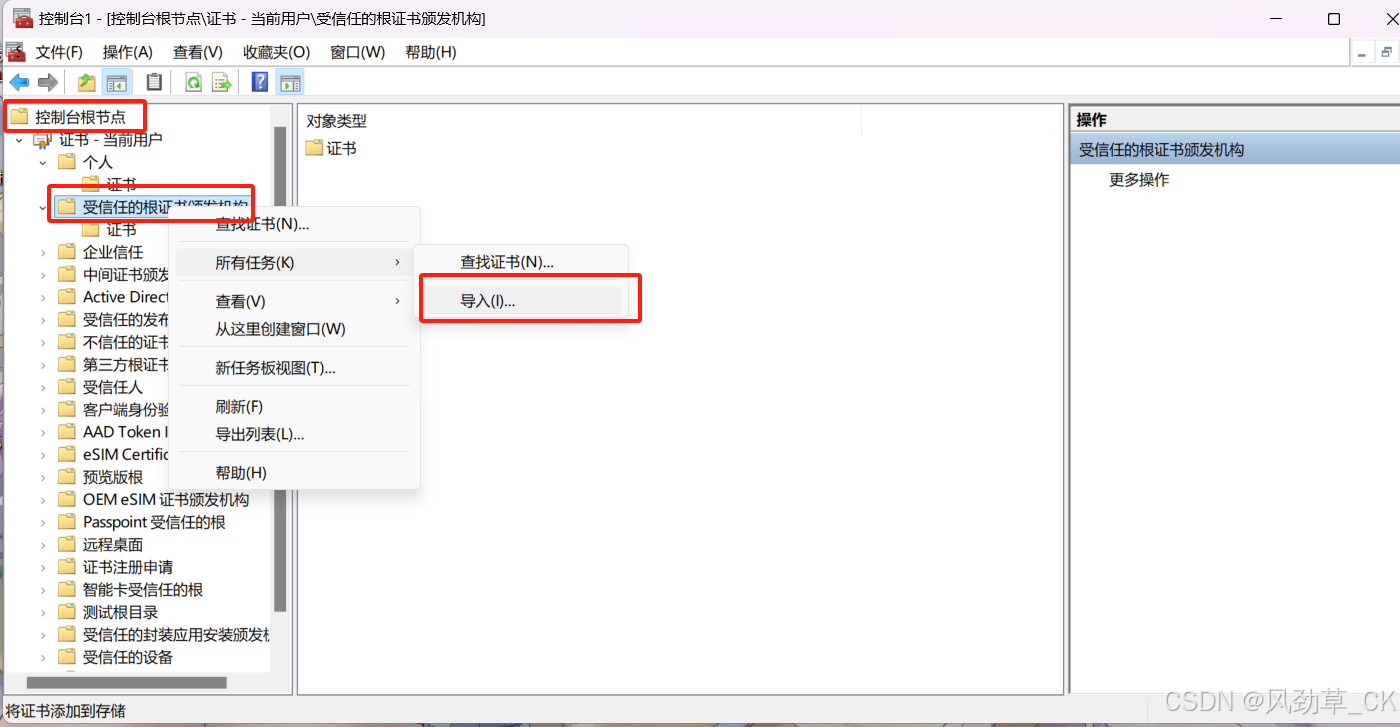
证书上的服务器名错误解决方法
方法 win r ,输入mmc 点击文件——>添加/删除管理单元 找到证书——> 添加 根据自己的存放选择存放位置 点击控制台根节点——> 受信任的根证书颁发机构——>导入 若还出现问题,则参考https://blog.csdn.net/mm120138687/article/details/…...

前端:上传2进制图片
1、let formData new FormData(); 2、添加要传的字段:formData.append("avatarfile", data); (key,value) 3、上传文件 function uploadImg() {// 1定义FormDatalet formData new FormData();// 2添加字段formData.append("…...
)
web前端 React 框架面试200题(三)
面试题 65. 在使用 React Router时,如何获取当前页面的路由或浏览器中地址栏中的地址? 参考回答: 在当前组件的 props中,包含 location属性对象,包含当前页面路由地址信息,在 match中存储当前路由的参数等…...

交流负载箱:电力系统的节能利器
交流负载箱是模拟电网中实际负载的装置,它能够精确地模拟各种电器设备的耗电情况,为电力系统的节能提供了重要的工具。在电力系统中,交流负载箱的应用非常广泛,它可以用于电力系统的设计、运行和维护,以及电力设备的测…...

【思科】链路聚合实验配置和背景
【思科】链路聚合实验配置和背景 背景链路聚合基本概念链路聚合聚合接口 思科链路聚合协议01.PAgP协议02.LACP协议 思科链路聚合模式LACP协议模式PAgP协议模式ON模式 实验准备配置二层链路聚合LACP协议模式SW1SW2PC1PC2查看LACP聚合组建立情况查看LACP聚合端口情况查看逻辑聚合…...

使用 vue-element-plus-admin 框架遇到的问题记录
项目打包遇到的问题: 打包语句:pnpm run build:pro 报错信息: Error: [vite]: Rollup failed to resolve import "E:/workplace_gitee/xxx/node_modules/.pnpm/element-plus2.5.5_vue3.4.15/node_modules/element-plus/es/components…...

从零开始手写STL库:List
从零开始手写STL库–List部分 Github链接:miniSTL 文章目录 从零开始手写STL库–List部分List是什么?List需要包含什么函数1)基础成员函数2)核心功能3)其他功能 基础成员函数的编写核心功能的编写其他功能编写总结 List是什么&am…...

蒙特卡洛采样
目录 蒙特卡洛采样的计算逻辑计算步骤:1. 定义问题2. 确定采样范围3. 生成随机样本点4. 计算函数值5. 估计期望值或积分值6. 计算误差具体示例:1. 定义问题2. 确定采样范围3. 生成随机样本点4. 计算函数值5. 估计积分值6. 计算误差总结蒙特卡洛采样是一种通过随机生成样本点来…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
