数学建模--图论与最短路径
目录
图论与最短路径问题
最短路径问题定义
常用的最短路径算法
Dijkstra算法
Floyd算法
Bellman-Ford算法
SPFA算法
应用实例
结论
延伸
如何在实际应用中优化Dijkstra算法以提高效率?
数据结构优化:
边的优化:
并行计算:
稀疏矩阵和向量运算:
代码优化:
Floyd算法在处理多源最短路径问题时的具体实现步骤是什么?
Bellman-Ford算法如何检测并处理负权边的图中的负环?
SPFA算法与Bellman-Ford算法相比有哪些优势和局限性?
优势
局限性
在网络通信领域,图论及其算法解决最短路径问题的最新研究进展是什么?
在数学建模中,图论及其算法在解决最短路径问题上具有重要应用。图论是研究图及其性质的学科,而图中的节点和边代表了现实世界中的各种元素及其相互关系。
图论与最短路径问题
最短路径问题定义
最短路径问题是指在给定的带权有向或无向图中,寻找两个顶点之间的路径,使得这条路径上的边权重之和最小。该问题广泛应用于交通规划、物流配送、网络通信等领域。
常用的最短路径算法
-
Dijkstra算法
- 特点:Dijkstra算法是一种典型的单源最短路径算法,适用于非负权有向图。它通过贪心策略逐步扩展最短路径树,直到覆盖所有节点。
- 基本步骤:
- 将所有顶点标记为未访问。
- 初始化源点到自身的距离为0,到其他所有顶点的距离为无穷大。
- 选择当前未访问的顶点中距离源点最近的顶点作为当前顶点,并更新其相邻顶点的距离值。
- 当前顶点被标记为已访问后,重复上述过程,直到所有顶点都被访问。
import heapqdef dijkstra(graph, start):"""graph: 邻接表形式的图,例:{0: {1: 10, 2: 3}, 1: {2: 1, 3: 2}, 2: {1: 4, 3: 8}, 3: {}}start: 起始节点返回每个节点到起始节点的最短路径距离"""priority_queue = []heapq.heappush(priority_queue, (0, start))distances = {node: float('inf') for node in graph}distances[start] = 0while priority_queue:current_distance, current_node = heapq.heappop(priority_queue)if current_distance > distances[current_node]:continuefor neighbor, weight in graph[current_node].items():distance = current_distance + weightif distance < distances[neighbor]:distances[neighbor] = distanceheapq.heappush(priority_queue, (distance, neighbor))return distances# 示例使用 graph = {0: {1: 10, 2: 3},1: {2: 1, 3: 2},2: {1: 4, 3: 8},3: {} } start_node = 0 print(dijkstra(graph, start_node))
-
Floyd算法
- 特点:Floyd算法用于求解所有顶点对之间的最短路径问题,即多源最短路径问题。它通过动态规划的方法逐步更新各顶点对之间的最短路径。
- 基本步骤:
- 初始化一个矩阵,其中包含图中所有顶点对的初始距离。
- 对于每一个中间顶点k,更新所有顶点对(i, j)的距离:d[i][j] = min(d[i][j], d[i][k] + d[k][j])。
- 重复上述过程,直到所有中间顶点都被考虑过,最终得到所有顶点对之间的最短路径。
def floyd_warshall(graph):"""graph: 邻接矩阵形式的图,例:[[0, 3, float('inf'), 5], [2, 0, float('inf'), 4], [float('inf'), 1, 0, float('inf')], [float('inf'), float('inf'), 2, 0]]返回所有节点对之间的最短路径距离"""num_vertices = len(graph)dist = list(map(lambda i: list(map(lambda j: j, i)), graph))for k in range(num_vertices):for i in range(num_vertices):for j in range(num_vertices):dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])return dist# 示例使用 graph = [[0, 3, float('inf'), 5],[2, 0, float('inf'), 4],[float('inf'), 1, 0, float('inf')],[float('inf'), float('inf'), 2, 0] ] print(floyd_warshall(graph))
-
Bellman-Ford算法
特点:Bellman-Ford算法可以处理带负权边的图,并且能够检测出图中是否存在负环。其基本思想是利用松弛操作不断更新各顶点的最短路径估计值,直到没有进一步改进为止。
def bellman_ford(graph, start):"""graph: 边列表形式的图,例:[(0, 1, 10), (0, 2, 3), (1, 2, 1), (1, 3, 2), (2, 1, 4), (2, 3, 8)]start: 起始节点返回每个节点到起始节点的最短路径距离和是否存在负权环"""num_vertices = len({u for u, v, w in graph}.union({v for u, v, w in graph}))distances = {i: float('inf') for i in range(num_vertices)}distances[start] = 0for _ in range(num_vertices - 1):for u, v, w in graph:if distances[u] != float('inf') and distances[u] + w < distances[v]:distances[v] = distances[u] + w# 检测负权环for u, v, w in graph:if distances[u] != float('inf') and distances[u] + w < distances[v]:return distances, Truereturn distances, False# 示例使用 graph = [(0, 1, 10), (0, 2, 3), (1, 2, 1), (1, 3, 2), (2, 1, 4), (2, 3, 8)] start_node = 0 print(bellman_ford(graph, start_node)) -
SPFA算法
特点:SPFA算法是Bellman-Ford算法的一种改进版本,通过维护一个队列来减少重复操作次数,从而提高效率。它同样适用于带负权边的图。
from collections import dequedef spfa(graph, start):"""graph: 邻接表形式的图,例:{0: {1: 10, 2: 3}, 1: {2: 1, 3: 2}, 2: {1: 4, 3: 8}, 3: {}}start: 起始节点返回每个节点到起始节点的最短路径距离和是否存在负权环"""num_vertices = len(graph)distances = {node: float('inf') for node in graph}in_queue = {node: False for node in graph}count = {node: 0 for node in graph}distances[start] = 0queue = deque([start])in_queue[start] = Truewhile queue:u = queue.popleft()in_queue[u] = Falsefor v, weight in graph[u].items():if distances[u] + weight < distances[v]:distances[v] = distances[u] + weightcount[v] += 1if count[v] >= num_vertices:return distances, True # 存在负权环if not in_queue[v]:queue.append(v)in_queue[v] = Truereturn distances, False# 示例使用 graph = {0: {1: 10, 2: 3},1: {2: 1, 3: 2},2: {1: 4, 3: 8},3: {} } start_node = 0 print(spfa(graph, start_node))
应用实例
在实际应用中,图论及其算法被广泛用于解决各种优化问题。例如,在旅行商问题(TSP)中,需要找到访问所有城市一次并返回起点的最短路径;在物流配送中,需要找到从仓库到各个配送点的最短路线以节省成本和时间。
结论
图论在数学建模中的应用非常广泛,特别是在解决最短路径问题方面。通过Dijkstra、Floyd、Bellman-Ford等算法,我们可以有效地求解单源或多源最短路径问题,从而在交通规划、物流管理、网络通信等多个领域发挥重要作用。
延伸
如何在实际应用中优化Dijkstra算法以提高效率?
在实际应用中,为了优化Dijkstra算法以提高效率,可以采取以下几种方法:
数据结构优化:
- 使用优先队列(如最小堆)来替代传统的数组或列表。这可以显著减少每次迭代时寻找最短路径节点的时间复杂度,从而提高整体效率。
- 具体来说,可以使用二叉堆或斐波那契堆等高效的数据结构来实现优先队列,这样可以在每次迭代中快速找到当前距离源点最近的节点。
边的优化:
- 链式前向星和vector实现邻接表是两种常见的优化边的方法。链式前向星适用于稀疏图,而vector邻接表则适用于稠密图。
- 这些方法通过减少边的存储和访问时间,提高了算法的运行效率。
并行计算:
- 使用多核处理器并行计算,例如在Matlab中使用parfor循环代替传统的for循环,这样可以利用多核处理器的优势来加速计算。
- 另外,也可以考虑使用GPU加速,特别是在处理大规模数据时,这将大大提升算法的运算速度。
稀疏矩阵和向量运算:
- 在程序中使用稀疏矩阵可以减少计算量和内存占用,特别适合处理大规模图数据。
- 使用向量运算代替循环,可以进一步提高计算速度。这种方法在某些编程环境中(如Matlab)尤其有效。
代码优化:
- 对于具体的实现,可以通过代码优化来提高效率。例如,在Java中,可以使用堆优化版的Dijkstra算法,并提供详细的代码示例和解释。
Floyd算法在处理多源最短路径问题时的具体实现步骤是什么?
Floyd算法在处理多源最短路径问题时的具体实现步骤如下:
初始化邻接矩阵:首先,需要一个n×n的邻接矩阵D来存储所有顶点对之间的最短距离。初始时,将矩阵中的所有元素设为无穷大(表示没有直接连接),除了对角线上的元素(即每个点到自身的距离),这些都设为0。
遍历所有中间节点:接下来,遍历所有的中间节点k(从0到n-1)。对于每一个中间节点k,再遍历所有顶点对(i, j),检查通过节点k是否可以找到一条比已知路径更短的路径。
更新最短路径:对于每一对顶点(i, j),计算通过当前中间节点k的路径长度,并与已知的路径长度进行比较。如果新的路径长度更短,则更新D矩阵中的(i, j)值,并更新指针数组P,记录中间节点k的信息。
重复上述过程:重复上述步骤,直到所有中间节点都被考虑过。这样,最终的D矩阵将包含所有顶点对之间的最短路径长度。
输出结果:最后,根据D矩阵和指针数组P,可以输出任意两点之间的最短路径及其长度。
Bellman-Ford算法如何检测并处理负权边的图中的负环?
Bellman-Ford算法是一种用于解决单源最短路径问题的算法,特别适用于包含负权边的图。然而,该算法不能处理负权环,因为如果存在负权环,则可以不断通过环来减小路径长度,从而导致最短路径计算不收敛。
为了检测并处理负权边的图中的负环,Bellman-Ford算法在求解最短路径后,会进行一次额外的循环(即第n次循环)。这个额外的循环的目的是检查是否存在一个环,其权重之和小于零。具体步骤如下:
初始化距离数组:首先,初始化所有顶点的距离值。源点到自身的距离设为0,其他所有顶点到源点的距离设为无穷大。
执行n-1次松弛操作:对每条边进行松弛操作,以更新最小距离。这一步骤重复执行n-1次,其中n是顶点的数量。每次松弛操作都会尝试通过当前边来更新某个顶点的最短距离。
执行第n次松弛操作:在完成上述n-1次松弛操作之后,再次遍历所有的边,并尝试通过这些边来进一步更新顶点的距离值。如果在这一步骤中发现有顶点的最短距离被更新了,则说明存在一个负权环。
返回结果:如果在第n次松弛操作中没有发现任何顶点的距离被更新,则说明不存在负权环;否则,存在负权环。
总结来说,Bellman-Ford算法通过在求解最短路径后的额外循环来检测图中是否存在负权环。
SPFA算法与Bellman-Ford算法相比有哪些优势和局限性?
SPFA算法(Shortest Path Faster Algorithm)是基于Bellman-Ford算法的优化版本,具有一定的优势和局限性。以下是详细的比较:
优势
SPFA算法的时间复杂度为O(kE),其中k为所有顶点进队的平均次数,通常情况下k远小于V(顶点数),因此在实际应用中,其运行时间较Bellman-Ford算法更短。
在稀疏图上,SPFA算法的效率显著高于Dijkstra算法和Bellman-Ford算法。这是因为SPFA通过队列机制减少了重复操作的次数,从而提高了整体效率。
尽管SPFA算法在某些情况下表现不如Bellman-Ford算法,但其仍然能够有效处理负权回路问题。
相比于Bellman-Ford算法,SPFA算法不需要初始化极大的数,只需初始化为0即可,这可以减少大量的搜索工作量。
局限性
在稠密图中,SPFA算法的表现不如Bellman-Ford算法的Yem氏优化版本。当一个点入队次数超过边的次数时,需要辅助数组统计各点入队次数,导致空间与时间效率低下。
SPFA算法的时间复杂度虽然理论上为O(kE),但在不同图中的表现差异较大,且尚未严格证明其时间复杂度,因此在实际应用中无法准确估计其运行时间。
虽然SPFA算法相对于Bellman-Ford算法有所改进,但其内存消耗仍然较大,特别是在处理大规模数据时,二维数组的使用会增加额外的内存负担。
SPFA算法在处理稀疏图和无向图时具有明显的优势,并且在负权回路问题的处理上也表现良好。然而,它在稠密图中的表现不佳,且时间复杂度不稳定,内存消耗较大。
在网络通信领域,图论及其算法解决最短路径问题的最新研究进展是什么?
在网络通信领域,图论及其算法在解决最短路径问题方面取得了显著的进展。近年来的研究主要集中在以下几个方面:
随着网络环境的不断变化,传统的静态图算法已经无法满足需求。因此,研究者们提出了基于2-hopCOVER的TOP-K最短路径算法,该算法适用于动态有向带权图,并且能够高效地处理大规模图中的实时变化。
蚁群法是一种模拟自然界蚂蚁觅食行为的启发式算法,被广泛应用于旅行商模型(TSP)和树模型的最小生成树问题中。通过这些方法,可以有效地构建出具有最少成本的网络拓扑结构。
自动化软件定义网络(SDN)技术为卫星网络的最短路径优化提供了新的解决方案。通过利用SDN的灵活性和可编程性,研究人员开发了专门针对卫星网络环境的最短路径优化算法,以提高数据传输效率和网络性能。
经典的图论算法如Dijkstra、Bellman-Ford、SPFA和Floyd等在无向连通图的最小生成树问题、最短路径问题以及网络最大流、最小流和最小费用最大流等问题上仍然具有重要的应用价值。这些算法不仅在理论上有深入研究,在实际应用中也得到了广泛的推广和使用。
图论方法在通信网的路由选择规划和流量分配优化方面也发挥了重要作用。通过建立通信网络的图论模型和矩阵描述方法,可以实现对路由选择和最短路径的有效计算,从而优化整个网络的性能。
图染色算法在通信网络中也有重要应用,例如通过图染色可以实现多路径传输以避免冲突和拥塞。此外,还有许多其他高级算法如最大流算法、最小费用流算法等被用于不同场景下的网络优化。
相关文章:

数学建模--图论与最短路径
目录 图论与最短路径问题 最短路径问题定义 常用的最短路径算法 Dijkstra算法 Floyd算法 Bellman-Ford算法 SPFA算法 应用实例 结论 延伸 如何在实际应用中优化Dijkstra算法以提高效率? 数据结构优化: 边的优化: 并行计算&…...

FLINK-checkpoint失败原因及处理方式
在 Flink 或其他分布式数据处理系统中,Checkpoint 失败可能由多种原因引起。以下是一些常见的原因: 资源不足: 如果 TaskManager 的内存或磁盘空间不足,可能无法完成状态的快照,导致 Checkpoint 失败。 网络问题&am…...

Hbase映射为Hive外表
作者:振鹭 Hbase对应Hive外表 (背景:在做数据ETL中,可能原始数据在列式存储Hbase中,这个时候,如果我们想清洗数据,可以考虑把Hbase表映射为Hive的外表,然后使用Hive的HQL来清除处理数据) 1. …...
题解)
洛谷P1002(过河卒)题解
题目传送门 思路 直接爆搜会TLE,所以考虑进行DP。 由于卒只可以从左边和上面走,所以走到(i,j)的路程总数为从上面走的路程总数加上从左边走的路程总数。我们用dp[i][j]表示从起点走到(i,j)的路程总数,那么状态转移方程为: dp[…...

微信小程序 async-validator 表单验证 第三方包
async-validator 是一个基于 JavaScript 的表单验证库,支持异步验证规则和自定义验证规则 主流的 UI 组件库 Ant-design 和 Element 中的表单验证都是基于 async-validator 使用 async-validator 可以方便地 构建表单中逻辑,使得错误提示信息更加友好和灵…...

马克·扎克伯格解释为何开源AI对开发者有利
Meta 今天发布了 Llama 3.1 系列人工智能模型,在人工智能领域取得了重大进展,其性能可与领先的闭源模型相媲美。值得一提的是,在多项人工智能基准测试中,Llama 3.1 405B 模型的性能超过了 OpenAI 的 GPT-4o 和 Claude 3.5 Sonnet。…...

游戏外挂的技术实现与五年脚本开发经验分享
引言: 在数字娱乐的浪潮中,电子游戏成为许多人生活中不可或缺的一部分。然而,随着游戏的普及,一些玩家为了追求更高效的游戏体验或不正当竞争优势,开始使用游戏外挂程序。这些外挂往往通过修改游戏正常运行机制来提供非…...
认识神经网络【多层感知器数学原理】
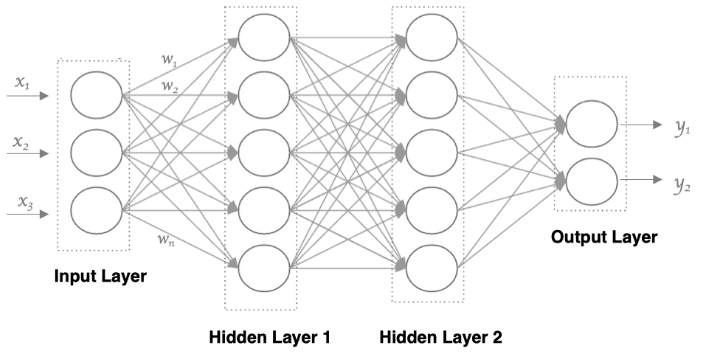
文章目录 1、什么是神经网络2、人工神经网络3、多层感知器3.1、输入层3.2、隐藏层3.2.1、隐藏层 13.2.2、隐藏层 2 3.3、输出层3.4、前向传播3.4.1、加权和⭐3.4.2、激活函数 3.5、反向传播3.5.1、计算梯度3.5.2、更新权重和偏置 4、小结 🍃作者介绍:双非…...

MySQL入门学习-SQL高级技巧.CTE和递归查询
在 MySQL 中,SQL 高级技巧包括了 Common Table Expressions(CTE)和递归查询等。 一、CTE(Common Table Expressions,公共表表达式)的概念: CTE 是一个临时的结果集,它可以在一个查询…...

键盘是如何使用中断机制的?当打印一串字符到显示屏上时发生了什么???
当在键盘上按下一个键时会进行一下操作: 1.当按下任意一个键时,键盘编码器监控会来判断按下的键是哪个 2.键盘控制器用将解码,将键盘的数据保存到键盘控制器里数据寄存器里面 3.此时发送一个中断请求给中断控制器,中断控制器获取到中断号发送…...

Spring Boot 接口访问频率限制的实现详解
目录 概述为什么需要接口访问频率限制常见的实现方式 基于过滤器的实现基于拦截器的实现基于第三方库Bucket4j的实现 实际代码示例 基于过滤器实现Rate Limiting基于拦截器实现Rate Limiting使用Bucket4j实现Rate Limiting 最佳实践 选择合适的限流算法优化性能记录日志和监控…...

前端页面:用户交互持续时间跟踪(duration)user-interaction-tracker
引言 在用户至上的时代,精准把握用户行为已成为产品优化的关键。本文将详细介绍 user-interaction-tracker 库,它提供了一种高效的解决方案,用于跟踪用户交互的持续时间,并提升项目埋点的效率。通过本文,你将了解到如…...
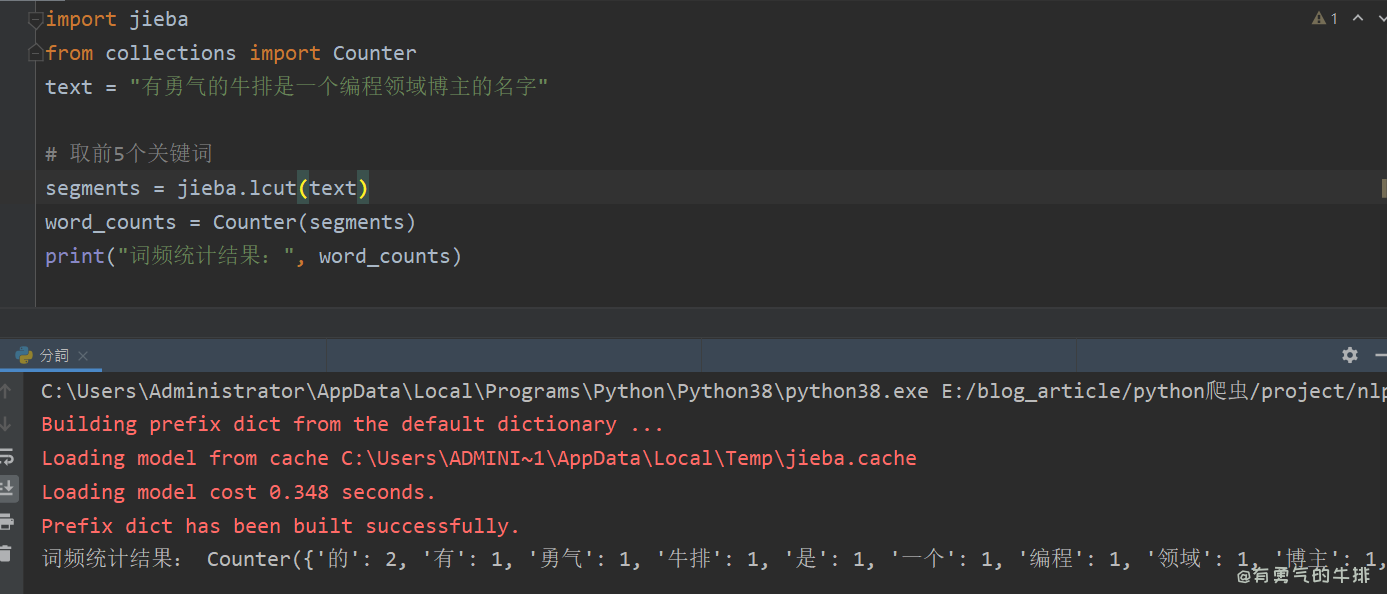
中文分词库 jieba 详细使用方法与案例演示
1 前言 jieba 是一个非常流行的中文分词库,具有高效、准确分词的效果。 它支持3种分词模式: 精确模式全模式搜索引擎模式 jieba0.42.1测试环境:python3.10.9 2 三种模式 2.1 精确模式 适应场景:文本分析。 功能࿱…...

EXO-helper解释
目录 helper解释 helper解释 在Python中,字符串 "\033[93m" 是一个ANSI转义序列,用于在支持ANSI转义码的终端或控制台中改变文本的颜色。具体来说,\033[93m 用于将文本颜色设置为亮黄色(或浅黄色,具体取决于终端的显示设置)。 这里的 \033 实际上是八进制的 …...

Qt开发网络嗅探器01
引言 随着互联网的快速发展和普及,人们对网络性能、安全和管理的需求日益增长。在复杂的网络环境中,了解和监控网络中的数据流量、安全事件和性能问题变得至关重要。为了满足这些需求,网络嗅探器作为一种重要的工具被 广泛应用。网络嗅探器是…...
)
mysql面试(三)
MVCC机制 MVCC(Multi-Version Concurrency Control) 即多版本并发控制,了解mvcc机制,需要了解如下这些概念 事务id 事务每次开启时,都会从数据库获得一个自增长的事务ID,可以从事务ID判断事务的执行先后…...

阿里云公共DNS免费版自9月30日开始限速 企业或商业场景需使用付费版
本周阿里云发布公告对公共 DNS 免费版使用政策进行调整,免费版将从 2024 年 9 月 30 日开始按照请求源 IP 进行并发数限制,单个 IP 的请求数超过 20QPS、UDP/TCP 流量超过 2000bps 将触发限速策略。 阿里云称免费版的并发数限制并非采用固定的阈值&…...

捷配生产笔记-一文搞懂阻焊层基本知识
什么是阻焊层? 阻焊层(也称为阻焊剂)是应用于PCB表面的一层薄薄的聚合物材料。其目的是保护铜电路,防止焊料在焊接过程中流入不需要焊接的区域。除焊盘外,整个电路板都涂有阻焊层。 阻焊层应用于 PCB 的顶部和底部。树…...

html 常用css样式及排布问题
1.常用样式 <style>.cy{width: 20%;height: 50px;font-size: 30px;border: #20c997 solid 3px;float: left;color: #00cc00;font-family: 黑体;font-weight: bold;padding: 10px;margin: 10px;}</style> ①宽度(长) ②高度(宽&a…...

【SpingCloud】客户端与服务端负载均衡机制,微服务负载均衡NacosLoadBalancer, 拓展:OSI七层网络模型
客户端与服务端负载均衡机制 可能有第一次听说集群和负载均衡,所以呢,我们先来做一个介绍,然后再聊服务端与客户端的负载均衡区别。 集群与负载均衡 负载均衡是基于集群的,如果没有集群,则没有负载均衡这一个说法。 …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
