【数据结构】建堆算法复杂度分析及TOP-K问题
【数据结构】建堆算法复杂度分析及TOP-K问题

🔥个人主页:大白的编程日记
🔥专栏:数据结构
文章目录
- 【数据结构】建堆算法复杂度分析及TOP-K问题
- 前言
- 一.复杂度分析
- 1.1向下建堆复杂度
- 1.2向上建堆复杂度
- 1.3堆排序复杂度
- 二.TOP-K问题
- 2.1思路分析
- 2.2代码实现
- 后言
前言
哈喽,各位小伙伴大家好!上期我们讲了堆排序和建堆算法。今天我们就来分析一下他们的时间复杂度。话不多说,咱们进入正题。向大厂冲锋!
一.复杂度分析
我们都知道堆是一个完全二叉树。那他的高度h和节点数量N有什么关系呢?

那我们再来对比一下满二叉树和完全二叉树的高度h.

我们用大O渐进表示法看的话他们两个的高度h都可以认为是logN的量级
所以我们的堆的上下调整可以认为是logN,也就是高度次。
因为堆是完全二叉树,而满二叉树也是完全二叉树,所以为了方便证明
我们使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个结点不影响最终结果):
1.1向下建堆复杂度
我们先分别算出第一层到h-1层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

1.2向上建堆复杂度
我们先分别算出第2层到h层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

所以向下建堆的时间复杂度是O(N),向上建堆的复杂度是O(N*logN).
所以以后我们都尽量使用向下调整建堆。因为他的效率更高。
1.3堆排序复杂度
现在我们来看一下我们堆排序的时间复杂度是多少呢?
- 推导

堆排序的复杂度是O(N*logN).
二.TOP-K问题
2.1思路分析
我们的堆除了可以用来排序还可以用来解决经典的TOP-K问题。
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
- 方法一
我们很容易想到直接排序然后取出前K个即可。
但是这个方法有个致命缺陷。
如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

我们发现这个方法在数据量太大的时候并不适用。
那有什么其他好的方法吗? - 方法二
最佳的方式就是用堆来解决,基本思路如下:
1 .用数据集合中前K个元素来建堆
前k个最大的元素,则建K个数的小堆
前k个最小的元素,则建K个数的大堆
2 . 用剩余的N-K个元素依次与堆顶元素来比较,
如果比堆顶元素还要大或小(小堆大 大堆小)则替换堆顶元素,然后向下调整重新建堆。
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
为什么呢?
- 证明

我们通过N-K次比较就可以筛选出N-K个不满足最大前K个数的数
剩下在堆的数就是最大的前K个。 - 疑问

我们用反证法可以得知这种情况不存在。
2.2代码实现
- 生成数据函数
我们先用srand生成不同的种子防止生成的随机数是伪随机数。
然后fopen打开文件。循环生成随机数然后写入文件即可。最后关闭文件。
void CreatData()
{int n = 100000;//生成10万个数据srand(time(0));//生成不同的种子FILE* pf = fopen("test.txt", "w");//打开文件for (int i = 0; i < n; i++){int x = rand() % 100001+i;//生成随机数fprintf(pf, "%d\n", x);//写数据}fclose(pf);//关闭文件pf = NULL;
}

这样10万个数据就生成好了。
- 比较函数
我们先接收k。然后开好k个数是堆空间。
然后从文件读取前k个数并填充到堆里面。然后建堆
然后继续读取文件里的数据直到文件末尾(返回EOF)
然后当数据大于堆顶元素是在进堆,然后重新调整建堆即可。
void test()
{int k;printf("请输入前K个数:");scanf("%d", &k);int* a = (int*)malloc(sizeof(int) * k);//开空间建堆FILE* pf = fopen("test.txt", "r");for (int i = 0; i < k; i++){fscanf(pf, "%d", &a[i]);}//填充数据for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, k, i);}//建小堆int x;while (fscanf(pf, "%d", &x) !=EOF){if (x > a[0]){a[0] = x;AdjustDown(a, k, 0);}}//对比for (int i = 0; i < k; i++){printf("%d ", a[i]);}//打印
}
- 检验

那我们如何确保这10个数一定是最大的呢?万一我们的算法写错不是最大的前10个数怎么办?










那我们就可以在不同的地方在一些k标点。
也就是K个很大的数,确保他们是最大的前K个。
然后只需要看结果是不是这k个数即可。

大家发现结果就是我们手动给的这10个数。说明我们的程序时没问题的。
后言
这就是建堆算法复杂度分析及TOP-K问题。这里涉及到许多数学知识。大家可以多看几遍证明图。今天就分享到这里。感谢大佬们垂阅!咱们下期见!拜拜~

相关文章:

【数据结构】建堆算法复杂度分析及TOP-K问题
【数据结构】建堆算法复杂度分析及TOP-K问题 🔥个人主页:大白的编程日记 🔥专栏:数据结构 文章目录 【数据结构】建堆算法复杂度分析及TOP-K问题前言一.复杂度分析1.1向下建堆复杂度1.2向上建堆复杂度1.3堆排序复杂度 二.TOP-K问…...

Thinkphp5实现前后端通过接口通讯基本操作方法
在ThinkPHP5框架中,实现前后端通过接口通讯是一个常见的需求,尤其是在开发RESTful API时。下面是一个基本的步骤指南,用于设置ThinkPHP5来创建API接口,并使前端能够通过HTTP请求与后端进行通讯。 1. 创建API模块 首先࿰…...

Go 语言任务编排 WaitGroup
WaitGroup 是常用的 Go 同步原语之一,用来做任务编排。它要解决的就是并发-等待的问题: 现在有一个 goroutine A 在检查点 ( checkpoint ) 等待一组 goroutine 全部完成它们的任务,如果这些 goroutine 还没全部完成任务,那么 goroutine A 就会被阻塞在检查点,直到所有的 …...

星环科技推出知识库产品 AI PC时代数据交互方式变革
随着企业业务的快速发展,数据量呈爆炸式增长,有效的知识管理成为企业面临的重要问题。企业遇到的普遍问题是大量的结构化、半结构化数据存储在不同的系统中,需要用多种计算机语言进行检索。而大模型彻底改变了人们和数据的交互方式࿰…...

10道JVM经典面试题
1、 JVM中,new出来的对象是在哪个区? 2、 说说类加载有哪些步骤? 3、 JMM是什么? 4、 说说JVM内存结构? 5、 MinorGC和FullGC有什么区别? 6、 什么是STW? 7、 什么情况下会发生堆/栈溢出?…...

Redisson常用的数据结构及应用场景
Redisson 提供了一系列高级数据结构,这些数据结构封装了 Redis 的原生数据类型,提供了 Java API 的便利性和分布式特性。以下是 Redisson 中一些常用的数据结构,场景还在不断完善中: RBucket:这是一个简单的键值对存储…...

【实现100个unity特效之8】使用ShaderGraph实现2d贴图中指定部分局部发光效果
最终效果 寒冰法师 火焰法师 文章目录 最终效果寒冰法师火焰法师 素材一、功能分析实现方法基本思路Unity的Bloom后处理为什么关键部位白色?最终结果 二、 新建URP项目三、合并图片四、使用PS制作黑白图片方法一 手动涂鸦方法二 魔棒工具1. 拖入图片进PS࿰…...
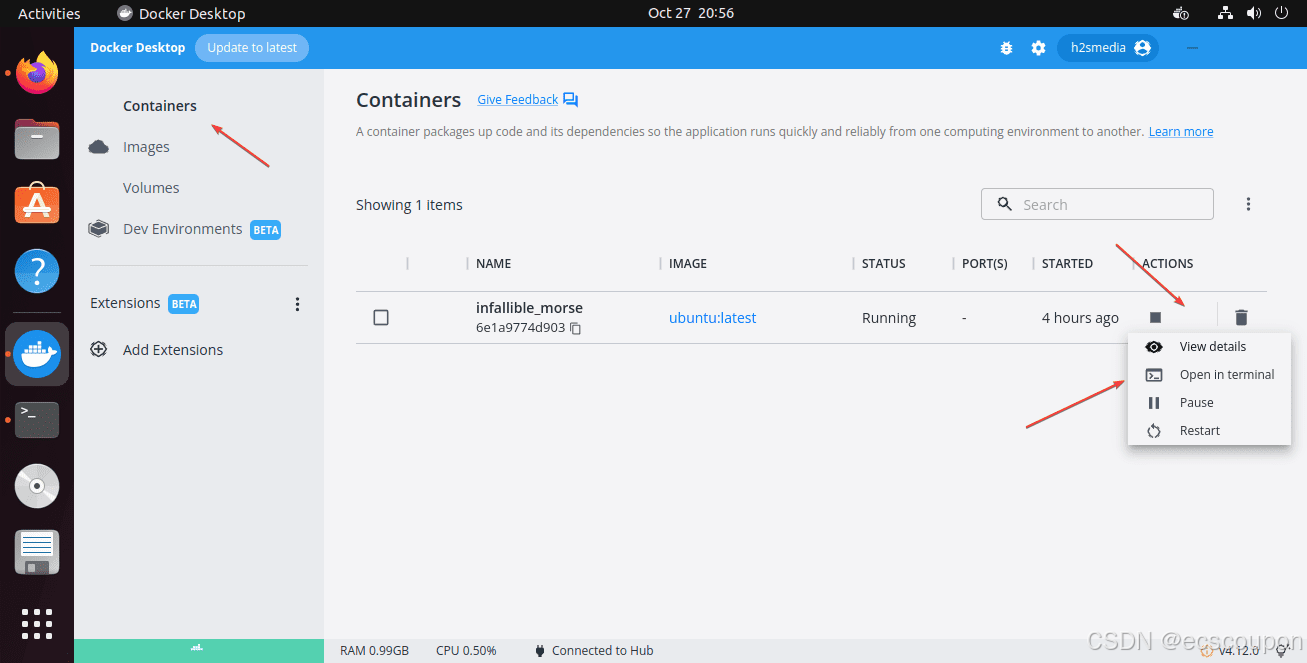
Ubuntu 24.04 LTS Noble安装Docker Desktop简单教程
Docker 为用户提供了在 Ubuntu Linux 上快速创建虚拟容器的能力。但是,那些不想使用命令行管理容器的人可以在 Ubuntu 24.04 LTS 上安装 Docker Desktop GUI,本教程将提供用于设置 Docker 图形用户界面的命令…… Docker Desktop 是一个易于使用的集成容…...

XML 和 SimpleXML 入门教程
XML 和 SimpleXML 入门教程 XML(可扩展标记语言)是一种用于存储和传输数据的标记语言。它是一种自我描述的语言,允许用户定义自己的标签来表示数据。SimpleXML 是 PHP 中的一个扩展,用于解析和操作 XML 数据。本文将介绍 XML 和 …...

leetcode--链表类题目总结
本文作为刷题时对链表类题目的总结. 常见技巧: 引入虚拟头节点 便于处理边界情况便于对链表操作快慢双指针(判环,找环的入口等)链表逆序(推荐使用 虚拟头节点 头插法 进行逆序) 链表逆序( 头插法 虚拟头节点):链表内指定区间反转_牛客题霸_牛客网 虚拟节点:合并…...

打卡第22天------回溯算法
开始学习了,希望我可以尽快成功上岸! 一、回溯理论基础 什么是回溯法?回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯是递归的副产品,只要有递归就会有回溯。 回溯法的效率回溯法的本质是穷举,穷举所有可能,然后找出我们想要的答案。如果想让回溯法高效一些,可…...

Ubuntu对比两个文件内容有什么区别?
在Ubuntu(或任何基于Linux的系统)中,你可以使用多种命令行工具来比较两个文件的内容差异。以下是一些常用的方法: 1. **diff 命令**: diff 是Linux中用于比较两个文件差异的标准工具。它逐行比较文件,并显示…...

python:本机摄像头目标检测实时推理(使用YOLOv8n模型)
本文将介绍如何使用本机摄像头进行目标检测实时推理的python代码。 文章目录 一、下载YOLO权重文件二、环境配置三、完整代码 一、下载YOLO权重文件 https://github.com/ultralytics/ultralytics?tabreadme-ov-file 拉到网页最下面,选择适合的模型,下…...

Spark实时(四):Strctured Streaming简单应用
文章目录 Strctured Streaming简单应用 一、Output Modes输出模式 二、Streaming Table API 三、Triggers 1、unspecified(默认模式) 2、Fixed interval micro-batches&am…...

SpringBoot上传超大文件导致OOM,完美问题解决办法
问题描述 报错: Caused by: java.lang.OutOfMemoryError at java.io.ByteArrayOutputStream.hugeCapacity(ByteArrayOutputStream.java:123) ~[?:1.8.0_381] at java.io.ByteArrayOutputStream.grow(ByteArrayOutputStream.java:117) ~[?:1.8.0_381] at java.…...

PyTorch 的各个核心模块和它们的功能
1. torch 核心功能 张量操作:PyTorch 的张量是一个多维数组,类似于 NumPy 的 ndarray,但支持 GPU 加速。数学运算:提供了各种数学运算,包括线性代数操作、随机数生成等。自动微分:torch.autograd 模块用于…...

Java开发之LinkedList源码分析
#来自ゾフィー(佐菲) 1 简介 LinkedList 的底层数据结构是双向链表。可以当作链表、栈、队列、双端队列来使用。有以下特点: 在插入或删除数据时,性能好;允许有 null 值;查询效率不高;线程不安…...

外卖霸王餐系统架构怎么选?
在当今日益繁荣的外卖市场中,外卖霸王餐作为一种独特的营销策略,受到了众多商家的青睐。然而,要想成功实施外卖霸王餐活动,一个安全、稳定且高效的架构选择至关重要。本文将深入探讨外卖霸王餐架构的选择,以期为商家提…...

AV1技术学习:Transform Coding
对预测残差进行变换编码,去除潜在的空间相关性。VP9 采用统一的变换块大小设计,编码块中的所有的块共享相同的变换大小。VP9 支持 4 4、8 8、16 16、32 32 四种正方形变换大小。根据预测模式选择由一维离散余弦变换 (DCT) 和非对称离散正弦变换 (ADS…...

Git操作指令
Git操作指令 一、安装git 1、设置配置信息: # global全局配置 git config --global user.name "Your username" git config --global user.email "Your email"2、查看git版本号 git -v # or git --version3、查看配置信息: git…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

