高完整性系统工程(三): Logic Intro Formal Specification
目录
1. Propositions 命题
2.1 Propositional Connectives 命题连接词
2.2 Variables 变量
2.3 Sets
2.3.1 Set Operations
2.4 Predicates
2.5 Quantification 量化
2.6 Relations
2.6.1 What Is A Relation?
2.6.2 Relations as Sets
2.6.3 Binary Relations as Pictures
2.6.4 Relation Example
2.6.5 Functions
2.6.6 Total vs Partial Functions 全函数 VS 部分函数
2.6.7 Relation Operations
2.6.8 Relation Joins
3. TEMPORAL LOGIC 时序逻辑
3.1 Next State
3.1.1 Transitions and Traces
3.2 Temporal Operators 时间运算符
4. SPECIFICATIONS SAY “WHAT” DESIGNS SAY “HOW”
4.1 Specifying Software
4.2 Aside: Functions as Relations
4.3 Modelling Data Types
4.4 Sequences as Relations 作为关系的序列
4.5 Searching
4.6 Pre and Postconditions 前置条件和后置条件
4.7 Formal Model-Based Specs
4.8 Advantages
4.9 Effect on Cost
4.10 Disadvantages
4.11 Difficulty
5. SPECIFICATIONS IN ALLOY
5.1 Alloy
6. LASTPASS DEMO
6.1 Alloy Modelling Overview
1. Propositions 命题
定义:A statement that is either true or false

2.1 Propositional Connectives 命题连接词

2.2 Variables 变量
Variables allow propositions to talk about state

Variables talk about different parts of the state of the formal model. (not state of the system/program)
2.3 Sets
A collection of things


2.3.1 Set Operations
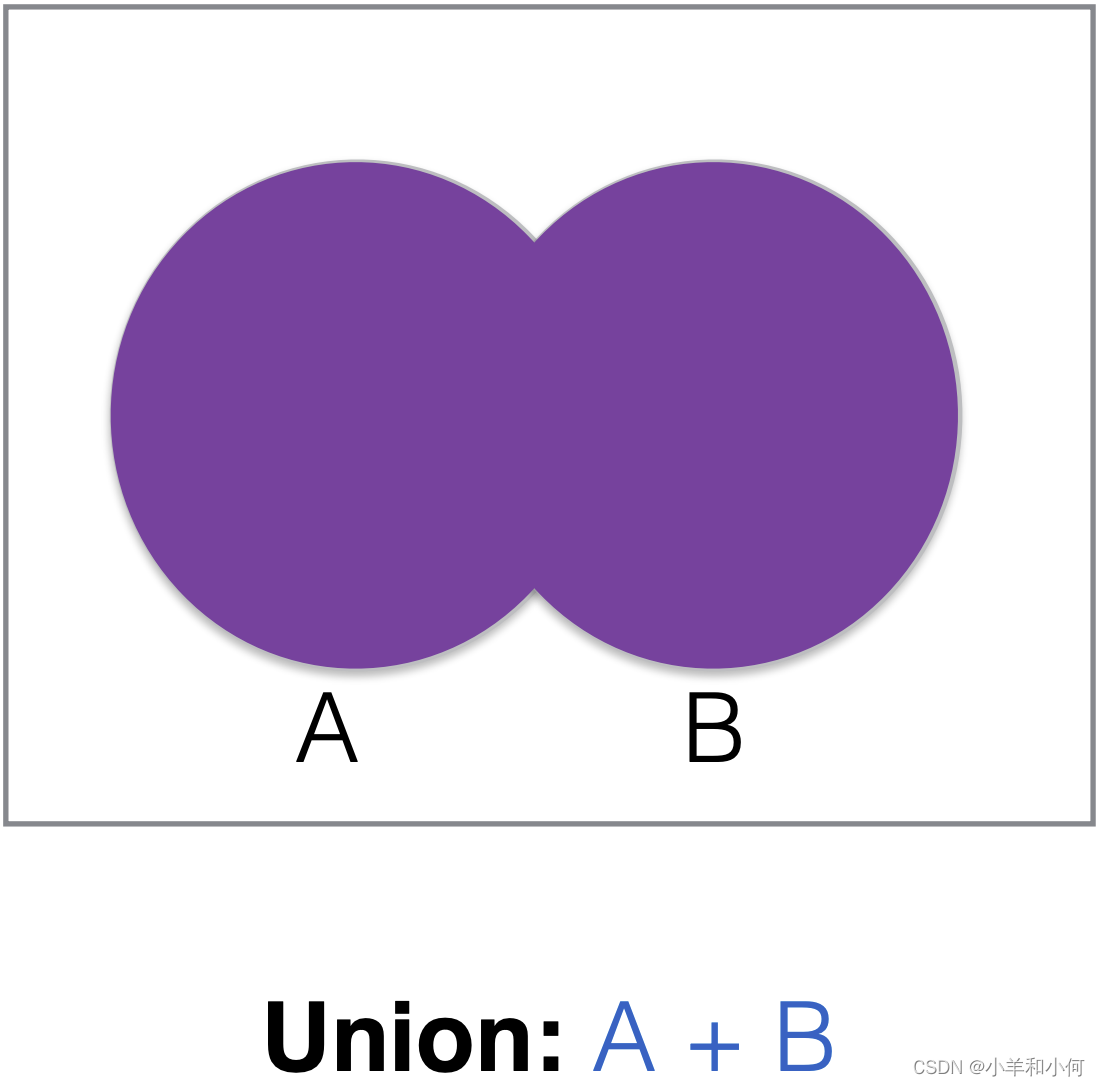
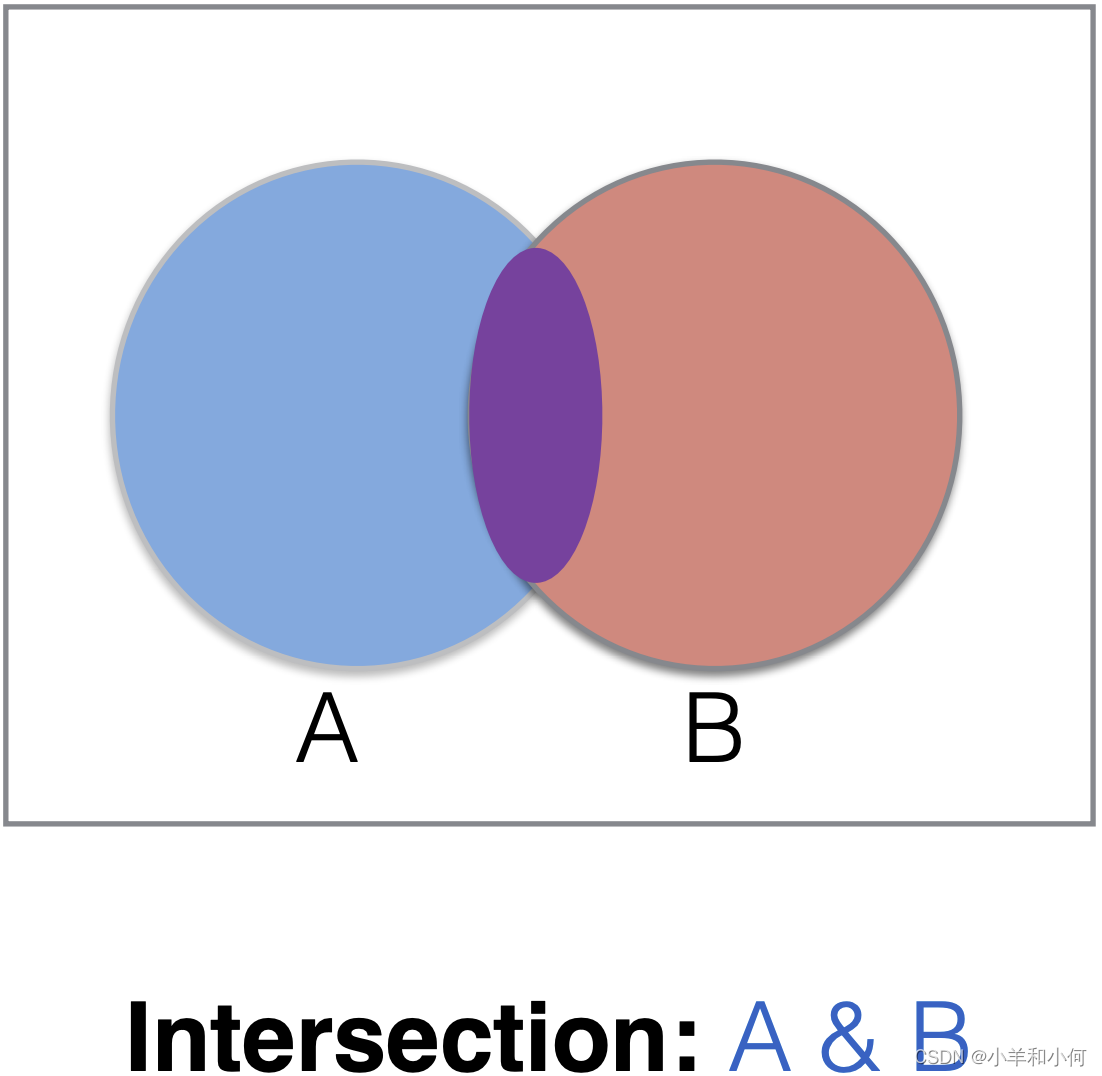
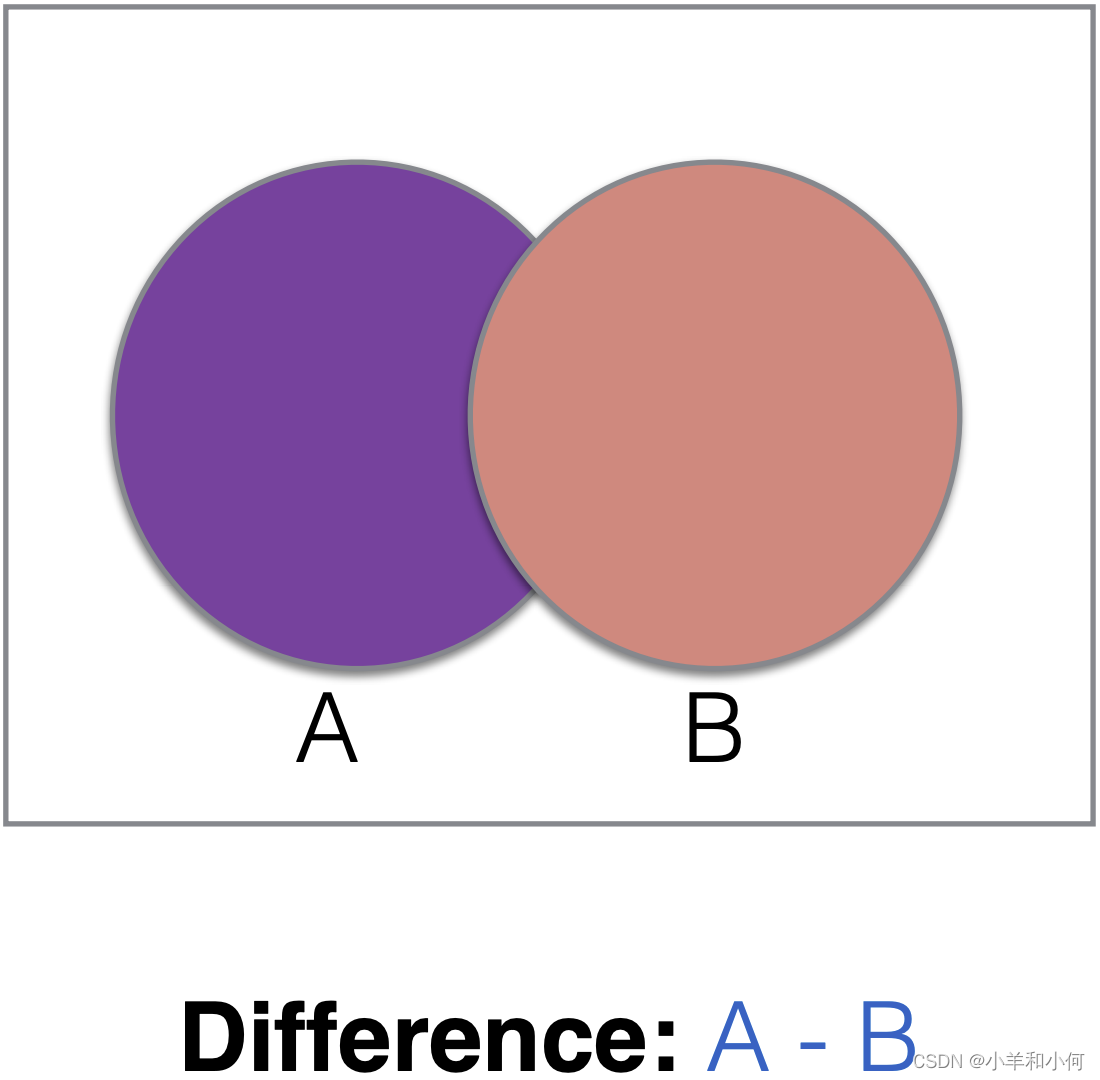

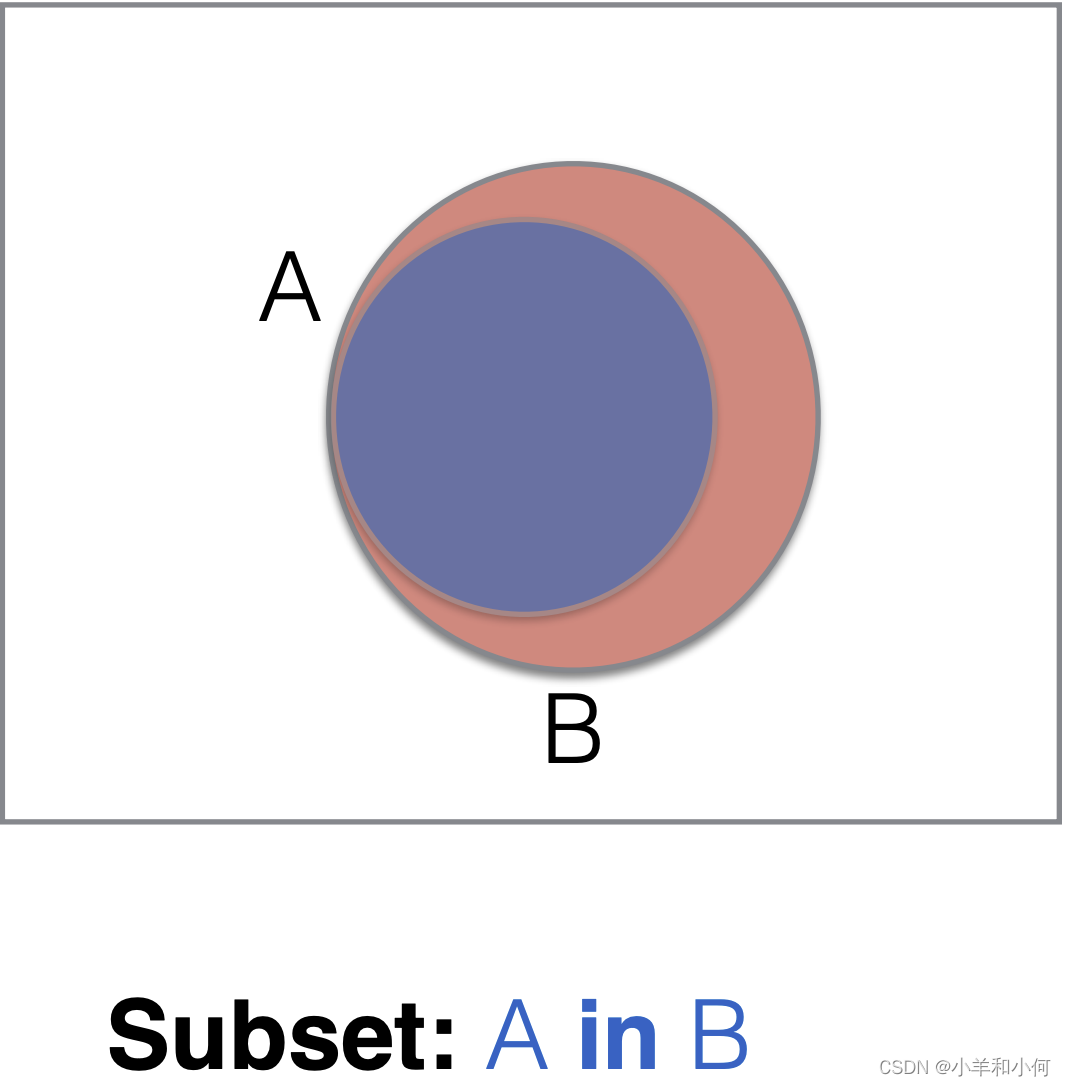
2.4 Predicates
Extend propositions with the ability to quantify the values of a variable that a proposition is true for
all: Proposition P(x) holds for all values of x
all x | P[x]
all city | Raining[city]
all city: AustralianCities | Raining[city]
some: Proposition P(x) holds for at least one value of x
some x | P[x]
some city | not Raining[city]
2.5 Quantification 量化
De Morgan’s Laws
all x | P[x] is equivalent to not some x | not P[x]
some x | P[x] is equivalent to not all x | not P[x]
Alloy Specific Quantifiers
one x | P[x] P(x) holds for exactly one value x
lone x | P[x] P(x) holds for at most one value x
none x | P[x] P(x) holds for no value x
2.6 Relations
A proposition that relates things together =, <, etc.
arity: the number of things the relation relates =, < etc. are all binary relations; relate two numbers 3 < 4, (5 - 1) = (3 + 1), etc.
A relation that relates three things together: IsSum(x,y,z) <=> z = x + y
Relations are just predicate
2.6.1 What Is A Relation?
How would you write down unambiguously what a relation means?
Simplest answer: just list all of the things it relates together.

Any relation is a simply a set of tuples.
2.6.2 Relations as Sets
Factor(x,y,z) — {(x,y,z) | x = y * z}
{(1,1,1), (2,1,2), (2,2,1), (3,1,3), (3,3,1),(4,4,1), (4,2,2),…}
Use Factor to define when a number is prime, i.e. define the predicate IsPrime[x] 使用Factor来定义一个数字何时是质数,即定义谓词IsPrime[x]。
all y,z | (x,y,z) in Factor implies y = 1 or z = 1
A relation with arity n (i.e. an n-ary relation) R, is a set of n-tuples of atoms. 一个有n个算数的关系(即n-ary关系)R,是一个由n个原子图元组成的集合。
A binary (2-ary) relation R(a,b) is a set of: pairs
A ternary (3-ary) relation R(a,b,c) is a set of: triples
A unary (1-ary) relation R(a) is a set of: atoms
Sets are relations, and relations are sets. 集合是关系,而关系是集合。
Sets are predicates, and predicates are sets. 集合是谓词,而谓词是集合。
Relations are predicates, and predicates are relations. 关系是谓词,而谓词是关系。
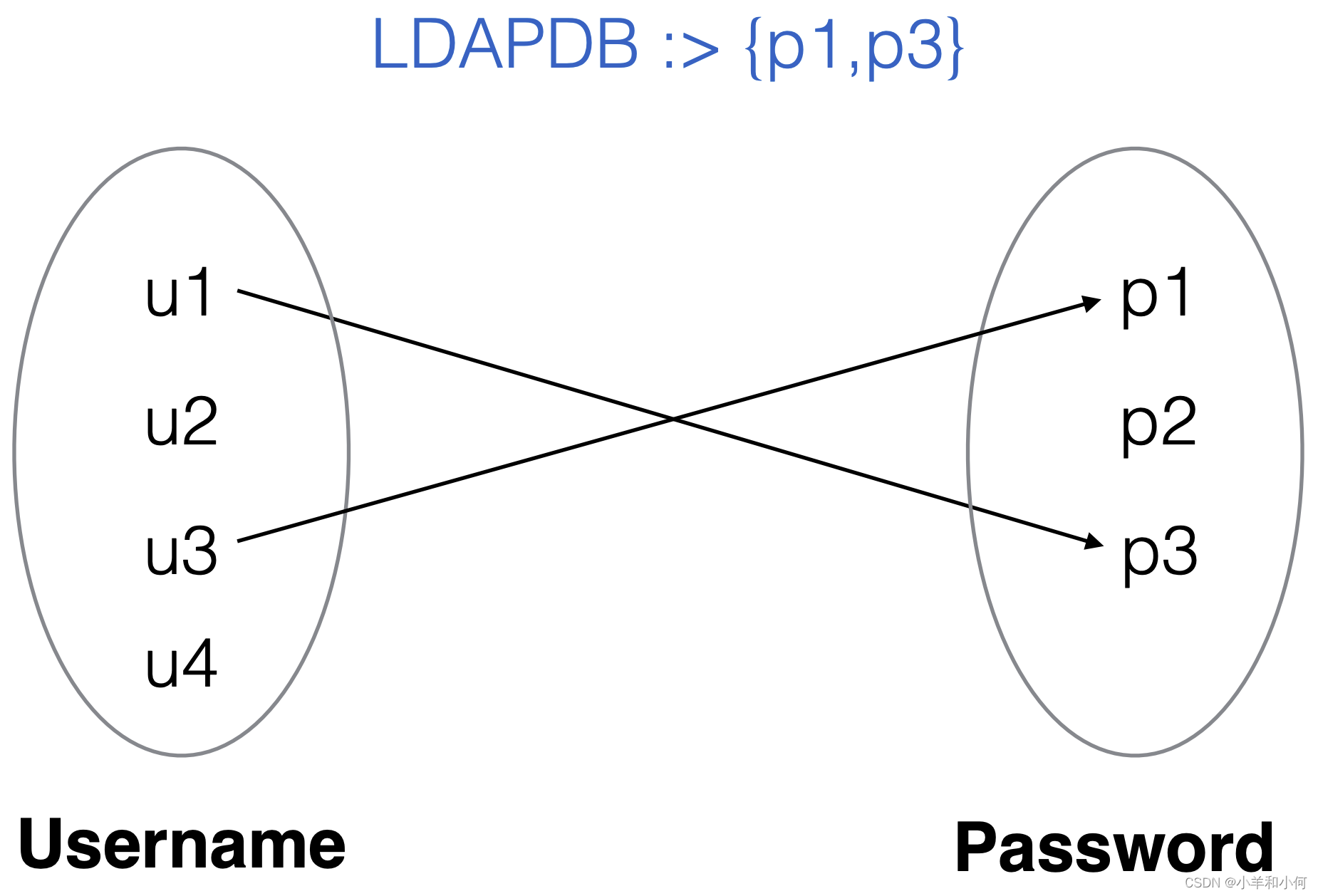
2.6.3 Binary Relations as Pictures
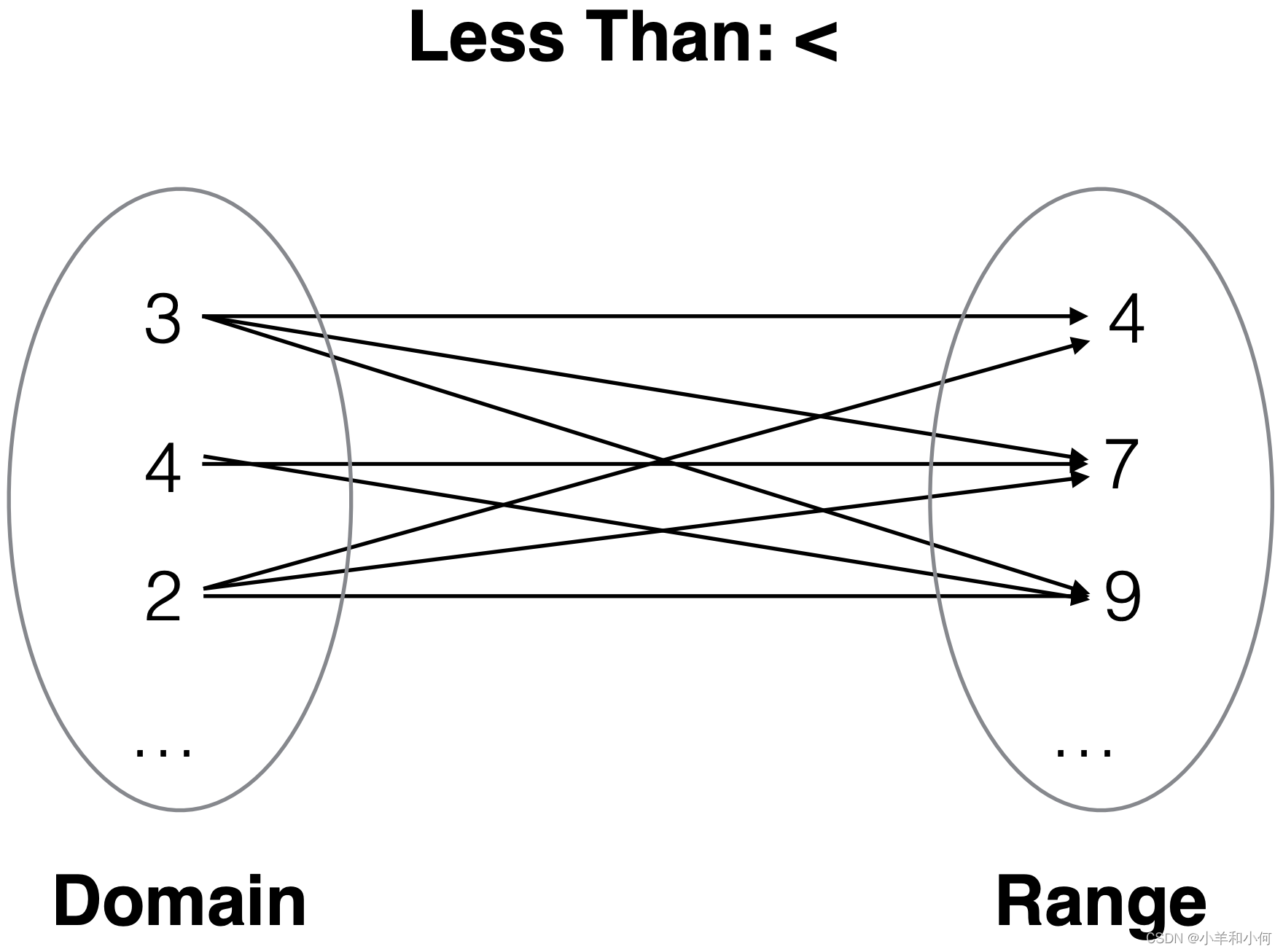
2.6.4 Relation Example
Imagine 2 sets of atoms:
Username = {n1, n2, …}
Password = {p1, p2, …}
Imagine an LDAP username/password database.
LDAPDB : Username -> Password
LDAPDB ⊆ 𝒫 (Username x Password)

2.6.5 Functions
For every username, there is only one password in LDAPDB
all u:Username, pw1:Password, pw2:Password | LDAPDB(u,pw1) and LDAPDB(u,pw2) implies pw1 = pw2

2.6.6 Total vs Partial Functions 全函数 VS 部分函数
LDAPDB : Username -> Password
Does every username in Username have a password?
A total function gives an answer for every (type-correct) argument
A partial function is one that is not total
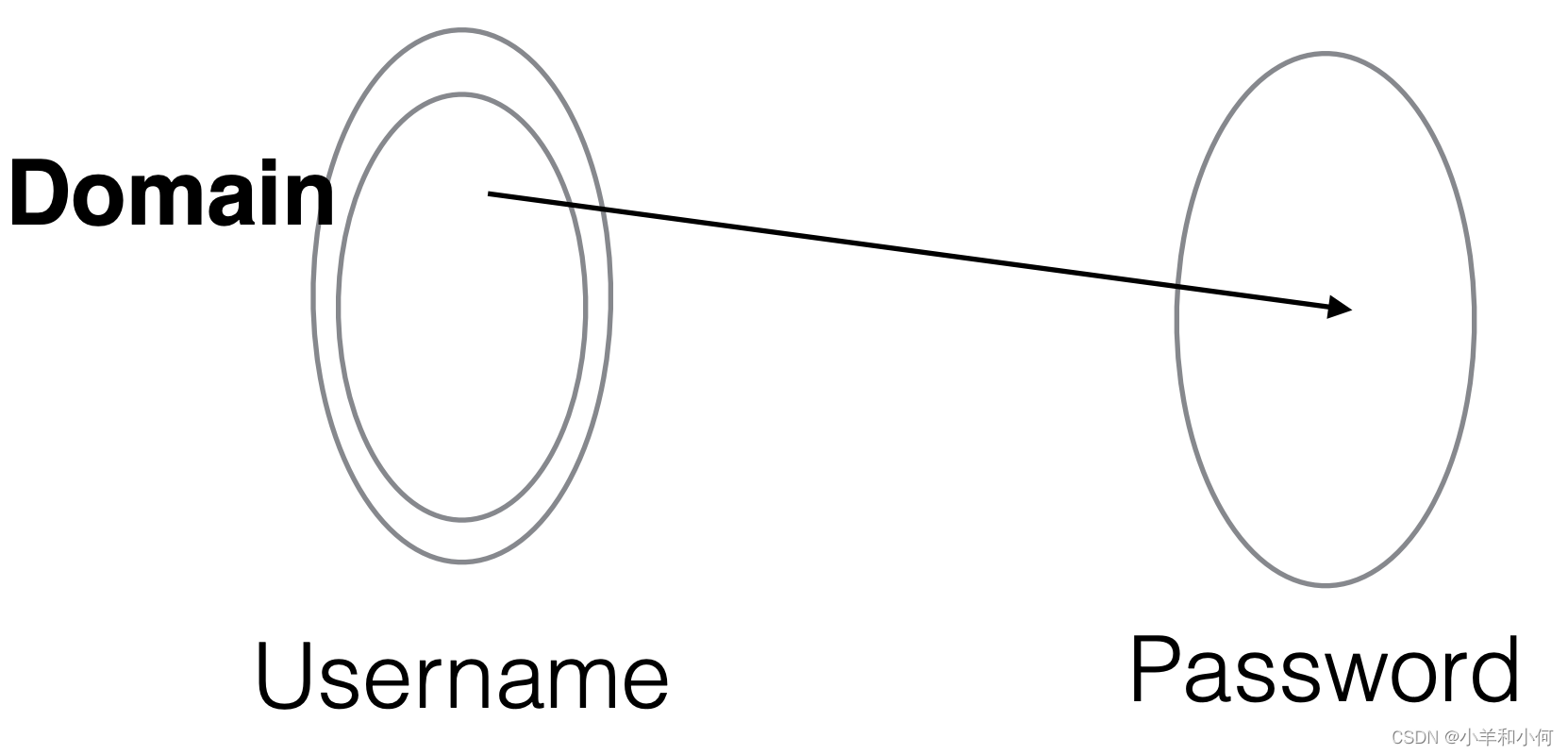
2.6.7 Relation Operations
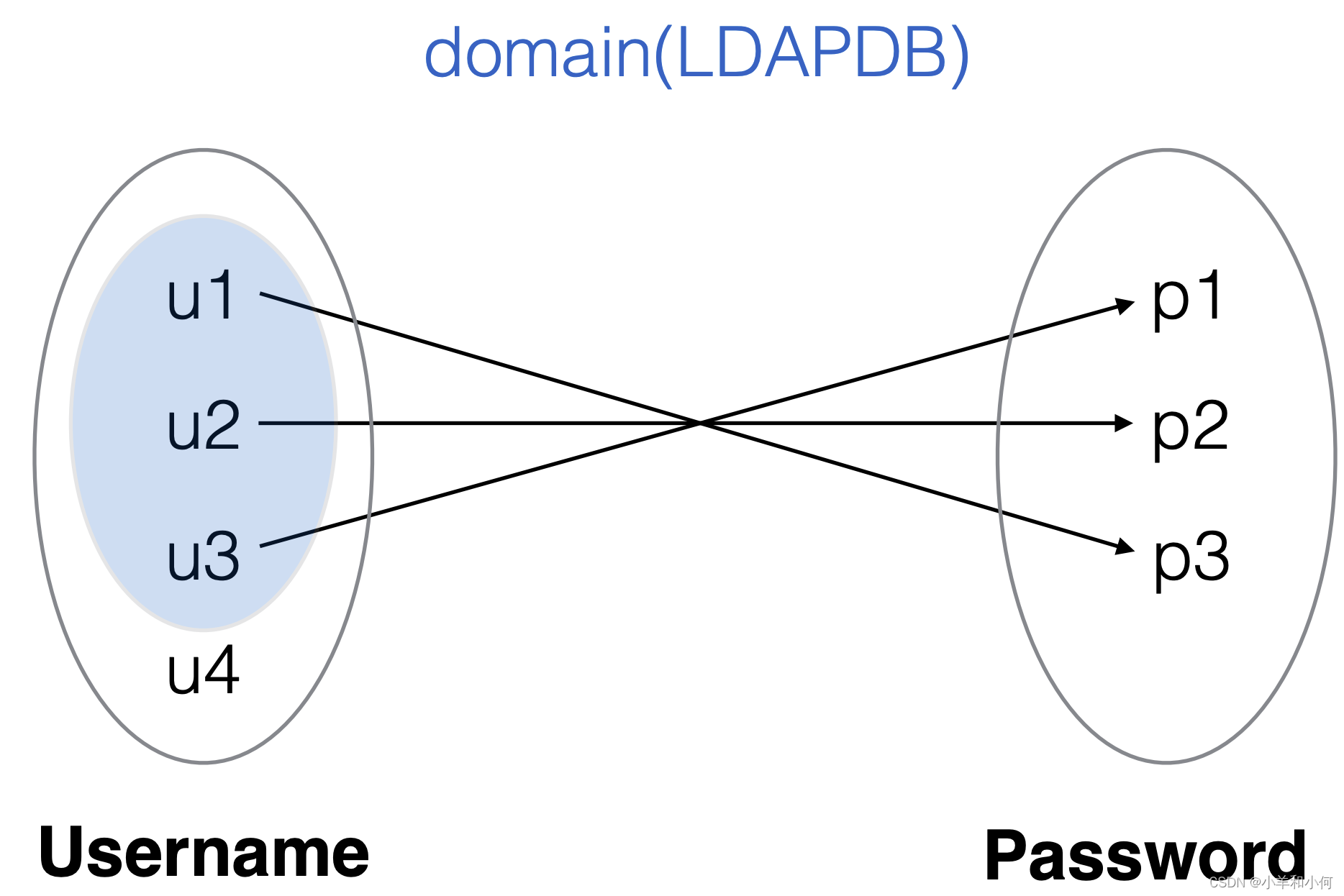
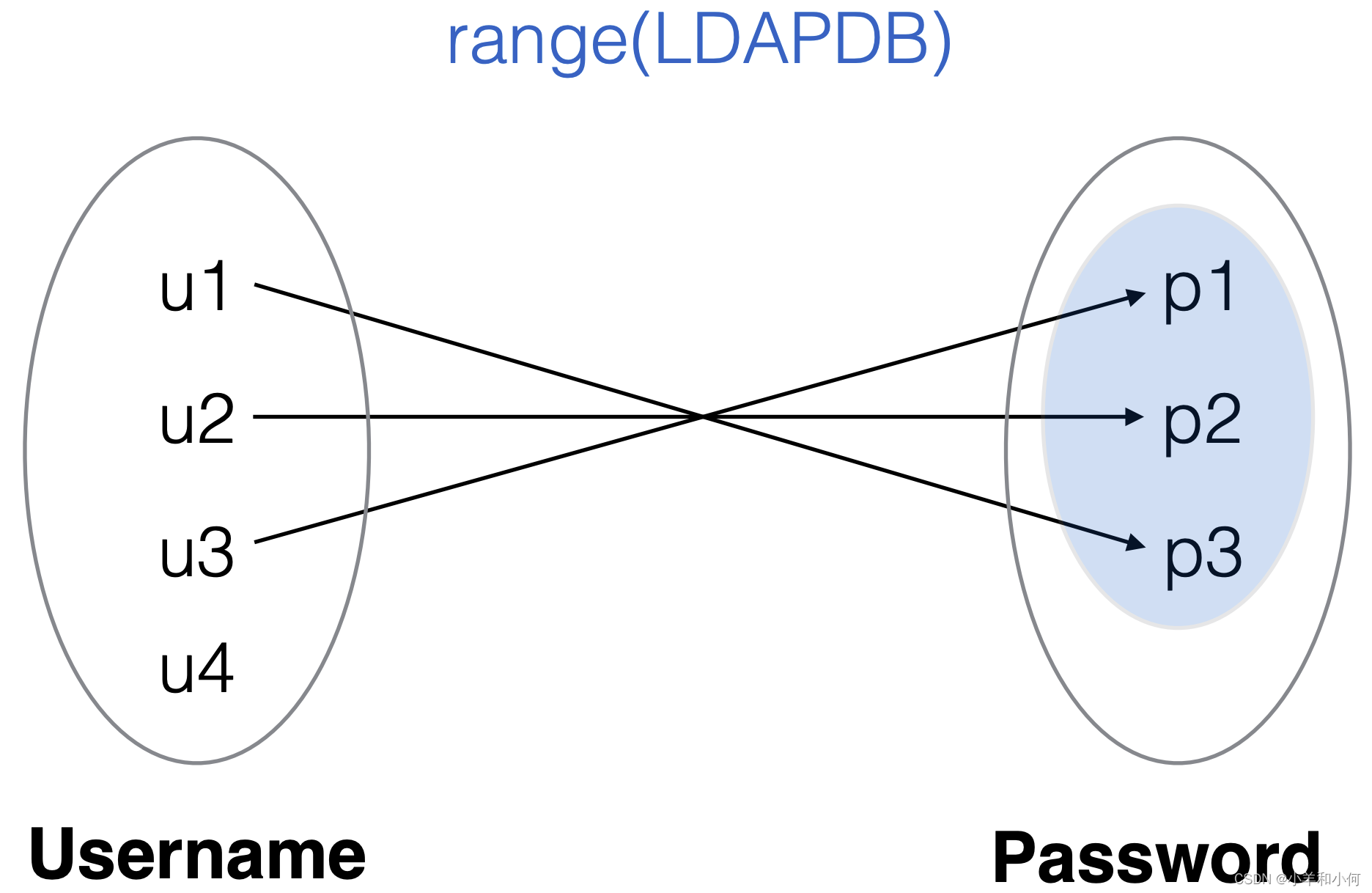
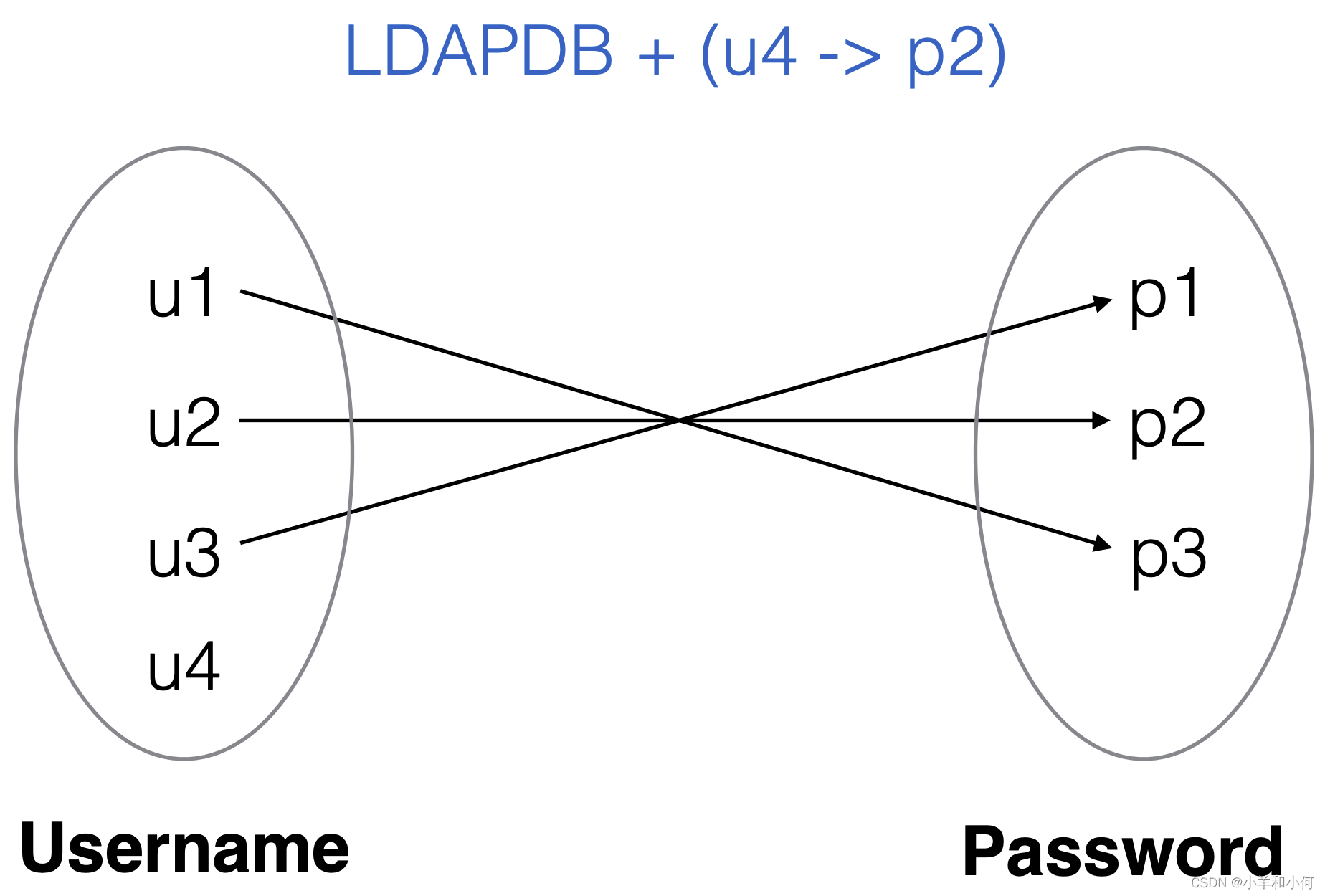
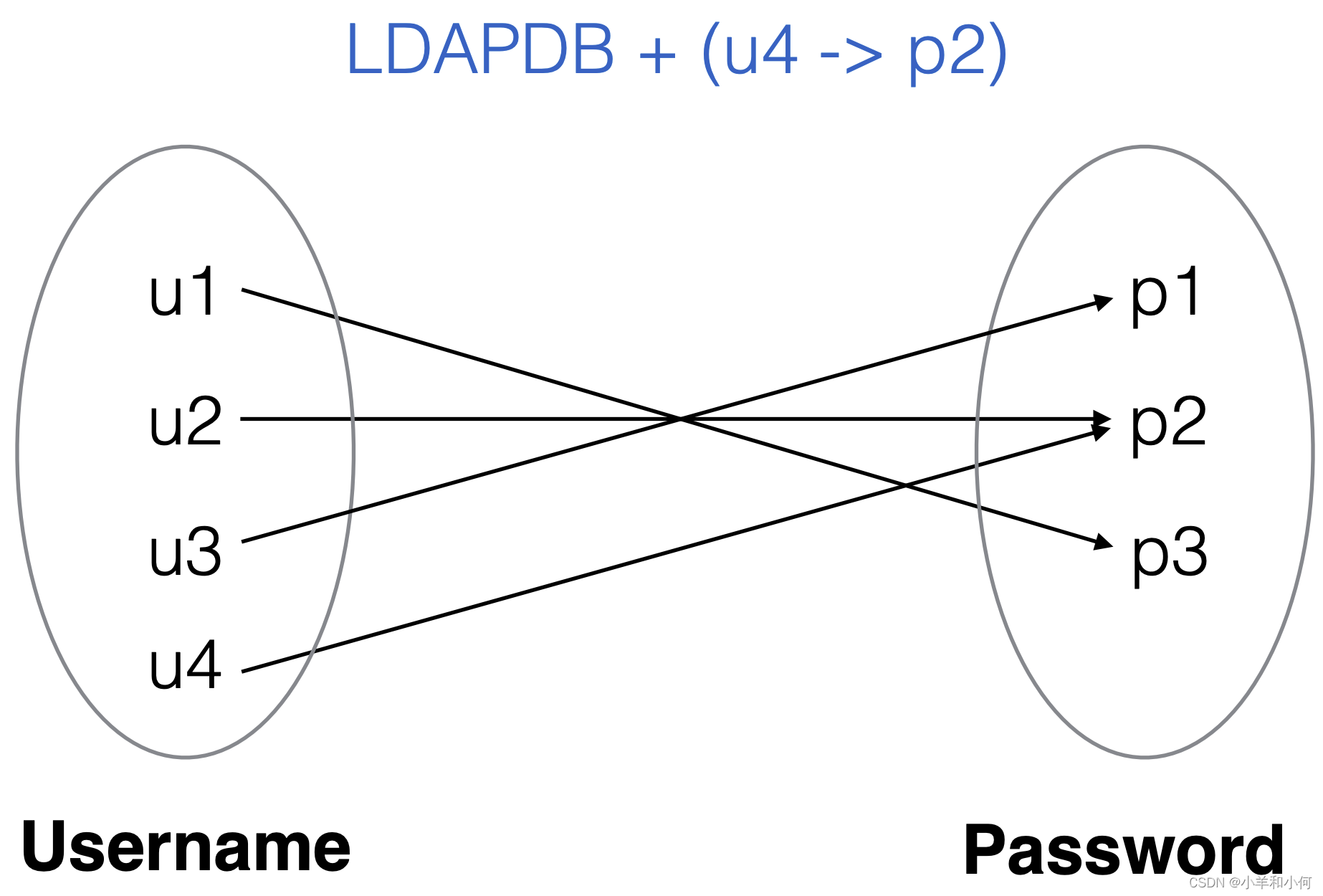
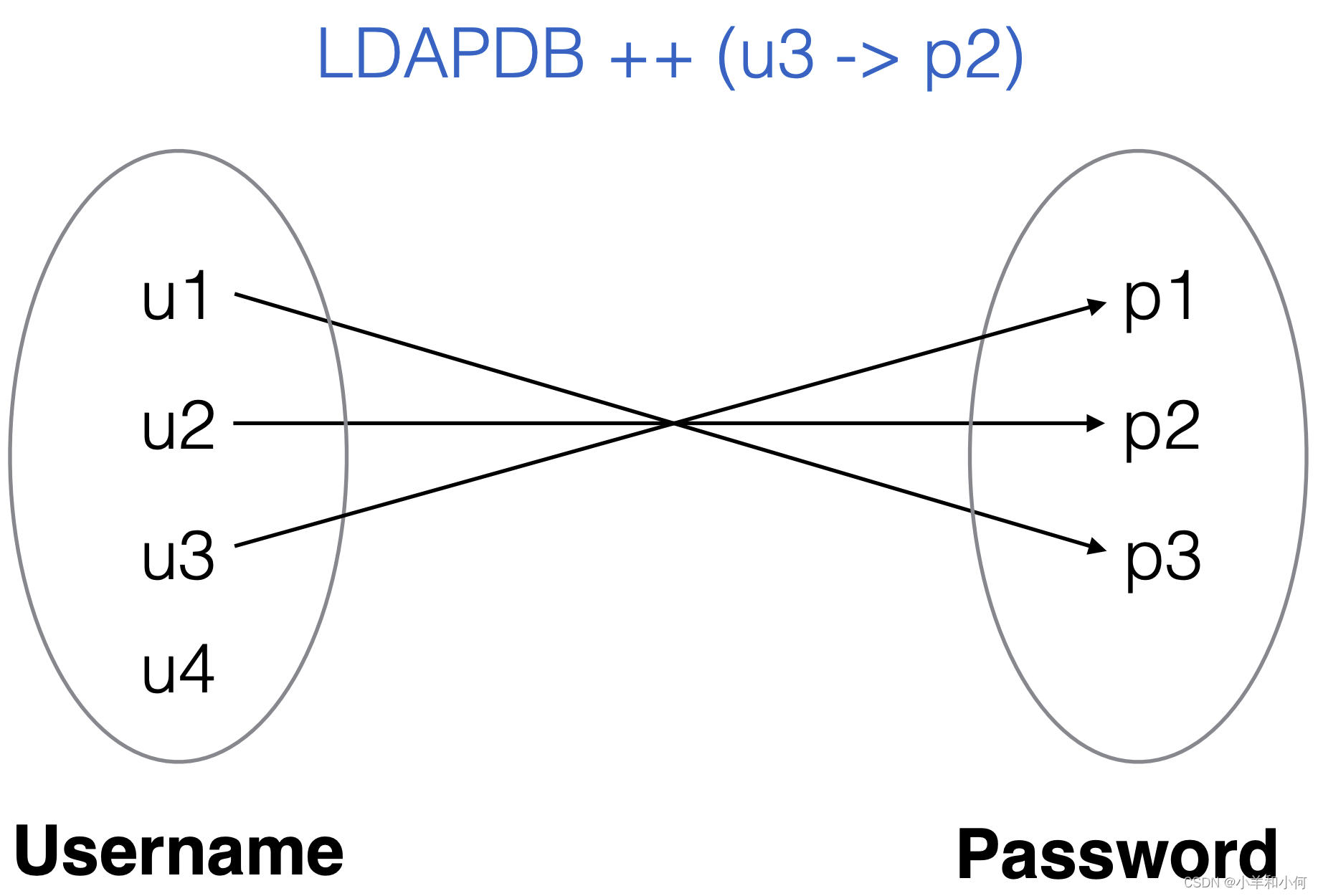 xQ
xQ
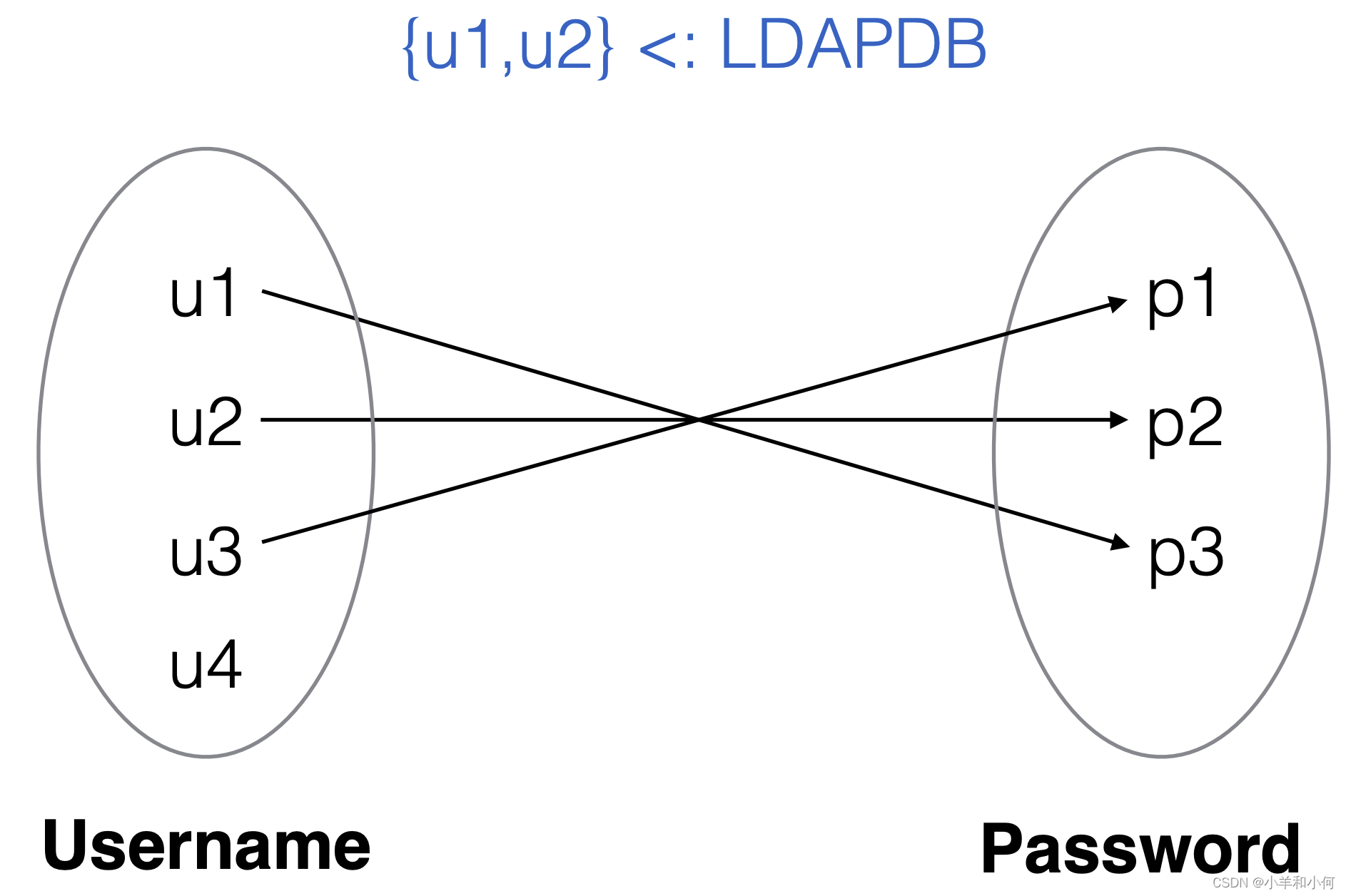


2.6.8 Relation Joins




3. TEMPORAL LOGIC 时序逻辑
3.1 Next State
if x is a variable, then x’ refers to x’s value in the next state 如果x是一个变量,那么x'指的是x在下一个状态中的值
To specify that x is incremented, we would write 要指定x被递增,我们可以写成
x’ = x + 1
Predicates that talk about x are also allowed to talk about x’s value in future states, e.g. x’, x’’ etc. and how it relates to x’s current value 谈论x的谓词也被允许谈论x在未来状态下的价值,例如x',x''等,以及它与x的当前价值的关系。
These predicates define state transitions 这些谓词定义了状态转换
3.1.1 Transitions and Traces

3.2 Temporal Operators 时间运算符
We can also write predicates that talk about future and even past states using temporal operators 我们还可以使用时间运算符编写谈论未来甚至是过去状态的谓词
always P
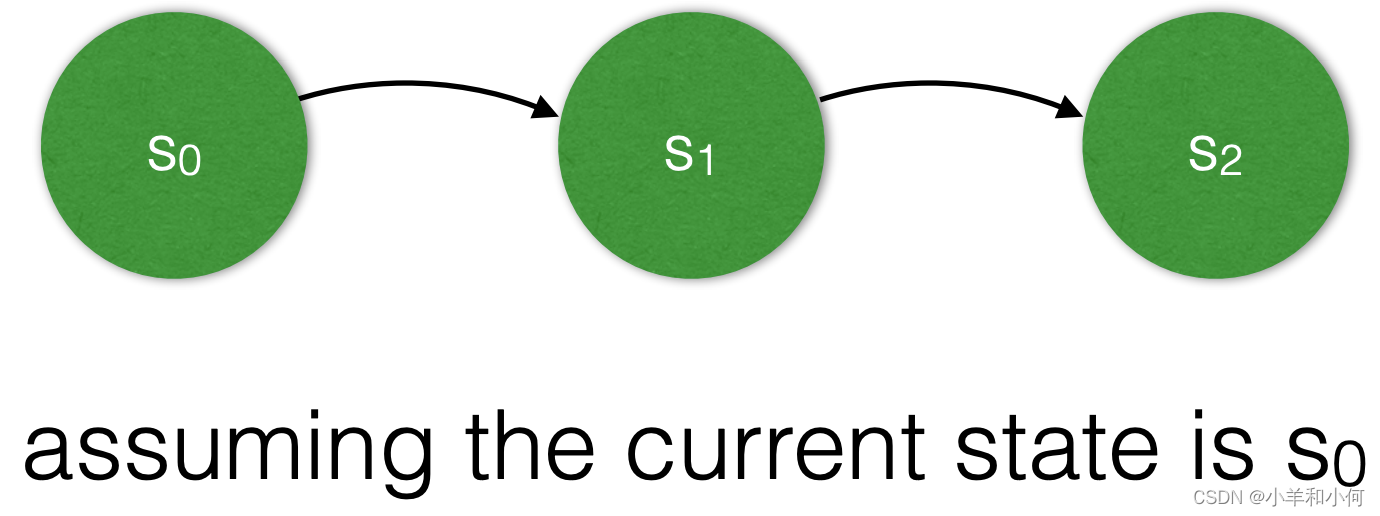
after P
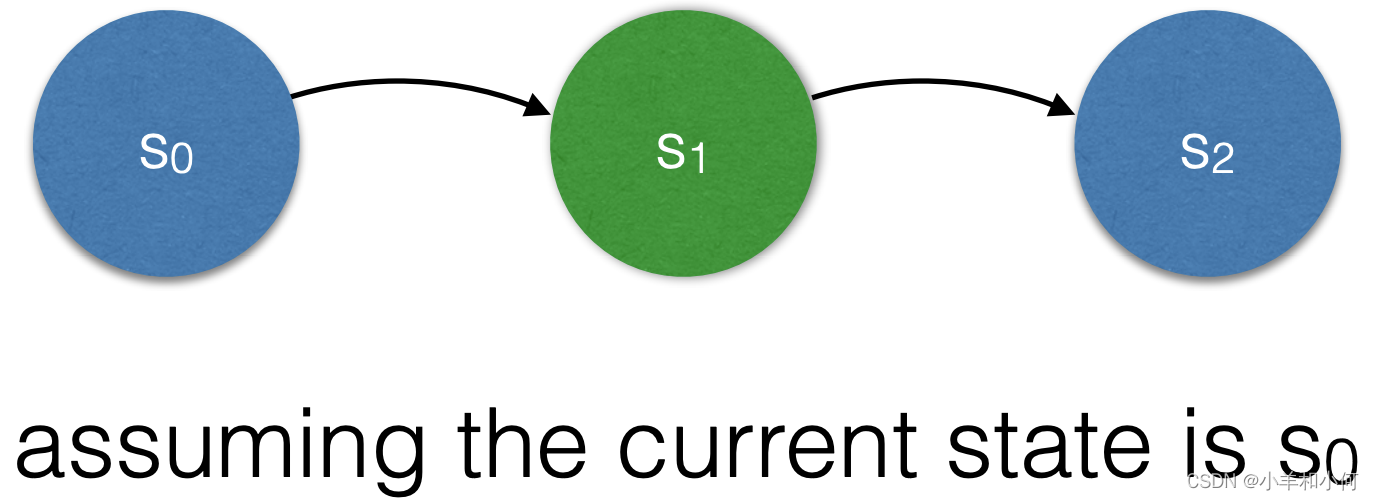
eventually P
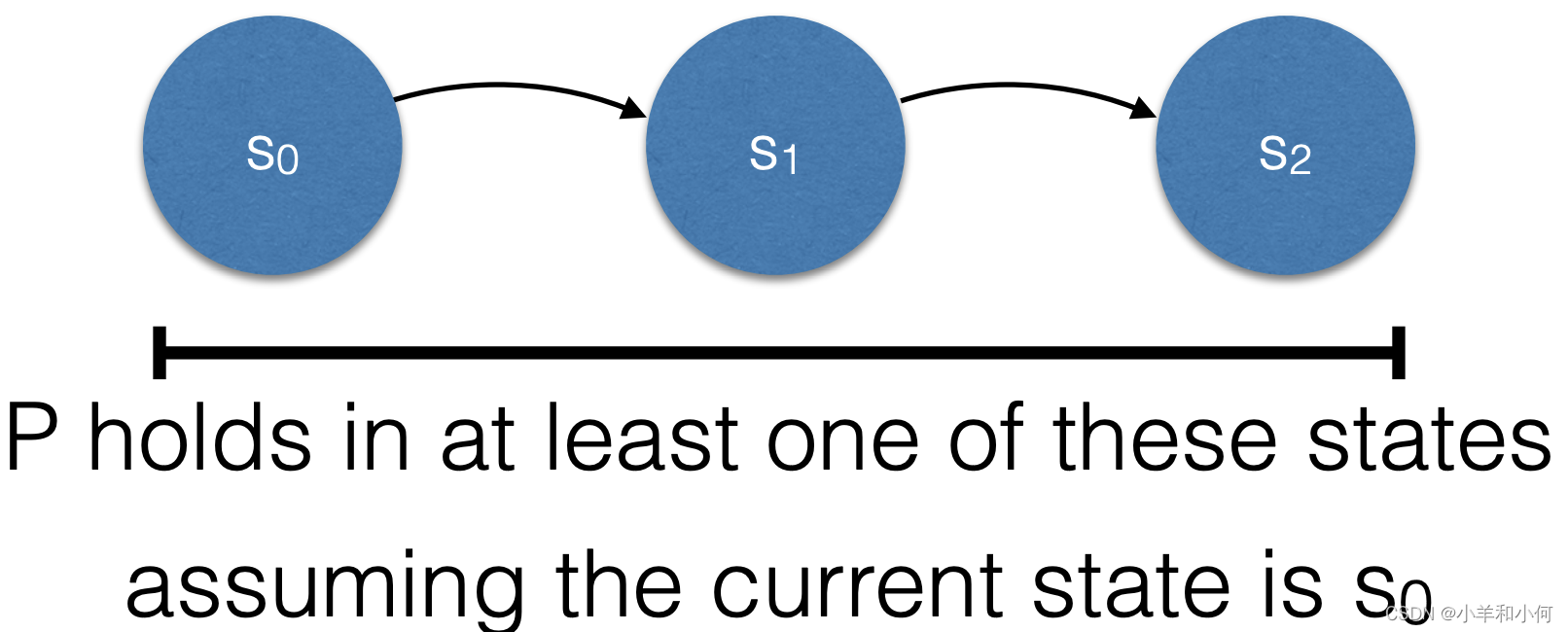
P; Q
equivalent to P and (after Q)
4. SPECIFICATIONS SAY “WHAT” DESIGNS SAY “HOW”
4.1 Specifying Software
Specify modules
Formally describe (an abstraction of) the module’s state 正式描述(抽象的)模块的状态
Formally describe the behaviour of the module’s operations (e.g. procedures, functions etc.). 正式描述模块的操作行为(如程序、函数等)
Behaviour specified in terms of state (transition) relations. 用状态(转换)关系来指定行为。
Trivial example: a counter
State: natural number n : ℕ
Operation: increment n’ = n+1
4.2 Aside: Functions as Relations

4.3 Modelling Data Types
Data types modelled as sets, relations, functions etc. 以集合、关系、函数等为模型的数据类型。

4.4 Sequences as Relations 作为关系的序列

4.5 Searching


4.6 Pre and Postconditions 前置条件和后置条件
Precondition: Specifies the assumptions made by a procedure/function 前提条件。指明一个程序/函数所做的假设
Postcondition: Specifies the behaviour, assuming that the precondition holds 后置条件。指定行为,假设前提条件成立
Precondition for binary search: list is sorted 二进制搜索的前提条件:列表被排序
sorted(list) <=> all i : ℤ | i < #list implies list[i] ≤ list[i+1]
4.7 Formal Model-Based Specs
Model the behaviour of each operation as a relation 将每个操作的行为建模为一种关系
The relation captures the relationship between the operation’s inputs and outputs 该关系捕捉到操作的输入和输出之间的关系
In general: relates the states before and after the operation 一般来说:将操作前后的状态联系起来
Says how they are allowed to differ (postcondition) under assumptions about the inputs (precondition) 说出了在关于输入(前提条件)的假设下允许它们有什么不同(后置条件)
Says what the operation does, not how it does it. 说的是操作做什么,而不是它如何做
4.8 Advantages
- Small
- Unambiguous
- Abstract from Implementation
- Machine-Checkable
- Forces thinking up-front
- Gets mistakes out of the way early (i.e. when they are cheaper to fix)
- 小型
- 毫不含糊
- 从实现中抽象出来
- 可由机器检查
- 迫使人们提前思考
- 尽早消除错误(即当它们的修复成本较低时)。
4.9 Effect on Cost
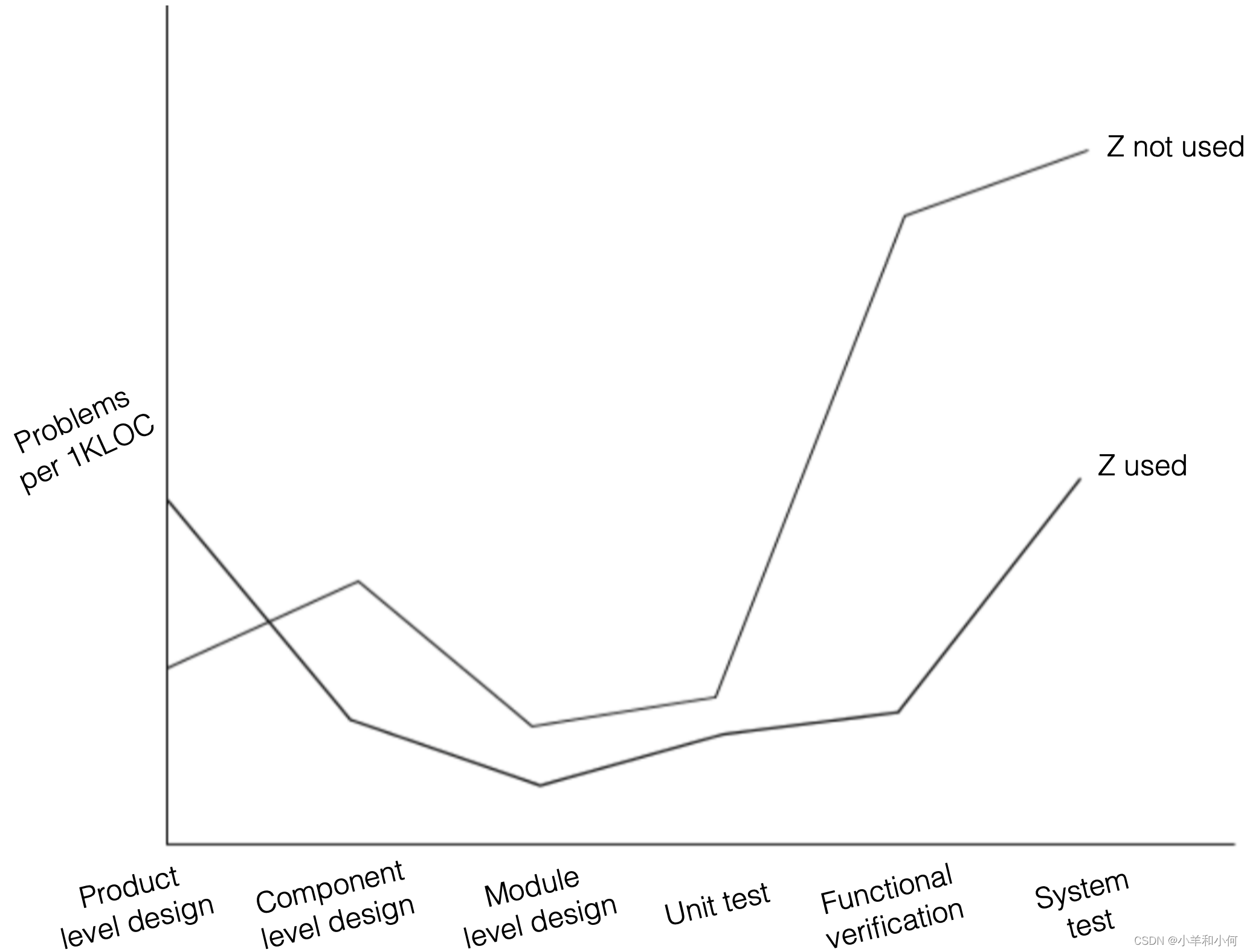
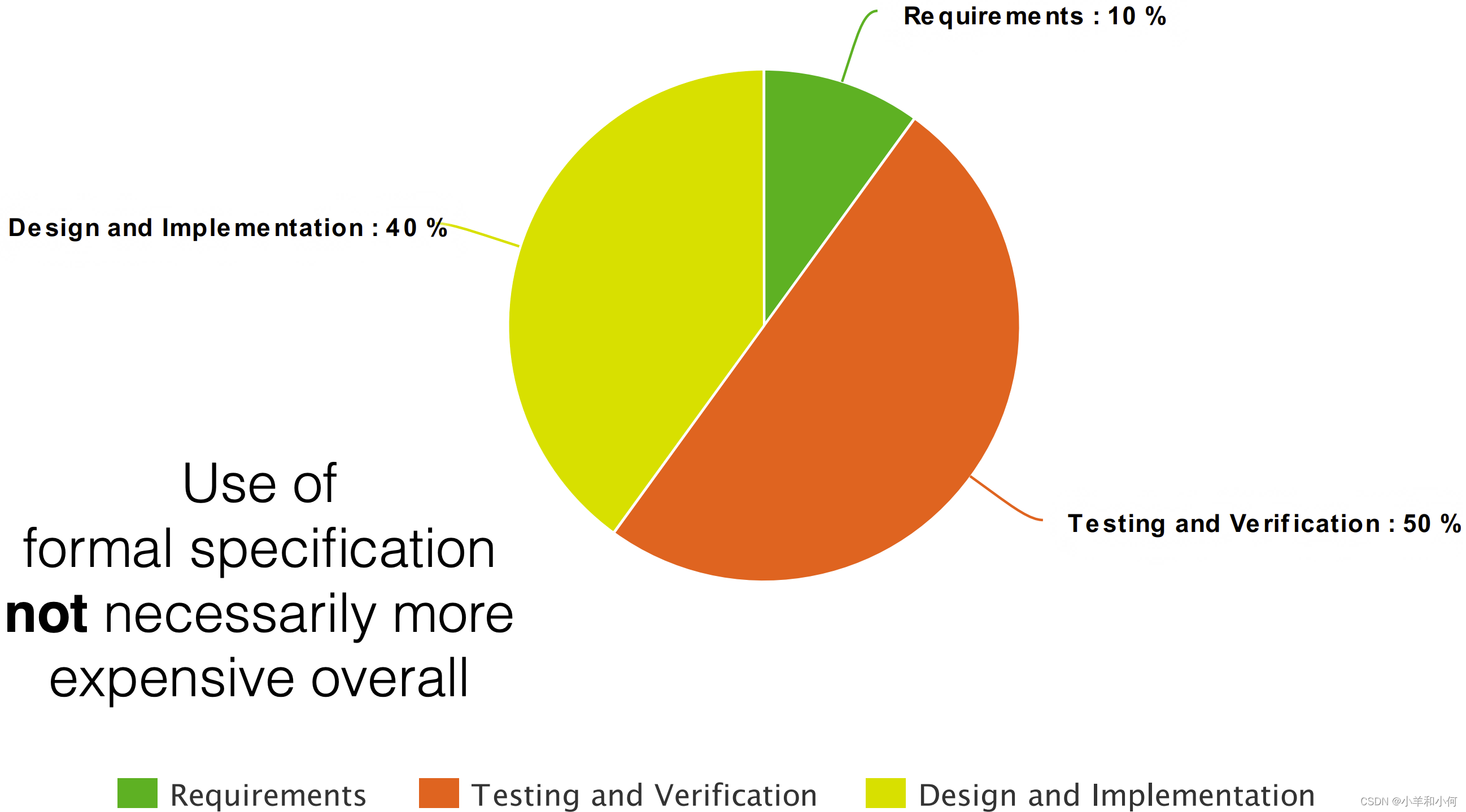
4.10 Disadvantages
- Requires specialised expertise 需要专门的专业知识
- Might lengthen time to implementation 可能会延长实施的时间
- Loads more effort early in the development process 在开发过程的早期要付出更多的努力
- Not necessarily well suited to projects with rapidly changing requirements. 不一定很适合于需求快速变化的项目
- (So it’s important to get your HAZOP etc. correct) (所以,正确地进行HAZOP等是很重要的)
4.11 Difficulty
All programmers know many formal languages 所有的程序员都知道许多形式语言
Specs are shorter and thus simpler to write than code 规范更短,因此比代码更容易编写
Specs say only what not how 规范只说什么,不说怎么做
Programs must say both 程序必须说明这两点
Ordinary programmers not trained to write and read formal specs 普通程序员没有受过编写和阅读正式规范的训练
5. SPECIFICATIONS IN ALLOY
5.1 Alloy
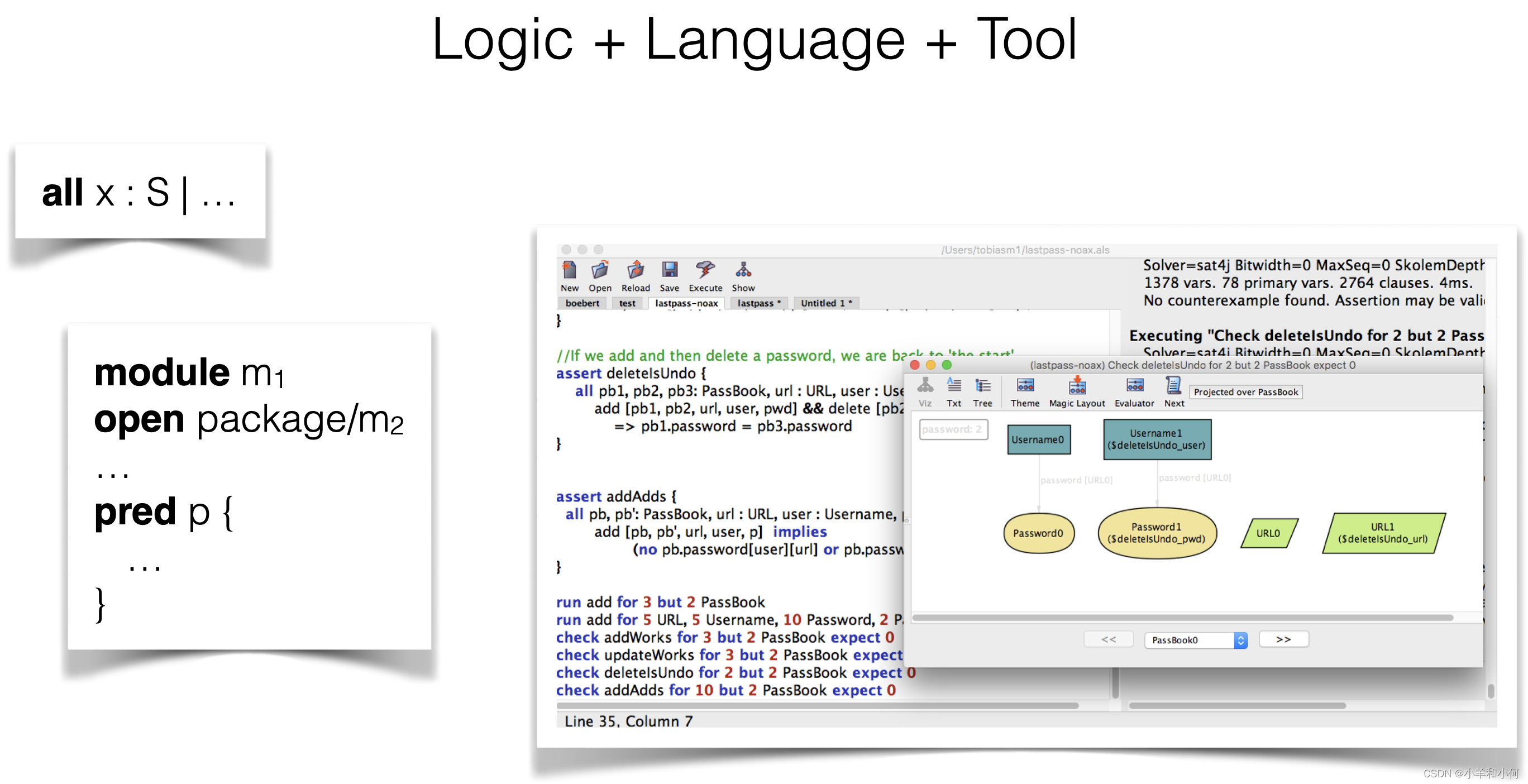
6. LASTPASS DEMO
6.1 Alloy Modelling Overview
signatures: declaring sets and relations 声明集合和关系
facts: axioms that hold over signatures and globally constrain the model to rule out nonsense 适用于签名的公理,并在全局上约束模型以排除无意义的东西
predicates: define relations between variables in a model, used to specify operations, state transitions 定义模型中变量之间的关系,用于指定操作和状态转换
functions: shorthand for expressions 表达式的简写
相关文章:

高完整性系统工程(三): Logic Intro Formal Specification
目录 1. Propositions 命题 2.1 Propositional Connectives 命题连接词 2.2 Variables 变量 2.3 Sets 2.3.1 Set Operations 2.4 Predicates 2.5 Quantification 量化 2.6 Relations 2.6.1 What Is A Relation? 2.6.2 Relations as Sets 2.6.3 Binary Relations as…...
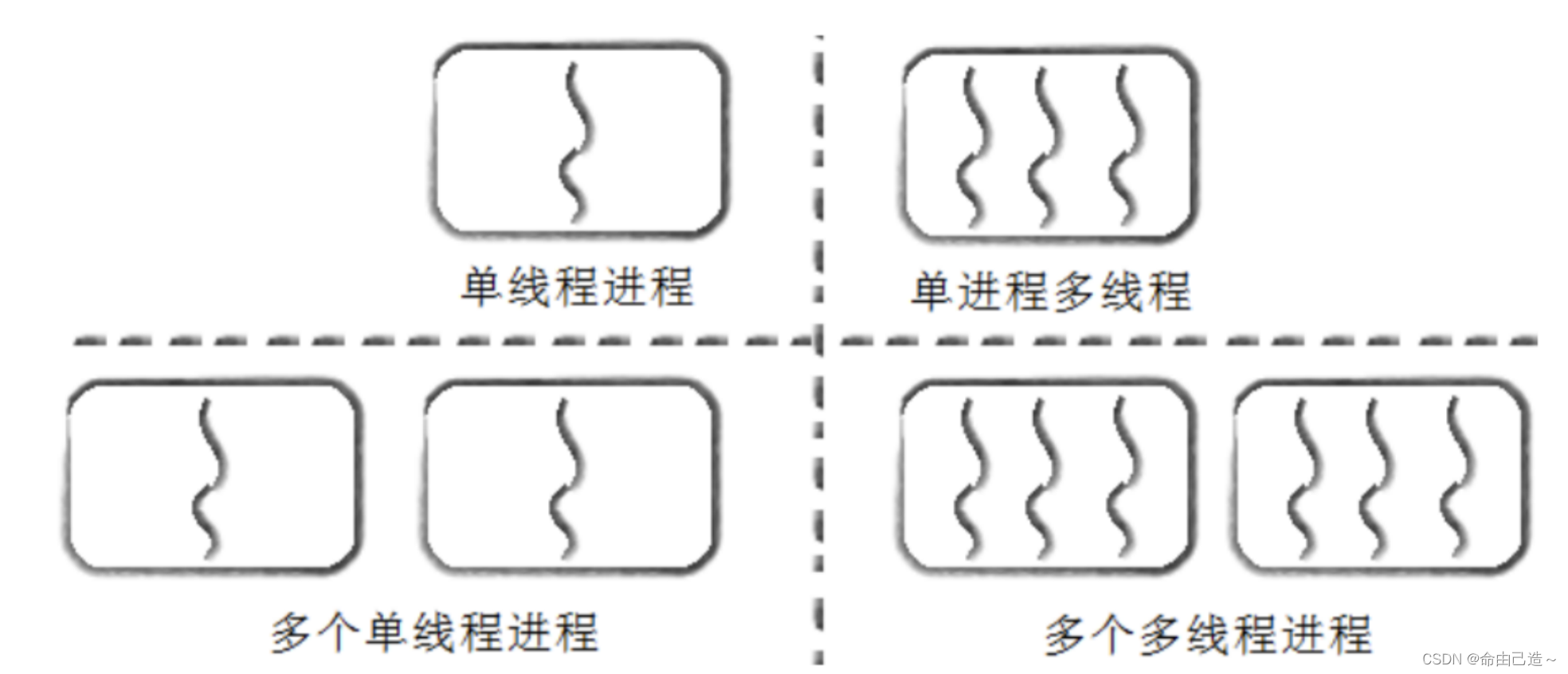
【linux】多线程概念详述
文章目录一、线程基本概念1.1 进程地址空间与页表1.2 页表结构1.3 线程的理解1.3.1 如何描述线程1.4 再谈进程1.5 代码理解1.5.1 原生库提供线程pthread_create1.6 资源共享问题1.7 资源私有问题二、总结2.1 什么是线程2.2 并行与并发2.3 线程的优点2.4 线程的缺点2.5 线程异常…...
方法 基本知识)
【Java】P8 面向对象(3)方法 基本知识
面向对象 方法方法方法的声明权限修饰符返回值类型方法名形参列表方法体简单案例方法 方法 是对类或对象行为特征的抽象,用来完成某个功能的操作。方法的目的 是为了实现代码复用,减少冗余,简化代码;方法不能独立存在,…...

js中null和undefined的区别
js中null和undefined的区别?这也是一个常见的js面试题 相同点 1,都是基本类型。 2,做判断值都是false。 !!null false // true !!undefined false // true不同点 1,诞生时间null在前,undefined在后。因为js作者Brendan-Eic…...
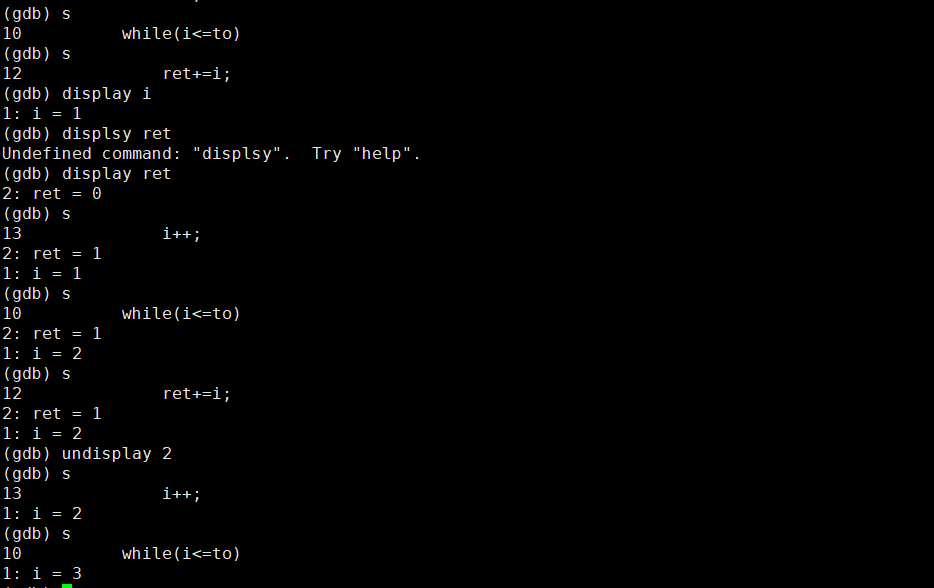
【Linux】linux中的c++怎么调试?gdb的介绍和使用。
背景1.1.前提知识程序的发布方式有两种,debug模式和release模式Linux gcc/g出来的二进制程序,默认是release模式 要使用gdb调试,必须在源代码生成二进制程序的时候, 加上 -g 选项windows上的调试方法有区别吗?1.调试思路是一样的2…...

提升Python代码性能的六个技巧
文章目录前言为什么要写本文?1、代码性能检测1.1、使用 timeit 库1.2、使用 memory_profiler 库1.3、使用 line_profiler 库2、使用内置函数和库3、使用内插字符串 f-string4、使用列表推导式5、使用 lru_cache 装饰器缓存数据6、针对循环结构的优化7、选择合适算法…...

VI的常用命令
VI的常用命令 文章目录VI的常用命令vi/vim是什么?VI普通模式命令VI编辑模式命令VI指令模式vi/vim是什么? VI是Unix操作系统和类Unix操作系统中最通用的文本编辑器 VIM编辑器是从VI发展出来的一个性能更强大的文本编辑器。可以主动的将字体颜色辨别语法…...

【数据结构】万字深入浅出讲解单链表(附原码 | 超详解)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石. 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言实现数据结构 💬总结:希望你看完…...
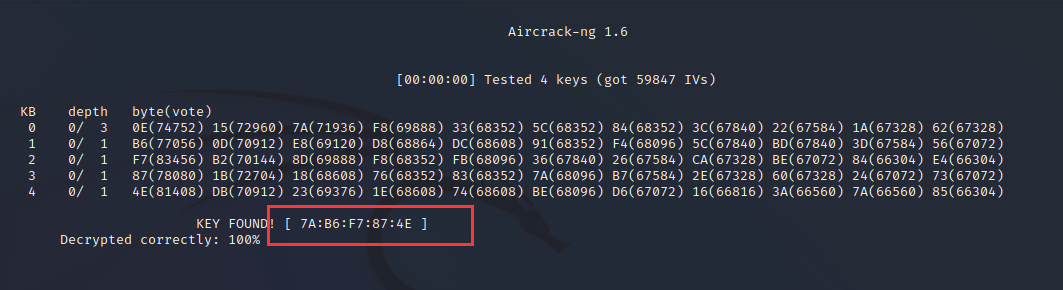
无线WiFi安全渗透与攻防(五)之aircrack-ng破解WEP加密
系列文章 无线WiFi安全渗透与攻防(一)之无线安全环境搭建 无线WiFi安全渗透与攻防(二)之打造专属字典 无线WiFi安全渗透与攻防(三)之Windows扫描wifi和破解WiFi密码 无线WiFi安全渗透与攻防(四)之kismet的使用 aircrack-ng破解WEP加密 1.WEP介绍 其实我们平常在使用wifi的时…...
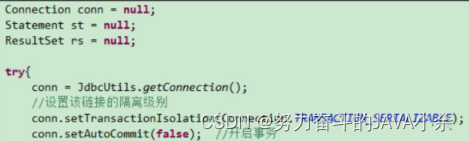
MySQL中事务的相关问题
事务 一、事务的概述: 1、事务处理(事务操作):保证所有事务都作为一个工作单元来执行,即使出现了故障,都不能改变这种执行方式。当在一个事务中执行多个操作时,要么所有的事务都被提交(commit…...

推荐算法再次踩坑记录
去年搞通了EasyRec这个玩意,没想到今年还要用推荐方面的东西,行吧,再来一次,再次踩坑试试。1、EasyRec训练测试数据下载:git clone后,进入EasyRec,然后执行:bash scripts/init.sh 将…...
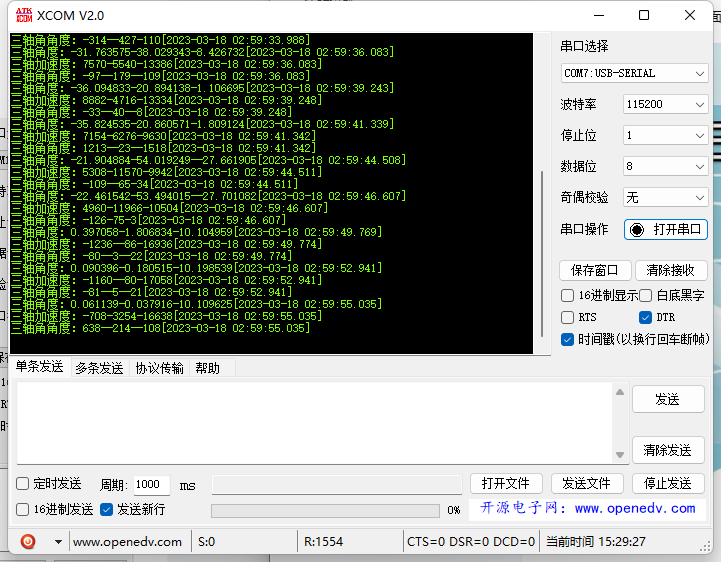
STM32 (十五)MPU6050
简介前言一、MPU6050简介MPU6050是一款性价比很高的陀螺仪,可以读取X Y Z 三轴角度,X Y Z 三轴加速度,还有内置的温度传感器,在姿态解析方面应用非常广泛。下面是它在淘宝上的参数图产品尺寸产品参数产品原理图:二、硬…...

使用yarn,依赖报各种错误怎么办
使用 yarn^3.x 版本时,默认并不会安装包到 node_modules,因为 yarn3.x 是即插即用的,也就是说如果你下载过这个包,yarn只会生成一个 Png文件,然后将包的路径 link 到下载过的地方,这样可以省去很多时间。而…...

面试官:rem和vw有什么区别
"rem" 和 "vw"的区别 "rem" 和 "vw" 都是用于网页设计的CSS单位。 "rem" 是相对于根元素的字体大小来计算的单位,即相对于 "html" 标签的字体大小。例如,如果 "html" 标签的字…...

【GPT-4】GPT-4 相关内容总结
目录 编辑 官网介绍 GPT-4 内容提升总结 GPT-4 简短版总结 GPT-4 基础能力 GPT-4 图像处理 GPT-4 技术报告 训练过程 局限性 GPT-4 风险和应对措施 开源项目:OpenAI Evals 申请 GPT-4 API API的介绍以及获取 官网介绍 官网:GPT-4 API候…...

5.springcloud微服务架构搭建 之 《springboot集成Hystrix》
1.springcloud微服务架构搭建 之 《springboot自动装配Redis》 2.springcloud微服务架构搭建 之 《springboot集成nacos注册中心》 3.springcloud微服务架构搭建 之 《springboot自动装配ribbon》 4.springcloud微服务架构搭建 之 《springboot集成openFeign》 目录 1.项目…...
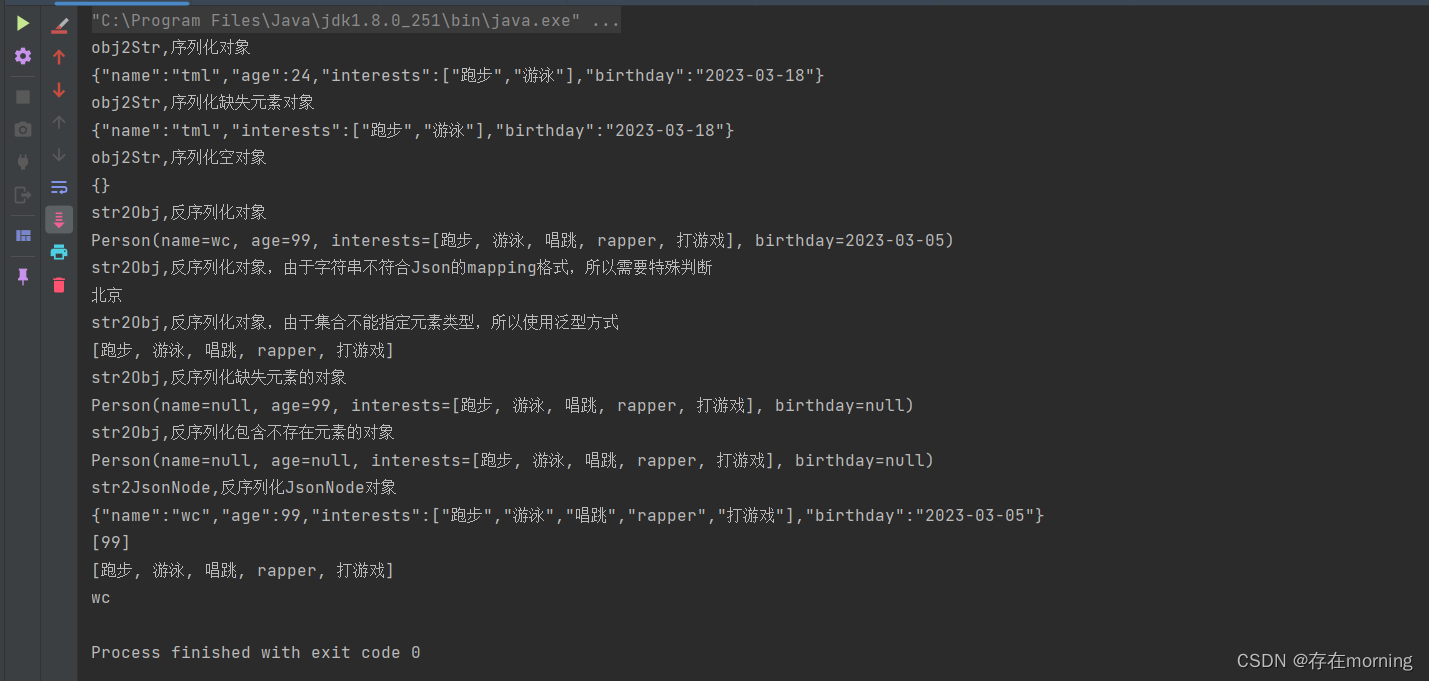
【工作中问题解决实践 七】SpringBoot集成Jackson进行对象序列化和反序列化
去年10月份以来由于公司和家里的事情太多,所以一直没有学习,最近缓过来了,学习的脚步不能停滞啊。回归正题,其实前年在学习springMvc的时候也学习过Jackson【Spring MVC学习笔记 五】SpringMVC框架整合Jackson工具,但是…...

香港服务器遭受DDoS攻击后如何恢复运行?
您是否发现流量异常上升?您的网站突然崩溃了吗?当您注意到这些迹象时,可能是在陷入了DDoS攻击的困境,因而,当开始考虑使用香港服务器时,也应该考虑香港服务器设备受DDoS攻击时,如何从中恢复。 在 DDoS 攻击香港…...
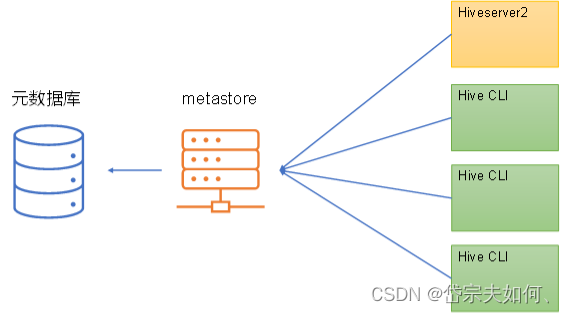
【Hive】配置
目录 Hive参数配置方式 参数的配置方式 1. 文件配置 2. 命令行参数配置 3. 参数声明配置 配置源数据库 配置元数据到MySQL 查看MySQL中的元数据 Hive服务部署 hiveserver2服务 介绍 部署 启动 远程连接 1. 使用命令行客户端beeline进行远程访问 metastore服务 …...

IP-GUARD如何强制管控电脑设置开机密码要符合密码复杂度?
如何强制管控电脑设置开机密码要符合密码复杂度? 7 可以在控制台-【策略】-【定制配置】,添加一条配置,开启系统密码复杂度检测。 类别:自定义 关键字:bp_password_complexity 内容:1 效果图:...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
