Pytorch使用教学7-张量的广播

PyTorch中的张量具有和NumPy相同的广播特性,允许不同形状的张量之间进行计算。
广播的实质特性,其实是低维向量映射到高维之后,相同位置再进行相加。我们重点要学会的就是低维向量如何向高维向量进行映射。
相同形状的张量计算
虽然我们觉得不同形状之间的张量计算才是广播,但其实相同形状的张量计算本质上也是广播。
t1 = torch.arange(3)
t1
# tensor([0, 1, 2])# 对应位置元素相加
t1 + t1
# tensor([0, 2, 4])
与Python对比
如果两个list相加,结果是什么?
a = [0, 1, 2]
a + a
# [0, 1, 2, 0, 1, 2]
不同形状的张量计算
广播的特性是不同形状的张量进行计算时,一个或多个张量通过隐式转化成相同形状的两个张量,从而完成计算。
但并非任意两个不同形状的张量都能进行广播,因此我们要掌握广播隐式转化的核心依据。
2.1 标量和任意形状的张量
标量(零维张量)可以和任意形状的张量进行计算,计算过程就是标量和张量的每一个元素进行计算。
# 标量与一维向量
t1 = torch.arange(3)
# tensor([0, 1, 2])t1 + 1 # 等效于t1 + torch.tensor(1)
# tensor([1, 2, 3])
# 标量与二维向量
t2 = torch.zeros((3, 4))
t2 + 1 # 等效于t2 + torch.tensor(1)
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
2.2 相同维度,不同形状张量之间的计算
我们以t2为例来探讨相同维度、不同形状的张量之间的广播规则。
t2 = torch.zeros(3, 4)
t2
# tensor([[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]])t21 = torch.ones(1, 4)
t21
# tensor([[1., 1., 1., 1.]])
它们都是二维矩阵,t21的形状是1×4,t2的形状是3×4,它们在第一个分量上取值不同,但该分量上t21取值为1,因此可以进行广播计算:
t2 + t21
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
而t2和t21的实际计算过程如下:

可理解为t21的一行与t2的三行分别进行了相加。而底层原理为t21的形状由1×4拓展成了t2的3×4,然后二者对应位置进行了相加。
t22 = torch.ones(3, 1)
t22
# tensor([[1.],
# [1.],
# [1.]])t2 + t22
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
同理,t22+t2与t21+t2结果相同。如果矩阵的两个维度都不相同呢?
t23 = torch.arange(3).reshape(3, 1)
t23
# tensor([[0],
# [1],
# [2]])t24 = torch.arange(3).reshape(1, 3)
# tensor([[0, 1, 2]])t23 + t24
# tensor([[0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])
此时,t23的形状是3×1,而t24的形状是1×3,二者的形状在两个份量上均不同,但都有1存在,因此可以广播:

如果两个张量的维度对应数不同且都不为1,那么就无法广播。
t25 = torch.ones(2, 4)
# t2的shape为3×4
t2 + t25
# RuntimeError
高维张量的广播
高维张量的广播原理与低维张量的广播原理一致:
t3 = torch.zeros(2, 3, 4)
t3
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])t31 = torch.ones(2, 3, 1)
t31
# tensor([[[1.],
# [1.],
# [1.]],# [[1.],
# [1.],
# [1.]]])t3+t31
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
总结
维度相同时,如果对应分量不同,但有一个为1,就可以广播。
不同维度计算中的广播
对于不同维度的张量,我们首先可以将低维的张量升维,然后依据相同维度不同形状的张量广播规则进行广播。
低维向量的升维也非常简单,只需将更高维度方向的形状填充为1即可:
# 创建一个二维向量
t2 = torch.arange(4).reshape(2, 2)
t2
# tensor([[0, 1],
# [2, 3]])# 创建一个三维向量
t3 = torch.zeros(3, 2, 2)
t3t2 + t3
# tensor([[[0., 1.],
# [2., 3.]],# [[0., 1.],
# [2., 3.]],# [[0., 1.],
# [2., 3.]]])
t3和t2的相加,就相当于1×2×2和3×2×2的两个张量进行计算,广播规则与低维张量一致。
相信看完本节,你已经充分掌握了广播机制的运算规则:
- 维度相同时,如果对应分量不同,但有一个为1,就可以广播
- 维度不同时,只需将低维向量的更高维度方向的形状填充为1即可
Pytorch张量操作大全:
Pytorch使用教学1-Tensor的创建
Pytorch使用教学2-Tensor的维度
Pytorch使用教学3-特殊张量的创建与类型转化
Pytorch使用教学4-张量的索引
Pytorch使用教学5-视图view与reshape的区别
Pytorch使用教学6-张量的分割与合并
Pytorch使用教学7-张量的广播
Pytorch使用教学8-张量的科学运算
Pytorch使用教学9-张量的线性代数运算
Pytorch使用教学10-张量操作方法大总结

相关文章:

Pytorch使用教学7-张量的广播
PyTorch中的张量具有和NumPy相同的广播特性,允许不同形状的张量之间进行计算。 广播的实质特性,其实是低维向量映射到高维之后,相同位置再进行相加。我们重点要学会的就是低维向量如何向高维向量进行映射。 相同形状的张量计算 虽然我们觉…...

生成式AI:对话系统(Chat)与自主代理(Agent)的和谐共舞
生成式AI:对话与行动的和谐共舞 我们正站在一个令人激动的时代门槛上——生成式AI技术飞速发展,带来了无限的可能性。一个关键问题浮现:AI的未来是对话系统(Chat)的天下,还是自主代理(Agent&am…...
唯众物联网(IOT)全功能综合实训教学解决方案
一、引言 在信息技术日新月异的今天,物联网(IoT)作为推动数字化转型的关键力量,其触角已延伸至我们生活的方方面面,深刻地重塑了工作模式、生活习惯乃至社会结构的每一个角落。面对这一前所未有的变革浪潮,…...

24证券从业考试报名『个人信息表』填写模板❗
24证券从业考试报名『个人信息表』填写模板❗ 1️⃣居住城市、通讯地址:写自己现居住的地址就可以。 2️⃣学历:需要注意的是学历填写的是考生已经取得的学历,在校大学生已经不具有报名资格,选择大专以上,或者是高中学…...

深度学习系列70:模型部署torchserve
1. 流程说明 ts文件夹下, 从launcher.py进入,执行jar文件。 入口为model_server.py的start()函数。内容包含: 读取args,创建pid文件 找到java,启动model-server.jar程序,同时读取log-config文件ÿ…...
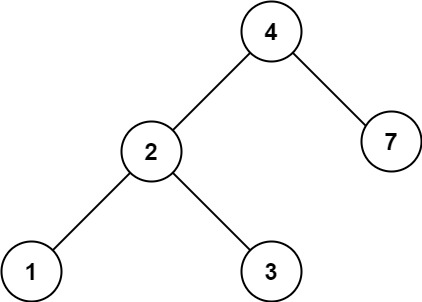
算法日记day 20(中序后序遍历序列构造二叉树|最大、合并、搜索二叉树)
一、中序后序序列构造二叉树 题目: 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,…...

【科研】# Taylor Francis 论文 LaTeX template模版 及 Word模版
【科研写论文】系列 文章目录 【科研写论文】系列前言一、Word 模板(附下载网址):二、LaTeX 版本方法1:直接网页端打开(附网址)方法2:直接下载到本地电脑上编辑下载地址说明及注意事项 前言 给…...

Linux网络配置及常见命令!
vim /etc/sysconfig/network-scripsts/ifcfg-ens33(图形界面配置网络) Xshell rz:上传(从Windows到Linux) sz:下载:(从Linux到Windows)(后接文件手工输入)…...

linux之shell脚本实战
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:Linux运维老纪的首页…...

文件上传漏洞(ctfshow web151-161)
Web151 F12修改源代码 exts后面png改为php 这样就可以上传php的文件了 Web152: 考点:后端不能单一校验 就是要传图片格式,抓个包传个png的图片 然后bp抓包修改php后缀解析 然后放包 Web153-web156 在php代码中可以使用“{}”代替“[]” …...

小猪佩奇.js
闲着没事 使用js 画一个小猪佩奇把 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</tit…...
人工智能AI合集:Ollama部署对话语言大模型-网页访问
目录 🍅点击这里查看所有博文 随着人工智能技术的飞速发展,AI已经不再是遥不可及的高科技概念,而是逐渐融入到我们的日常生活中。从智能手机的语音助手到家庭中的智能音箱,再到工业自动化和医疗诊断,AI的应用无处不在…...

CentOS搭建Apache服务器
安装对应的软件包 [roothds ~]# yum install httpd mod_ssl -y 查看防火墙的状态和selinux [roothds ~]# systemctl status firewalld [roothds ~]# cat /etc/selinux/config 若未关闭,则关闭防火墙和selinux [roothds ~]# systemctl stop firewalld [roothds ~]# …...

CDGA|数据治理:安全如何贯穿数据供给、流通、使用全过程
随着信息技术的飞速发展,数据已经成为企业运营、社会管理和经济发展的核心要素。然而,数据在带来巨大价值的同时,也伴随着诸多安全风险。因此,数据治理的重要性日益凸显,它不仅仅是对数据的简单管理,更是确…...

32单片机bootloader程序
一,单片机为什么要使用bootloader 1、使用bootloader的好处 1) 程序隔离:可以同时存在多个程序,只要flash空间够大,或者通过外挂flash,可以实现多个程序共存,在多个程序之间切换使用。 2)方便程…...

MongoDB - 数组更新操作符:$、$[]、$pop、$pull、$push、$each、$sort、$slice、$position
文章目录 1. $1. 更新数组中的值2. 更新数组中的嵌入文档 2. $[]1. 更新数组中的所有元素2. 更新数组中的所有嵌入文档 3. $pop1. 删除数组的第一个元素2. 删除数组的最后一个元素 4. $pull1. 删除所有等于指定值的项2. 删除与指定条件匹配的所有项3. 从文档数组中删除项4. 从嵌…...

多GPU并行处理[任务分配、进程调度、资源管理、负载均衡]
1. 多GPU并行处理设计 设计思路: 实现基于多GPU的并行任务处理,每个GPU运行独立的任务,以加速整体的处理速度。 实现机制: 进程隔离: 利用multiprocessing.Process为每个GPU创建独立的工作进程。 GPU资源限制: 通过设置CUDA_VISIBLE_DEVICES环境变量&…...

项目部署到服务器
(相关资源都给出来了) 1 下载MobaXterm,然后打开 正常连接输入你的服务器IP,用户名可以起名为root 2 将JDK,Tomcat,mysql安装包 布置到服务器中(JDK官网地址:https://www.oracle.com/java/technologies/downloads/#java8 mysql官网地址: …...

Idea2024 创建Meaven项目没有src文件夹
1、直接创建 新建maven项目,发现没有src/main/java 直接新建文件夹:右击项目名->new->Directory 可以看到idea给出了快捷创建文件夹的选项,可以根据需要创建,这里点击src/main/java 回车,可以看到文件夹已经创建…...

LeetCode 2766.重新放置石块:哈希表
【LetMeFly】2766.重新放置石块:哈希表 力扣题目链接:https://leetcode.cn/problems/relocate-marbles/ 给你一个下标从 0 开始的整数数组 nums ,表示一些石块的初始位置。再给你两个长度 相等 下标从 0 开始的整数数组 moveFrom 和 moveTo…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
