Android 开发中px、dpi 和 dp三个单位的介绍
Android 开发中px、dpi 和 dp三个单位的介绍
在 Android 开发中,px、dpi 和 dp 是用来描述屏幕尺寸和密度的单位,它们在设计和开发中有着不同的作用和用途。
1. px(像素)
-
定义:
px表示屏幕上的一个像素点,是最小的显示单位。在 Android 开发中,屏幕上的所有元素都是以像素为单位进行显示和布局的。 -
使用场景: 在编写布局文件时,通常使用
px来定义元素的大小和位置,如layout_width="100px"。 -
注意事项: 使用
px作为单位可以精确控制元素在屏幕上的大小和位置,但需要考虑不同密度设备上的适配问题。
2. dpi(屏幕密度)
-
定义:
dpi(dots per inch,每英寸像素数)表示屏幕每英寸的像素密度,是衡量屏幕显示精细度的单位。 -
分类: Android 将设备根据屏幕密度分为几个主要类别:
ldpi(低密度,约 120dpi)mdpi(中密度,约 160dpi)hdpi(高密度,约 240dpi)xhdpi(超高密度,约 320dpi)xxhdpi(超超高密度,约 480dpi)xxxhdpi(超超超高密度,约 640dpi)
-
使用场景: 在 Android 开发中,可以根据不同的屏幕密度提供对应的资源(如图标、图片)来适配不同密度的设备。
3. dp(密度无关像素)
-
定义:
dp(density-independent pixels,密度无关像素)是 Android 开发中推荐使用的单位,它可以根据不同密度的设备进行适配。 -
转换关系:
dp和px之间的转换关系是通过设备的屏幕密度来确定的,通常可以使用公式px = dp * (dpi / 160)进行转换。 -
使用场景: 在编写布局文件时,应尽量使用
dp单位来定义元素的大小和间距,以确保在不同密度设备上显示时保持一致的物理尺寸和布局效果。
总结:
- px(像素): 最小的显示单位,用于精确控制元素大小和位置。
- dpi(屏幕密度): 表示屏幕每英寸的像素数,用于适配不同密度的设备。
- dp(密度无关像素): 建议使用的单位,可根据设备密度进行适配,用于定义布局大小和间距。
在 Android 开发中,理解和正确使用这些单位是确保应用在不同设备上良好显示和用户体验的关键。
相关文章:

Android 开发中px、dpi 和 dp三个单位的介绍
Android 开发中px、dpi 和 dp三个单位的介绍 在 Android 开发中,px、dpi 和 dp 是用来描述屏幕尺寸和密度的单位,它们在设计和开发中有着不同的作用和用途。 1. px(像素) 定义: px 表示屏幕上的一个像素点,…...

zookeeper开启SASL权限认证
目录 一、SASL介绍 二、使用 SASL 进行身份验证 2.1 服务器到服务器的身份验证 2.2 客户端到服务器身份验证 三、验证功能 一、SASL介绍 默认情况下,ZooKeeper 不使用任何形式的身份验证并允许匿名连接。但是,它支持 Java 身份验证与授权服务(JAAS)…...
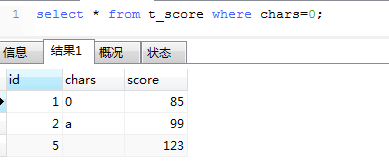
mysql一个小问题引发的思考-mysql类型转换-查询缓存 及 MYSQL查询缓存以及自动选择不使用查询缓存的情况
一、mysql一个小问题引发的思考-mysql类型转换-查询缓存 最近在做的一个项目中有一个SQL语句发现点问题,大概如下: select * from table where cid0 or find_in_set(1, cid); 数据表中的字段cid是字符串类型,原来的后端同学未提过此字段还能是…...

css更改图片颜色
css更改图片颜色,比较时候颜色单一的图片,比如logo之类的 css中的 filter 属性定义元素(通常是 <img>)的视觉效果(如模糊和饱和度) img{ -webkit-filter: invert(51%) sepia(94%) saturate(6433%) h…...

通过POST请求往Elastic批量插入数据
文章目录 引言I 请求文档请求参数请求例子引言 调试工具:Apifox 需求: 向Elasticsearch中的’test_index’索引批量插入文档 情况认证: Basic Auth 在 Header 添加参数 Authorization,其值为在 Basic 之后拼接空格,以及经过 Base64 编码的 {{Username}}:{{Password}} 示…...
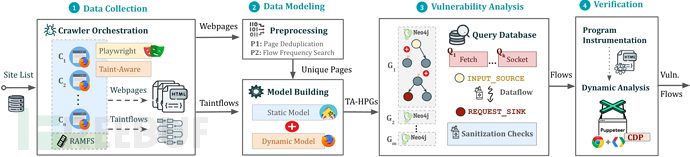
JAW:一款针对客户端JavaScript的图形化安全分析框架
关于JAW JAW是一款针对客户端JavaScript的图形化安全分析框架,该工具基于esprima解析器和EsTree SpiderMonkey Spec实现其功能,广大研究人员可以使用该工具分析Web应用程序和基于JavaScript的客户端程序的安全性。 工具特性 1、动态可扩展的框架&#x…...

错误解决 error CS0117: ‘Buffer‘ does not contain a definition for ‘BlockCopy‘
Unity 2022.3.9f1 导入 Runtime OBJ Importer 后出现: error CS0117: ‘Buffer’ does not contain a definition for ‘BlockCopy’ 解决办法: 源代码: int DDS_HEADER_SIZE 128; byte[] dxtBytes new byte[ddsBytes.Length - DDS_HEAD…...

ICMPv6与DHCPv6之网络工程师软考中级
ICMPv6概述 ICMPv6是IPv6的基础协议之一。 在IPv6报文头部中,Next Header字段值为58则对应为ICMPv6报文。 ICMPv6报文用于通告相关信息或错误。 ICMPv6报文被广泛应用于其它协议中,包括NDP、Path MTU发现机制等 ICMPv6控制着IPv6中的地址自动配置、地址…...

【HTML — 构建网络】HTML 入门
在本文中,我们将介绍 HTML 的绝对基础知识。为了帮助您入门,本文定义了元素、属性以及您可能听说过的所有其他重要术语。它还解释了这些在 HTML 中的位置。您将学习 HTML 元素的结构、典型的 HTML 页面的结构以及其他重要的基本语言功能。在此过程中,也将有机会玩转 HTML! …...

javafx的ListView代入项目的使用
目录 1. 创建一个可观察的列表,用于存储ListView中的数据,这里的User是包装了用户的相关信息。 2.通过本人id获取friendid,及好友的id,然后用集合接送,更方便直观一点。 3.用for遍历集合,逐个添加。 4.渲染器&…...

基于ABAP OLE技术实现对服务器文件进行读写操作
使用ABAP中的OLE(Object Linking and Embedding)技术,可以实现对服务器文件的读写操作。以下是一个示例,演示如何通过ABAP代码使用OLE自动化对象来读写服务器上的文件。这里主要以Excel文件的读写操作为例。 1. 读Excel文件 代码…...
字段的预处理解决方案)
求教Postgresql在jdbc处理bit(1)字段的预处理解决方案
文章目录 1.建表语句:2.使用以下方式的预处理方式都报错了3.可以先用sql拼接实现功能 1.建表语句: CREATE TABLE public.h_user (id serial4 not null,username varchar(50) NULL,"password" varchar(64) NULL,nickname varchar(60) NULL,ema…...

微信小程序-自定义tabBar
通过官网给出的示例自己实现了自定义的tabBar,但结果发现 无法监听页面生命周期函数 结语:原想的是实现不一样的效果(如下) 故尝试了自定义tabBar,虽然做出来了,但也发现这个做法存在不足: 在…...

vue3+element-plus 实现动态菜单和动态路由的渲染
在 Vue.js 中,使用 Vue Router 管理路由数据,并将其用于渲染 el-menu(Element UI 的菜单组件)通常涉及以下几个步骤: 定义路由元数据: 在你的路由配置中,为每个路由项添加 meta 字段,…...

GO-学习-03-基本数据类型
数据类型:基本数据类型和复合数据类型 基本数据类型:整型、浮点型、布尔型、字符串 复合数据类型:数组、切片、结构体、函数、map、通道(channel)、接口 整型: package main import "fmt" im…...

高并发场景下,系统的保护机制
伴随着分布式,微服务项目的快速发展。各个微服务的调用和通讯难免会出现依赖关系,如果上游服务在依赖下游服务的时候下游服务出现了故障从而导致下游服务的不可用,进一步导致了上游的服务被拖垮,就会发生服务雪崩,故障…...
)
服务器构建私有npm库(Docker + Verdaccio)
npm官网有时候因为网络原因包推不上去,那就简单构建个私有库 私有库不会被共享,且配置不需要太高1h2G就行 1.需要安装Docker,这个跳过了 2.生成配置文件 mkdir /home/verdaccio cd /home/verdaccio mkdir conf && mkdir storage &am…...

LabVIEW做二次开发时应该注意哪些方面?
在使用LabVIEW进行二次开发时,以下几个方面需要特别注意: 需求明确化: 确认并详细记录客户的需求,明确系统的功能、性能、可靠性等要求。制定详细的需求文档,并与客户反复确认,避免后期的需求变更和误解。 …...

docker配置上网代理获取镜像
一、添docker子配置档设置 1、创建目录 mkdir /etc/systemd/system/docker.service.d 2、创建http-proxy.conf文件,增加以下内容 cat > /etc/systemd/system/docker.service.d/http-proxy.conf <<EOF [Service] Environment“HTTP_PROXYhttp://192.168.0.2:8118…...

SqlSugar删除没有定义主键的实体类对应的数据库表数据
一般而言,使用SqlSugar的DbFirst功能创建数据库表实体类时,如果数据库表有主键,生成的实体类对应属性也会标识为主键,如下图所示。 但有时候生成的实体类没有自动配置主键,这时可以通过以下方式进行删除操作&…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
