面试重点---快速排序
快排单趟
快速排序是我们面试中的重点,这个知识点也很抽象,需要我们很好的掌握,而且快速排序的代码也是非常重要,需要我们懂了还不行,必须要手撕代码,学的透彻。
在研究快速排序之前,我们首先看一个动画,先自己看几遍,看能不能看懂它在干什么。
这个动画就是我们快排的总体过程,如果你没有看懂也不用急,我用文字来帮助你理解这个过程。我们定义了一个key,他是6这个数字,然后L和R分别在数组的最左边和最右边,首先让R先走,让R找到比key小的数,第一个找的是5,然后不动,再让L向右移动,找到比key大的数,不动,将L和R交换,再继续移动,直到L和R相遇,相遇之后,与key交换,就达到了下面这幅图的效果。

仔细观察可以发现,我们的6到达了它应该到达的位置,并且,6的左边都比6小,6的右边都比6大。这是我们快排的单趟过程。
快排的全过程
上面我们研究了快排的单趟,而我们怎么将它的单趟结合起来,让整个数组的顺序都排好呢?下面我们来看一组图,演示一下快排的全过程。
这就是快速排序的全过程,是不是很熟悉,就是我们之前二叉树里面接触的递归,有没有想起来呢?
这就是我们实现快排的过程。
key的选取
首先我们思考一个问题,当我们的数组是有序的,那么,效率会发生什么变化呢?
是不是就像上图一样,我们这个时间复杂度就从N*logN变成了N^2呢?效率瞬间就下降了一个层次,为了避免这样的情况发生,我们思考的解决方案就是将我们选取的k不固定的选在第一个,这样就避免了上图的样子,效率也会蹭蹭往上涨,那么,k 用什么办法选呢?
第一种方法就是随机选取,第二种方法就是取中间值,我个人认为还是第二种科学一点,第二种方法的k值是可控的,科学的,不是随机生成的。
全部代码见下篇文章。
相关文章:

面试重点---快速排序
快排单趟 快速排序是我们面试中的重点,这个知识点也很抽象,需要我们很好的掌握,而且快速排序的代码也是非常重要,需要我们懂了还不行,必须要手撕代码,学的透彻。 在研究快速排序之前,我们首先…...
[MIT6.5840]MapReduce
MapReduce Lab 地址 https://pdos.csail.mit.edu/6.824/labs/lab-mr.html 论文地址 https://static.googleusercontent.com/media/research.google.com/zh-CN//archive/mapreduce-osdi04.pdf 工作原理 简单来讲,MapReduce是一种分布式框架,可以用来处理…...

【系统架构设计师】计算机组成与体系结构 ⑯ ( 奇偶校验码 | CRC 循环冗余码 | 海明码 | 模 2 除法 )
文章目录 一、校验码1、校验码由来2、奇偶校验码3、CRC 循环冗余码 ( 重点考点 )4、海明码校验 ( 软考不经常考到 ) 二、CRC 循环冗余码 ( 重点考点 )1、模 2 除法概念2、模 2 除法步骤3、模 2 除法示例4、CRC 循环冗余码示例 15、CRC 循环冗余码示例 2 参考之前的博客 : 【计…...

springboot,service 层统一异常抛出时,throws Exception写在接口上还是实现类上
springboot,service 层统一异常抛出时,throws Exception写在实现接口上,不是直接写在实现类上...

深度学习高效性网络
为了减轻Transformer笨重的计算成本,一系列工作重点开发了高效的Vision Transformer,如Swin Transformer、PVT、Twins、CoAtNet和MobileViT。 1、字节TRT-ViT 兼具CNN的速度、Transformer精度的模型 TRT-ViT(Transformer-based Vision Tra…...

PyQt ERROR:ModuleNotFoundError: No module named ‘matplotlib‘
Solution:打开cmd输入指令下载malplotlib pip install matplotlib...

Flutter Geolocator插件使用指南:获取和监听地理位置
Flutter Geolocator插件使用指南:获取和监听地理位置 简介 geolocator 是一个Flutter插件,提供了一个简单易用的API来访问特定平台的地理位置服务。它支持获取设备的最后已知位置、当前位置、连续位置更新、检查设备上是否启用了位置服务,以…...

网站基本布局CSS
代码 <!DOCTYPE html> <html> <head><meta charset"utf-8"><meta name"viewport" content"widthdevice-width, initial-scale1"><title></title><style type"text/css">body {margi…...

ssm框架整合,异常处理器和拦截器(纯注解开发)
目录 ssm框架整合 第一步:指定打包方式和导入所需要的依赖 打包方法:war springMVC所需依赖 解析json依赖 mybatis依赖 数据库驱动依赖 druid数据源依赖 junit依赖 第二步:导入tomcat插件 第三步:编写配置类 SpringCon…...
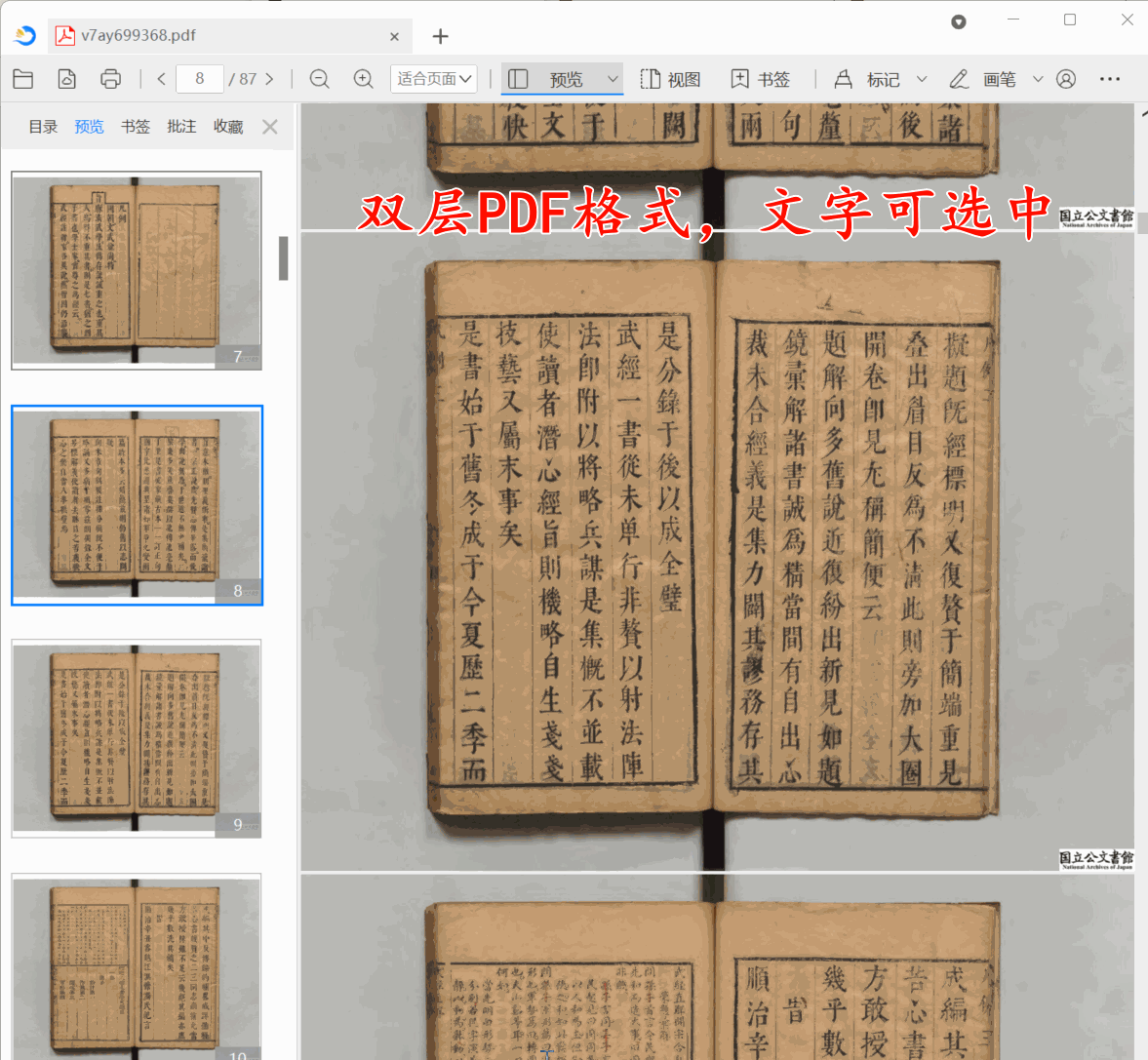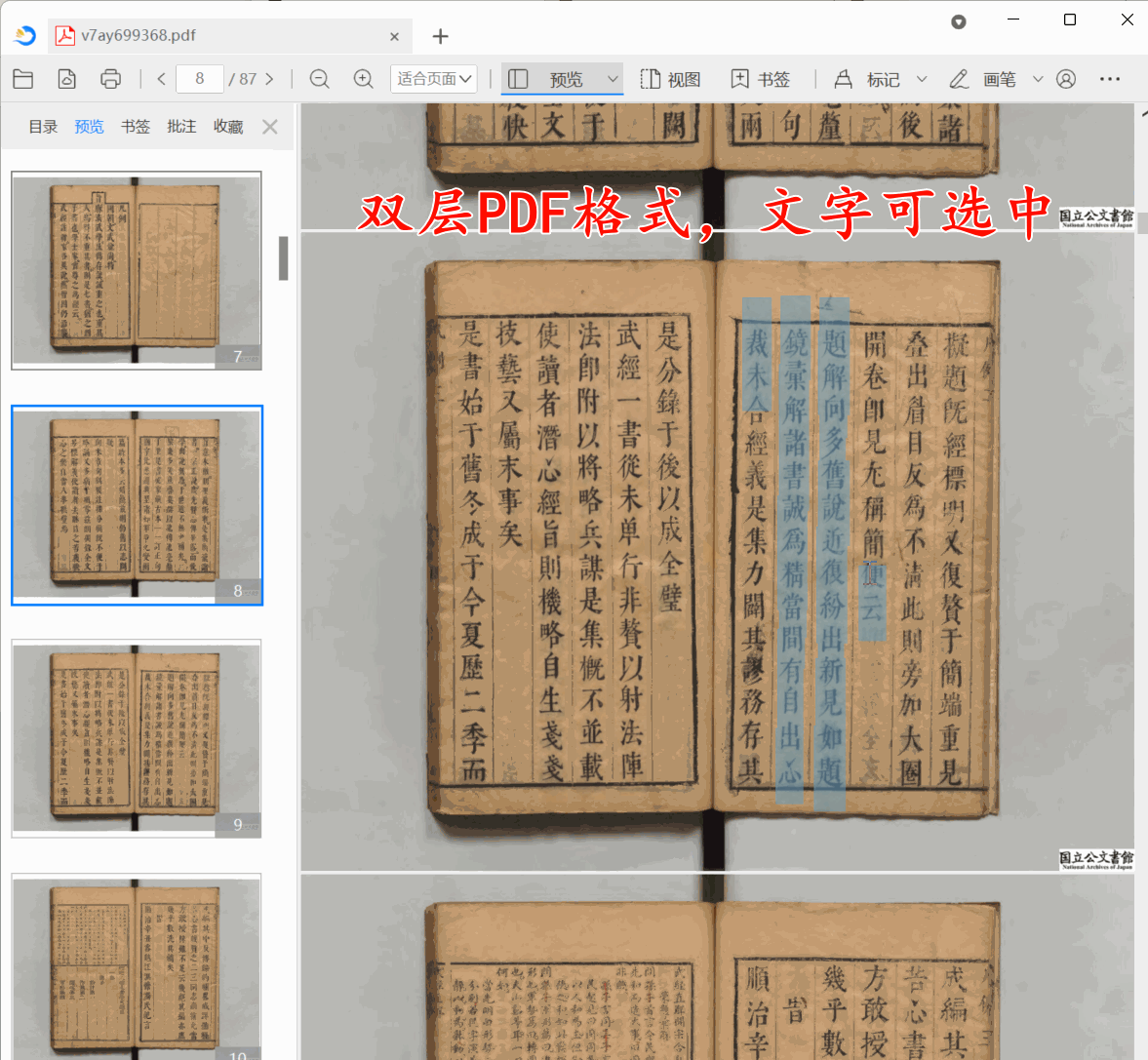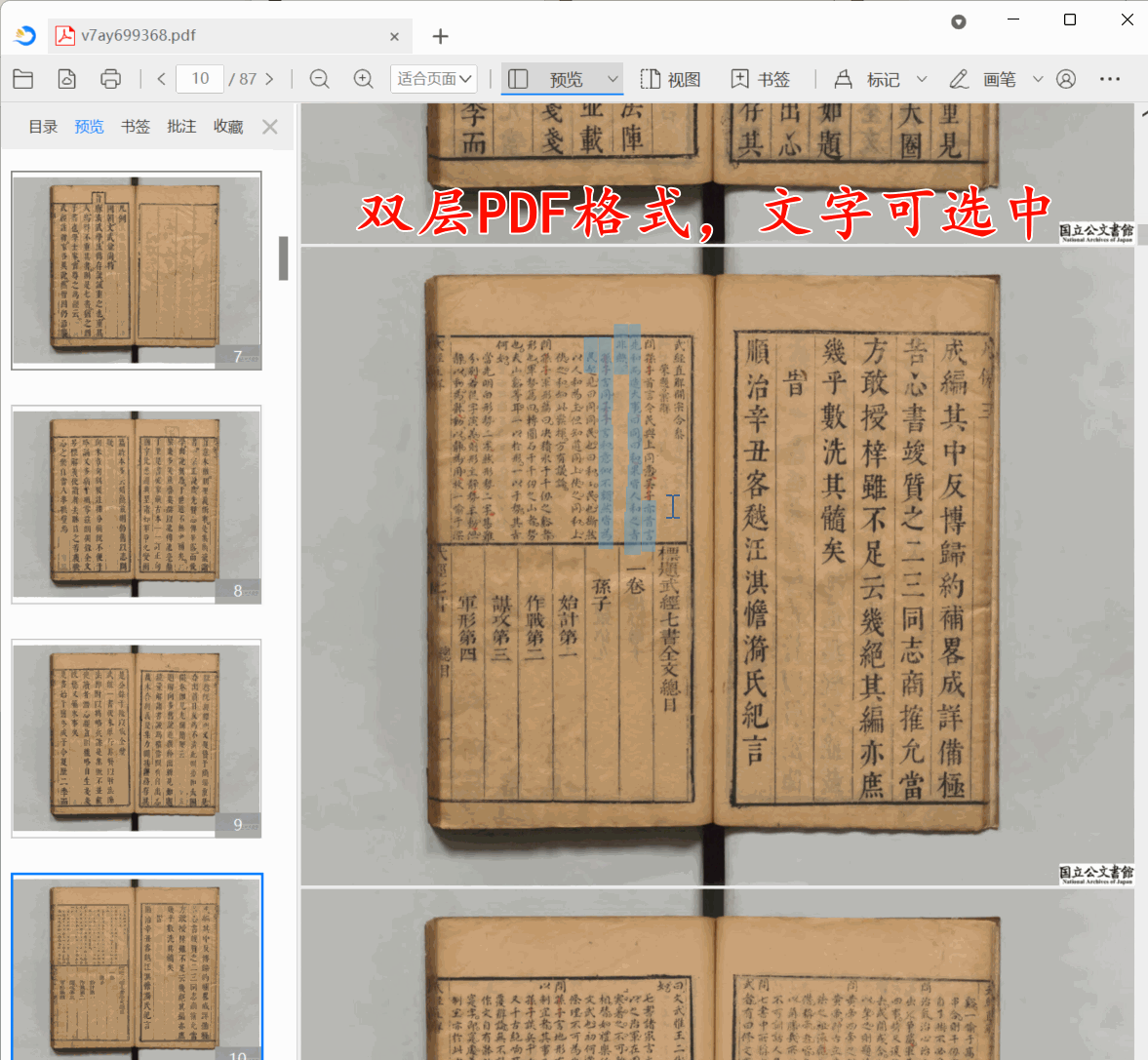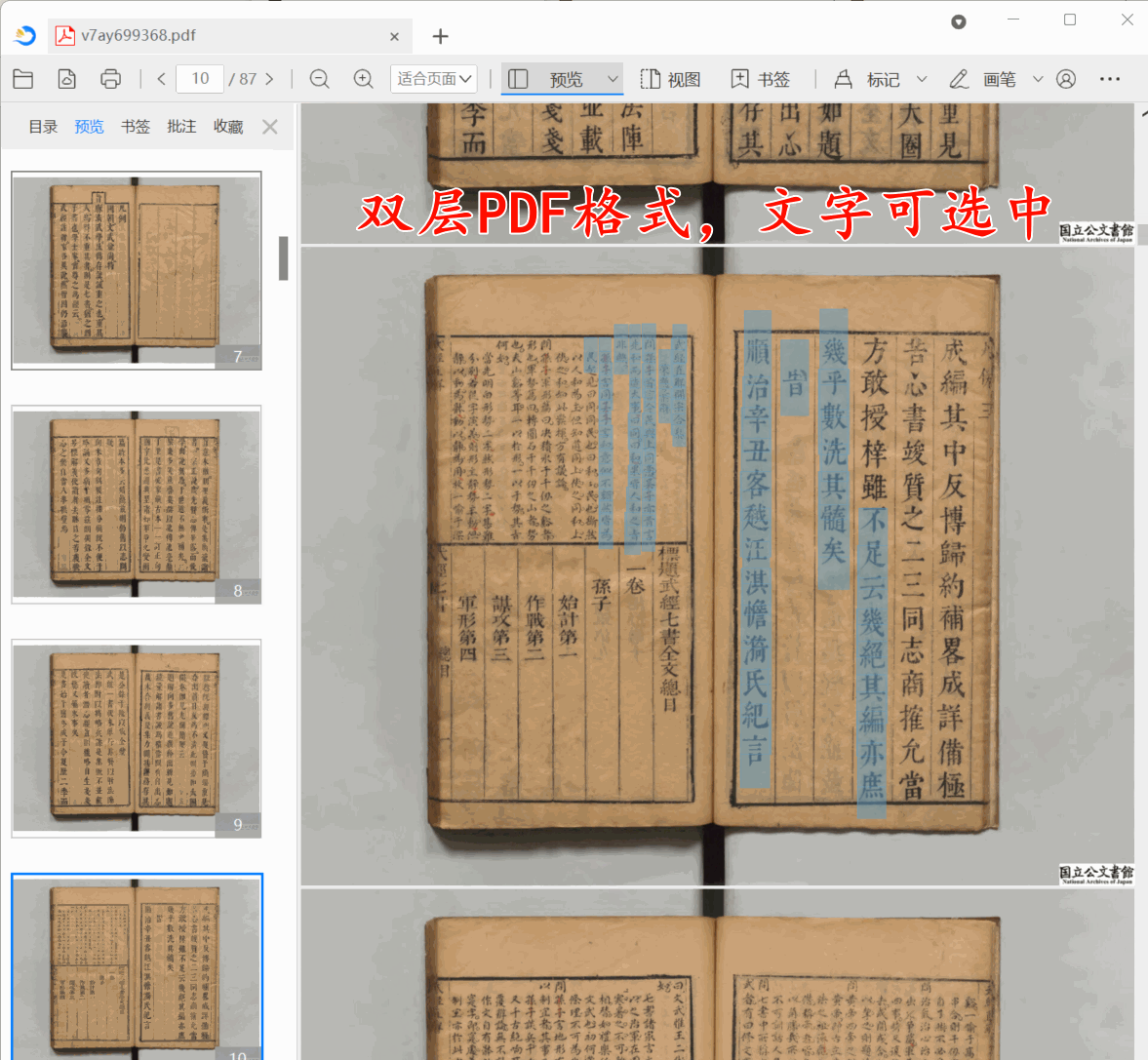
古籍双层PDF制作教程:保姆级古籍数字化教程
在智慧古籍数字化项目中,很多图书馆要求将古籍导出为双层PDF,并且确保输出双层PDF底层文本与上层图片偏移量控制在1毫米以内。那么本教程带你使用古籍数字化平台,3分钟把一个古籍书籍转化为双侧PDF。 第1步:上传古籍 点批量上传…...

Git 删除 远端的分支
要删除 Git 远端的分支(例如: V3.2.1.13): 可以执行以下命令 git push origin --delete V3.2.1.13这条命令会向远端的仓库删除名为 V3.2.1.13 的分支。如果这个分支只在远端仓库存在而没有对应的本地分支,那么删除后这…...

PrgogressBar实现原理分析
ProgressBar 是 Android 中用于显示进度条的控件,它可以用来表示任务的完成程度或者加载进度等信息。ProgressBar 有两种主要类型:一种是确定性的(determinate),另一种是不确定性的(indeterminateÿ…...

【HarmonyOS】HarmonyOS NEXT学习日记:七、页面与组件的生命周期
【HarmonyOS】HarmonyOS NEXT学习日记:七、页面与组件的生命周期 页面和组件 组件:用Component装饰的代码称为自定义组件页面:Entry装饰的组件即页面的根节点 组件生命周期 aboutToAppear:在创建自定义组件的新实例后…...

【iOS】——Block循环引用
循环引用原因 如果在Block中使用附有_ _strong修饰符的对象类型自动变量,那么当Block从栈复制到堆时,该对象为Block所持有,这样容易引起循环引用。 HPPerson *person [[HPPerson alloc] init];person.block ^{NSLog("person.age--- …...

shell脚本自动化安装启动各种服务
1、自动化配置dns服务器 A主机:vim dns.sh #!/bin/bash# 自动化部署dns# 1、下载bind# 2、修改配置文件# vim /etc/named.conf # listen-on port 53 { 127.0.0.1;any; }; 修改(定位替换)# allow-query { localhost;any; }; 修改&am…...

Python - 开源库 ReportLab 库合并 CVS 和图像生成 PDF 文档
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/140281680 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 Report…...

Java编写SIP协议
1、编写Server代码 package com.genersoft.iot.vmp.sip; import javax.sip.*; import javax.sip.message.*; import javax.sip.header.*; import java.util.*;public class SimpleSipServer implements SipListener {private SipFactory sipFactory;private SipStack sipStack…...

大型语言模型LLM的核心概念
本文主要介绍了目前主流的,几个大型语言模型LLM的整个训练过程 通常分为下面的几个阶段 1. 预训练 采用互联网上的大量数据进行训练,这一阶段大模型LLM的主体已定,找出共性并且压缩成一个模型。模型的参数量不是越大越好,遵循合理…...

软件测试---网络基础、HTTP
一、网络基础 (1)Web和网络知识 网络基础TCP/IP 使用HTTP协议访问Web WWW万维网的诞生 WWW万维网的构成 (2)IP协议 (3)可靠传输的TCP和三次握手策略 (4)域名解析服务DNS ࿰…...

韩顺平0基础学java——第39天
p820-841 jdbc和连接池 1.JDBC为访问不同的数据库提供了统一的接口,为使用者屏蔽了细节问题。 2.Java程序员使用JDBC,可以连接任何提供了JDBC驱动程序的数据库系统,从而完成对数据库的各种操作。 3.jdbc原理图 JDBC带来的好处 2.JDBC带来的…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
