【强化学习的数学原理】课程笔记--5(值函数近似,策略梯度方法)
目录
- 值函数近似
- 一个例子
- TD 算法的值函数近似形式
- Sarsa, Q-learning 的值函数近似形式
- Deep Q-learning
- experience replay
- 策略梯度方法(Policy Gradient)
- Policy Gradient 的目标函数
- 目标函数 1
- 目标函数 2
- 两种目标函数的同一性
- Policy Gradient 目标函数的梯度
- Policy Gradient 目标函数梯度的统一形式
- discounted case 情形下的目标函数梯度
- undiscounted case 情形下的目标函数梯度
- 蒙特卡洛 policy gradient ( REINFORCE 算法)
系列笔记:
【强化学习的数学原理】课程笔记–1(基本概念,贝尔曼公式)
【强化学习的数学原理】课程笔记–2(贝尔曼最优公式,值迭代与策略迭代)
【强化学习的数学原理】课程笔记–3(蒙特卡洛方法)
【强化学习的数学原理】课程笔记–4(随机近似与随机梯度下降,时序差分方法)
值函数近似
回忆前面章节所介绍的各种强化学习算法,在求解 state value 和 action value 时:
v π = [ v π ( s 1 ) , v π ( s 2 ) , ⋯ , v π ( s n ) ] v_{\pi} = \left[ v_{\pi}(s_1), v_{\pi}(s_2), \cdots, v_{\pi}(s_n) \right] vπ=[vπ(s1),vπ(s2),⋯,vπ(sn)]
q π = [ q π ( s 1 , a 1 ) q π ( s 1 , a 2 ) ⋯ q π ( s 1 , a m ) q π ( s 2 , a 1 ) q π ( s 2 , a 2 ) ⋯ q π ( s 2 , a m ) ⋮ ⋮ ⋱ ⋮ q π ( s n , a 1 ) q π ( s n , a 2 ) ⋯ q π ( s n , a m ) ] q_{\pi} = \begin{bmatrix} q_{\pi}(s_1,a_1) & q_{\pi}(s_1,a_2) & \cdots & q_{\pi}(s_1,a_m) \\ q_{\pi}(s_2,a_1) & q_{\pi}(s_2,a_2) & \cdots & q_{\pi}(s_2,a_m) \\ \vdots & \vdots & \ddots & \vdots\\ q_{\pi}(s_n,a_1) & q_{\pi}(s_n,a_2) & \cdots & q_{\pi}(s_n,a_m) \end{bmatrix} qπ= qπ(s1,a1)qπ(s2,a1)⋮qπ(sn,a1)qπ(s1,a2)qπ(s2,a2)⋮qπ(sn,a2)⋯⋯⋱⋯qπ(s1,am)qπ(s2,am)⋮qπ(sn,am)
都是对上述一维或者二维向量 (后面统称 tabular)里的值一个个求解的。这样在实际使用中有一个问题,当 state space 以及 action space 非常大时,需要求解以及储存的未知量都会非常大。为了缓解这样的情况,因此提出了 值函数近似 的想法(NOTE:前面基于 tabular 的求解是精确求解,而这里的值函数是 近似 求解,相当于为了减少计算/存储量,牺牲了一定的精度)
一个例子
下面我们看一个例子,首先看一下用前面精确求解时得到的准确结果:

前面基于 tabular 的算法,求到的结果即是 ( b ) (b) (b)。这里为了方便理解,我们将 ( b ) (b) (b) 中的 tabular 画成了图像 ( c ) (c) (c),其中的底面对应的是 (state_index, action_index)。
那么值函数近似,即想拟合 ( c ) (c) (c) 中的图像。这里的图像明显是个高阶的曲面,且阶数约高,拟合得越好(因为高阶函数总可以拟合低阶的函数),但一味追求高阶会使得计算复杂度上升,相当于又回到了 tabular 的算法 (事实上,只要阶数够高,值函数是可以完全拟合 tabular 算法的)。所以下面我们进行几个实验,将阶数从低往高逐渐提升,来看值函数近似的效果:
线性值函数近似可以写成:
v ^ ( s , w ) = ϕ T ( s ) w ϕ ( s ) , w ∈ R n × 1 \hat v(s,w) = \phi^T(s) w\qquad \phi(s),w \in \mathbb{R}^{n \times 1} v^(s,w)=ϕT(s)wϕ(s),w∈Rn×1
其中 ϕ T ( s ) \phi^T(s) ϕT(s) 是特征函数,用于描述函数的形式,例如:是直线,平面,还是 n 阶曲面。 w w w 则是要求的参数

图中从左到右,函数的阶分别为 1 阶,2 阶,3 阶:
ϕ ( 1 ) ( s ) = [ 1 , x , y ] ϕ ( 2 ) ( s ) = [ 1 , x , y , x 2 , y 2 , x y ] ϕ ( 3 ) ( s ) = [ 1 , x , y , x 2 , y 2 , x y , x 3 , y 3 , x 2 y , x y 2 ] \begin{aligned} \phi^{(1)}(s) &= [1, x, y]\\ \phi^{(2)}(s) &= [1, x, y, x^2, y^2, xy]\\ \phi^{(3)}(s) &= [1, x, y, x^2, y^2, xy, x^3, y^3, x^2y, xy^2] \end{aligned} ϕ(1)(s)ϕ(2)(s)ϕ(3)(s)=[1,x,y]=[1,x,y,x2,y2,xy]=[1,x,y,x2,y2,xy,x3,y3,x2y,xy2]
可以看到,阶数越高,对图像 ( c ) (c) (c) 的拟合越好,这意味着值函数近似求到的策略与最优策略越接近,但同时需要求解的参数也更多了( d i m ( w ) dim(w) dim(w) 分别为 3,6,10)。
泛化性
同时由于值函数近似的建模方式,在之前的 tabular-based 算法中,我们需要对每个 state 都访问足够多次,才能获得每个 state 较为准确的 state value,但值函数的建模方式,使得每个样本对于参数 w w w 的修改,都能作用于其他的 state,所以值函数近似相比 tabular-based 算法有更强的泛化性。
特征函数 ϕ ( s ) \phi(s) ϕ(s) 的选择
从上面的例子也不难发现,其实特征函数 ϕ ( s ) \phi(s) ϕ(s) 的选择是非常 nontrival 的,如果特征函数的选择与实际的情况差别比较大,是很难学到好的 policy 的,这也是实际中,当问题比较复杂且先验知识比较小时,往往会选择神经网络来作为特征函数,因为神经网络具有可以拟合任何函数的效力(see:为什么神经网络可以拟合任何函数)。当然这种情况下, v ^ ( s , w ) \hat v(s,w) v^(s,w) 就不再能写成 v ^ ( s , w ) = ϕ T ( s ) w \hat v(s,w) = \phi^T(s)w v^(s,w)=ϕT(s)w 这样线性的形式了。
TD 算法的值函数近似形式
首先给出 目标函数
J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] J(w) = E[(v_{\pi}(S) - \hat v(S,w))^2] J(w)=E[(vπ(S)−v^(S,w))2]
由梯度下降:
w k + 1 = w k − α k ∇ w J ( w k ) w_{k+1} = w_k - \alpha_k \nabla_w J(w_k) wk+1=wk−αk∇wJ(wk)
w k + 1 = w k − α k ∇ w J ( w k ) = w k − α k E [ ∇ w ( v π ( S ) − v ^ ( S , w k ) ) 2 ] = w k + 2 α k E [ ( v π ( S ) − v ^ ( S , w k ) ) ∇ w v ^ ( S , w k ) ] \begin{aligned} w_{k+1} &= w_k - \alpha_k \nabla_w J(w_k)\\ &= w_k - \alpha_k E[\nabla_w(v_{\pi}(S) - \hat v(S,w_k))^2]\\ &= w_k + 2\alpha_k E[(v_{\pi}(S) - \hat v(S,w_k))\nabla_w \hat v(S,w_k)]\\ \end{aligned} wk+1=wk−αk∇wJ(wk)=wk−αkE[∇w(vπ(S)−v^(S,wk))2]=wk+2αkE[(vπ(S)−v^(S,wk))∇wv^(S,wk)]
用 SGD 算法,则有:
w t + 1 = w t + α t ( v π ( s t ) − v ^ ( s t , w t ) ) ∇ w v ^ ( s t , w t ) w_{t+1} = w_t + \alpha_t (v_{\pi}(s_t) - \hat v(s_t,w_t))\nabla_w \hat v(s_t,w_t) wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)
其中 α t \alpha_t αt 等于上面的 2 α k 2\alpha_k 2αk。但这里有一个问题, v π v_{\pi} vπ 就是我们要求的,所以它实际是未知的,跟深度学习一样,这里用样本来替代 golden truth v π ( s t ) v_{\pi}(s_t) vπ(st)。与上一章类似,这里根据样本来更新参数也分成两种办法:
-
蒙特卡洛方法:先采一条 episode ( s 0 , r 1 , s 1 , r 2 , . . . ) (s_0, r_1, s_1, r_2,...) (s0,r1,s1,r2,...),记 g t g_t gt 为其中从 s t s_t st 出发的 trajectory 的 disounted return,那么:
w t + 1 = w t + α t ( g t − v ^ ( s t , w t ) ) ∇ w v ^ ( s t , w t ) w_{t+1} = w_t + \alpha_t ( g_t - \hat v(s_t,w_t))\nabla_w \hat v(s_t,w_t) wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt) -
TD 方法:每拿到一个样本 ( s t , r t , s t + 1 , r t + 1 ) (s_t, r_t, s_{t+1}, r_{t+1}) (st,rt,st+1,rt+1),TD target 为: v ˉ t = r t + 1 + γ v t ( s t + 1 ) \bar{v}_t = r_{t+1} + \gamma v_t(s_{t+1}) vˉt=rt+1+γvt(st+1),这里就用 v ˉ t \bar{v}_t vˉt 来近似 v π ( s t ) v_{\pi}(s_t) vπ(st), 迭代式变成:
w t + 1 = w t + α t ( r t + 1 + γ v ^ t ( s t + 1 ) − v ^ ( s t , w k ) ) ∇ w v ^ ( s t , w k ) w_{t+1} = w_t + \alpha_t ( r_{t+1} + \gamma \hat v_t(s_{t+1}) - \hat v(s_t,w_k))\nabla_w \hat v(s_t,w_k) wt+1=wt+αt(rt+1+γv^t(st+1)−v^(st,wk))∇wv^(st,wk)
NOTE:TD 方法中,用样本 r t + 1 + γ v ^ t ( s t + 1 ) r_{t+1} + \gamma \hat v_t(s_{t+1}) rt+1+γv^t(st+1) 代表 golden truth 会导致一个问题,即模拟的这个 golden truth 永远也不会逃出特征函数 ϕ ( s ) \phi(s) ϕ(s) 的特征空间(因为样本就是当前 Policy 生成的,而当前 Policy 的 state value, 是用我们假设的特征空间中的向量表示的),由于特征空间是根据先验给定的,不一定与实际情况相符 ,所以使用上述 TD 方法,实际求解的是:
J ( w ) = E ( ( v ^ ( w ) − M v π ( w ) ) 2 ) J(w) = E((\hat v(w) - Mv_{\pi}(w))^2) J(w)=E((v^(w)−Mvπ(w))2)
其中 M M M 是将所有向量投影至特征函数展开的特征空间的投影矩阵
这样 当特征空间无法表达真实的 v π v_{\pi} vπ 时,会出现:在样本上训练误差不断减少甚至到0,但与 optimal state value 对比计算的 state value error 却在下降到一定程度后就无法再继续下降了。eg:

Sarsa, Q-learning 的值函数近似形式
Sarsa 与上述 TD 算法的区别在于,它是直接求解 action value 的,回忆 Sarsa 的 tabular 形式:
q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ q t ( s t + 1 , a t + 1 ) ) ] q_{t+1}(s_t,a_t) = q_t(s_t,a_t) - \alpha_t(s_t,a_t) [q_t(s_t,a_t) - (r_{t+1} + \gamma q_t(s_{t+1},a_{t+1}))] qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γqt(st+1,at+1))]
其值函数形式为:
w t + 1 = w t + α t [ r t + 1 + γ q ^ ( s t + 1 , a t + 1 , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1} = w_t + \alpha_t [r_{t+1} + \gamma \hat q(s_{t+1},a_{t+1},w_t) - \hat q(s_t,a_t,w_t)] \nabla_w \hat q(s_t,a_t,w_t) wt+1=wt+αt[rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
算法:

#############################################################################################################
同理,Q-learning 的 tabular 形式:
q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ max a q t ( s t + 1 , a ) ) ] q_{t+1}(s_t,a_t) = q_t(s_t,a_t) - \alpha_t(s_t,a_t) [q_t(s_t,a_t) - (r_{t+1} + \gamma \max_{a} q_t(s_{t+1},a))] qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γamaxqt(st+1,a))]
其值函数形式为:
w t + 1 = w t + α t [ r t + 1 + γ max a q ^ ( s t + 1 , a t + 1 , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1} = w_t + \alpha_t [r_{t+1} + \gamma \max_{a} \hat q(s_{t+1},a_{t+1},w_t) - \hat q(s_t,a_t,w_t)] \nabla_w \hat q(s_t,a_t,w_t) wt+1=wt+αt[rt+1+γamaxq^(st+1,at+1,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
算法:

Deep Q-learning
Deep Q-learning 是将深度学习应用于上述 Q-learning 值函数形式的算法,其中有一些非常经典的实践技巧值得一看。跟 Q-learning 一样,其目标函数:
J ( w ) = E [ ( R + γ max a q ^ ( S ′ , a , w ) − q ^ ( S , A , w ) ) 2 ] J(w) = E[(R + \gamma \max_a \hat q(S',a,w) - \hat q(S,A,w))^2] J(w)=E[(R+γamaxq^(S′,a,w)−q^(S,A,w))2]
实际也相当于在求贝尔曼最优公式,因为上式为0时,也就等价于:
q ( s , a ) = E [ R t + 1 + γ max a q ( S t + 1 , a ) ∣ S t = s , A t = a ] q(s,a) = E[R_{t+1} + \gamma \max_{a} q(S_{t+1},a) |S_t = s, A_t=a ] q(s,a)=E[Rt+1+γamaxq(St+1,a)∣St=s,At=a]
但在对 J ( w ) J(w) J(w) 求导时有一个难点: max a q ^ ( S ′ , a , w ) \max_a \hat q(S',a,w) maxaq^(S′,a,w) 首先不一定是可微的,其次要求这一项的复杂度也非常高(要求对所有可能的 action 都进行求解),最后这一项的梯度往往非常不稳定,不利于模型的收敛。因此 DQN 引入了 target network 的概念:在一定时期内,将 target nerwork 的参数 w T w_T wT 固定住,认为是常值,而只对当前步的 q ^ ( S , A , w ) \hat q(S,A,w) q^(S,A,w) 求导。然后每隔一段时间,再将 main network 中更新到的 w w w 赋给 w T w_T wT 。即
∇ w J ( w ) = − E [ ( R + γ max a q ^ ( S ′ , a , w ) − q ^ ( S , A , w ) ) ∇ w q ^ ( S , A , w ) ] \nabla_w J(w) = - E[(R + \gamma \max_a \hat q(S',a,w) - \hat q(S,A,w)) \nabla_w \hat q(S,A,w)] ∇wJ(w)=−E[(R+γamaxq^(S′,a,w)−q^(S,A,w))∇wq^(S,A,w)]
NOTE:实际使用中,由于深度学习一般是 mini-batch 进行训练的,因此上式的更新实际也是 mini-batch,而不是单个样本。
experience replay
DQN 中还用到了一种叫 experience replay 的采样技术,即对于样本 ( s t , a t , r t + 1 , s t + 1 ) (s_t, a_t, r_{t+1}, s_{t+1}) (st,at,rt+1,st+1),在使用时无需再像之前算法当中那样,根据其在 trajectory 中的顺序来取。而是可以将样本都打散之后,在样本集中随机采样一批来进行迭代更新。这样做的好处是:
- 打破时间相关性:强化学习环境中的连续经验通常是高度相关的,这会导致模型在训练时的高方差和低效率。通过随机采样,经验回放打破了这种时间相关性,使得训练样本更加独立同分布,从而提高了模型的训练稳定性和效率。
- 提高数据利用率:传统的 Q-learning 在每次更新时仅使用最新的经验,可能会浪费之前收集到的宝贵经验。而经验回放可以重用过去的经验,从而提高数据的利用率,使得训练更加高效。(由于 DQN 同时还叠加了值函数近似对样本的高效使用,因此达到同样的效果,其需要的样本量会比普通 Q-learning 小很多,eg:1000 vs 100,000)
DQN 算法:

策略梯度方法(Policy Gradient)
Policy gradient 的想法与 value approximation 类似,只是针对的对象变成了 Policy,将原来 tabular-based 的策略:
π = [ π ( a 1 ∣ s 1 ) π ( a 2 ∣ s 1 ) ⋯ π ( a m ∣ s 1 ) π ( a 1 ∣ s 2 ) π ( a 2 ∣ s 2 ) ⋯ π ( a m ∣ s 2 ) ⋮ ⋮ ⋱ ⋮ π ( a 1 ∣ s n ) π ( a 2 ∣ s n ) ⋯ π ( a m ∣ s n ) ] \pi = \begin{bmatrix} \pi(a_1|s_1) & \pi(a_2|s_1) & \cdots & \pi(a_m|s_1) \\ \pi(a_1|s_2) & \pi(a_2|s_2) & \cdots & \pi(a_m|s_2) \\ \vdots & \vdots & \ddots & \vdots\\ \pi(a_1|s_n) & \pi(a_2|s_n) & \cdots & \pi(a_m|s_n) \end{bmatrix} π= π(a1∣s1)π(a1∣s2)⋮π(a1∣sn)π(a2∣s1)π(a2∣s2)⋮π(a2∣sn)⋯⋯⋱⋯π(am∣s1)π(am∣s2)⋮π(am∣sn)
改成了基于函数的:
π ( a ∣ , s , θ ) = e h ( s , a , θ ) ∑ a ′ e h ( s , a ′ , θ ) \pi(a|,s,\theta) = \frac{e^{h(s,a,\theta)}}{\sum_{a'} e^{h(s,a',\theta)}} π(a∣,s,θ)=∑a′eh(s,a′,θ)eh(s,a,θ)
因为 策略函数通常也是直接用深度学习来表征了,因此在最后一层使用 softmax,即为给定 state 时,每个 action 的概率(softmax 经常用于表征概率分布:因为既能保证概率和为1,又能保证所有的概率值为正)。图例:

Policy Gradient 的目标函数
最优策略的目标函数 J ( θ ) J(\theta) J(θ),依然需要借助最优化 state value / action value 来表达,但不同于之前 valued-based 的算法,这里需要一个统一的标量来表征可以使得所有的 state value / action value 都最大。
目标函数 1
优化 state value,一个自然的想法是 average state value:
v ˉ π = ∑ s d ( s ) v π ( s ) \bar v_{\pi} = \sum_{s} d(s)v_{\pi}(s) vˉπ=s∑d(s)vπ(s)
这里 d ( s ) d(s) d(s) 既 state 的分布,可以分为两种情况:
- d ( s ) d(s) d(s) 与 π \pi π 无关:例如,出现在所有的 state 的概率都相同,即 d ( s i ) = 1 ∣ S ∣ d(s_i) = \frac{1}{|S|} d(si)=∣S∣1
- d ( s ) d(s) d(s) 与 π \pi π 相关:这种情况常用的是 马尔可夫过程的平稳分布
第一章 中提到过强化学习一般都假设满足马尔可夫条件:
P ( s t + 1 ∣ a t + 1 , s t , . . . , a 1 , s 0 ) = P ( s t + 1 ∣ a t + 1 , s t ) P ( r t + 1 ∣ a t + 1 , s t , . . . , a 1 , s 0 ) = P ( r t + 1 ∣ a t + 1 , s t ) \begin{aligned} P(s_{t+1}|a_{t+1},s_t, ..., a_1,s_0) &= P(s_{t+1}|a_{t+1},s_t) \\ P(r_{t+1}|a_{t+1},s_t, ..., a_1,s_0) &= P(r_{t+1}|a_{t+1},s_t) \end{aligned} P(st+1∣at+1,st,...,a1,s0)P(rt+1∣at+1,st,...,a1,s0)=P(st+1∣at+1,st)=P(rt+1∣at+1,st)
而对于一个有穷状态空间的马尔可夫链,记 d k d_k dk 为走了 k k k 步后,state 的概率分布。如果满足该马尔可夫链满足 不可约性,那么它存在唯一的平稳分布 d d d,满足: lim k → ∞ d k = d π \lim_{k \rightarrow \infin} d_k = d_{\pi} k→∞limdk=dπ,即 系统在长时间运行后,各状态之间的转移会趋于稳定,即各状态之间会以固定的概率分布进行转移。 由上式,可得: d π T P π = d π T d^T_{\pi} P_{\pi} = d^T_{\pi} dπTPπ=dπT
其中 P π P_{\pi} Pπ 是马尔可夫链的转移矩阵, [ P π ] i , j [P_{\pi}]_{i,j} [Pπ]i,j 表示从 agent 从 s i s_i si 移动到 s j s_j sj 的概率。
- 不可约性:即对所有的 state, s j s_j sj 和 s j s_j sj ,总存在一个有限的 k,使得 k 步后可以从 s i s_i si 走到 s j s_j sj,即: [ P π k ] i , j > 0 [P_{\pi}^k]_{i,j} > 0 [Pπk]i,j>0
\quad
不可约性要求 policy 是探索性的,因为贪婪策略无法保证从一个 state 出发,可以在有限步内到达任意另一个 state;并且要避免出现"循环"的情况,否则上述 k → ∞ k \rightarrow \infin k→∞
这里 v ˉ π = ∑ s d ( s ) v π ( s ) \bar v_{\pi} = \sum_{s} d(s)v_{\pi}(s) vˉπ=∑sd(s)vπ(s) 中 d ( s ) d(s) d(s) 采用平稳分布的原因也是:在进入平稳运行后, d ( s i ) d(s_i) d(si) 更大的 state,表明有更大的概率走到这个位置,那么在计算 v ˉ π \bar v_{\pi} vˉπ 时,自然应该多给这个 state 一些权重。
等价表达式
除了上述表示, v ˉ π \bar v_{\pi} vˉπ 还有一些等价的表示方法:
- v ˉ π = ∑ s d ( s ) v π ( s ) = ∑ s d ( s ) E [ R 1 + γ R 2 + γ 2 R 3 + . . . ∣ S 0 = s ] = ∑ s d ( s ) E [ ∑ t = 0 ∞ γ t R t + 1 ∣ S 0 = s ] = E [ ∑ t = 0 ∞ γ t R t + 1 ] \begin{aligned} \bar v_{\pi} &= \sum_{s} d(s)v_{\pi}(s)\\ &= \sum_{s} d(s) E[R_{1} + \gamma R_{2} + \gamma^2 R_{3} + ... | S_0 = s]\\ &= \sum_{s} d(s) E[ \sum_{t=0}^{\infin} \gamma^t R_{t+1} | S_0 = s]\\ &= E[ \sum_{t=0}^{\infin} \gamma^t R_{t+1}] \end{aligned} vˉπ=s∑d(s)vπ(s)=s∑d(s)E[R1+γR2+γ2R3+...∣S0=s]=s∑d(s)E[t=0∑∞γtRt+1∣S0=s]=E[t=0∑∞γtRt+1]
- v ˉ π = d T v π \bar v_{\pi} = d^T v_{\pi} vˉπ=dTvπ 其中
v π = [ ⋯ , v π ( s ) , ⋯ ] T ∈ R ∣ S ∣ d = [ ⋯ , d ( s ) , ⋯ ] T ∈ R ∣ S ∣ \begin{aligned} v_{\pi} &= [\cdots, v_{\pi}(s), \cdots]^T \in \mathbb{R}^{|S|}\\ d &= [\cdots, d(s), \cdots]^T \in \mathbb{R}^{|S|} \end{aligned} vπd=[⋯,vπ(s),⋯]T∈R∣S∣=[⋯,d(s),⋯]T∈R∣S∣
目标函数 2
另一个目标函数是 average one-step reward 为基础:
r ˉ π = ∑ s d ( s ) r π ( s ) \bar r_{\pi} = \sum_{s} d(s)r_{\pi}(s) rˉπ=s∑d(s)rπ(s)
其中 d ( s ) d(s) d(s) 与上面相同,而 r π ( s ) = ∑ a π ( a ∣ s , θ ) r ( s , a ) = E A ∼ π ( s , θ ) [ r ( s , A ) ∣ s ] r_{\pi}(s) = \sum_a \pi(a|s,\theta) r(s,a) = E_{A \sim \pi(s,\theta)}[r(s,A)|s] rπ(s)=a∑π(a∣s,θ)r(s,a)=EA∼π(s,θ)[r(s,A)∣s]
即 state s 所有可能的 action 的期望 reward
等价形式
r ˉ π \bar r_{\pi} rˉπ 有一些更常见的等价形式:
-
r ˉ π = lim n → ∞ 1 n E [ ∑ t = 0 n − 1 R t + 1 ] \bar r_{\pi} = \lim_{n \rightarrow \infin} \frac{1}{n} E[\sum_{t=0}^{n-1} R_{t+1}] rˉπ=n→∞limn1E[t=0∑n−1Rt+1]
Proof: 由 Cesaro mean 定理:Cesaro mean 定理
如果 { a k } n = 1 ∞ \{a_k\}_{n=1}^{\infin} {ak}n=1∞ 收敛且满足 lim k → ∞ a k = a ∗ \lim_{k \rightarrow \infin} a_k = a^* k→∞limak=a∗
那么 { 1 n ∑ k = 1 n a k } n = 1 ∞ \{\frac{1}{n} \sum_{k=1}^n a_k\}_{n=1}^{\infin} {n1∑k=1nak}n=1∞ 也收敛,且 lim n → ∞ 1 n ∑ k = 1 n a k = a ∗ \lim_{n \rightarrow \infin} \frac{1}{n} \sum_{k=1}^n a_k = a^* n→∞limn1k=1∑nak=a∗因此 lim n → ∞ 1 n E [ ∑ t = 0 n − 1 R t + 1 ∣ S 0 = s 0 ] = lim t → ∞ E [ R t + 1 ∣ S 0 = s 0 ] = lim t → ∞ ∑ s E [ R t + 1 ∣ S t = s ] P ( t ) ( s ∣ s 0 ) ( P ( t ) ( s ∣ s 0 ) 指从 s 0 出发 t 步后走到 s 的概率 ) = ∑ s r π ( s ) d ( s ) ( 由于 lim t → ∞ P ( t ) ( s ∣ s 0 ) = d ( s ) ) = r ˉ π \begin{aligned} \lim_{n \rightarrow \infin} \frac{1}{n} E[\sum_{t=0}^{n-1} R_{t+1}|S_0=s_0] &= \lim_{t \rightarrow \infin} E[R_{t+1}|S_0=s_0]\\ &= \lim_{t \rightarrow \infin} \sum_{s}E[R_{t+1}|S_t=s] P^{(t)}(s|s_0) \quad (P^{(t)}(s|s_0) 指从 s_0 出发t步后走到 s 的概率)\\ &= \sum_{s} r_{\pi}(s) d(s) \quad (由于 \lim_{t \rightarrow \infin} P^{(t)}(s|s_0) = d(s))\\ &= \bar r_{\pi} \end{aligned} n→∞limn1E[t=0∑n−1Rt+1∣S0=s0]=t→∞limE[Rt+1∣S0=s0]=t→∞lims∑E[Rt+1∣St=s]P(t)(s∣s0)(P(t)(s∣s0)指从s0出发t步后走到s的概率)=s∑rπ(s)d(s)(由于t→∞limP(t)(s∣s0)=d(s))=rˉπ
-
r ˉ π = d T r π \bar r_{\pi} = d^T r_{\pi} rˉπ=dTrπ
其中
r π = [ ⋯ , r π ( s ) , ⋯ ] T ∈ R ∣ S ∣ d = [ ⋯ , d ( s ) , ⋯ ] T ∈ R ∣ S ∣ \begin{aligned} r_{\pi} &= [\cdots, r_{\pi}(s), \cdots]^T \in \mathbb{R}^{|S|}\\ d &= [\cdots, d(s), \cdots]^T \in \mathbb{R}^{|S|} \end{aligned} rπd=[⋯,rπ(s),⋯]T∈R∣S∣=[⋯,d(s),⋯]T∈R∣S∣
综上:

两种目标函数的同一性
可证: r ˉ π = ( 1 − γ ) v ˉ π \bar r_{\pi} = (1-\gamma)\bar v_{\pi} rˉπ=(1−γ)vˉπ
Proof:由贝尔曼公式 v π = r π + γ P π v π v_{\pi} = r_{\pi} + \gamma P_{\pi} v_{\pi} vπ=rπ+γPπvπ
因此
d π T v π = d π T r π + γ d π T P π v π ⇒ v ˉ π = r ˉ π + γ d π T v π ( 由平稳分布的性质: d π T P π = d π T ) v ˉ π = r ˉ π + γ v ˉ π \begin{aligned} d_{\pi}^T v_{\pi} &= d_{\pi}^T r_{\pi} + \gamma d_{\pi}^T P_{\pi} v_{\pi}\\ \Rightarrow \qquad \bar v_{\pi} &= \bar r_{\pi} + \gamma d_{\pi}^T v_{\pi} \qquad (由平稳分布的性质:d^T_{\pi} P_{\pi} = d^T_{\pi})\\ \bar v_{\pi} &= \bar r_{\pi} + \gamma \bar v_{\pi} \end{aligned} dπTvπ⇒vˉπvˉπ=dπTrπ+γdπTPπvπ=rˉπ+γdπTvπ(由平稳分布的性质:dπTPπ=dπT)=rˉπ+γvˉπ
因此使得 v ˉ π \bar v_{\pi} vˉπ 最大的 θ \theta θ 同样也会使得 r ˉ π \bar r_{\pi} rˉπ 最大,在最优化问题中,这两个统计量等价。
Policy Gradient 目标函数的梯度
首先给出各种目标函数梯度的统一形式,后面再依次证明梯度确实符合这个形式:
Policy Gradient 目标函数梯度的统一形式
∇ θ J ( θ ) = ∑ s η ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) \nabla_{\theta} J(\theta) = \sum_s \eta(s) \sum_a \nabla_{\theta} \pi(a|s,\theta) q_{\pi}(s,a) ∇θJ(θ)=s∑η(s)a∑∇θπ(a∣s,θ)qπ(s,a)
上式的一个等价形式: ∇ θ J ( θ ) = E S ∼ η , A ∼ π ( S , θ ) [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \nabla_{\theta} J(\theta) = E _{S \sim \eta, A \sim \pi(S,\theta)} [\nabla_{\theta} \ln \pi(A|S,\theta) q_{\pi}(S,A)] ∇θJ(θ)=ES∼η,A∼π(S,θ)[∇θlnπ(A∣S,θ)qπ(S,A)]
Proof:
∇ θ J ( θ ) = ∑ s η ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) = E S ∼ η [ ∑ a ∇ θ π ( a ∣ S , θ ) q π ( S , a ) ] = E S ∼ η [ ∑ a π ( a ∣ S , θ ) ∇ θ ln π ( a ∣ S , θ ) q π ( S , a ) ] ( 因为 ∇ θ ln π ( a ∣ S , θ ) = ∇ θ π ( a ∣ S , θ ) π ( a ∣ S , θ ) ) = E S ∼ η , A ∼ π ( S , θ ) [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \begin{aligned} \nabla_{\theta} J(\theta) &= \sum_s \eta(s) \sum_a \nabla_{\theta} \pi(a|s,\theta) q_{\pi}(s,a)\\ &= E _{S \sim \eta} [\sum_a \nabla_{\theta} \pi(a|S,\theta) q_{\pi}(S,a)]\\ &= E _{S \sim \eta}[\sum_a \pi(a|S,\theta) \nabla_{\theta} \ln \pi(a|S,\theta) q_{\pi}(S,a)] \qquad (因为 \nabla_{\theta} \ln \pi(a|S,\theta) = \frac{\nabla_{\theta} \pi(a|S,\theta)}{\pi(a|S,\theta)})\\ &= E _{S \sim \eta, A \sim \pi(S,\theta)} [\nabla_{\theta} \ln \pi(A|S,\theta) q_{\pi}(S,A)] \end{aligned} ∇θJ(θ)=s∑η(s)a∑∇θπ(a∣s,θ)qπ(s,a)=ES∼η[a∑∇θπ(a∣S,θ)qπ(S,a)]=ES∼η[a∑π(a∣S,θ)∇θlnπ(a∣S,θ)qπ(S,a)](因为∇θlnπ(a∣S,θ)=π(a∣S,θ)∇θπ(a∣S,θ))=ES∼η,A∼π(S,θ)[∇θlnπ(A∣S,θ)qπ(S,A)]
discounted case 情形下的目标函数梯度
当 γ ∈ ( 0 , 1 ) \gamma \in (0,1) γ∈(0,1) 时,由于 r ˉ π = ( 1 − γ ) v ˉ π \bar r_{\pi} = (1-\gamma)\bar v_{\pi} rˉπ=(1−γ)vˉπ,因此可以只求 ∇ θ v ˉ π \nabla_{\theta} \bar v_{\pi} ∇θvˉπ ,这里首先给出 v π v_{\pi} vπ 的梯度: ∇ θ v π ( s ) = ∑ s ′ ∑ k = 0 ∞ γ k [ P π k ] s s ′ ∑ a ∇ θ π ( a ∣ s ′ , θ ) q π ( s ′ , a ) \nabla_{\theta} v_{\pi}(s) = \sum_{s'} \sum_{k=0}^{\infin} \gamma^k [P_{\pi}^k]_{ss'} \sum_a \nabla_{\theta} \pi(a|s',\theta) q_{\pi}(s',a) ∇θvπ(s)=s′∑k=0∑∞γk[Pπk]ss′a∑∇θπ(a∣s′,θ)qπ(s′,a)
Proof:
∇ θ v π ( s ) = ∇ θ [ ∑ a π ( a ∣ s , θ ) q π ( s , a ) ] = ∑ a [ ∇ θ π ( a ∣ s , θ ) q π ( s , a ) + π ( a ∣ s , θ ) ∇ θ q π ( s , a ) ] \begin{aligned} \nabla_{\theta} v_{\pi}(s) &= \nabla_{\theta}[\sum_a \pi(a|s,\theta) q_{\pi}(s,a)]\\ &= \sum_a [\nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) + \pi(a|s,\theta) \nabla_{\theta}q_{\pi}(s,a)]\\ \end{aligned} ∇θvπ(s)=∇θ[a∑π(a∣s,θ)qπ(s,a)]=a∑[∇θπ(a∣s,θ)qπ(s,a)+π(a∣s,θ)∇θqπ(s,a)]
由于
∇ θ q π ( s , a ) = ∇ θ [ ∑ r P ( r ∣ s , a ) r + γ ∑ s ′ P ( s ′ ∣ s , a ) v π ( s ′ ) ] = 0 + γ ∑ s ′ P ( s ′ ∣ s , a ) ∇ θ v π ( s ′ ) \begin{aligned} \nabla_{\theta} q_{\pi}(s,a) &= \nabla_{\theta} [\sum_r P(r|s,a)r + \gamma \sum_{s'}P(s'|s,a)v_{\pi}(s')]\\ &= 0 + \gamma \sum_{s'}P(s'|s,a) \nabla_{\theta}v_{\pi}(s') \end{aligned} ∇θqπ(s,a)=∇θ[r∑P(r∣s,a)r+γs′∑P(s′∣s,a)vπ(s′)]=0+γs′∑P(s′∣s,a)∇θvπ(s′)
因此:
∇ θ v π ( s ) = ∑ a [ ∇ θ π ( a ∣ s , θ ) q π ( s , a ) + π ( a ∣ s , θ ) γ ∑ s ′ P ( s ′ ∣ s , a ) ∇ θ v π ( s ′ ) ] = ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s ) ∇ θ v π ( s ′ ) = ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) + γ ∑ s ′ [ P π ] s s ′ ∇ θ v π ( s ′ ) = u ( s ) + γ ∑ s ′ ( P π ⊗ I m ) ∇ θ v π ( s ′ ) ( 记 u ( s ) = ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) ) \begin{aligned} \nabla_{\theta} v_{\pi}(s) &= \sum_a [\nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) + \pi(a|s,\theta) \gamma \sum_{s'}P(s'|s,a) \nabla_{\theta}v_{\pi}(s')]\\ &= \sum_a \nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) + \gamma \sum_{s'}P(s'|s) \nabla_{\theta}v_{\pi}(s')\\ &= \sum_a \nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) + \gamma \sum_{s'} [P_{\pi}]_{ss'} \nabla_{\theta}v_{\pi}(s')\\ &= u(s) + \gamma \sum_{s'} (P_{\pi} \otimes I_m) \nabla_{\theta}v_{\pi}(s') \qquad (记 u(s) = \sum_a \nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a)) \end{aligned} ∇θvπ(s)=a∑[∇θπ(a∣s,θ)qπ(s,a)+π(a∣s,θ)γs′∑P(s′∣s,a)∇θvπ(s′)]=a∑∇θπ(a∣s,θ)qπ(s,a)+γs′∑P(s′∣s)∇θvπ(s′)=a∑∇θπ(a∣s,θ)qπ(s,a)+γs′∑[Pπ]ss′∇θvπ(s′)=u(s)+γs′∑(Pπ⊗Im)∇θvπ(s′)(记u(s)=a∑∇θπ(a∣s,θ)qπ(s,a))
上式可以求解:
∇ θ v π ( s ) = ∑ s ′ ( I n m − γ P π ⊗ I m ) − 1 u ( s ′ ) = ∑ s ′ ( I n ⊗ I m − γ P π ⊗ I m ) − 1 u ( s ′ ) = ∑ s ′ [ ( I n − γ P π ) − 1 ⊗ I m ] u ( s ′ ) = ∑ s ′ [ ( I n − γ P π ) − 1 ] s s ′ u ( s ′ ) = ∑ s ′ [ ( I n − γ P π ) − 1 ] s s ′ ∑ a ∇ θ π ( a ∣ s ′ , θ ) q π ( s ′ , a ) = ∑ s ′ [ I + γ P π + γ 2 P π 2 + ⋯ ] s s ′ ∑ a ∇ θ π ( a ∣ s ′ , θ ) q π ( s ′ , a ) = ∑ s ′ ∑ k = 0 ∞ γ k [ P π k ] s s ′ ∑ a ∇ θ π ( a ∣ s ′ , θ ) q π ( s ′ , a ) \begin{aligned} \nabla_{\theta} v_{\pi}(s) &= \sum_{s'}(I_{nm} - \gamma P_{\pi} \otimes I_m)^{-1} u(s')\\ &= \sum_{s'}(I_n \otimes I_m - \gamma P_{\pi} \otimes I_m)^{-1} u(s')\\ &= \sum_{s'}[(I_n - \gamma P_{\pi})^{-1} \otimes I_m ] u(s')\\ &= \sum_{s'}[(I_n - \gamma P_{\pi})^{-1}]_{ss'} u(s')\\ &= \sum_{s'}[(I_n - \gamma P_{\pi})^{-1}]_{ss'} \sum_a \nabla_{\theta}\pi(a|s',\theta) q_{\pi}(s',a)\\ &= \sum_{s'} [I + \gamma P_{\pi} + \gamma^2 P_{\pi}^2 + \cdots]_{ss'} \sum_a \nabla_{\theta}\pi(a|s',\theta) q_{\pi}(s',a)\\ &= \sum_{s'} \sum_{k=0}^{\infin} \gamma^k [P_{\pi}^k]_{ss'} \sum_a \nabla_{\theta} \pi(a|s',\theta) q_{\pi}(s',a) \end{aligned} ∇θvπ(s)=s′∑(Inm−γPπ⊗Im)−1u(s′)=s′∑(In⊗Im−γPπ⊗Im)−1u(s′)=s′∑[(In−γPπ)−1⊗Im]u(s′)=s′∑[(In−γPπ)−1]ss′u(s′)=s′∑[(In−γPπ)−1]ss′a∑∇θπ(a∣s′,θ)qπ(s′,a)=s′∑[I+γPπ+γ2Pπ2+⋯]ss′a∑∇θπ(a∣s′,θ)qπ(s′,a)=s′∑k=0∑∞γk[Pπk]ss′a∑∇θπ(a∣s′,θ)qπ(s′,a)
下面求解 v ˉ π \bar v_{\pi} vˉπ 的梯度 ,先给结论:
当 γ \gamma γ 靠近 1 时,
∇ θ r ˉ π ( s ) = ( 1 − γ ) ∇ θ v ˉ π ( s ) ≈ ∑ s d π ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) = E S ∼ d π , A ∼ π ( S , θ ) [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \begin{aligned} \nabla_{\theta} \bar r_{\pi}(s) &= (1-\gamma)\nabla_{\theta} \bar v_{\pi}(s) \\ &\approx \sum_s d_{\pi}(s) \sum_a \nabla_{\theta} \pi(a|s,\theta) q_{\pi}(s,a)\\ &= E_{S \sim d_{\pi}, A \sim \pi(S,\theta)} [\nabla_{\theta} \ln \pi(A|S,\theta) q_{\pi}(S,A)] \end{aligned} ∇θrˉπ(s)=(1−γ)∇θvˉπ(s)≈s∑dπ(s)a∑∇θπ(a∣s,θ)qπ(s,a)=ES∼dπ,A∼π(S,θ)[∇θlnπ(A∣S,θ)qπ(S,A)]
Proof:
∇ θ v ˉ π ( s ) = ∇ θ [ ∑ s d π ( s ) v π ( s ) ] = ∑ s ∇ θ d π ( s ) v π ( s ) + ∑ s d π ( s ) ∇ θ v π ( s ) (1) \begin{aligned} \nabla_{\theta} \bar v_{\pi}(s) &= \nabla_{\theta} [\sum_s d_{\pi}(s)v_{\pi}(s)]\\ &= \sum_s \nabla_{\theta}d_{\pi}(s)v_{\pi}(s) + \sum_s d_{\pi}(s) \nabla_{\theta} v_{\pi}(s) \end{aligned} \tag{1} ∇θvˉπ(s)=∇θ[s∑dπ(s)vπ(s)]=s∑∇θdπ(s)vπ(s)+s∑dπ(s)∇θvπ(s)(1)
其中
∑ s d π ( s ) ∇ θ v π ( s ) = ( d π T ⊗ I m ) v π ( s ) = ( d π T ⊗ I m ) [ ( I n − γ P π ) − 1 ⊗ I m ] u ( s ) = [ d π T ( I n − γ P π ) − 1 ] ⊗ I m u ( s ) = 1 1 − γ d π T ⊗ I m u ( s ) ( 因为 d π T ( I n − γ P π ) = d π T − γ d π T ) = 1 1 − γ ∑ s d π ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) \begin{aligned} \sum_s d_{\pi}(s) \nabla_{\theta} v_{\pi}(s) &= (d_{\pi}^T \otimes I_m) v_{\pi}(s) \\ &= (d_{\pi}^T \otimes I_m) [(I_n - \gamma P_{\pi})^{-1} \otimes I_m] u(s)\\ &= [d_{\pi}^T (I_n - \gamma P_{\pi})^{-1}] \otimes I_m u(s)\\ &= \frac{1}{1-\gamma} d_{\pi}^T \otimes I_m u(s) \qquad (因为 d_{\pi}^T(I_n - \gamma P_{\pi}) = d_{\pi}^T - \gamma d_{\pi}^T) \\ &= \frac{1}{1-\gamma} \sum_s d_{\pi}(s) \sum_a \nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) \end{aligned} s∑dπ(s)∇θvπ(s)=(dπT⊗Im)vπ(s)=(dπT⊗Im)[(In−γPπ)−1⊗Im]u(s)=[dπT(In−γPπ)−1]⊗Imu(s)=1−γ1dπT⊗Imu(s)(因为dπT(In−γPπ)=dπT−γdπT)=1−γ1s∑dπ(s)a∑∇θπ(a∣s,θ)qπ(s,a)
当 γ → 1 \gamma \rightarrow 1 γ→1 时, ( 1 ) (1) (1) 式中第二项占主导,第一项相对第二项可以忽略不计,因此:
∇ θ r ˉ π ( s ) = ( 1 − γ ) ∇ θ v ˉ π ( s ) ≈ ∑ s d π ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) \begin{aligned} \nabla_{\theta} \bar r_{\pi}(s) &= (1-\gamma)\nabla_{\theta} \bar v_{\pi}(s) \\ &\approx \sum_s d_{\pi}(s) \sum_a \nabla_{\theta}\pi(a|s,\theta) q_{\pi}(s,a) \end{aligned} ∇θrˉπ(s)=(1−γ)∇θvˉπ(s)≈s∑dπ(s)a∑∇θπ(a∣s,θ)qπ(s,a)
undiscounted case 情形下的目标函数梯度
此时 γ = 1 \gamma =1 γ=1,可以证明,此时上述约等号变成等号,即:
∇ θ r ˉ π ( s ) = ( 1 − γ ) ∇ θ v ˉ π ( s ) = ∑ s d π ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) = E S ∼ d π , A ∼ π ( S , θ ) [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \begin{aligned} \nabla_{\theta} \bar r_{\pi}(s) &= (1-\gamma)\nabla_{\theta} \bar v_{\pi}(s) \\ &= \sum_s d_{\pi}(s) \sum_a \nabla_{\theta} \pi(a|s,\theta) q_{\pi}(s,a)\\ &= E_{S \sim d_{\pi}, A \sim \pi(S,\theta)} [\nabla_{\theta} \ln \pi(A|S,\theta) q_{\pi}(S,A)] \end{aligned} ∇θrˉπ(s)=(1−γ)∇θvˉπ(s)=s∑dπ(s)a∑∇θπ(a∣s,θ)qπ(s,a)=ES∼dπ,A∼π(S,θ)[∇θlnπ(A∣S,θ)qπ(S,A)]
详细推导见 强化学习的数学原理
蒙特卡洛 policy gradient ( REINFORCE 算法)
根据上述推导,Policy gradient 的迭代式是:
θ t + 1 = θ t + α ∇ θ J ( θ t ) = θ t + α ∇ θ E [ ∇ θ ln π ( A ∣ S , θ t ) q π ( S , A ) ] \begin{aligned} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta} J(\theta_t)\\ &= \theta_t + \alpha \nabla_{\theta} E[\nabla_{\theta} \ln \pi(A|S,\theta_t) q_{\pi}(S,A)] \end{aligned} θt+1=θt+α∇θJ(θt)=θt+α∇θE[∇θlnπ(A∣S,θt)qπ(S,A)]
由于真实的 q π ( S , A ) q_{\pi}(S,A) qπ(S,A) 未知,所以如果是t哦那个给蒙特卡洛方法用样本来模拟,则称为 REINFORCE 算法:
θ t + 1 = θ t + α ∇ θ ln π ( a t ∣ s t , θ t ) q π ( s t , a t ) = θ t + α ∇ θ π ( a t ∣ s t , θ t ) π ( a t ∣ s t , θ t ) q π ( s t , a t ) = θ t + α q π ( s t , a t ) π ( a t ∣ s t , θ t ) ∇ θ π ( a t ∣ s t , θ t ) = θ t + α β t ∇ θ π ( a t ∣ s t , θ t ) ( 这里记 β t = q π ( s t , a t ) π ( a t ∣ s t , θ t ) ) \begin{aligned} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta} \ln \pi(a_t|s_t,\theta_t) q_{\pi}(s_t,a_t)\\ &= \theta_t + \alpha \frac{\nabla_{\theta}\pi(a_t|s_t,\theta_t)}{\pi(a_t|s_t,\theta_t)} q_{\pi}(s_t,a_t)\\ &= \theta_t + \alpha \frac{q_{\pi}(s_t,a_t)}{\pi(a_t|s_t,\theta_t)} \nabla_{\theta}\pi(a_t|s_t,\theta_t)\\ &= \theta_t + \alpha \beta_t \nabla_{\theta}\pi(a_t|s_t,\theta_t) \qquad (这里记 \beta_t = \frac{q_{\pi}(s_t,a_t)}{\pi(a_t|s_t,\theta_t)}) \end{aligned} θt+1=θt+α∇θlnπ(at∣st,θt)qπ(st,at)=θt+απ(at∣st,θt)∇θπ(at∣st,θt)qπ(st,at)=θt+απ(at∣st,θt)qπ(st,at)∇θπ(at∣st,θt)=θt+αβt∇θπ(at∣st,θt)(这里记βt=π(at∣st,θt)qπ(st,at))
上述迭代式有两个结论:
- 当 β t ≥ 0 \beta_t \geq 0 βt≥0 时,上式是梯度上升,因此 π ( a t ∣ s t , θ t + 1 ) ≥ π ( a t ∣ s t , θ t ) \pi(a_t|s_t,\theta_{t+1}) \geq \pi(a_t|s_t,\theta_t) π(at∣st,θt+1)≥π(at∣st,θt),即新的 policy 会更倾向于选择 a t a_t at;而当 β t < 0 \beta_t < 0 βt<0 时,上式是梯度下降, π ( a t ∣ s t , θ t + 1 ) < π ( a t ∣ s t , θ t ) \pi(a_t|s_t,\theta_{t+1}) < \pi(a_t|s_t,\theta_t) π(at∣st,θt+1)<π(at∣st,θt),因此新的 policy 会更不倾向于选择 a t a_t at
- 再分析 β t \beta_t βt 的构成: β t = q π ( s t , a t ) π ( a t ∣ s t , θ t ) \beta_t = \frac{q_{\pi}(s_t,a_t)}{\pi(a_t|s_t,\theta_t)} βt=π(at∣st,θt)qπ(st,at) 首先 β t \beta_t βt 与 q π ( s t , a t ) q_{\pi}(s_t,a_t) qπ(st,at) 成正比,因此 q π ( s t , a t ) q_{\pi}(s_t,a_t) qπ(st,at) 越大,即样本中 a t a_t at 的 action value 越大, β t \beta_t βt 越大(因此新的 policy 会更倾向于选择 a t a_t at,make sense)。但另一方面, β t \beta_t βt 与 π ( a t ∣ s t , θ t ) \pi(a_t|s_t,\theta_t) π(at∣st,θt) 成反比,即当前策略选择 a t a_t at 的概率越大,那么更新后的策略反而会减少选择 a t a_t at 的概率,这是由于 Policy gradient 方法都是 on-policy 的(由于样本中的 a t a_t at 需依赖当前策略 π \pi π),这样的话,可以保持策略的 exploration。
如何采样
理论上来说,应该是 S ∼ d π , A ∼ π ( A ∣ S , θ ) S \sim d_{\pi}, A\sim \pi(A|S,\theta) S∼dπ,A∼π(A∣S,θ),其中 d π d_{\pi} dπ 是 π \pi π 的平稳分布(即运行很多步后的样本), π ( A ∣ S , θ ) \pi(A|S,\theta) π(A∣S,θ) 是当前的策略。但实际使用中,由于标准的做法效率比较低,实际是根据当前的 π ( θ ) \pi(\theta) π(θ) 先采一个 episode,再利用这个 episode 中的数据更新一波:

Reference:
1.强化学习的数学原理
相关文章:

【强化学习的数学原理】课程笔记--5(值函数近似,策略梯度方法)
目录 值函数近似一个例子TD 算法的值函数近似形式Sarsa, Q-learning 的值函数近似形式Deep Q-learningexperience replay 策略梯度方法(Policy Gradient)Policy Gradient 的目标函数目标函数 1目标函数 2两种目标函数的同一性 Policy Gradient 目标函数的…...

前端Long类型精度丢失:后端处理策略
文章目录 精度丢失的具体原因解决方法1. 使用 JsonSerialize 和 ToStringSerializer2. 使用 JsonFormat 注解3. 全局配置解决方案 结论 开发商城管理系统的品牌管理界面时,发现一个问题,接口返回品牌Id和页面展示的品牌Id不一致,如接口返回的…...

C++ | Leetcode C++题解之第300题最长递增子序列
题目: 题解: class Solution { public:int lengthOfLIS(vector<int>& nums) {int len 1, n (int)nums.size();if (n 0) {return 0;}vector<int> d(n 1, 0);d[len] nums[0];for (int i 1; i < n; i) {if (nums[i] > d[len])…...
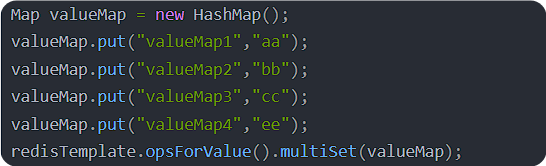
springboo 整合 redis
springBoot 整合 redis starter启动依赖。—包含自动装配类—完成相应的装配功能。 引入依赖 <!--引入了redis整合springboot 的依赖--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis&…...

dpdk编译安装以及接收udp报文(基于ubuntu)
目录 1、编译 2、设置运行环境 3、使用dpdk接收udp报文 3.1、设置发送端arp信息 3.2、测试 3.3、代码 4、其他 1、编译 代码下载: DPDK 下载版本:DPDK 19.08.2 export RTE_SDK/root/dpdk-stable-19.08.2/ export RTE_TARGETx86_64-native-li…...

【计算机网络】OSPF单区域实验
一:实验目的 1:掌握在路由器上配置OSPF单区域。 2:学习OSPF协议的原理,及其网络拓扑结构改变后的变化。 二:实验仪器设备及软件 硬件:RCMS交换机、网线、内网网卡接口、Windows 2019操作系统的计算机等。…...

Java聚合快递小程序对接云洋系统程序app源码
一场物流效率的革命 引言:物流新时代的序章 在数字化浪潮席卷各行各业的今天,物流行业也迎来了前所未有的变革。为了进一步提升物流效率,优化用户体验,聚合快递系统与云洋系统小程序的对接成为了行业内外关注的焦点。这一创新…...

【React】详解组件通信:从基础到进阶的全面指南
文章目录 一、父组件向子组件传递数据1. 基本概念2. 示例代码3. 详解定义子组件 Son定义父组件 App导出父组件 App数据流props 的内容 二、子组件向父组件传递数据1. 基本概念2. 示例代码3. 详解引入React库和useState钩子定义子组件 Son定义父组件 App导出父组件 App数据流 三…...

【vluhub】zabbix漏洞
介绍: zabbix是对服务器资源状态例如、内存空间、CPU、程序运行状态进行检测、设置预警值、短信设置等功能等一款开源工具。配置不当存在未授权,SQL注入漏洞 弱口令 nameadmin&passwordzabbix nameguest&password POST /index.php HTTP/1.1 Host: 192.1…...

openGauss触发器详解
openGauss 是一款开源关系型数据库管理系统,广泛应用于企业级应用中。随着数据量的增长和业务逻辑的复杂化,数据库管理和操作的自动化需求越来越高。触发器(Triggers)作为数据库中重要的编程工具,能够极大地简化复杂操…...

抄作业-跟着《React通关秘籍》捣鼓React-playground-上集
文章目录 前言1. 搭建react 开发环境2、react hooks 知识3. 目标:跟着小册实现 react-playground3.1 整体布局初始化项目使用Alloment 来实现左右分屏的拖拉功能 3.2 代码编辑器Monaco Editor 3.3 实现了多文件的切换用 useContext 来共享数据。优化 tab的样式&…...

80后最后的书信 年代
当时11亿人口只有1.8万部固定电话 中国几千年来 鱼传尺素 雁寄鸿书 写信最后要写 亲啓 如有照片,封面要写内有照片,请勿折叠 信的开头应该是 见字如面,展信舒颜 如果拜托别人做事情,最后要写为盼 最后要写 某某草 书未尽…...

软考-软件设计师(4)-计算机网络与安全:OSI七层、子网划分、网络安全控制技术、网络安全协议、网络安全威胁、对称与非对称加密等高频考点
场景 软考-软件设计师-计算机网络与信息安全模块高频考点整理。 以下为高频考点、知识点汇总,不代表该模块所有知识点覆盖,请以官方教程提纲为准。 注: 博客:霸道流氓气质-CSDN博客 实现 知识点 OSI/RM七层模型 注意各层的主要功能,特别是表示层负责数据的加密、压…...

Unity横板动作游戏 -为什么我又开始学习Unity,而不是Godot。
Readme 最近开始学习Unity制作2D动作游戏,由于一些操作第一次接触,为了加深印象,准备写这样一篇同步教程的笔记。 之前也接触过Unity,用 Unity 制作过一个非常简单的小游戏 Flappy Bird,并且魔改成了泰拉瑞亚的版本。…...

什么是NIO
NIO(New Input/Output),也称为Java非阻塞IO,是从Java 1.4版本开始引入的一个新的IO API,旨在提供一种比传统的阻塞IO更高效、更灵活的IO操作方式。 一 NIO用法的详细介绍 NIO支持面向缓冲区的、基于通道的IO操作&…...

PHP switch 替代品 match
match 是 PHP 8 中引入的新特性。在 PHP 8 中,match 用作新的类型安全的替代 switch 语句。它提供了更清晰、更简洁的语法,同时还支持表达式作为条件,可以更轻松地处理复杂的条件逻辑。 在 match 表达式中,每个分支都是一个条件和…...

FastAPI(七十四)实战开发《在线课程学习系统》接口开发-- 删除留言
源码见:"fastapi_study_road-learning_system_online_courses: fastapi框架实战之--在线课程学习系统" 之前文章FastAPI(七十三)实战开发《在线课程学习系统》接口开发-- 回复留言,那么我们这次分享删除留言接口的开发…...

面试重点---快速排序
快排单趟 快速排序是我们面试中的重点,这个知识点也很抽象,需要我们很好的掌握,而且快速排序的代码也是非常重要,需要我们懂了还不行,必须要手撕代码,学的透彻。 在研究快速排序之前,我们首先…...
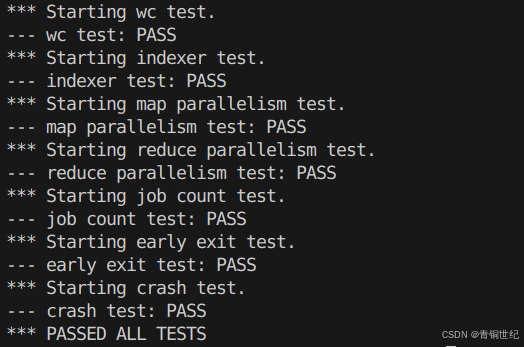
[MIT6.5840]MapReduce
MapReduce Lab 地址 https://pdos.csail.mit.edu/6.824/labs/lab-mr.html 论文地址 https://static.googleusercontent.com/media/research.google.com/zh-CN//archive/mapreduce-osdi04.pdf 工作原理 简单来讲,MapReduce是一种分布式框架,可以用来处理…...

【系统架构设计师】计算机组成与体系结构 ⑯ ( 奇偶校验码 | CRC 循环冗余码 | 海明码 | 模 2 除法 )
文章目录 一、校验码1、校验码由来2、奇偶校验码3、CRC 循环冗余码 ( 重点考点 )4、海明码校验 ( 软考不经常考到 ) 二、CRC 循环冗余码 ( 重点考点 )1、模 2 除法概念2、模 2 除法步骤3、模 2 除法示例4、CRC 循环冗余码示例 15、CRC 循环冗余码示例 2 参考之前的博客 : 【计…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
