Centos 7系统(最小化安装)安装Git 、git-man帮助、补全git命令-详细文章
安装之前由于是最小化安装centos7安装一些开发环境和工具包
文章使用国内阿里源
cd /etc/yum.repos.d/ && mkdir myrepo && mv * myrepo&&ls
curl -O https://mirrors.aliyun.com/repo/epel-7.repo;curl -O https://mirrors.aliyun.com/repo/Centos-7.repo && yum makecache all启用阿里源yum云。
由于是最小化安装的系统没有开发工具、编译器、构建工具、base(基础工具),安装系统环境。
yum -y groupinstall "development tools" "base"
git即便是最小化安装的系统也会默认已安装的。所以需要删除已经安装的git。安装新版本。
使用yum查询是否安装
yum info installed git

删除git
yum -y remove git
Git官网链接

1、获取源代码包的方法-downloads

2、点击Older releases

最新版本是2.45.2版本
git-2.45.2.tar.xg官网下载链接 git-2.45.2.tar.gz官网下载链接
安装git
进入/usr/local/src目录创建git目录,下载git-2.45.2.tar.xg源代码安装包。
cd /usr/local/src/&&mkdir git&&cd git&& wget https://mirrors.edge.kernel.org/pub/software/scm/git/git-2.45.2.tar.xz
进行解压
tar xf git-2.45.2.tar.xz&& cd git-2.45.2
配置git
安装git启用选项配置的一些依赖包,如果直接是./configure --prefix=* ,则不需要安装。
yum -y install openssl-devel libcurl-devel libexpat-devel libpcre2-devel libiconv-devel zlib-devel tcl-devel tk-devel
./configure --prefix=/usr/local/git --with-openssl --with-curl --with-expat --with-libpcre2 --with-iconv --with-zlib --with-tcltk
-
基本选项:
--with-openssl: 开启对OpenSSL的支持是必要的,因为它提供了加密支持,对于HTTPS协议的使用至关重要。--with-curl: 同样,开启CURL支持也是必要的,因为它允许git通过HTTP(S)协议进行操作。--with-expat: 开启Expat支持,它用于支持WebDAV协议,这对于使用HTTP(S)传输非常有用。
-
常规选项:
--with-libpcre2: 如果你的应用需要Perl兼容正则表达式的功能,那么应该启用这项支持。--with-iconv: 如果你的环境需要处理多种字符集转换,那么启用iconv支持是非常有帮助的。
-
高级选项:
--with-zlib: 如果你的系统上已经安装了zlib,那么你可以指定其路径来确保git可以正确地压缩数据。--with-perl和--with-python: 这些选项通常只在你需要使用特定版本的Perl或Python脚本时才需要指定。如果你不需要这些脚本或者你的系统已经默认安装了这些工具,那么通常不需要特别指定。
-
GUI选项:
--with-tcltk: 如果你计划使用git-gui工具,并且你的系统已经安装了Tcl/Tk,那么可以启用这个选项。
-
其他选项:
--with-sane-tool-path: 如果你需要确保git构建过程中使用的工具路径与你的系统配置一致,可以使用这个选项。--with-gitconfig和--with-gitattributes: 如果你需要自定义全局配置文件的位置,可以使用这些选项。--with-pager和--with-editor: 如果你需要指定默认的分页器或编辑器,可以使用这些选项。
make && make install

看到done(完成)代表安装成功了。
git添加环境
vim /etc/profile
export GIT_HOME=/usr/local/git
export PATH=$PATH:$GIT_HOME/bin
此时便可以使用git了,但是命令却不能补全
cat /usr/local/src/git/git-2.45.2/contrib/completion/git-completion.bash >> /root/.bashrc
source /root/.bashrc
下载git的man手册帮助
选择与安装版本对应的版本包

官网下载链接git-manpages-2.45.2.tar.xz 官网下载链接git-manpages-2.45.2.tar.gz
cd /usr/local/src/&& mkdir gitman&&cd gitman&& wget https://mirrors.edge.kernel.org/pub/software/scm/git/git-manpages-2.45.2.tar.xz
tar xf git-manpages-2.45.2.tar.xz
cp man1/* /usr/local/share/man/man1
cp man5/* /usr/local/share/man/man5
cp man7/* /usr/local/share/man/man7
之后便可以使用man手册了。
man git
相关文章:

Centos 7系统(最小化安装)安装Git 、git-man帮助、补全git命令-详细文章
安装之前由于是最小化安装centos7安装一些开发环境和工具包 文章使用国内阿里源 cd /etc/yum.repos.d/ && mkdir myrepo && mv * myrepo&&lscurl -O https://mirrors.aliyun.com/repo/epel-7.repo;curl -O https://mirrors.aliyun.com/repo/Centos-7…...
Golang零基础入门课_20240726 课程笔记
视频课程 最近发现越来越多的公司在用Golang了,所以精心整理了一套视频教程给大家,这个只是其中的第一部,后续还会有很多。 视频已经录制完成,完整目录截图如下: 课程目录 01 第一个Go程序.mp402 定义变量.mp403 …...

杂记-镜像
-i https://pypi.tuna.tsinghua.edu.cn/simple 清华 pip intall 出现 error: subprocess-exited-with-error 错误的解决办法———————————pip install --upgrade pip setuptools57.5.0 ————————————————————————————————————…...

如何将WordPress文章中的外链图片批量导入到本地
在使用采集软件进行内容创作时,很多文章中的图片都是远程链接,这不仅会导致前端加载速度慢,还会在微信小程序和抖音小程序中添加各种域名,造成管理上的麻烦。特别是遇到没有备案的外链,更是让人头疼。因此,…...

primetime如何合并不同modes的libs到一个lib文件
首先,用primetime 抽 timing model 的指令如下。 代码如下(示例): #抽lib时留一些margin, setup -max/hold -min set_extract_model_margin -port [get_ports -filter "!defined(clocks)"] -max 0.1 #抽lib extract_mod…...
【运维笔记】数据库无法启动,数据库炸后备份恢复数据
事情起因 在做docker作业的时候,把卷映射到了宿主机原来的mysql数据库目录上,宿主机原来的mysql版本为8.0,docker容器版本为5.6,导致翻车。 具体操作 备份目录 将/var/lib/mysql备份到~/mysql_backup:cp /var/lib/…...
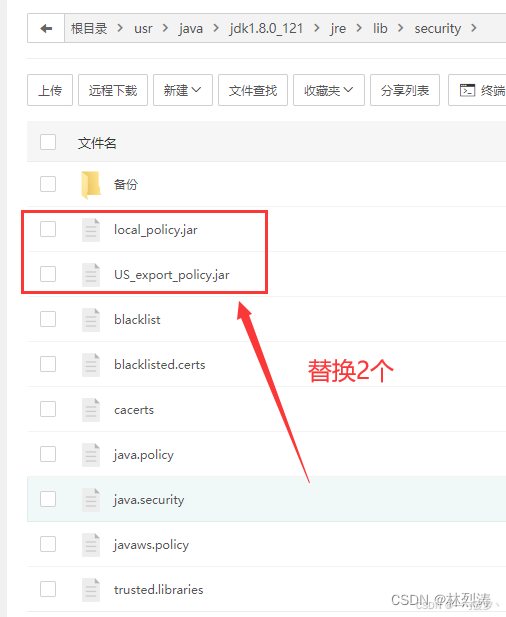
成功解决:java.security.InvalidKeyException: Illegal key size
在集成微信支付到Spring Boot项目时,可能会遇到启动报错 java.security.InvalidKeyException: Illegal key size 的问题。这是由于Java加密扩展(JCE)限制了密钥的长度。幸运的是,我们可以通过简单的替换文件来解决这个问题。 解决…...
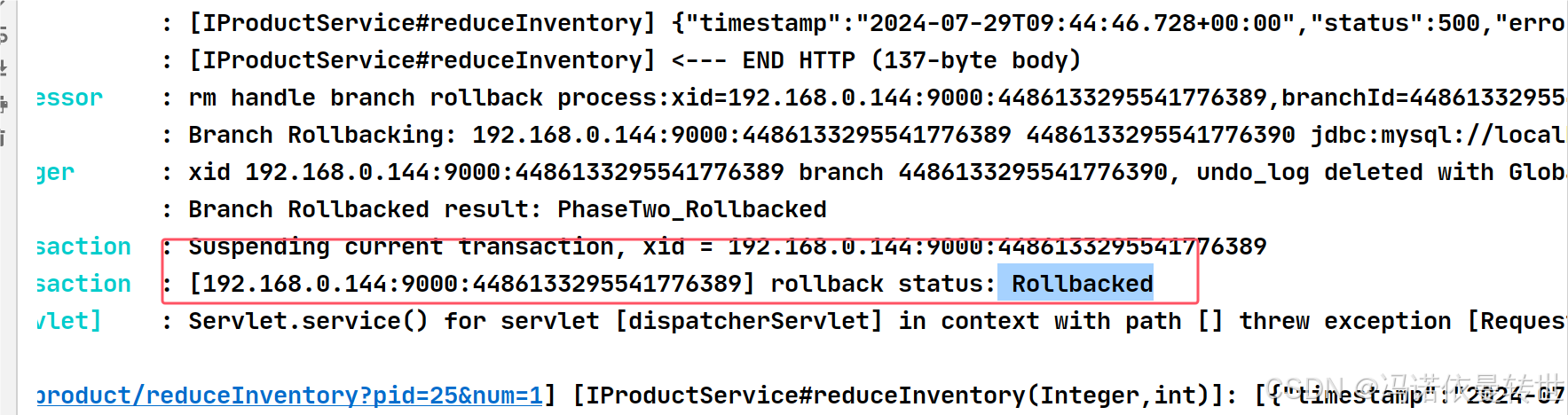
微服务事务管理(分布式事务问题 理论基础 初识Seata XA模式 AT模式 )
目录 一、分布式事务问题 1. 本地事务 2. 分布式事务 3. 演示分布式事务问题 二、理论基础 1. CAP定理 1.1 ⼀致性 1.2 可⽤性 1.3 分区容错 1.4 ⽭盾 2. BASE理论 3. 解决分布式事务的思路 三、初识Seata 1. Seata的架构 2. 部署TC服务 3. 微服务集成Se…...
—— fiddler的工作原理)
测试面试宝典(三十五)—— fiddler的工作原理
Fiddler 是一款强大的 Web 调试工具,其工作原理主要基于代理服务器的机制。 首先,当您在计算机上配置 Fiddler 为系统代理时,客户端(如浏览器)发出的所有 HTTP 和 HTTPS 请求都会被导向 Fiddler。 Fiddler 接收到这些…...

旷野之间32 - OpenAI 拉开了人工智能竞赛的序幕,而Meta 将会赢得胜利
他们通过故事做到了这一点(Snapchat 是第一个)他们用 Reels 实现了这个功能(TikTok 是第一个实现这个功能的)他们正在利用人工智能来实现这一点。 在人工智能竞赛开始时,Meta 的人工智能平台的表现并没有什么特别值得…...
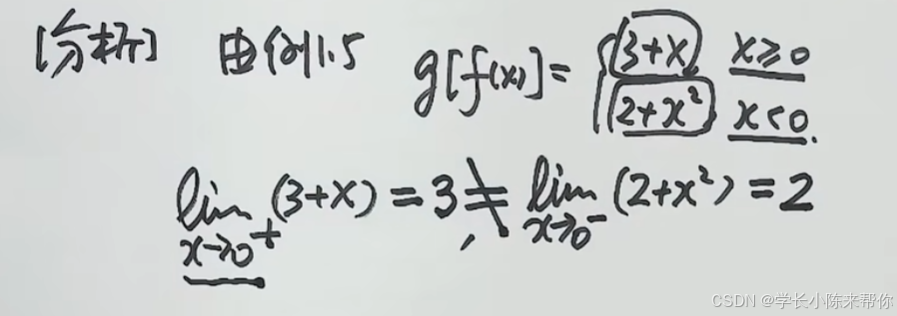
机械学习—零基础学习日志(高数15——函数极限性质)
零基础为了学人工智能,真的开始复习高数 这里我们将会学习函数极限的性质。 唯一性 来一个练习题: 再来一个练习: 这里我问了一下ChatGPT,如果一个值两侧分别趋近于正无穷,以及负无穷。理论上这个极限值应该说是不存…...

树 形 DP (dnf序)
二叉搜索子树的最大键值 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(null…...

React的生命周期?
React的生命周期分为三个主要阶段:挂载(Mounting)、更新(Updating)和卸载(Unmounting)。 1、挂载(Mounting) 当组件实例被创建并插入 DOM 时调用的生命周期方法&#x…...
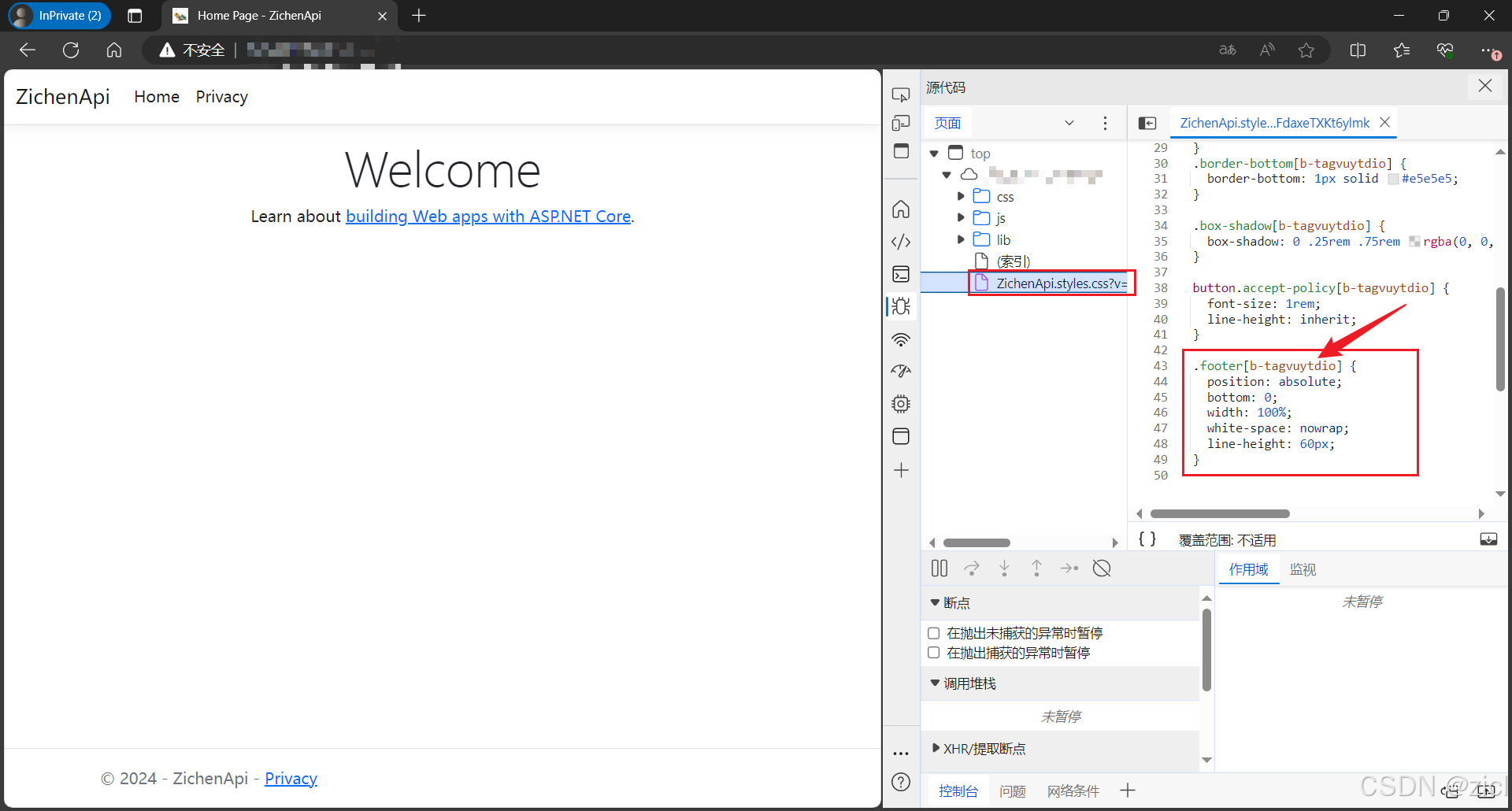
c# - - - ASP.NET Core 网页样式丢失,样式不对
c# - - - ASP.NET Core 网页样式丢失,样式不对 问题 正常样式是这样的。 修改项目名后,样式就变成这样了。底部的内容跑到中间了。 解决 重新生成解决方案,然后发布网站。 原因: 修改项目名之前的 div 上有个这个自定义属…...

Cannot find module ‘html-webpack-plugin
当你在使用Webpack构建项目时遇到Cannot find module html-webpack-plugin这样的错误,这意味着Webpack在构建过程中找不到html-webpack-plugin模块。要解决这个问题,你需要确保已经正确安装了html-webpack-plugin模块,并且在Webpack配置文件中…...

vue、react部署项目的 hashRouter 和 historyRouter模式
Vue 项目 使用 hashRouter 如果你使用的是 hashRouter,通常不需要修改 base,因为 hashRouter 使用 URL 的哈希部分来管理路由,这部分不会被服务器处理。你只需要确保 publicPath 设置正确即可。 使用 historyRouter 如果你使用的是 histo…...

Qt 实现抽屉效果
1、实现效果和UI设计界面 2、工程目录 3、mainwindow.h #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QToolButton> #include <QPushButton> #include <vector> using namespace std;QT_BEGIN_NAMESPACE namespace…...

windows上启动Kafka
官网下载 如:kafka_2.13-2.4.0.tgz 新版集成了Zookeeper ,无需另行下载 解压 至D:\Kafka\kafka_2.13-2.4.0 下 配置Kafka(可跳过) Zookeeper配置 kafka\config\zookeeper.properties下修改dataDir路径(Zookeeper数据目录)dataDirD:\\Program…...

贪心系列专题篇三
目录 单调递增的数字 坏了的计算器 合并区间 无重叠区间 用最少数量的箭 声明:接下来主要使用贪心法来解决问题!!! 单调递增的数字 题目 思路 如果我们遍历整个数组,然后对每个数k从[k,0]依次遍历寻找“单调递…...

Java中两个集合取差集
Java中两个集合取差集 说明: 集合A ListA: search archive relation test 集合B ListB: search search-gejunhao archive-gejunhao archive system 需求: 现在要取存在于A但是不存在B中的元素 test 该如何实现 思路: 在Java中,如果你想要从一个集合ÿ…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
