刷题记录:牛客NC20279[SCOI2010]序列操作
传送门:牛客
题目描述:
lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作:
0 a b 把[a, b]区间内的所有数全变成0
1 a b 把[a, b]区间内的所有数全变成1
2 a b 把[a,b]区间内的所有数全部取反,也就是说把所有的0变成1,把所有的1变成0
3 a b 询问[a, b]区间内总共有多少个1
4 a b 询问[a, b]区间内最多有多少个连续的1
对于每一种询问操作,lxhgww都需要给出回答,聪明的程序员们,你们能帮助他吗?
输入:
10 10
0 0 0 1 1 0 1 0 1 1
1 0 2
3 0 5
2 2 2
4 0 4
0 3 6
2 3 7
4 2 8
1 0 5
0 5 6
3 3 9
输出:
5
2
6
5
此题维护方式较为麻烦,需要考虑多种因素,成功写出此题之后对线段树的理解将会大大上升!!
看完题目,我们会发现显然与区间的01数量有关,并且与连续性有关
考虑用lazy=0/1lazy=0/1lazy=0/1来记录区间是否被置为0/10/10/1,用revrevrev来记录区间是否取反
用sum[0/1]sum[0/1]sum[0/1]来记录区间连续的0/10/10/1的数量,tottottot来记录区间111的数量
然后我们分析一个区间[l,r][l,r][l,r]的连续的1的数量该如何计算,我们发现可以分为3中情况,一种是该连续区间在左区间[l,mid][l,mid][l,mid],一种是该连续区间在[mid+1,r][mid+1,r][mid+1,r],还有一种是该连续区间横跨区间[l,r][l,r][l,r].对于前两种情况,我们发现sum[0/1]sum[0/1]sum[0/1]已经记录下来了.对于最后一种情况,我们发现光靠上述变量无法维护.所以此时我们使用lmax[0/1]lmax[0/1]lmax[0/1]来记录从区间的前缀0/10/10/1的最大连续数量,rmax[0/1]rmax[0/1]rmax[0/1]来记录区间的后缀0/10/10/1的最大连续数量.那么此时对于第三种情况显然就是左子树的lmax[1]lmax[1]lmax[1]+右子树的rmax[1]rmax[1]rmax[1]
现在我们来分析如何进行维护.
对于pushuppushuppushup:
tottottot可以直接维护.对于sum[]sum[]sum[],我们则需要枚举上述的三种情况来进行维护
对于lmaxlmaxlmax我们则需要判断连续区间是否能跨区间.也就是说连续的数字能否从左边界一直连续到右边界
对于rmaxrmaxrmax,与lmaxlmaxlmax同理
对于updateupdateupdate:
- 对[l,r][l,r][l,r]区间置0.此时我们的sum[],lazy,tot,lmax,rmaxsum[],lazy,tot,lmax,rmaxsum[],lazy,tot,lmax,rmax修改方式不难.需要注意的是,此时我们的修改会覆盖掉之前的revrevrev,也就是说无论之前是否进行过取反,此时我们的值都是0
- 对[l,r][l,r][l,r]区间置1.此时我们的方法和上述相同
- 对[l,r]进行取反.注意此时如果我们的区间有lazylazylazy,那就意味着我们的区间是相同的0/10/10/1,此时我们可以直接改lazylazylazy(这样做的好处是,当我们的子区间进行继承时,如果有父亲既有lazylazylazy,又有revrevrev,可以直接对lazylazylazy进行操作,忽略revrevrev).对于sum[],lazy,tot,lmax,rmaxsum[],lazy,tot,lmax,rmaxsum[],lazy,tot,lmax,rmax,我们直接调换0/10/10/1的值即可
对于pushdownpushdownpushdown:
修改的方式和updateupdateupdate相同,由父亲的lazylazylazy控制.需要注意的是如果有父亲既有lazylazylazy,又有revrevrev,可以直接对lazylazylazy进行操作,忽略revrevrev,因为在父亲的updateupdateupdate过程中,我们已经对lazylazylazy进行了相应操作
对于query1query1query1(找1的个数):
直接返回对应区间的tottottot即可
对于query2query2query2(找最长的连续1):
对于一个区间连续的1我们有三种情况(在之前分析过).对三种情况取一个maxmaxmax即可
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r;int rmax[2],lmax[2];//记录01前后缀长度int lazy,rev;//lazy记录是否被置0/1,rev记录是否被取反int sum[2];//sum1/0记录区间内最长的连续1/0的个数int tot;//记录区间内1的个数
}tree[maxn*4];
int n,m;int a[maxn];
void pushup(int rt) {int lenls=tree[ls].r-tree[ls].l+1;int lenrs=tree[rs].r-tree[rs].l+1;tree[rt].tot=tree[ls].tot+tree[rs].tot;for(int i=0;i<=1;i++) {tree[rt].sum[i]=max(tree[ls].sum[i],tree[rs].sum[i]);tree[rt].sum[i]=max(tree[rt].sum[i],tree[ls].rmax[i]+tree[rs].lmax[i]);if(tree[ls].lmax[i]==lenls) tree[rt].lmax[i]=lenls+tree[rs].lmax[i];else tree[rt].lmax[i]=tree[ls].lmax[i];if(tree[rs].rmax[i]==lenrs) tree[rt].rmax[i]=lenrs+tree[ls].rmax[i];else tree[rt].rmax[i]=tree[rs].rmax[i];}
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;tree[rt].lazy=-1;if(l==r) {if(a[l]&1) {tree[rt].rmax[1]=tree[rt].lmax[1]=1;tree[rt].sum[1]=1;tree[rt].tot=1;}else {tree[rt].rmax[0]=tree[rt].lmax[0]=1;tree[rt].sum[0]=1;}return ;}int mid=(l+r)>>1;build(lson);build(rson);pushup(rt);
}
void change(int rt,int opt) {int len=tree[rt].r-tree[rt].l+1;if(opt==0) {tree[rt].lazy=0;tree[rt].tot=0;tree[rt].sum[0]=len;tree[rt].sum[1]=0;tree[rt].rev=0;tree[rt].lmax[0]=len;tree[rt].lmax[1]=0;tree[rt].rmax[0]=len;tree[rt].rmax[1]=0;}else if(opt==1) {tree[rt].lazy=1;tree[rt].tot=len;tree[rt].sum[1]=len;tree[rt].sum[0]=0;tree[rt].rev=0;tree[rt].lmax[1]=len;tree[rt].lmax[0]=0;tree[rt].rmax[1]=len;tree[rt].rmax[0]=0;}else {if(tree[rt].lazy!=-1) {tree[rt].lazy^=1;}tree[rt].rev^=1;tree[rt].tot=len-tree[rt].tot;swap(tree[rt].lmax[0],tree[rt].lmax[1]);swap(tree[rt].rmax[0],tree[rt].rmax[1]);swap(tree[rt].sum[0],tree[rt].sum[1]);}
}
void pushdown(int rt) {if(tree[rt].lazy!=-1) {change(ls,tree[rt].lazy);change(rs,tree[rt].lazy);tree[rt].rev=0;tree[rt].lazy=-1;}else {change(ls,2);change(rs,2);tree[rt].rev=0;tree[rt].lazy=-1;}
}
void update(int l,int r,int rt,int opt) {if(tree[rt].l==l&&tree[rt].r==r) {change(rt,opt);return ;}if(tree[rt].lazy!=-1||tree[rt].rev) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) update(l,r,ls,opt);else if(l>mid) update(l,r,rs,opt);else update(l,mid,ls,opt),update(mid+1,r,rs,opt);pushup(rt);
}
int query1(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r==r) {return tree[rt].tot;}if(tree[rt].lazy!=-1||tree[rt].rev) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) return query1(l,r,ls);else if(l>mid) return query1(l,r,rs);else return query1(l,mid,ls)+query1(mid+1,r,rs);
}
int query2(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r==r) {return tree[rt].sum[1];} if(tree[rt].lazy!=-1||tree[rt].rev) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) return query2(l,r,ls);else if(l>mid) return query2(l,r,rs);else {int ans=max(query2(l,mid,ls),query2(mid+1,r,rs));int rm=min(tree[ls].rmax[1],mid-l+1);int lm=min(tree[rs].lmax[1],r-mid);ans=max(ans,lm+rm);return ans;}
}
int main() {n=read();m=read();for(int i=1;i<=n;i++) a[i]=read();build(1,n+10,1);for(int i=1;i<=m;i++) {int opt=read(),l=read(),r=read();l++;r++;if(opt==0) {update(l,r,1,0);}else if(opt==1) {update(l,r,1,1);}else if(opt==2) {update(l,r,1,2);}else if(opt==3) {printf("%d\n",query1(l,r,1));}else {printf("%d\n",query2(l,r,1));}}return 0;
}
相关文章:

刷题记录:牛客NC20279[SCOI2010]序列操作
传送门:牛客 题目描述: lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作: 0 a b 把[a, b]区间内的所有数全变成0 1 a b 把[a, b]区间内的所有数全…...

Fluent Python 笔记 第 6 章 使用一等函数实现设计模式
虽然设计模式与语言无关,但这并不意味着每一个模式都能在每一门语言中使用。1996 年,Peter Norvig 在题为“Design Patterns in Dynamic Languages”(http://norvig.com/design- patterns/)的演讲中指出,Gamma 等人合著的《设计模式:可复用面…...

windbg-应用层实时调试
调试符号windbg使用一个或多个目录来存放符号条件,并使用环境变量_NT_SYMBOL_PATH来指向这些环境变量的位置,对操作系统内部模块的符号文件,一般用http://msdl.microsoft.com/download/symbols配置如下:SRV*C:\Symbols*http://msd…...

【Python语言基础】——Python NumPy 数组索引
Python语言基础——Python NumPy 数组索引 文章目录 Python语言基础——Python NumPy 数组索引一、Python NumPy 数组索引一、Python NumPy 数组索引 访问数组元素 数组索引等同于访问数组元素。 您可以通过引用其索引号来访问数组元素。 NumPy 数组中的索引以 0 开头,这意味…...
MWORKS--MoHub介绍
MWORKS--MoHub介绍1 介绍1.1 简介1.2 功能特征2 快速上手2.1 进入工作台2.2 新建仓库并进入建模空间2.3 建模进入建模工作空间加载模型库新建模型2.4 仿真2.5 后处理曲线、动画2.6 查看模型信息3 使用手册参考1 介绍 1.1 简介 MWORKS.MoHub 支持工业知识、经验、数据的模型化…...
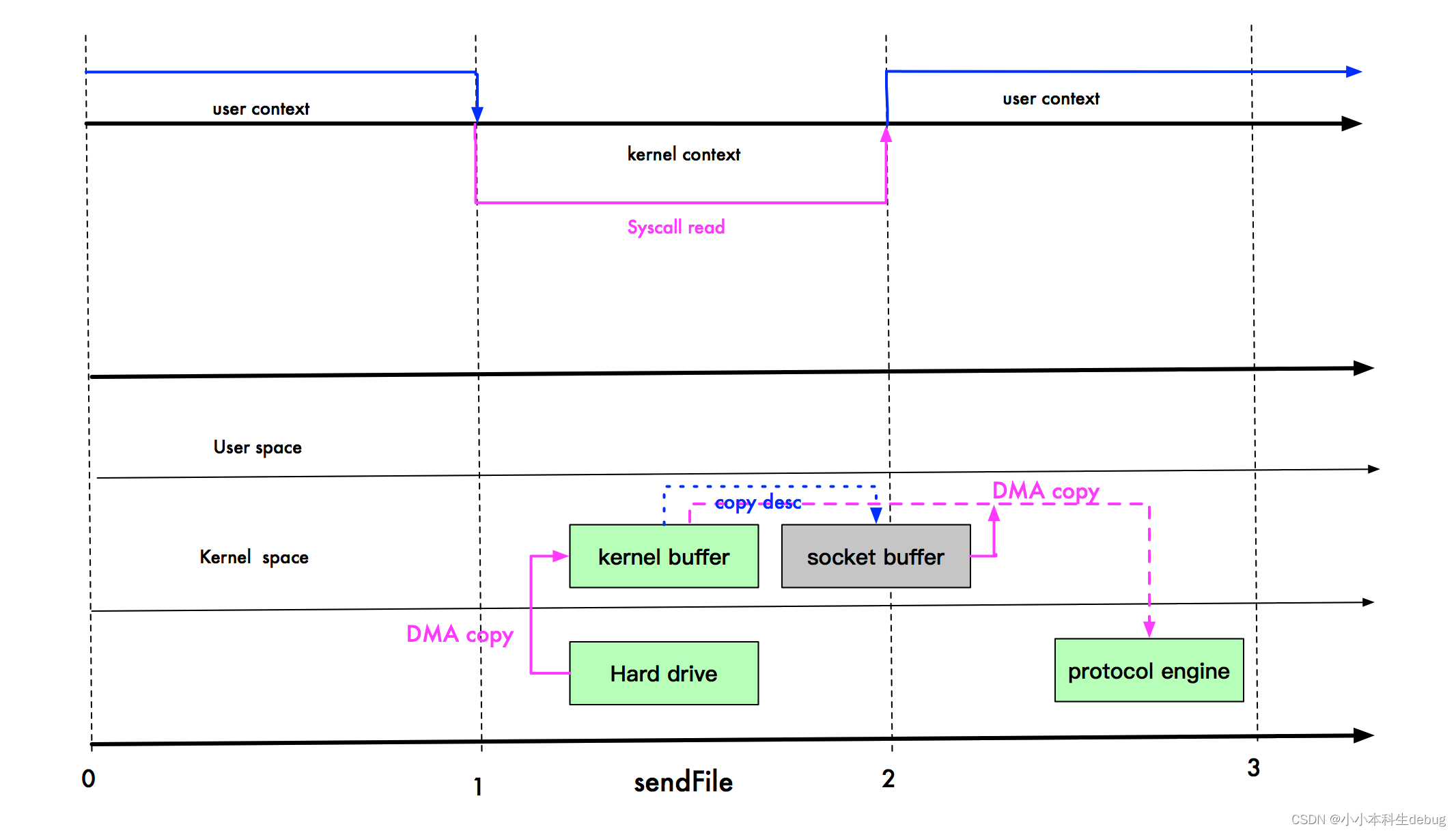
Netty零拷贝机制
Netty零拷贝机制一:用户空间与内核空间二:传统IO流程三:零拷贝常见的实现方式1. mmap write2. sendfile四:Java中零拷贝五:Netty 中如何实现零拷贝1. CompositeByteBuf 实现零拷贝2. wrap 实现零拷贝3. slice 实现零拷…...
C++:提高篇: 栈-寄存器和函数状态:windows X86-64寄存器介绍
寄存器1、什么是寄存器2、寄存器分类3、windows X86寄存器命名规则4、寄存器相关术语5、寄存器分类5.1、RAX(accumulator register)5.2、RBX(Base register)5.3、RDX(Data register)5.4、RCX(counter register)5.5、RSI(Source index)5.6、RDI(Destination index)5.7、RSP(stac…...
MyBatis-Plus入门案例
MyBatis-Plus入门案例一、MyBatis-Plus简介1、简介2、特性3、支持数据库4、框架结构5、代码及文档地址二、入门案例1、开发环境2、建库建表3、创建Spring Boot工程a>初始化工程b>引入依赖4、编写代码a>配置application.yml 或者 application.propertiesb>添加实体c…...
适用于 Windows 11/10/8/7 的 10 大数据恢复软件分享
适用于 Windows 11/10/8/7 的 最佳数据恢复软件综述。选择首选的专业数据/文件恢复软件,轻松恢复丢失的数据或删除的照片、视频等文件、SSD、外接硬盘、USB、SD卡等存储设备中的文件等。流行的sh流行的数据恢复软件也包括在内。 10 大数据恢复软件分享 为了帮助您恢…...

在线支付系列【23】支付宝支付接入指南
有道无术,术尚可求,有术无道,止于术。 文章目录前言接入指南1. 创建应用2. 绑定应用3. 配置密钥4. 上线应用5. 开通产品沙箱环境开发前准备(沙箱环境)1. 获取参数、秘钥、证书2. 下载支付宝客户端3. 案例演示前言 在之…...
linux系统常用命令
目录 一、系统介绍 二、Linux常用命令 1、Linux命令格式 2、文件目录操作命令:ls 3、文件目录操作命令:cd 4、文件目录操作命令:cat 5、文件目录操作命令:more 6、文件目录操作命令:tail 7、创建文件命令&…...
new与delete(整理) 及 内存泄露)
面试(十一)new与delete(整理) 及 内存泄露
c语言经常使用的是free与malloc,而c++又引入了new和delete它们的区别是什么呢? 内置类型 对于内置类型来说,free和delete、malloc和new几乎没什么区别,但如果是连续的空间,malloc和free只能申请和释放一块空间的内容,而new[] 和 delete[] 可以申请和释放一段连续的空间。…...

2D图像处理:2D ShapingMatching_缩放_旋转_ICP_显示ROI
文章目录 调试结果参考调试说明问题0:并行运行问题问题1:模板+Mask大小问题问题2:组合缩放和旋转问题3:可以直接将计算边缘的代码删除问题4:如何在原始图像上显示匹配到的ROI问题5:计算的原始旋转角度不需要判断,直接可以在ICP中使用问题6:绘制坐标轴问题7:绘制ROI调试…...
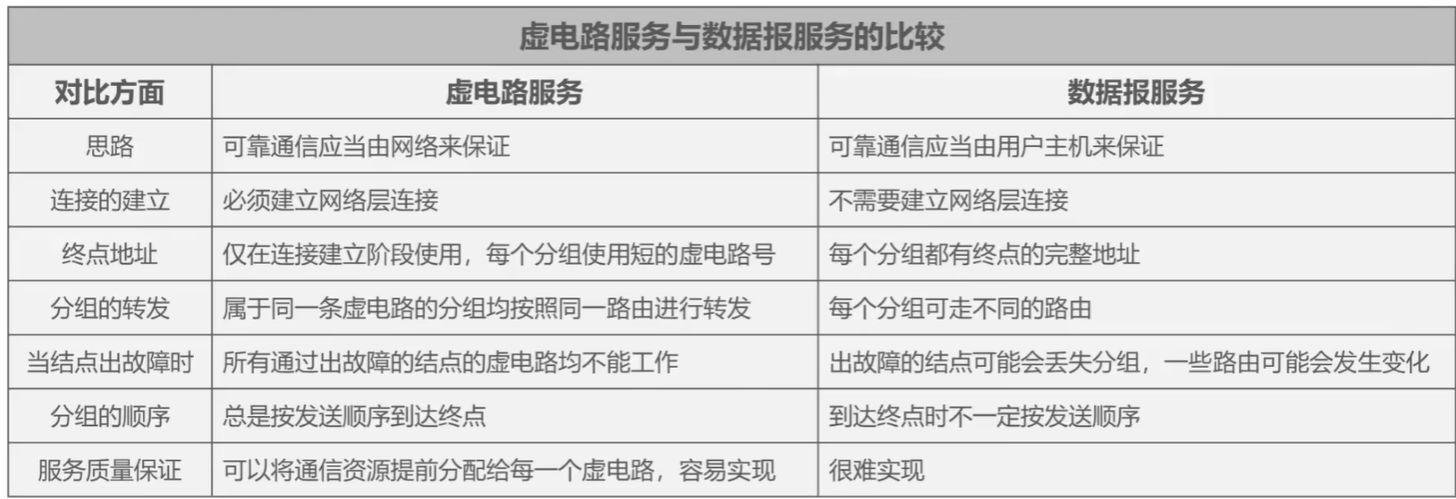
(考研湖科大教书匠计算机网络)第四章网络层-第一、二节:网络层概述及其提供的服务
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:网络层概述(1)概述(2)学习内容二:网络层提供的两种服务(1)面向连…...
概论_第8章_假设检验的基本步骤__假设检验的类型
一. 假设检验的基本步骤如下:第1步 根据实际问题提出原假设 及备择假设 , 要求 与 有且仅有一个为真;第2步 选取适当的检验统计量, 并在原假设 成立的条件下确定该检验统计量的分布;第3步 按问题的具体要求, 选取适当…...
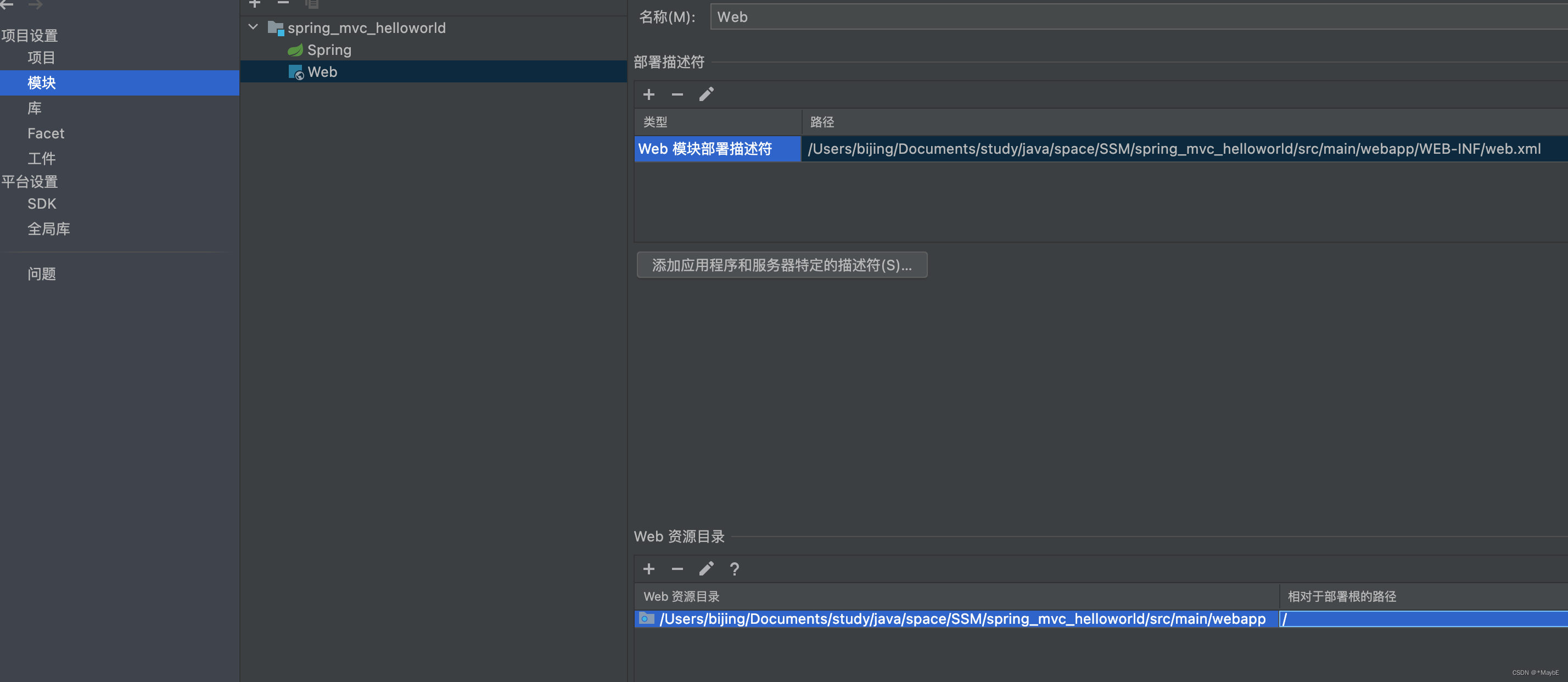
SpringMVC--简介和入门案例
SpringMVC简介 什么是MVC MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体类Bean:专门存储业务数据的,如 Studen…...
)
Cmake入门02-检测环境(笔记)
文章目录检测操作系统处理平台相关源码处理编译器相关源码编译编译处理器相关源码检查cpu是32位还是64位的检测cpu架构处理 CPU指令相关源码案例展示 Eigen3向量化加速项目设置编译器开启向量化优化《CMake cookbook》笔记检测操作系统 cmake中通过CMAKE_SYSTEM_NAME变量来识别…...

Android JNI C++读写本地文件
文章目录小结Android JNI使用CAndroid JNI读写本地文件有关权限创建文件夹访问 /storage/emulated/0/访问/data/data/example.jniwritefile/时间戳Cant determine type for tag参考小结 进行Android JNI C读写本地文件,取得了想要的效果。 Android JNI使用C 对于…...

图形化深度学习开发平台PaddleStudio(代码开源)
目录一、PaddleStudio概述二、环境准备2.1 安装PaddlePaddle2.2 安装依赖库三、基本使用介绍3.1 启动3.2 快速体验3.2.1 下载示例项目3.2.2 训练3.2.3 评估3.2.4 测试3.2.5 静态图导出四、数据集格式4.1 图像分类4.2 目标检测4.3 语义分割4.4 实例分割五、趣味项目实战…...

【力扣-LeetCode】1138. 字母板上的路径-C++题解
1138. 字母板上的路径难度中等98收藏分享切换为英文接收动态反馈我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。在本题里,字母板为board ["abcde", "fghij", "klmno", "pqrst", &quo…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
