【机器学习基础】机器学习的数学基础

【作者主页】Francek Chen
【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,依赖于强大的开源库如Scikit-learn、TensorFlow和PyTorch。本专栏介绍机器学习的相关算法以及基于Python的算法实现。
文章目录
- 一、向量
- 二、矩阵
- (一)矩阵的基本概念
- (二)矩阵运算
- (三)矩阵与线性方程组
- (四)矩阵范数
- 三、梯度
- 四、凸函数
作为一门以数据及其模型为研究对象的学科,优化模型、分析模型性能等都需要数学手段的帮助。和其他学科一样,数学可以帮我们更清晰地描述和理解机器学习算法,也可以从理论上证明算法的有效性,是机器学习中必不可少的一环。本文将会介绍机器学习中常用的数学工具,为后面的学习打下基础。
一、向量
向量(vector),在数学中指具有大小和方向的量。与向量相对,只具有大小、不具有方向的量则称为标量(scalar)。简单来说,我们可以将向量理解为由 n n n个数构成的 n n n元组,其中 n n n称为向量的维数。向量通常有两种写法,如下所示的竖排写法称为列向量:
x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} x= x1x2⋮xn 横排写法 x = ( x 1 , x 2 , … , x n ) \boldsymbol{x}=(x_1,x_2,\ldots,x_n) x=(x1,x2,…,xn) 称为行向量。一个向量如果不加说明即默认为列向量,但实际中为了节省空间,我们通常将列向量写成 x = ( x 1 , x 2 , … , x n ) T \boldsymbol{x}=(x_1, x_2, \ldots, x_n)^\mathrm{T} x=(x1,x2,…,xn)T 的形式。其中上标 T \mathrm{T} T表示转置(transpose),即将行和列翻转过来,行向量转置后就变成了列向量。例如,向量 x = ( 1 , 2 ) \boldsymbol x = (1,2) x=(1,2) 的转置为:
x T = ( 1 2 ) \boldsymbol x^\mathrm{T} = \begin{pmatrix}1 \\ 2\end{pmatrix} xT=(12)
关于向量的含义,我们既可以将其看成 n n n维空间中的一个点,其中向量每一维的值代表坐标;也可以将其看成从原点指向该坐标点的有向线段,具有长度和方向。无论哪种理解,每一个 n n n维向量都与一个 n n n维空间中的点相对应,因此,全体 n n n维向量构成的空间与 R n \mathbb{R}^n Rn是等价的。在没有额外说明的情况下,对于向量 x ∈ R n \boldsymbol{x} \in \mathbb{R}^n x∈Rn,我们用 x i ( 1 ≤ i ≤ n ) x_i (1\le i\le n) xi(1≤i≤n) 来表示其第 i i i维的分量。此外,记所有分量全部为0的向量为零向量 0 = ( 0 , 0 , … , 0 ) T \boldsymbol{0}=(0,0,\ldots,0)^\mathrm{T} 0=(0,0,…,0)T。
设向量 x , y ∈ R n \boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n x,y∈Rn,标量 a ∈ R a\in\mathbb{R} a∈R,向量的常见运算有:
- 向量相加: x + y = ( x 1 + y 1 , x 2 + y 2 , … , x n + y n ) T \boldsymbol{x} + \boldsymbol{y} =(x_1+y_1,x_2+y_2,\ldots,x_n+y_n)^\mathrm{T} x+y=(x1+y1,x2+y2,…,xn+yn)T。
- 向量与标量相乘: a x = x a = ( a x 1 , a x 2 , … , a x n ) T a\boldsymbol{x} = \boldsymbol{x}a = (ax_1,ax_2,\ldots,ax_n)^\mathrm{T} ax=xa=(ax1,ax2,…,axn)T。当 a = 0 a=0 a=0 或 x = 0 \boldsymbol x = \boldsymbol 0 x=0 时,结果即为 0 \boldsymbol 0 0。
- 向量内积(inner product),也称向量点积(dot product): x ⋅ y = ∑ i = 1 n x i y i \boldsymbol{x}\cdot\boldsymbol{y} = \sum_{i=1}^n x_iy_i x⋅y=∑i=1nxiyi,注意两个向量的内积结果是标量。从式中可以看出,向量内积满足交换律,即 x ⋅ y = y ⋅ x \boldsymbol{x}\cdot\boldsymbol{y} = \boldsymbol{y}\cdot\boldsymbol{x} x⋅y=y⋅x。
为了衡量向量的“长度”,我们定义范数(norm)函数 ∥ ⋅ ∥ : R n → R \| \cdot \| \colon \mathbb{R}^n \to \mathbb{R} ∥⋅∥:Rn→R。一个函数是范数,当且仅当其满足下面3个条件:
(1)正定性: ∥ x ∥ ≥ 0 \|\boldsymbol{x}\| \ge 0 ∥x∥≥0,当且仅当 x = 0 \boldsymbol{x}=\boldsymbol{0} x=0 时, ∥ x ∥ = 0 \|\boldsymbol{x}\|=0 ∥x∥=0;
(2)绝对齐次性: ∥ a x ∥ = ∣ a ∣ ∥ x ∥ \| a\boldsymbol{x} \| = |a|\|\boldsymbol{x}\| ∥ax∥=∣a∣∥x∥;
(3)三角不等式: ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ \| \boldsymbol{x} + \boldsymbol{y} \| \le \|\boldsymbol{x}\| + \|\boldsymbol{y}\| ∥x+y∥≤∥x∥+∥y∥。
在各种各样的向量范数中, L p L_p Lp范数(又称 p p p范数)是一类相对常用的范数,其定义为
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 / p , p ≥ 1 \|\boldsymbol{x}\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{1/p},\quad p \ge 1 ∥x∥p=(i=1∑n∣xi∣p)1/p,p≥1 其中,又以下面几种 L p L_p Lp范数最为常见:
- L 2 L_2 L2范数,又称欧几里得范数,其结果是向量对应的点到原点的欧氏距离,也称为向量的模长: ∥ x ∥ 2 = ∑ i = 1 n x i 2 \|\boldsymbol{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2} ∥x∥2=i=1∑nxi2 由于其应用最广,我们有时会省略 L 2 L_2 L2范数的下标,直接写为 ∥ x ∥ \|\boldsymbol{x}\| ∥x∥。
- L 1 L_1 L1范数,又称绝对值范数,为向量各个分量的绝对值之和,其结果是向量所表示的点到原点的曼哈顿距离: ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|\boldsymbol{x}\|_1 = \sum_{i=1}^n |x_i| ∥x∥1=i=1∑n∣xi∣
- L ∞ L_\infty L∞范数,又称无穷范数,由对 L p L_p Lp范数的定义取极限 p → + ∞ p\to+\infty p→+∞ 得到,其结果是向量中绝对值最大的分量: ∥ x ∥ ∞ = max i = 1 , … , n ∣ x i ∣ \|\boldsymbol{x}\|_\infty = \max_{i=1,\ldots,n} |x_i| ∥x∥∞=i=1,…,nmax∣xi∣
当 0 < p < 1 0 < p < 1 0<p<1 时,按与上面相同的方式定义的函数并不满足范数的条件。但是为了方便,我们常将下面的函数也称为“范数”:
- L 0 L_0 L0范数,由对 L p L_p Lp范数的定义取极限 p → 0 + p \to 0^+ p→0+ 得到,其结果是向量中不为 0 0 0的元素的个数: ∥ x ∥ 0 = ∑ i = 1 n I ( x i ≠ 0 ) \|\boldsymbol{x}\|_0 = \sum_{i=1}^n \mathbb{I}(x_i \neq 0) ∥x∥0=i=1∑nI(xi=0)
二、矩阵
向量是一些数在一维上构成的元组,如果把它朝二维扩展,我们就得到了矩阵(matrix)。与向量相比,矩阵由于有了更多的维数,具有更大的灵活性,还可以定义新的运算。下面,我们就来介绍矩阵的基本概念和本书中可能会用到的简单性质。
(一)矩阵的基本概念
矩阵是由一些数构成的矩形元组。一个 m m m行 n n n列的矩阵通常称为 m × n m \times n m×n 的矩阵,记为
A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) \boldsymbol{A} = \begin{pmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots\ & &\vdots \\ a_{m1} &a_{m2} &\cdots &a_{mn} \end{pmatrix} A= a11a21⋮am1a12a22⋮ am2⋯⋯⋯a1na2n⋮amn
对具体的元素不关心时,我们也将其记为 A m × n \boldsymbol{A}_{m\times n} Am×n或 A \boldsymbol A A。默认情况下,我们用 a i j a_{ij} aij或者 A i j \boldsymbol{A}_{ij} Aij来表示矩阵 A \boldsymbol{A} A中位于第 i i i行第 j j j列的元素,有时也反过来用 ( a i j ) m × n (a_{ij})_{m\times n} (aij)m×n 表示元素为 a i j a_{ij} aij的 m m m行 n n n列矩阵。与向量相似, m × n m\times n m×n 的实数矩阵构成的空间即与 m × n m\times n m×n 维的实数空间等价,一般记为 R m × n \mathbb{R}^{m\times n} Rm×n。向量实际上是一种特殊的矩阵,列向量的列数为1,行向量的行数为1。同时,矩阵也可以看作由一组向量构成。设 a i = ( a 1 i , a 2 i , … , a m i ) T \boldsymbol{a}_i=(a_{1i}, a_{2i},\ldots, a_{mi})^\mathrm{T} ai=(a1i,a2i,…,ami)T,那么 A = ( a 1 , a 2 , … , a n ) \boldsymbol{A}=(\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots, \boldsymbol{a}_n) A=(a1,a2,…,an)。与向量相似,矩阵同样存在转置操作,表示将矩阵的行和列交换。一个 m × n m\times n m×n 矩阵 ( a i j ) m × n (a_{ij})_{m\times n} (aij)m×n 转置后会得到 n × m n \times m n×m 矩阵 ( a j i ) n × m (a_{ji})_{n\times m} (aji)n×m。例如,矩阵
A = ( 1 2 3 4 5 6 ) \boldsymbol A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} A= 135246 的转置为
A T = ( 1 3 5 2 4 6 ) \boldsymbol A^\mathrm{T} = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} AT=(123456)
特别地,行数和列数均为 n n n的矩阵称为 n n n阶方阵。如果 n n n阶方阵 D \boldsymbol D D只有左上到右下的对角线上的元素不为0,则称该方阵为对角矩阵(diagonal matrix),记为 d i a g ( a 1 , a 2 , … , a n ) \mathrm{diag}(a_1,a_2,\ldots,a_n) diag(a1,a2,…,an)。例如 d i a g ( 1 , 2 , 3 ) \mathrm{diag}(1, 2, 3) diag(1,2,3) 代表的矩阵为
d i a g ( 1 , 2 , 3 ) = ( 1 0 0 0 2 0 0 0 3 ) \mathrm{diag}(1,2,3) = \begin{pmatrix} 1 & 0 & 0\\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix} diag(1,2,3)= 100020003
进一步,如果对角矩阵对角线上的元素全部为1,则称该方阵为 n n n阶单位矩阵(identity matrix)或单位阵,用 I n \boldsymbol{I}_n In表示。阶数明确时,也可以省略下标的阶数,记为 I \boldsymbol{I} I。例如,三阶单位阵为
I 3 = ( 1 0 0 0 1 0 0 0 1 ) \boldsymbol I_3 = \begin{pmatrix} 1 &0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} I3= 100010001 所有元素为零的矩阵称为单位零矩阵,记为 0 \boldsymbol 0 0。
(二)矩阵运算
设矩阵 A , B ∈ R m × n \boldsymbol{A},\boldsymbol{B} \in \mathbb{R}^{m\times n} A,B∈Rm×n, C ∈ R n × l \boldsymbol{C} \in \mathbb{R}^{n\times l} C∈Rn×l, D ∈ R l × k \boldsymbol{D} \in \mathbb{R}^{l\times k} D∈Rl×k, P ∈ R m × l \boldsymbol{P} \in \mathbb{R}^{m\times l} P∈Rm×l。向量 x ∈ R n \boldsymbol{x} \in \mathbb{R}^n x∈Rn,标量 λ ∈ R \lambda \in \mathbb{R} λ∈R。矩阵的常用运算有:
- 矩阵相加: A + B = B + A = ( a i j + b i j ) m × n \boldsymbol{A} + \boldsymbol{B} = \boldsymbol{B} + \boldsymbol{A} = (a_{ij} + b_{ij})_{m\times n} A+B=B+A=(aij+bij)m×n 要求两个矩阵行列数目都相同。
- 矩阵与标量相乘: λ A = A λ = ( λ ⋅ a i j ) m × n \lambda\boldsymbol{A}=\boldsymbol{A}\lambda=(\lambda \cdot a_{ij})_{m\times n} λA=Aλ=(λ⋅aij)m×n。
- 矩阵与矩阵相乘,要求第一个矩阵的列数与第二个矩阵的行数相同。设 P = A C \boldsymbol{P}=\boldsymbol{A}\boldsymbol{C} P=AC,则有 p i j = ∑ t = 1 n a i t c t j p_{ij} = \sum_{t=1}^n a_{it}c_{tj} pij=t=1∑naitctj
最终得到的 P \boldsymbol{P} P是 m × l m\times l m×l 维的矩阵。这一运算方式可以理解为, P \boldsymbol P P的第 i i i行 j j j列的元素 p i j p_{ij} pij是由 A \boldsymbol A A的第 i i i行和 B \boldsymbol B B的第 j j j列做向量内积得到的。这也说明了为什么矩阵乘法要求第一个矩阵的列数(即行向量的维数)与第二个矩阵的行数(即列向量的维数)相同,因为只有维数相等的向量才能进行内积。例如:
( 1 0 2 0 2 1 ) × ( 2 0 1 3 3 2 ) = ( 8 4 5 8 ) \begin{pmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \end{pmatrix} \times \begin{pmatrix} 2 & 0 \\ 1 & 3 \\ 3 & 2 \end{pmatrix} = \begin{pmatrix} 8 & 4 \\ 5 & 8 \end{pmatrix} (100221)× 213032 =(8548) 其中, P \boldsymbol P P第1行第1列的8的计算过程为
( 1 , 0 , 2 ) ( 2 1 3 ) = 1 × 2 + 0 × 1 + 2 × 3 = 8 (1,0,2) \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} = 1\times 2 + 0 \times 1 + 2 \times 3 = 8 (1,0,2) 213 =1×2+0×1+2×3=8 其余元素以此类推。
应当注意,由于矩阵乘法对行数和列数的要求,将 A C \boldsymbol{A}\boldsymbol{C} AC交换成 C A \boldsymbol{C}\boldsymbol{A} CA并不一定还符合乘法的定义。即使 A \boldsymbol{A} A与 C \boldsymbol{C} C的维数形如 m × n m \times n m×n 和 n × m n \times m n×m,交换后仍然满足乘法定义,其交换前后相乘的结果也不一定相等,即 A C ≠ C A \boldsymbol{A}\boldsymbol{C} \neq \boldsymbol{C}\boldsymbol{A} AC=CA。例如:
( 1 1 0 1 ) × ( 0 1 1 1 ) = ( 1 2 1 1 ) , ( 0 1 1 1 ) × ( 1 1 0 1 ) = ( 0 1 1 2 ) \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \times \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix},\quad \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 2 \end{pmatrix} (1011)×(0111)=(1121),(0111)×(1011)=(0112)
不过,虽然矩阵的乘法不满足交换律,但依然满足结合律,即 ( A C ) D = A ( C D ) (\boldsymbol{A}\boldsymbol{C})\boldsymbol{D} = \boldsymbol{A} (\boldsymbol{C}\boldsymbol{D}) (AC)D=A(CD)。另外,对于转置操作,有 ( A C ) T = C T A T (\boldsymbol{A}\boldsymbol{C})^\mathrm{T} = \boldsymbol{C}^\mathrm{T} \boldsymbol{A}^\mathrm{T} (AC)T=CTAT。
由于向量也是一种特殊的矩阵,向量内积其实是矩阵乘法的一种特殊形式。但是,两个 n × 1 n \times 1 n×1 维的列向量并不满足矩阵乘法对维数的要求。为了将向量的内积与矩阵乘法统一,我们通常将其中一个向量转置成 1 × n 1 \times n 1×n 维的行向量,再按矩阵乘法的规则进行计算,即:
x ⋅ y = y T x \boldsymbol x \cdot \boldsymbol y = \boldsymbol y^\mathrm{T} \boldsymbol x x⋅y=yTx 此外,内积也常用尖括号写为 ⟨ x , y ⟩ \langle \boldsymbol x, \boldsymbol y \rangle ⟨x,y⟩。该写法只是一种形式,其计算规则和上面是相同的。
矩阵可以与向量相乘,其计算方式与矩阵乘法相同。设 z = A x \boldsymbol{z} = \boldsymbol{A}\boldsymbol{x} z=Ax,那么
z i = ∑ t = 1 n a i t x t z_i = \sum_{t=1}^n a_{it}x_t zi=t=1∑naitxt 得到的 z \boldsymbol{z} z是 m m m维向量。例如:
( 1 0 2 2 1 1 ) × ( 0 3 1 ) = ( 2 4 ) \begin{pmatrix} 1 & 0 & 2 \\ 2 & 1 & 1 \end{pmatrix} \times \begin{pmatrix} 0 \\ 3 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} (120121)× 031 =(24)
类似于实数中的 1 1 1,任何矩阵与维度相符的单位阵相乘都等于自身,即 A m × n I n = I m A m × n = A m × n \boldsymbol{A}_{m\times n} \boldsymbol{I}_n = \boldsymbol{I}_m \boldsymbol{A}_{m\times n} = \boldsymbol{A}_{m\times n} Am×nIn=ImAm×n=Am×n。进一步,在实数中,相乘等于 1 1 1的两个数互为倒数。利用单位矩阵,我们也可以定义矩阵的“倒数”——逆矩阵(inverse)。对于 n n n阶方阵 A \boldsymbol{A} A,如果存在 n n n阶方阵 B \boldsymbol{B} B满足 A B = I \boldsymbol{A}\boldsymbol{B}=\boldsymbol{I} AB=I,则称 B \boldsymbol{B} B是 A \boldsymbol{A} A的逆矩阵,记为 B = A − 1 \boldsymbol{B} = \boldsymbol{A}^{-1} B=A−1。逆矩阵之间的乘法是可交换的,即 A A − 1 = A − 1 A = I \boldsymbol{A}\boldsymbol{A}^{-1} = \boldsymbol{A}^{-1}\boldsymbol{A} = \boldsymbol{I} AA−1=A−1A=I。例如:
( 1 1 0 1 ) × ( 1 − 1 0 1 ) = ( 1 0 0 1 ) , ( 1 − 1 0 1 ) × ( 1 1 0 1 ) = ( 1 0 0 1 ) \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix},\quad \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} (1011)×(10−11)=(1001),(10−11)×(1011)=(1001)
转置操作与求逆操作之间的顺序可以交换,即 ( A T ) − 1 = ( A − 1 ) T (\boldsymbol{A}^\mathrm{T})^{-1} = (\boldsymbol{A}^{-1})^\mathrm{T} (AT)−1=(A−1)T。
(三)矩阵与线性方程组
矩阵的逆并不是一定存在的。例如,二阶矩阵
A = ( 1 − 1 − 1 1 ) \boldsymbol A = \left(\begin{matrix} 1 & -1 \\ -1 & 1 \end{matrix}\right) A=(1−1−11) 就不存在逆矩阵。显然,零矩阵也不存在逆矩阵。那么,什么情况下矩阵的逆存在呢?我们可以从多元一次方程组的角度来理解。设矩阵 A n × n ∈ R n × n \boldsymbol A_{n\times n}\in \mathbb{R}^{n\times n} An×n∈Rn×n,向量 x ∈ R n \boldsymbol x \in \mathbb{R}^n x∈Rn。将方程 A x = 0 \boldsymbol A\boldsymbol x = \boldsymbol 0 Ax=0 按矩阵与向量的乘法展开,得到
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = 0 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = 0 ⋮ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = 0 \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = 0 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = 0 \\ \quad\quad\vdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = 0 \\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=0a21x1+a22x2+⋯+a2nxn=0⋮an1x1+an2x2+⋯+annxn=0 这是一个 n n n元一次方程组,且显然有解 x = 0 \boldsymbol x= \boldsymbol 0 x=0。如果该方程组只有这一个解,那么矩阵 A \boldsymbol A A的逆存在;反之,如果方程组存在非零解,则矩阵的逆不存在。设 x 1 \boldsymbol x_1 x1是方程的一个非零解,满足 A x 1 = 0 \boldsymbol A \boldsymbol x_1 = \boldsymbol 0 Ax1=0,假设矩阵的逆存在,那么:
0 = A − 1 0 = A − 1 A x 1 = I x 1 = x 1 \boldsymbol 0 = \boldsymbol A^{-1}\boldsymbol 0 = \boldsymbol A^{-1}\boldsymbol A \boldsymbol x_1 = \boldsymbol I \boldsymbol x_1 = \boldsymbol x_1 0=A−10=A−1Ax1=Ix1=x1 由此得到 x 1 = 0 \boldsymbol x_1=\boldsymbol 0 x1=0,与 x 1 \boldsymbol x_1 x1是非零解矛盾,故矩阵的逆不存在。
我们用上面举的二阶矩阵的例子来进一步说明这一现象,该矩阵对应的方程组为
{ + x 1 − x 2 = 0 − x 1 + x 2 = 0 \begin{cases} +x_1 &- x_2 &= 0 \\ -x_1 &+ x_2 &= 0 \end{cases} {+x1−x1−x2+x2=0=0 可以发现,如果将第一个方程乘上-1,就得到了第二个方程。因此,这两个方程事实上是一样的,方程组其实只包含一个方程 x 1 − x 2 = 0 x_1-x_2=0 x1−x2=0。最终,方程组有两个未知数,但只有一个方程,就存在无穷多组解,从而矩阵的逆不存在。
如果方程组 A x = 0 \boldsymbol {Ax} = \boldsymbol0 Ax=0 存在非零解,不妨设解向量中的前 m m m维 x 1 , x 2 , … , x m x_1,x_2,\ldots, x_m x1,x2,…,xm 不为零。否则,我们总可以重排矩阵和向量行的顺序来使不为零的维度变成前 m m m维。设矩阵 A \boldsymbol A A的列向量为 a 1 , a 2 , … , a n \boldsymbol a_1, \boldsymbol a_2, \ldots, \boldsymbol a_n a1,a2,…,an,那么非零解就对应着下面的关系:
x 1 a 1 + x 2 a 2 + ⋯ + x m a m = 0 x_1 \boldsymbol a_1 + x_2 \boldsymbol a_2 + \cdots + x_m \boldsymbol a_m = \boldsymbol 0 x1a1+x2a2+⋯+xmam=0 也就是说,原方程组中至少有一个方程可以由其他方程线性组合得到。像这样,对于向量 u 1 , … , u n \boldsymbol u_1, \ldots, \boldsymbol u_n u1,…,un,如果以 t i t_i ti为未知数的方程 ∑ i = 1 n t i u i = 0 \sum_{i=1}^n t_i \boldsymbol u_i = \boldsymbol 0 i=1∑ntiui=0 有非零解,就称向量组 u 1 , … , u n \boldsymbol u_1, \ldots, \boldsymbol u_n u1,…,un 是线性相关的;反之,如果该方程只有零解,就称向量组是线性无关的。而对于线性相关的向量组,设其中存在 m m m个向量线性无关,而任取 m + 1 m+1 m+1个向量都线性相关,则称该向量组的秩(rank)为 m m m,记为 R a n k ( u 1 , … , u n ) = m \mathrm{Rank}(\boldsymbol u_1, \ldots, \boldsymbol u_n) = m Rank(u1,…,un)=m。线性无关的向量组的秩就等于其包含向量的个数。将这一概念应用到矩阵上,可以定义矩阵 A \boldsymbol A A的秩 R a n k ( A ) \mathrm{Rank}(\boldsymbol A) Rank(A)为其列向量组成的向量组的秩。于是,我们可以用矩阵的秩来判断其是否可逆:方阵 A n × n \boldsymbol A_{n\times n} An×n可逆的充分必要条件是 R a n k ( A ) = n \mathrm{Rank}(\boldsymbol A)=n Rank(A)=n。
直观上来说,矩阵的秩可以衡量矩阵包含的信息,也就是矩阵的复杂程度。例如在上面的线性方程组中,虽然它包含两个方程,但由其中一个方程可以推出另一个,说明它包含的信息与仅有一个方程没有什么区别。对于矩阵来说,矩阵的秩越低,其列向量之间的相关性就越强,说明其实际上包含的信息就越少。
(四)矩阵范数
与向量类似,在矩阵上同样可以定义范数函数 ∥ ⋅ ∥ : R m × n → R \| \cdot \| \colon \mathbb{R}^{m\times n} \to \mathbb{R} ∥⋅∥:Rm×n→R,其需要满足的条件也与向量范数相同。
(1)正定性: ∥ A ∥ ≥ 0 \|\boldsymbol{A}\| \ge 0 ∥A∥≥0,且 ∥ A ∥ = 0 \|\boldsymbol{A}\| = 0 ∥A∥=0 当且仅当 A \boldsymbol{A} A的所有元素都为 0 0 0。
(2)绝对齐次性: ∥ a A ∥ = ∣ a ∣ ∥ A ∥ \| a\boldsymbol{A} \| = |a|\| \boldsymbol{A} \| ∥aA∥=∣a∣∥A∥。
(3)三角不等式: ∥ A + B ∥ ≤ ∥ A ∥ + ∥ B ∥ \| \boldsymbol{A} + \boldsymbol{B} \| \le \| \boldsymbol{A} \| + \| \boldsymbol{B} \| ∥A+B∥≤∥A∥+∥B∥。
在机器学习中,较为常用的矩阵范数是弗罗贝尼乌斯范数(Frobenius norm),简称 F \mathrm{F} F范数,定义为矩阵每个元素的平方之和的平方根: ∥ A ∥ F = ( ∑ i = 1 m ∑ j = 1 n a i j 2 ) 1 2 \| \boldsymbol{A} \|_\mathrm{F} = \left( \sum_{i=1}^m \sum_{j=1}^n a_{ij}^2 \right)^{\frac{1}{2}} ∥A∥F=(i=1∑mj=1∑naij2)21 F \mathrm{F} F范数与向量的 L 2 L_2 L2范数的定义较为类似,直观来说,可以用来衡量矩阵整体的“大小”,或者可以理解为将矩阵拉成向量后,向量对应的模长。
三、梯度
在机器学习中,我们经常会将问题抽象成数学模型,经过一系列推导后,将其转化为在一定约束条件下,求某个函数在空间上的最小值的问题,这样的问题就叫做优化问题。给定函数 f : R n → R f\colon \mathbb{R}^n \to \mathbb{R} f:Rn→R,最简单也是最自然的优化问题是寻找函数的最小值: min x f ( x ) \min_{\boldsymbol{x}} f(\boldsymbol{x}) xminf(x)
要求解这一优化问题,就必须分析该函数的性质,尤其是函数的变化趋势。试想,如果知道了函数在空间的每一个地方沿着任一方向是上升还是下降,就可以不断沿着函数值下降的方向走,直到向周围的所有方向函数值都上升为止。这时,我们就找到了函数的一个局部极小值。当然,这里描述的只是某种直观的感受,并不完全严谨,但也提示了函数的变化趋势在优化问题中的重要性。而梯度,就是描述函数变化速率和方向的工具。
假设有一定微积分的基础,下面给出梯度(gradient)的定义。对于向量的标量值函数 f : R n → R f \colon \mathbb{R}^n \to \mathbb{R} f:Rn→R,其在 x \boldsymbol{x} x处的梯度为 ∇ x f ( x ) = ( ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ) T \nabla_{\boldsymbol{x}} f(\boldsymbol{x}) = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right)^\mathrm{T} ∇xf(x)=(∂x1∂f,∂x2∂f,⋯,∂xn∂f)T 其中, ∇ x \nabla_{\boldsymbol{x}} ∇x表示对变量 x \boldsymbol{x} x求梯度。在不引起混淆的情况下,下标 x \boldsymbol{x} x可以省略。可以看出, ∇ f \nabla f ∇f也是一个 n n n维向量,与 x \boldsymbol{x} x形状相同,其每一维均由 f f f对 x \boldsymbol{x} x的对应维度求偏导数得到。我们知道,多元函数对其中一个变量的偏导数代表了函数在该变量方向上的变化速率和方向。如果将向量函数的变量 x \boldsymbol{x} x看作是 n n n个独立的标量变量,那么 f f f也可以认为是有 n n n个变量的多元函数 f ( x 1 , … , x n ) f(x_1, \ldots, x_n) f(x1,…,xn)。并且在直角坐标系中,由于向量的每一维都对应一个坐标轴, f f f对每个维度的偏导数,就指示了函数在这一坐标轴方向上的变化情况。最终由各个偏导数组合而成的向量,则代表函数在空间中完整的变化速率与方向。
值得注意的是,梯度向量所指的方向有非常特殊的性质。如图1所示,图中是函数 f ( x , y ) = − x − 2 y f(x,y) = -x - 2y f(x,y)=−x−2y 在 x y xy xy平面上的等值线图,在每条直线上函数的值都相等,且颜色越偏红的地方函数值越大,越偏蓝的地方函数值越小。按照上面的运算规则,可以算出函数在点 ( 1 , 1 ) (1,1) (1,1) 处的梯度是 ( − 1 , − 2 ) (-1,-2) (−1,−2)。图中画出了以 ( 1 , 1 ) (1,1) (1,1) 为起点的一些箭头,图例中标明了箭头的方向,其中蓝色实线箭头是梯度方向。这些箭头的长度都相等。可以看出,虽然沿所有箭头的方向函数值都在增大,但是蓝色的箭头跨过了最多的等值线,说明沿该方向函数值增大最快。

或许有人对图1有疑问,认为函数非线性的情况与图中展示的线性情况不同,函数值增大最快的方向应当是从起点指向最大值点的方向。然而,仿照一元函数的泰勒展开 f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) \approx f(x_0) + f'(x_0)(x-x_0) f(x)≈f(x0)+f′(x0)(x−x0),我们也可以利用梯度对标量值函数在局部进行线性近似,即 f ( x ) ≈ f ( x 0 ) + ∇ f ( x 0 ) T ( x − x 0 ) f(\boldsymbol x) \approx f(\boldsymbol x_0) + \nabla f(\boldsymbol x_0)^\mathrm{T} (\boldsymbol x - \boldsymbol x_0) f(x)≈f(x0)+∇f(x0)T(x−x0) 在遇到的情境中,函数 f f f的性质通常都足够好,可以进行上面的线性近似。因此,当我们讨论函数在一个很小局部内的变化时,总是可以认为函数是线性的。这样,参照上面线性函数的例子,就可以从直观上推出:在某一点函数值上升最快的方向就是函数在该点梯度的方向。更严格的数学证明应当考虑函数在起点 x 0 \boldsymbol x_0 x0沿不同方向的方向导数 ∂ f ( x 0 ) ∂ s \begin{aligned}\frac{\partial f(\boldsymbol x_0)}{\partial \boldsymbol s}\end{aligned} ∂s∂f(x0),其中 s \boldsymbol s s表示空间中的某个方向。该导数的含义是,自变量从 x 0 \boldsymbol x_0 x0沿方向 s \boldsymbol s s变为 x 0 + d s \boldsymbol x_0 + \mathrm{d}\boldsymbol s x0+ds时,函数值的变化为 ∥ ∂ f ( x 0 ) ∂ s ∥ \begin{aligned}\left\lVert \frac{\partial f(\boldsymbol x_0)}{\partial \boldsymbol s} \right\rVert\end{aligned} ∂s∂f(x0) 。利用方向导数可以证明,当函数值变化最大时, s \boldsymbol s s就是梯度方向。
图2展示了几个有代表性的二元函数在空间中部分点的梯度,分别是抛物面 f ( x , y ) = x 2 + y 2 f(x,y)=x^2+y^2 f(x,y)=x2+y2,马鞍面 f ( x , y ) = x 2 − y 2 f(x,y)=x^2-y^2 f(x,y)=x2−y2,以及 f ( x , y ) = sin ( x ) sin ( y ) f(x,y)=\sin(x)\sin(y) f(x,y)=sin(x)sin(y)。



上文介绍的函数以向量为自变量,函数值是标量。除此之外,在机器学习中我们还会经常遇到自变量和函数值都是向量的函数,称为向量值函数。设 f : R n → R m \boldsymbol{f} \colon \mathbb{R}^n \to \mathbb{R}^m f:Rn→Rm 是向量值函数,那么函数值的每一维都是一个 n n n元标量函数: f ( x ) = ( f 1 ( x 1 , … , x n ) , f 2 ( x 1 , … , x n ) , ⋯ , f m ( x 1 , … , x n ) ) T \boldsymbol f(\boldsymbol x) = \left(f_1(x_1,\ldots,x_n), f_2(x_1,\ldots,x_n), \cdots, f_m(x_1,\ldots,x_n)\right)^\mathrm{T} f(x)=(f1(x1,…,xn),f2(x1,…,xn),⋯,fm(x1,…,xn))T
向量值函数其实并不少见,半径为 r r r的圆的参数方程 x = r cos θ , y = r sin θ x=r\cos\theta, y=r\sin\theta x=rcosθ,y=rsinθ 就可以看成自变量为 θ \theta θ、函数值为向量 ( x , y ) (x,y) (x,y)的函数。假如我们要描述空间中的风速,那么也需要一个从空间坐标 ( x , y , z ) (x,y,z) (x,y,z)到风速 ( v x , v y , v z ) (v_x,v_y,v_z) (vx,vy,vz)的向量值函数。而在机器学习中,我们最常见的是向量之间的线性变换 f ( x ) = A x \boldsymbol f(\boldsymbol x) = \boldsymbol A\boldsymbol x f(x)=Ax,其中 A \boldsymbol A A是矩阵。
向量值函数同样也可以对自变量求导数,但这时导数的结果就变成矩阵,称为雅可比矩阵(Jacobian matrix),通常用 ∇ f \nabla \boldsymbol f ∇f或者 J f \boldsymbol J_{\boldsymbol f} Jf表示。设 f : R n → R m \boldsymbol{f} \colon \mathbb{R}^n \to \mathbb{R}^m f:Rn→Rm,其对自变量 x \boldsymbol x x的梯度是一个 m × n m \times n m×n 维的矩阵:
∇ x f = ( ∇ x T f 1 ⋮ ∇ x T f m ) = ( ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n ) \nabla_{\boldsymbol x} \boldsymbol f = \begin{pmatrix} \nabla_{\boldsymbol x}^\mathrm{T} f_1 \\ \vdots \\ \nabla_{\boldsymbol x}^\mathrm{T} f_m \end{pmatrix} = \begin{pmatrix} \begin{aligned}\frac{\partial f_1}{\partial x_1}\end{aligned} & \begin{aligned}\cdots\end{aligned} & \begin{aligned}\frac{\partial f_1}{\partial x_n}\end{aligned} \\ \begin{aligned}\vdots\end{aligned} & \begin{aligned}\end{aligned} & \begin{aligned}\vdots\end{aligned} \\ \begin{aligned}\frac{\partial f_m}{\partial x_1}\end{aligned} & \begin{aligned}\cdots\end{aligned} & \begin{aligned}\frac{\partial f_m}{\partial x_n}\end{aligned} \end{pmatrix} ∇xf= ∇xTf1⋮∇xTfm = ∂x1∂f1⋮∂x1∂fm⋯⋯∂xn∂f1⋮∂xn∂fm 其中 ∇ T \nabla^\mathrm{T} ∇T表示先求梯度再转置。虽然严格意义上来说,雅可比矩阵已经不是梯度,但由于其与梯度的含义和形式都高度相似,也可以将其看作是梯度的推广。因此简单起见,统一用梯度来称呼标量值函数与向量值函数的导数,并用 ∇ \nabla ∇符号表示求梯度或雅可比矩阵。
特别的,标量值函数的梯度是向量。类比于二阶导数,如果对梯度 ∇ f \nabla f ∇f再求一次梯度,得到的矩阵就称为 f f f的黑塞矩阵(Hessian matrix):
H f = ∇ 2 f ( x ) = ( ∂ 2 f ∂ x 1 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ⋮ ⋮ ∂ 2 f ∂ x n ∂ x 1 ⋯ ∂ 2 f ∂ x n 2 ) \boldsymbol{H}_f = \nabla^2 f(\boldsymbol{x})=\begin{pmatrix} \begin{aligned}\frac{\partial^2 f}{\partial x_1^2}\end{aligned} & \begin{aligned}\cdots\end{aligned} & \begin{aligned}\frac{\partial^2 f}{\partial x_1 \partial x_n}\end{aligned} \\ \begin{aligned}\vdots\end{aligned} & \begin{aligned}\end{aligned} & \begin{aligned}\vdots\end{aligned} \\ \begin{aligned}\frac{\partial^2 f}{\partial x_n \partial x_1}\end{aligned} & \begin{aligned}\cdots\end{aligned} & \begin{aligned}\frac{\partial^2 f}{\partial x_n^2}\end{aligned} \end{pmatrix} Hf=∇2f(x)= ∂x12∂2f⋮∂xn∂x1∂2f⋯⋯∂x1∂xn∂2f⋮∂xn2∂2f
我们直接给出向量求导的一些常用公式。读者可以发现,这些公式与一元标量函数的求导并无太大差别,只是需要注意向量和矩阵的转置来使维度相符。如无特殊标明,下面所有的求导都是对向量 x \boldsymbol x x进行的。其中 a a a是标量, y \boldsymbol y y是向量, A \boldsymbol A A是矩阵。带有下角标的 α x , β x \boldsymbol\alpha_{\boldsymbol{x}}, \boldsymbol\beta_{\boldsymbol{x}} αx,βx 是 x \boldsymbol x x的向量值函数。
∇ y T x = ∇ x T y = y ∇ x T x = 2 x ∇ ∥ x ∥ 2 = x / ∥ x ∥ 2 ∇ α x T = ( ∇ x T α x ) T ∇ y T A x = A T y ∇ x T A x = ( A + A T ) x ∇ α x T β x = ( ∇ α x T ) β x + α x T ( ∇ β x ) ∇ A x = A T ∇ a x = a I \begin{aligned} & \nabla \boldsymbol y^\mathrm{T}\boldsymbol x = \nabla \boldsymbol x^\mathrm{T}\boldsymbol y = \boldsymbol y && \nabla \boldsymbol x^\mathrm{T}\boldsymbol x = 2\boldsymbol x && \nabla \lVert \boldsymbol x \lVert_2 = \boldsymbol x / \lVert \boldsymbol x \lVert_2 \\ &\nabla \boldsymbol\alpha_{\boldsymbol{x}}^\mathrm{T} = (\nabla_{\boldsymbol{x}^\mathrm{T}} \boldsymbol\alpha_{\boldsymbol{x}})^\mathrm{T} && \nabla \boldsymbol y^{\mathrm{T}}\boldsymbol A\boldsymbol x = \boldsymbol A^{\mathrm{T}}\boldsymbol y &&\nabla \boldsymbol x^{\mathrm{T}}\boldsymbol A\boldsymbol x = (\boldsymbol A + \boldsymbol A^\mathrm{T})\boldsymbol x \\ &\nabla \boldsymbol\alpha_{\boldsymbol{x}}^\mathrm{T}\boldsymbol\beta_{\boldsymbol{x}} = (\nabla\boldsymbol\alpha_{\boldsymbol{x}}^\mathrm{T}) \boldsymbol\beta_{\boldsymbol{x}} + \boldsymbol\alpha_{\boldsymbol{x}}^\mathrm{T} (\nabla \boldsymbol\beta_{\boldsymbol{x}}) && \nabla \boldsymbol A \boldsymbol x = \boldsymbol A^\mathrm{T} &&\nabla a\boldsymbol x = a \boldsymbol I \end{aligned} ∇yTx=∇xTy=y∇αxT=(∇xTαx)T∇αxTβx=(∇αxT)βx+αxT(∇βx)∇xTx=2x∇yTAx=ATy∇Ax=AT∇∥x∥2=x/∥x∥2∇xTAx=(A+AT)x∇ax=aI
与标量函数类似,函数 f ( x ) f(\boldsymbol{x}) f(x)在 x 0 \boldsymbol{x}_0 x0处取到极大值或者极小值的必要条件是在该点的梯度为零向量: ∇ f ( x ) ∣ x 0 = 0 \nabla f(\boldsymbol{x})|_{\boldsymbol{x}_0} = \boldsymbol{0} ∇f(x)∣x0=0 虽然仅有这一条件并不充分,比如图2(b)展示过的 f ( x , y ) = x 2 − y 2 f(x,y)=x^2-y^2 f(x,y)=x2−y2,其在 ( 0 , 0 ) (0,0) (0,0)处的梯度为零,但该点显然并非局部极小值。然而,进一步讨论需要用到 H f \boldsymbol H_f Hf较为复杂的性质,且梯度为零在函数光滑时是必要条件。因此,我们暂且先对梯度与极值的关系有一个基本认识,在需要深入时再具体介绍分析的方法。
四、凸函数
梯度为零并不能说明函数取到极值点。那么,是否存在一类函数,由梯度为零就可以直接推出极值点呢?考虑最简单的开口向上的二次函数 y = x 2 y=x^2 y=x2,显然函数在顶点 x = 0 x=0 x=0 处的梯度为零,同时该点也是函数的极小值点。进一步分析可以发现,在自变量 x x x由小变大的过程中,函数的导数(梯度) y ′ = 2 x y' = 2x y′=2x 是单调增加的。所以,如果导数存在零点 x 0 x_0 x0,在零点左边导数始终小于0,函数值单调减小;在零点右边导数始终大于0,函数值单调增加。这样,导数为零的点一定是函数的极小值点。
当函数的自变量由一元扩展到多元、导数扩展成梯度的时候,我们同样需要把上面的直觉扩展,找到在不同情况下都适用的描述方法。直观上来说,如果梯度为零就可以推出极小值点,函数的图像应当是没有“起伏”的,这种性质该如何描述呢?这里直接给出定义:考虑函数 f ( x ) f(\boldsymbol x) f(x),对任意 x 1 , x 2 \boldsymbol x_1, \boldsymbol x_2 x1,x2 和 0 < α < 1 0 < \alpha < 1 0<α<1,如果都有 α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≥ f ( α x 1 + ( 1 − α ) x 2 ) \alpha f(\boldsymbol x_1) + (1-\alpha)f(\boldsymbol x_2) \ge f(\alpha\boldsymbol x_1 + (1-\alpha) \boldsymbol x_2) αf(x1)+(1−α)f(x2)≥f(αx1+(1−α)x2) 就称 f f f是凸函数(convex function)。
图3是一个凸函数的示意图,我们通过这张图来简单说明凸函数定义式的几何含义。上式左边是 f ( x 1 ) f(\boldsymbol x_1) f(x1)和 f ( x 2 ) f(\boldsymbol x_2) f(x2)的加权平均,随着 α \alpha α从0变化到1,它的轨迹就是连接 ( x 1 , f ( x 1 ) ) (\boldsymbol x_1, f(\boldsymbol x_1)) (x1,f(x1))和 ( x 2 , f ( x 2 ) ) (\boldsymbol x_2, f(\boldsymbol x_2)) (x2,f(x2))两点的线段。上式右边则是 x 1 \boldsymbol x_1 x1和 x 2 \boldsymbol x_2 x2两个点先加权平均得到 α x 1 + ( 1 − α ) x 1 \alpha \boldsymbol x_1 + (1-\alpha) \boldsymbol x_1 αx1+(1−α)x1、再求函数值的结果。要让上式成立,就需要左边表示的线段始终在右边对应位置的函数值上方,和上面我们希望的函数图像没有“起伏”是一致的。否则,我们就可以在函数图像有“鼓包”的地方找到两个点,使它们的连线在函数下方了。

图4展示了常见的凸函数 f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣ 和 f ( x ) = e x f(x)=e^x f(x)=ex,以及非凸函数 f ( x ) = x 3 f(x)=x^3 f(x)=x3 和 f ( x ) = cos ( x ) , 0 ≤ x ≤ 2 π f(x)=\cos(x), 0\le x\le 2\pi f(x)=cos(x),0≤x≤2π。非凸函数的图像上还画出了一条红色虚线,表示该函数违反凸函数定义的地方。可以自行验证这些函数确实满足或不满足凸函数的定义。

从这些例子中,我们需要说明几个与上面的“直觉”不完全相同的地方,也提醒注意严谨的数学表达是比直觉更可靠的工具。第一,凸函数不一定在所有点可导(可求梯度)。例如 ∣ x ∣ |x| ∣x∣ 在 x = 0 x=0 x=0 处的梯度就不存在。但我们在机器学习中遇到的大多数函数,都可以通过合理规定不可导点的导数来尽量弥补这一缺陷,比如规定 ∣ x ∣ |x| ∣x∣ 在 x = 0 x=0 x=0 的导数为 0 0 0。第二,凸函数不一定存在极值点,例如 e x e^x ex在定义域内是单调递增函数,不存在导数为零的地方。第三,存在全局唯一极小值点的不一定是凸函数,例如 cos ( x ) \cos(x) cos(x)在 [ 0 , 2 π ] [0,2\pi] [0,2π] 区间上存在唯一极值点 x = π x=\pi x=π,且该点的导数为 − sin ( π ) = 0 -\sin(\pi)=0 −sin(π)=0。甚至 cos ( x ) \cos(x) cos(x)在极值点左边导数 − sin ( x ) -\sin(x) −sin(x) 始终为负、在极值点右边导数始终为正,与我们在本节最开始的描述相同,但它仍然不是凸函数。
与凸函数相反,如果将定义式中的 ≥ \ge ≥改为 ≤ \le ≤,即 α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≤ f ( α x 1 + ( 1 − α ) x 2 ) \alpha f(\boldsymbol x_1) + (1-\alpha)f(\boldsymbol x_2) \le f(\alpha \boldsymbol x_1 + (1-\alpha) \boldsymbol x_2) αf(x1)+(1−α)f(x2)≤f(αx1+(1−α)x2) 就得到了凹函数(concave function)。类比图2凸函数的几何解释,凹函数的图像应当是向上“鼓起”的,从而任意两点的连线都在图像的下方。因此,凸函数常常与最小化关联,凹函数常常与最大化关联。对比两者的定义式可以发现,如果 f ( x ) f(\boldsymbol x) f(x)是凸函数,那么 − f ( x ) -f(\boldsymbol x) −f(x)一定是凹函数。相应来说,最小化凸函数 f ( x ) f(\boldsymbol x) f(x)与最大化凹函数 − f ( x ) -f(\boldsymbol x) −f(x)是等价的。因此,我们只需要选取凸函数进行研究,就可以得到凹函数的所有性质。
凸函数在机器学习中非常常见,一般向量范数都是凸函数。由于凸函数的良好性质,它的优化问题通常有简单且理论上严格的解法。因此,在后续所有的模型中,我们都希望尽可能找到某种形式的凸函数作为优化问题的目标。
相关文章:

【机器学习基础】机器学习的数学基础
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

fastapi之零
FastAPI 详细介绍 FastAPI 是一个现代、快速(高性能)的 web 框架,用于构建 API。它基于标准的 Python 类型提示,使用 Starlette 作为 web 框架,Pydantic 进行数据验证和解析。以下是对 FastAPI 的详细介绍,…...

SpringBoot整合PowerJob 实现远程任务
PowerJob介绍 PowerJob 是全新一代分布式任务调度和计算框架,提供了可视化界面,可通过单机、远程等形式调用任务并提供了运行监控和日志查看的功能模块,是当前比较流行的分布式定时任务框架之一; PowerJob 官网文档地址 环境搭建…...

【扒模块】DFF
图 医学图像分割任务 代码 import torch import torch.nn as nnfrom timm.models.layers import DropPath # 论文:D-Net:具有动态特征融合的动态大核,用于体积医学图像分割(3D图像任务) # https://arxiv.org/abs/2403…...

frameworks 之Socket
frameworks 之Socket Socket服务端1.创建Socket。2.绑定socket3.监听socket4.等待客户端连接5.读取或者写入给客户端 客户端1.创建Socket。2.连接服务端Socket3.读取或者写入给客户端4.关闭socket 演示代码 Epoll创建Epoll添加或删除Epoll等待消息返回Epoll演示代码 SocketPair…...
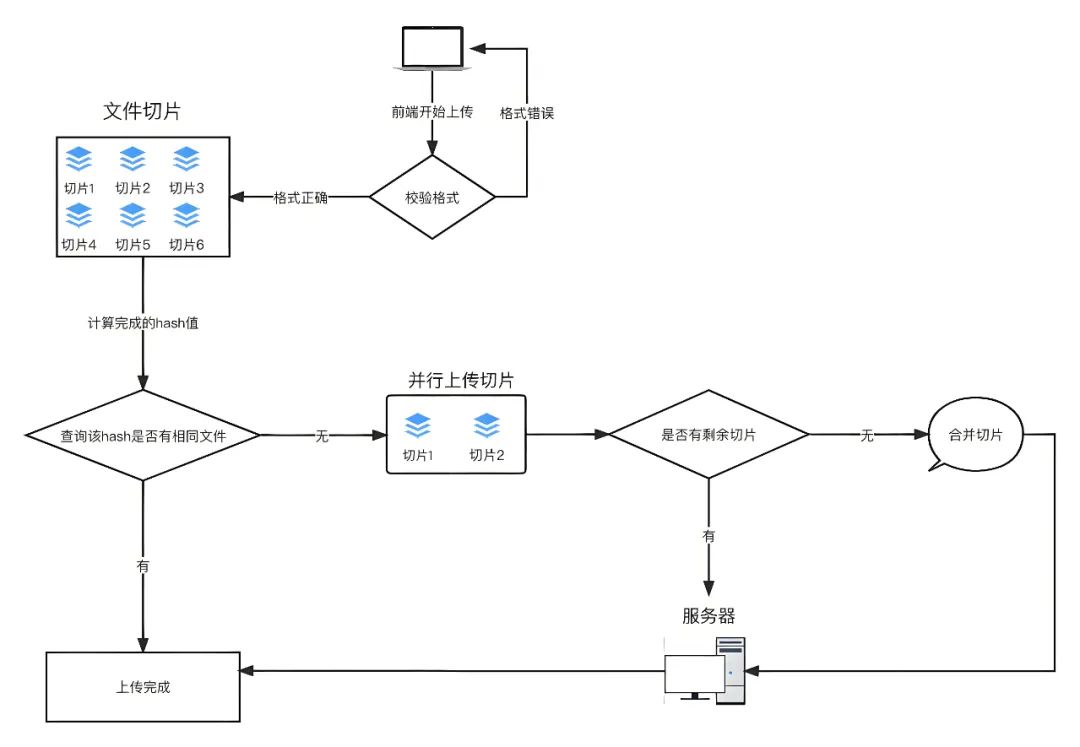
WEB前端开发中如何实现大文件上传?
大文件上传是个非常普遍的场景,在面试中也会经常被问到,大文件上传的实现思路和流程。在日常开发中,无论是云存储、视频分享平台还是企业级应用,大文件上传都是用户与服务器之间交互的重要环节。随着现代网络应用的日益复杂化&…...

ts给vue中props设置指定类型
interface IBaseObject {[key: string | number]: any; }export default defineComponent({name:xx,props:{data:{type:Object as PropType<IBaseObject>,default:()>({}),required:true},}, })...

模拟实现c++中的list模版
☺☺☺☺☺☺☺☺☺☺ 点击 进入杀马特的主页☺☺☺☺☺☺☺☺☺☺ 目录 一list简述: 二库内常用接口函数使用: 1reverse(): 2.s…...
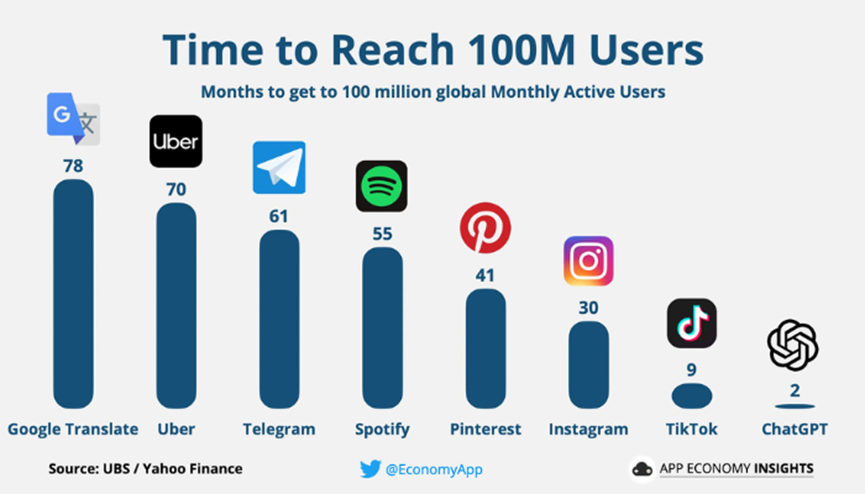
从信息论的角度看微博推荐算法
引言 在数字时代,推荐系统已成为社交媒体和其他在线服务平台的核心组成部分。它们通过分析用户行为和偏好,为用户提供个性化的内容,从而提高用户满意度和平台的参与度。推荐系统不仅能够增强用户体验,还能显著提升广告投放的效率…...
与RISC(精简指令集)的区别)
CISC(复杂指令集)与RISC(精简指令集)的区别
RISC(Reduced Instruction Set Computer)和CISC(complex instruction set computer)是当前CPU的两种架构。 它们的区别在于不同的CPU设计理念和方法。 早期的CPU全部是CISC架构,它的设计目的是要用最少的机器语言指令来完成所需的计算任务。比如对于乘法运算&#x…...

自定义数据库连接的艺术:Laravel中配置多数据库连接详解
自定义数据库连接的艺术:Laravel中配置多数据库连接详解 在现代Web应用开发中,经常需要连接到多个数据库。Laravel,作为PHP界最受欢迎的框架之一,提供了强大的数据库抽象层,支持多种数据库系统,并且允许开…...

力扣高频SQL 50题(基础版)第八题
文章目录 力扣高频SQL 50题(基础版)第八题1581. 进店却未进行过交易的顾客题目说明思路分析实现过程准备数据:实现方式:结果截图:总结: 力扣高频SQL 50题(基础版)第八题 1581. 进店…...

【C++20】从0开始自制协程库
文章目录 参考 很多人对协程的理解就是在用户态线程把CPU对线程的调度复制了一遍,减少了线程的数量,也就是说在一个线程内完成对协程的调度,不需要线程切换导致上下文切换的开销。但是线程切换是CPU行为,就算你的程序只有一个线程…...

Docker 深度解析:从入门到精通
引言 在当今的软件开发领域,容器化技术已经成为一种趋势。Docker 作为容器化技术的代表,以其轻量级、可移植性和易用性,被广泛应用于各种场景。本文将从 Docker 的基本概念入手,详细介绍 Docker 的安装、基本操作、网络配置、数据…...

[C++] 模板编程-02 类模板
一 类模板 template <class T或者typename T> class 类名 { .......... } 1.1 两种不同的实现 在以下的两种实现中,其实第一种叫做成员函数模板,并不能称为类模板因为这种实现,我们在调用时,并不需要实例化为Product这个类指定指定特定类型。 // 实现1 clas…...

嵌入式C++、STM32、树莓派4B、OpenCV、TensorFlow/Keras深度学习:基于边缘计算的实时异常行为识别
1. 项目概述 随着物联网和人工智能技术的发展,智能家居安全系统越来越受到人们的关注。本项目旨在设计并实现一套基于边缘计算的智能家居安全系统,利用STM32微控制器和树莓派等边缘设备,实时分析摄像头数据,识别异常行为(如入侵、跌倒等),并及时发出警报,提高家庭安全性。 系…...

C++ //练习 15.30 编写你自己的Basket类,用它计算上一个练习中交易记录的总价格。
C Primer(第5版) 练习 15.30 练习 15.30 编写你自己的Basket类,用它计算上一个练习中交易记录的总价格。 环境:Linux Ubuntu(云服务器) 工具:vim 代码块: /********************…...
3个方法快速找回忘记的PDF文件密码
为确保PDF文件的重要信息不轻易外泄,很多人都会给PDF文件设置打开密码,但伴随着时间的推移,让我们忘记了原本设置的密码,但这时,我们又非常急需要打开编辑这份文件,这时我们该怎么办呢?下面小编…...

排序算法:选择排序,golang实现
目录 前言 选择排序 代码示例 1. 算法包 2. 选择排序代码 3. 模拟排序 4. 运行程序 5. 从大到小排序 循环细节 外层循环 内层循环 总结 选择排序的适用场景 1. 数据规模非常小 2. 稳定性不重要 3. 几乎全部数据已排序 4. 教育目的 前言 在实际场景中…...

【测试】博客系统的测试报告
项目背景 个人博客系统采用了 SSM 框架与 Redis 缓存技术的组合 ,为用户提供了一个功能丰富、性能优越的博客平台。 在技术架构上 ,SSM 框架确保了系统的稳定性和可扩展性。Spring 负责管理项目的各种组件 ,Spring MVC 实现了清晰的请求处理…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
