规划决策算法(四)---Frenet坐标系
知乎:坐标系转换
1.Frenet 坐标系
什么是 Frenet 坐标系:
为什么使用 Frenet 坐标系: 通常情况,我们只会关注车辆当前距离左右车道线的距离,来判断是否偏离车道,是否需要打方向盘进行方向微调。而不是基于汽车的出发点,那样就太远了
往往道路是弯曲的,在直角坐标系下要计算出车辆行驶的距离要考虑道路曲率会非常麻烦。而在Frenet坐标系中,原点所在参考线与车道中心线平行,容易确定车辆偏离车道中心线的距离以及车辆沿车道中心线的行驶距离。因此使用Frenet坐标系可以忽略道路曲率的影响,让道路表达更加直观、简洁。
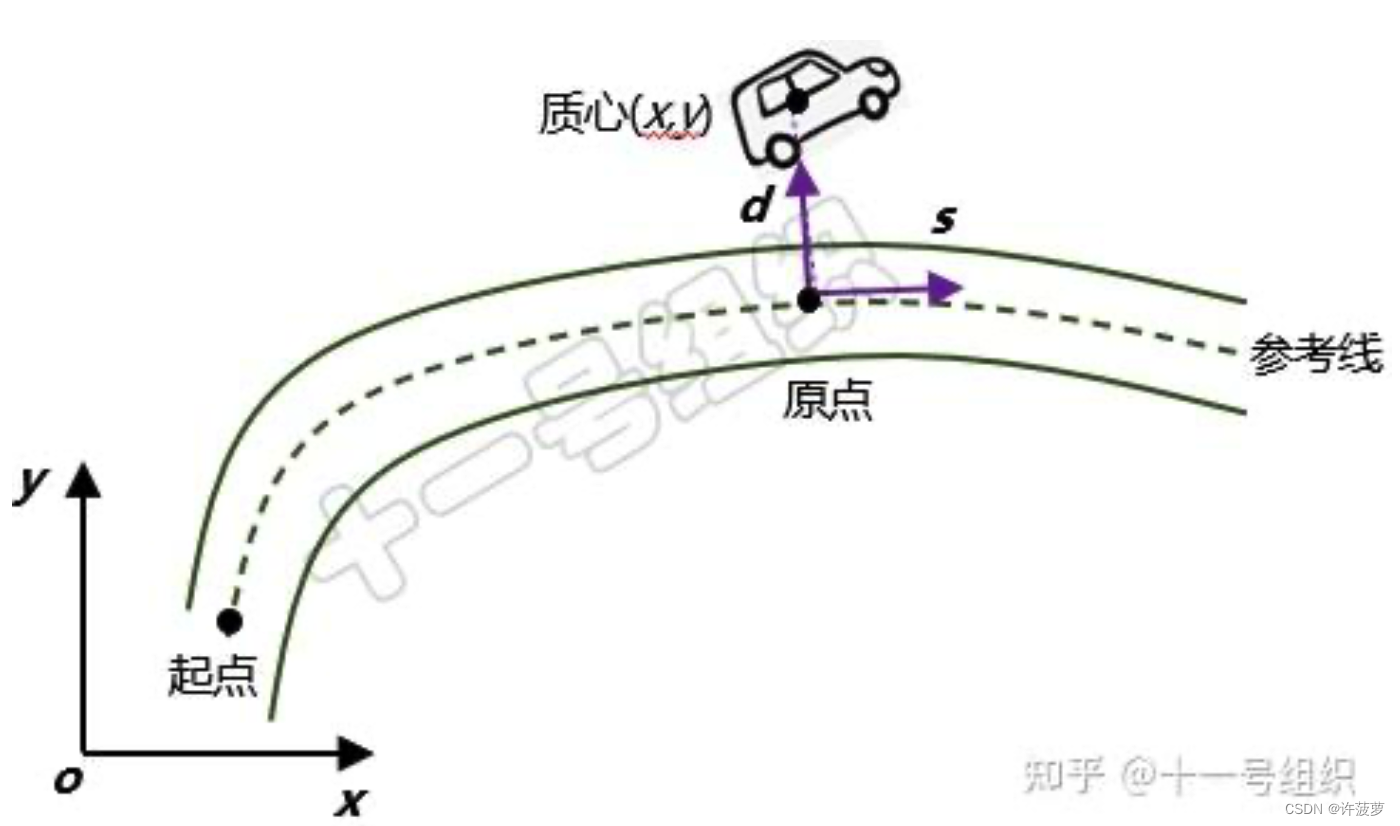


Frenet 坐标系相当于把道路抻直了
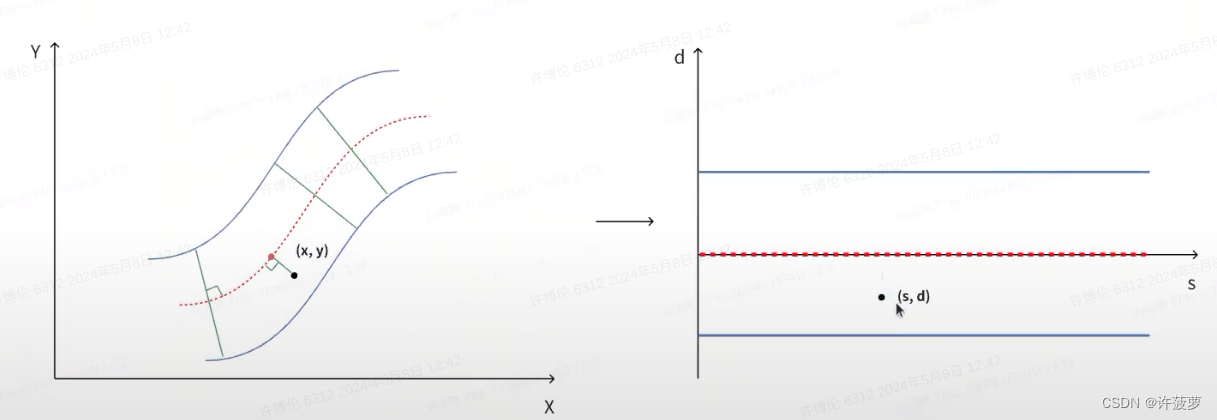
2.笛卡尔坐标系
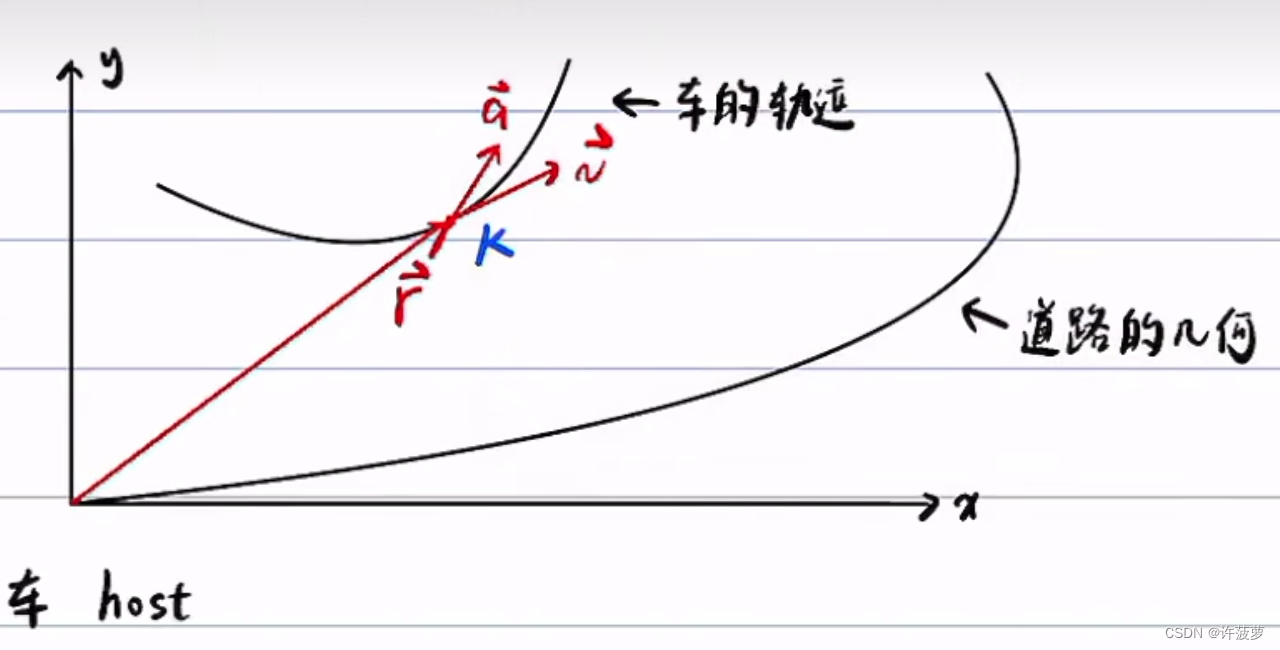

3.两者转换
在实践中只需要记住结论
推导博客
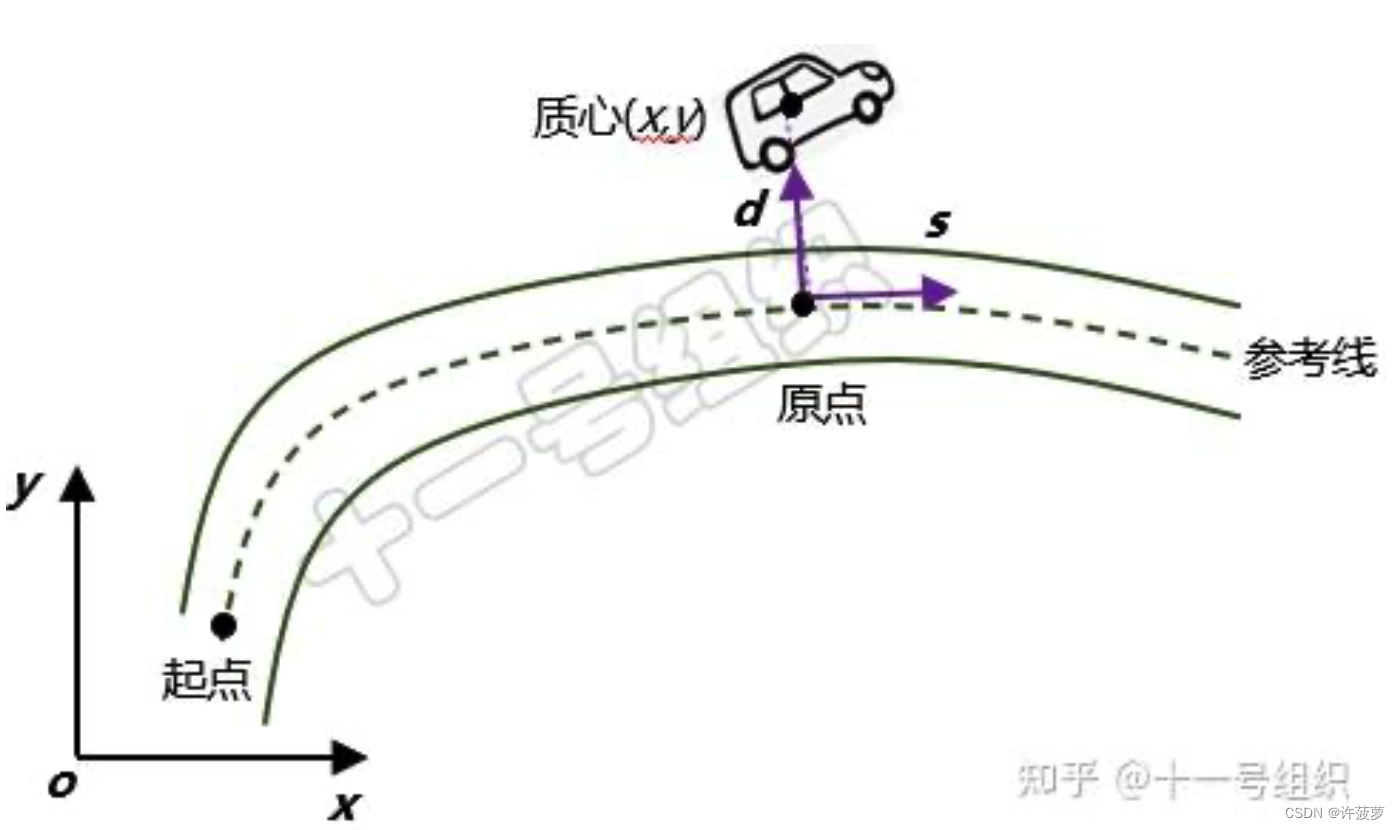
某一时刻,假设车辆质心在全局笛卡尔坐标系下的坐标为(x,y)
**原点:**车辆质心到参考线上的投影点称为
原点切线方向称为s轴方向或纵轴方向
原点法线方向称为d轴方向或横轴方向
s:值指的是参考线上的原点与起点之间曲线的长度,也就是车辆在道路上的纵向行驶距离。
d:值指的是原点与车辆质心之间的距离,也就是车辆偏离道路中心线的距离。
车辆质心随着时间在不断变化,因此Frenet坐标系的原点也在不断变换,所以Frenet坐标系是一个移动坐标系。
4.存在的问题
输入的坐标往往是笛卡尔坐标,在中间预测轨迹时使用 Frenet 坐标,最后输出给下游时还要转换成笛卡尔坐标,所以需要将 Frenet 和笛卡尔坐标之间相互转换,但是将 Frenet 坐标转为笛卡尔坐标会有以下问题

5.参考线生成
如果 Frenet 坐标建立的不够精确就会导致问题越明显,所以参考线的生成要满足一下约束,最终效果生成一条平滑的曲线 :
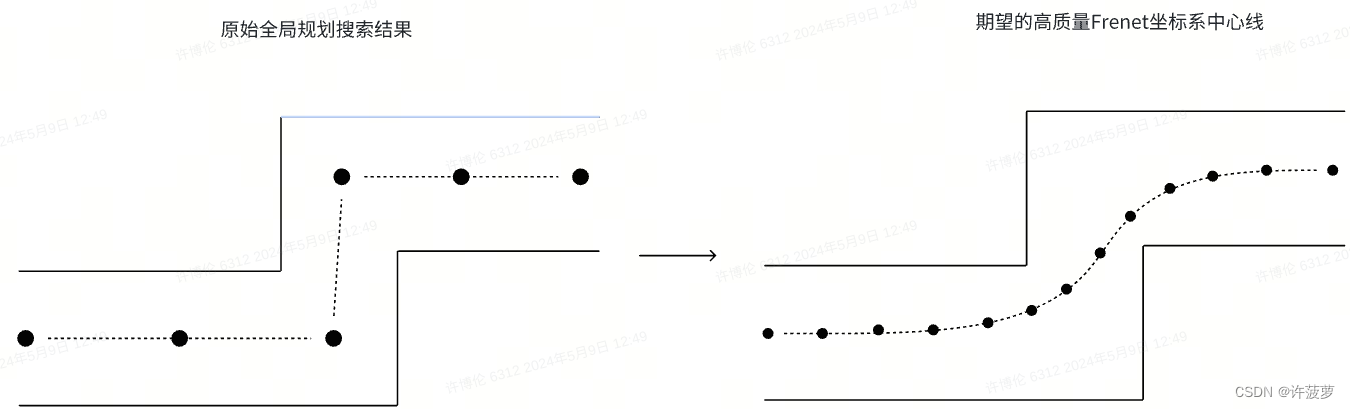
S1 :插值扩充点的个数
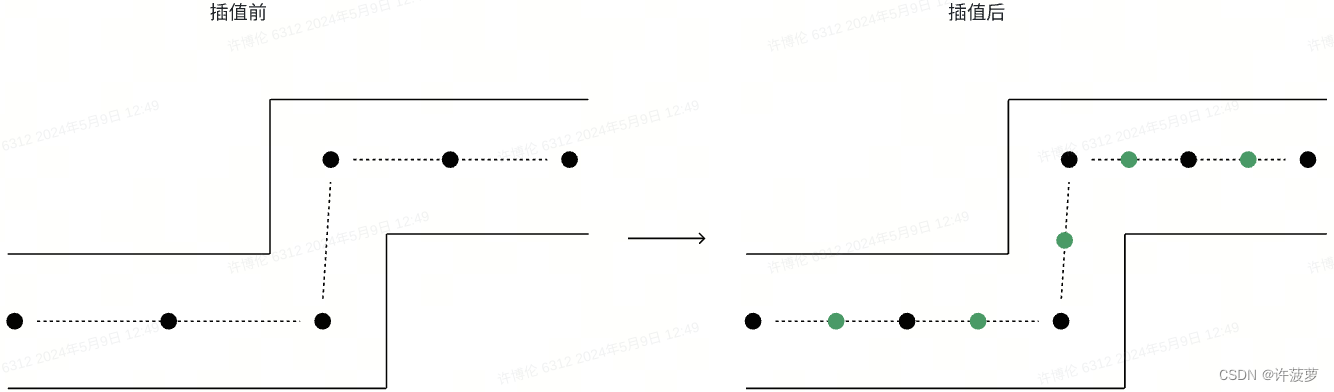
S2:将点与点之间变得平滑
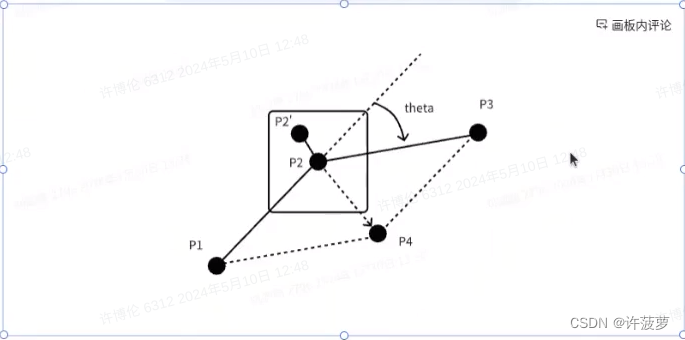
a. 考虑为了使连接成的轨迹尽可能满足平滑的要求,参考线之间应该又怎样的性质?
-
- 直线平滑度最高,自车行驶也最容易;对应图中theta越小、|P2P4|越小则越接近直线,如果 thete 很大就会是一条直线
-
- 行驶距离越短越好,所以相邻两点距离和应该越小越好 m i n ∑ ∣ ∣ P k P k − 1 ∣ ∣ 2 min\sum ||P_{k}P_{k - 1}||_{2} min∑∣∣PkPk−1∣∣2
-
- 点间距越均匀越好 m i n { a b s ( ∣ ∣ P k + 1 P k ∣ ∣ 2 − ∣ ∣ P k P k − 1 ∣ ∣ 2 ) } min\left \{ {abs(||P_{k+1}P_{k}||_{2} - ||P_{k}P_{k-1}||_{2})} \right \} min{abs(∣∣Pk+1Pk∣∣2−∣∣PkPk−1∣∣2)}
-
- 为了避免调整位置前后轨迹变化太大,应该限制每个点可以偏移原始点的位置,
同时最小化偏移距离 m i n ∑ ∣ ∣ P k P k ′ ∣ ∣ 2 min\sum ||P_{k}P_{k}{'}||_{2} min∑∣∣PkPk′∣∣2
- 为了避免调整位置前后轨迹变化太大,应该限制每个点可以偏移原始点的位置,
b. 把这个问题用数学表达式写出来:考虑上面提到的性质,把不满足上述性质的程度记作J,根据上面的描述,J应该包含下面几项,注意式中都对距离取了平方,取平方可以提升计算效率
1. 平滑代价: ∑ ∣ ∣ 2 P k − P k − 1 − P k + 1 ∣ ∣ 2 2 \sum ||2P_{k} - P_{k - 1} - P_{k + 1}||_{2}^{2} ∑∣∣2Pk−Pk−1−Pk+1∣∣22
2. 偏移代价: ∑ ∣ ∣ P k P k ′ ∣ ∣ 2 2 \sum ||P_{k}P_{k}{'}||_{2}^{2} ∑∣∣PkPk′∣∣22
3. 距离代价: ∑ ∣ ∣ P k P k − 1 ∣ ∣ 2 2 \sum ||P_{k}P_{k - 1}||_{2}^{2} ∑∣∣PkPk−1∣∣22(此部分代价同时可以反应均匀性)
c. 每个点还应该满足位置限制条件,也就是将每个点限制在框中
1. x m i n < = x k − x k ′ < = x m a x x_{min} <= x_{k} - x_{k}^{'} <= x_{max} xmin<=xk−xk′<=xmax
2. y m i n < = y k − y k ′ < = y m a x y_{min} <= y_{k} - y_{k}^{'} <= y_{max} ymin<=yk−yk′<=ymax
d. 于是,我们想让参考点变得符合我们对中心线预期的问题,就变成了下面这样一个数学问题,在满足限制条件的情况下,使得J的值最小,其中w表示各个项目的重要程度;
1. m i n { J = w 1 ∑ ∣ ∣ 2 P k − P k − 1 − P k + 1 ∣ ∣ 2 2 + w 2 ∑ ∣ ∣ P k P k ′ ∣ ∣ 2 2 + w 3 ∑ ∣ ∣ P k P k − 1 ∣ ∣ 2 2 } min\left \{ J = w_{1}\sum ||2P_{k} - P_{k - 1} - P_{k + 1}||_{2}^{2} + w_{2}\sum ||P_{k}P_{k}{'}||_{2}^{2} + w_{3}\sum ||P_{k}P_{k - 1}||_{2}^{2} \right \} min{J=w1∑∣∣2Pk−Pk−1−Pk+1∣∣22+w2∑∣∣PkPk′∣∣22+w3∑∣∣PkPk−1∣∣22}
2. s.t. x m i n < = x k − x k ′ < = x m a x x_{min} <= x_{k} - x_{k}^{'} <= x_{max} xmin<=xk−xk′<=xmax、 y m i n < = y k − y k ′ < = y m a x y_{min} <= y_{k} - y_{k}^{'} <= y_{max} ymin<=yk−yk′<=ymax
e. 问题求解,这其实是一个标准的二次规划问题,调用OSQP这个运算库就可以求解出来结果
1. 二次规划问题:目标函数是凸二次函数(最高次数为2,且为凸函数),约束条件是线性函数
2. 二次规划问题的标准形式 m i n 1 2 x T H x + q T x s . t . a T x = b h T x < = t \begin{array}{l} min\ \frac{1}{2} x^{T}Hx + q^{T}x \\ s.t.\ \ \ \ a^{T}x = b \\ \ h^{T}x <= t \end{array} min 21xTHx+qTxs.t. aTx=b hTx<=t
上方是问题的形式,下方的问题的约束
6.Frnet 坐标转笛卡尔坐标
龙格现象:
虽然高次多项式会拟合出一条更精确的曲线,但是当次数变高是会出现震荡的现象,所以我们应该使用低次多项的方式拟合一条曲线

微分基本公式及法则
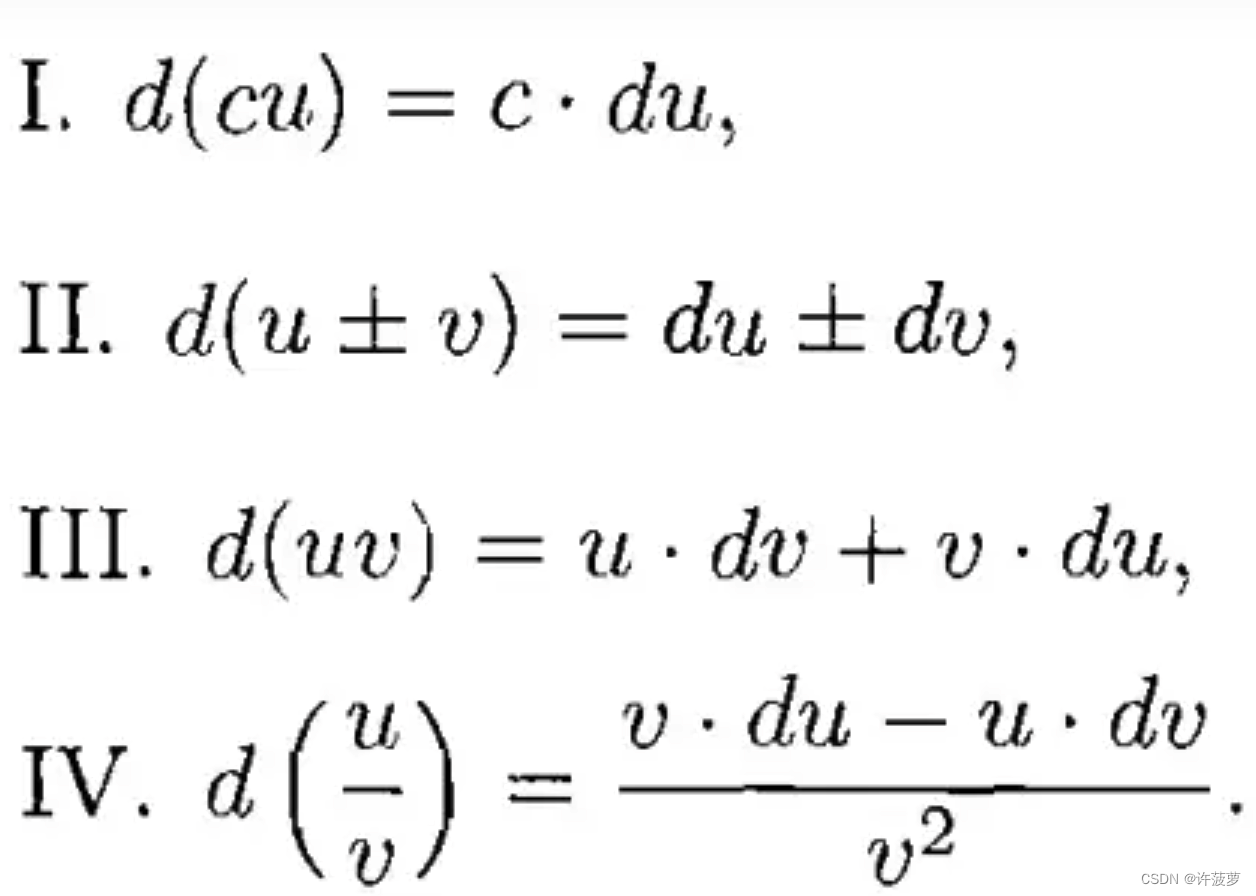
相关文章:
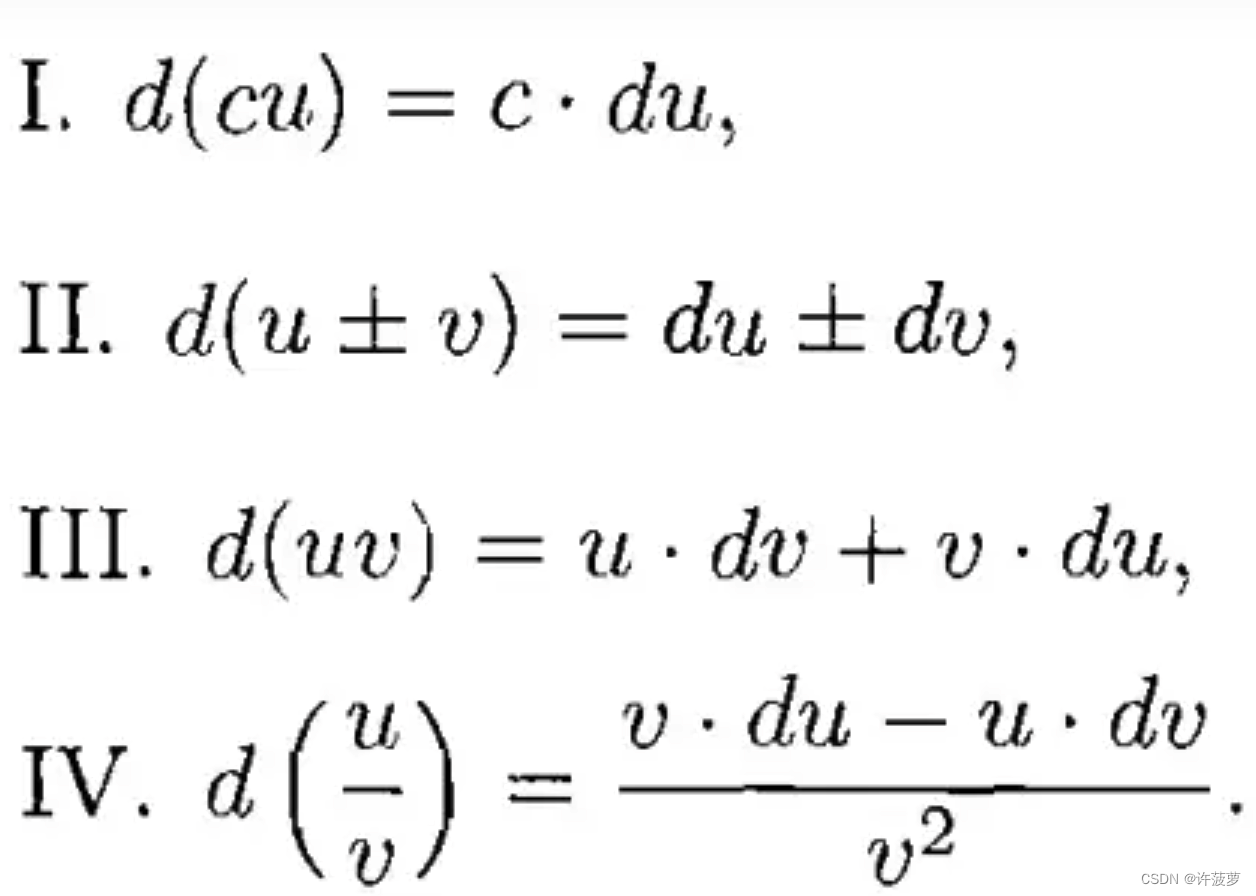
规划决策算法(四)---Frenet坐标系
知乎:坐标系转换 1.Frenet 坐标系 什么是 Frenet 坐标系: 为什么使用 Frenet 坐标系: 通常情况,我们只会关注车辆当前距离左右车道线的距离,来判断是否偏离车道,是否需要打方向盘进行方向微调。而不是基于…...

大数据处理:大数据处理框架Hadoop、Spark
大数据处理是当代信息技术领域的一个重要分支,它涉及到海量数据的存储、管理和分析。为了高效地应对大数据处理的挑战,多种框架被开发出来,其中Hadoop和Spark是最为知名和广泛应用的两种。以下将详细介绍这两种框架以及它们在大数据处理中的应…...

网传的高频流量费会影响到个人用户的算法和策略T0吗?
先解答这个问题:高频的流量费这个确实是会影响你自己算法的交易的!但是,强调一个但是:有的券商是没有流量费的!小编今天就来带大家了解一下!第一:算法交易的应用场景! 算法交易的主…...

阿里云服务器 Ubuntu18.04 安装 mysql8.0并允许外部连接
参考教程: 官网教程 参考教程一 首先彻底删除mysql5.7 dpkg --list|grep mysql #查看 sudo apt-get remove mysql-common #卸载 sudo apt-get autoremove --purge mysql-server-5.7 #版本自己修改 dpkg -l|grep ^rc|awk {print$2}|sudo xargs dpkg -P #清除残留数…...

(Arxiv-2023)MobileDiffusion:移动设备上即时文本到图像生成
MobileDiffusion:移动设备上即时文本到图像生成 Paper Title:MobileDiffusion: Instant Text-to-Image Generation on Mobile Devices Paper是谷歌出品 Paper地址 图 1:MobileDiffusion 用于 (a) 文本到图像的生成。(b) Canny 边缘到图像、风…...
【七】Hadoop3.3.4基于ubuntu24的分布式集群安装
文章目录 1. 下载和准备工作1.1 安装包下载1.2 前提条件 2. 安装过程STEP 1: 解压并配置Hadoop选择环境变量添加位置的原则检查环境变量是否生效 STEP 2: 配置Hadoop2.1. 修改core-site.xml2.2. 修改hdfs-site.xml2.3. 修改mapred-site.xml2.4. 修改yarn-site.xml2.5. 修改hado…...

【Rust光年纪】深入了解Rust语言的关键库:功能特点与使用场景分析
探索Rust语言下的重要库:硬件接口控制和数据库操作全解析 前言 随着Rust语言在嵌入式开发和数据库操作领域的不断发展,越来越多的优秀库和工具涌现出来。本文将介绍一些用于Rust语言的重要库,包括硬件接口库、嵌入式硬件抽象层、ORM和查询构…...

矩估计与最大似然估计的通俗理解
点估计与区间估计 矩估计与最大似然估计都属于点估计,也就是估计出来的结果是一个具体的值。对比区间估计,通过样本得出的估计值是一个范围区间。例如估计馒头店每天卖出的馒头个数,点估计就是最终直接估计每天卖出10个,而区间估…...

性能调优本质:如何精准定位瓶颈并实现系统极致优化
目录 先入为主的反例 性能调优的本质 性能调优实操案例 性能调优相关文章 先入为主的反例 在典型的 ETL 场景中,我们经常需要对数据进行各式各样的转换,有的时候,因为业务需求太复杂,我们往往还需要自定义 UDF(User Defined Functions)来实现特定的转换逻辑。 但是…...

Git的命令
git add . 添加到暂存区 git commit -m 备注 提交 git branch 查看所有分支 git branch -d 分支名 删除分支 git push origin --delete 分支名 远程分支删除 git branch -a 查看删除后的分支 git clone 地址 例如https://gitee.com/whale456/demo.git git push origin m…...

WPF中使用定时器更新元素-DispatcherTimer
在WPF中使用定时器来更新UI元素是一种常见且有用的做法,特别是当你需要基于时间间隔来刷新数据或执行某些操作时。DispatcherTimer是WPF中用于在UI线程上执行周期性任务的理想选择,因为它确保了对UI元素的更新是线程安全的 例子程序 每隔0.5s 界面中的…...

计算机网络 - 理解HTTP与HTTPS协议的关键区别与安全性
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有疑问和建议,请私信或评论留言! 前言 在今天的互联网…...

【Spring Framework】使用XML配置文件配置Bean的实例化方式
在 Spring Framework 中,实例化 bean 的方式非常灵活,允许开发人员根据需求选择不同的方法。以下是几种常见的实例化 bean 的方式及其示例: 1. 通过无参构造函数实例化 这是最常见的方式,Spring 会使用 bean 的默认无参构造函数…...

模拟电子技术-实验四 二极管电路仿真
实验四 二极管电路仿真 一.实验类型 验证性实验 二.实验目的 1、验证二极管的单向导电性 2、验证二极管的稳压特性。 三.实验原理 二极管的单向导电性: 四、实验内容 1、二极管参数测试仿真实验 1)仪表仿真…...
学习)
Git 子仓(Git Submodule)学习
Git 子仓学习 Git 子仓(Submodule)是 Git 提供的一种功能,用于在一个 Git 仓库(称为主仓库或 superproject)中嵌入另一个 Git 仓库(称为子仓或 submodule)。这种功能在管理大型项目或依赖关系较…...

JavaSE基础 (认识String类)
一,什么是String类 在C语言中已经涉及到字符串了,但是在C语言中要表示字符串只能使用字符数组或者字符指针,可以使用标准库提 供的字符串系列函数完成大部分操作,但是这种将数据和操作数据方法分离开的方式不符合面相对象的思想&…...

学习大数据DAY25 Shell脚本的书写2与Shell工具的使用
目录 自定义函数 递归-自己调用自己 上机练习 12 Shell 工具 sort sed awk 上机练习 13 自定义函数 name(){ action; } function name { Action; } name 因为 shell 脚本是从上到下逐行运行,不会像其它语言一样先编译,所以函数必 须在调…...

Java学习Day19:基础篇9
包 final 权限修饰符 空着不写是default! 代码块 1.静态代码块 1.静态代码块优于空参构造方法 2.静态调用只被加载一次; 静态代码块在Java中是一个重要的特性,它主要用于类的初始化操作,并且随着类的加载而执行,且只…...

如何撤销git add ,git commit 的提交记录
一、撤销git commit ,但是没有push到远程的记录 git reset --hard HEAD~1 销最近的一次提交,并且丢弃所有未提交的更改 二、撤销git add ,但是没有提交到本地仓库的记录 git reset 三、原理 Git 工作流程的简要说明: 工作目录(Working …...

Postman环境变量的高级应用:复杂条件逻辑的实现
Postman环境变量的高级应用:复杂条件逻辑的实现 在Postman中,环境变量是管理和定制API请求的强大工具。通过使用环境变量,可以轻松地在不同环境之间切换,如开发、测试和生产环境。然而,环境变量的真正威力在于它们能够…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
