《LeetCode热题100》---<5.普通数组篇六道>
本篇博客讲解LeetCode热题100道普通数组篇中的六道题
第一道:最大子数组和(中等)
第二道:合并区间(中等)
第一道:最大子数组和(中等)

法一:贪心算法

class Solution {public int maxSubArray(int[] nums) {int len = nums.length;int cur_sum = nums[0];int max_sum = cur_sum;for(int i = 1; i <len; i++){cur_sum = Math.max(nums[i],cur_sum+nums[i]);max_sum = Math.max(cur_sum,max_sum);}return max_sum;}
}1.将当前和与最大和设置为数组第一个元素
2.从第二个元素开始遍历数组元素。
- 令当前和等于 当前元素 和 当前和+当前元素 的最大值
- 令最大和等于 当前和 与 最大和 的最大值
3.返回最大和,即为答案。
法二:动态规划
class Solution {public int maxSubArray(int[] nums) {int pre = 0, maxAns = nums[0];for (int x : nums) {pre = Math.max(pre + x, x);maxAns = Math.max(maxAns, pre);}return maxAns;}
}
这个动态规划的答案实际上和上面讲的贪心算法的答案是一样的。
第二道:合并区间(中等)

方法一:排序
class Solution {public int[][] merge(int[][] intervals) {if (intervals.length == 0) {return new int[0][2];}Arrays.sort(intervals, new Comparator<int[]>() {public int compare(int[] interval1, int[] interval2) {return interval1[0] - interval2[0];}});List<int[]> merged = new ArrayList<int[]>();for (int i = 0; i < intervals.length; ++i) {int L = intervals[i][0], R = intervals[i][1];if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {merged.add(new int[]{L, R});} else {merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);}}return merged.toArray(new int[merged.size()][]);}
}
- 检查空数组:如果输入的区间数组
intervals为空,则返回一个空的二维数组。- 排序区间:将所有区间按起始位置进行排序,确保按从左到右的顺序处理区间。
- 合并区间:
- 初始化一个列表
merged,用于存储合并后的区间。- 遍历每个区间,获取当前区间的起始位置
L和结束位置R。- 如果
merged为空,或者当前区间的起始位置L大于merged中最后一个区间的结束位置,则直接将当前区间加入merged。- 否则,将当前区间与
merged中最后一个区间合并,更新最后一个区间的结束位置为二者的最大值。- 返回结果:将
merged列表转换为二维数组并返回。通过先对区间进行排序,然后逐一合并重叠区间,最终返回合并后的区间数组。
相关文章:

《LeetCode热题100》---<5.普通数组篇六道>
本篇博客讲解LeetCode热题100道普通数组篇中的六道题 第一道:最大子数组和(中等) 第二道:合并区间(中等) 第一道:最大子数组和(中等) 法一:贪心算法 class So…...

【Hot100】LeetCode—169. 多数元素
目录 题目1- 思路2- 实现⭐169. 多数元素——题解思路 3- ACM 实现 题目 原题连接:169. 多数元素 1- 思路 定义两个变量 一个是 count:维护当前元素的出现次数一个是 ret :维护当前元素 思路 遍历整个数组**①如果 count 0 **ÿ…...

专科、本科、研究生是按照什么分类的?
高等教育按照阶段主要分为以下几类 一、专业学位教育 特点:职业导向 专业学位教育是针对特定职业领域的专业培训,如医学、法律、工程等,旨在使学生具备从事相关职业所需的专业知识和实践技能。 实践性 专业学位教育注重实践教学和职业技…...

关于实时ODS层数仓搭建的三个问题
目录 问题一:数据同步的实时性无法满足 问题二:批量数据同步计算处理效率低 问题三:没有稳定的数据传输管道 FineDataLink的解决方案 实战案例-销售部门与财务部门数据同步 设置ODS层实时同步任务 设置DW层增量数据同步 设置 DM 层任务汇总 关…...

微信仿H5支付是什么
仿H5支付是指一种模拟原生H5支付流程的非官方支付方式。这种支付方式通常是由第三方支付服务提供商开发和维护的,目的是为了绕过官方支付渠道的限制,如费率、审核等问题。然而,由于仿H5支付并非官方授权和认可的支付方式,其安全性…...

网络安全知识竞赛规则及流程方案
为普及网络安全知识,进一步提升网络安全意识,树立正确的网络安全观,营造安全健康文明的网络环境,在2023年国家网络安全宣传周到来之际,特举办网络安全知识有奖竞赛活动,通过竞赛活动普及国家法律法规、政策…...

赞!蚓链用数字化打造助农扶农电商平台!
助农扶农电商平台在推动农村经济发展、促进农民增收方面发挥着重要作用。蚓链数字化平台使用“防伪溯源”为农户、商户、平台、政府与消费者打造了全方位的信任链条和纽带。给各方带来众多价值! (一)农户方面 1、拓宽销售渠道,降…...

RocketMQ延时消息
RocketMQ消息发送基本示例(推送消费者)-CSDN博客 RocketMQ消费者主动拉取消息示例-CSDN博客 RocketMQ顺序消息-CSDN博客 RocketMQ广播消息-CSDN博客 延时消息: 延时消息实现的效果就是产者调用 producer.send 方法后,消息会立即发送到 Broker,并被存…...

【C++/STL】:哈希的应用 -- 位图布隆过滤器
目录 🚀🚀前言一,位图1. 位图的概念2. STL库中的位图3. 位图的设计4. 位图的模拟实现5. 位图的优缺点6. 位图相关考察题⽬ 二,布隆过滤器1. 布隆过滤器的概念2. 布隆过滤器的实现3. 布隆过滤器删除问题4. 布隆过滤器的优缺点 点击…...
非线性面板数据实证模型及 Stata 具体操作步骤
目录 一、引言 二、文献综述 三、理论原理 四、实证模型 五、稳健性检验 六、程序代码及解释 一、引言 在当今的经济和社会研究中,非线性面板数据模型的应用日益广泛。这类模型能够更好地捕捉数据中的复杂关系,为研究者提供更深入和准确的分析结果。…...

视角 | 麻省理工学院提出出温度计校准法,专治AI大模型过度自信
在数字化浪潮的推动下,人工智能(AI)正成为塑造未来的关键力量。硅纪元视角栏目紧跟AI科技的最新发展,捕捉行业动态;提供深入的新闻解读,助您洞悉技术背后的逻辑;汇聚行业专家的见解,…...
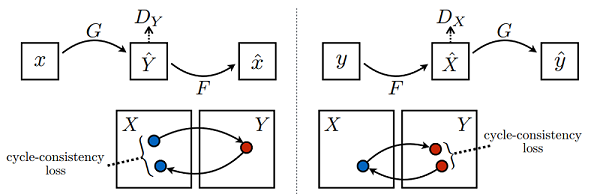
昇思25天学习打卡营第XX天|CycleGAN图像风格迁移互换
CycleGAN是一种用于图像到图像翻译的生成对抗网络,它突破了传统域迁移模型的限制,无需成对样本即可学习图像在不同域间的转换。这种无监督的方法特别适用于难以获取配对数据的场景,例如艺术风格迁移。与需要成对训练样本的Pix2Pix不同&#x…...

嵌入式Linux学习: interrupt实验
Linux中的Interrupt(中断)系统是一个至关重要的组成部分,它负责管理和处理系统中发生的各种硬件和软件中断,确保系统能够正确响应外部设备的请求,保持系统的稳定性和可靠性。 1.中断的作用 允许设备在没有CPU干预的情…...

GPT-4o mini 来袭:开发者如何驾驭新一代AI模型?
GPT-4o Mini 来袭:开发者如何驾驭新一代 AI 模型? 引言 随着人工智能(AI)技术的飞速发展,越来越多的先进模型不断涌现,给各行各业带来了深远的影响。OpenAI 最新推出的 GPT-4o Mini 是一种创新的 AI 模型…...

校园点餐系统
1 项目介绍 1.1 摘要 在这个被海量信息淹没的数字化时代,互联网技术以惊人的速度迭代,信息的触角无处不在,社会的脉动随之加速。每一天,我们都被汹涌而至的数据浪潮包裹,生活在一个全方位的数字信息矩阵中。互联网的…...

进口不锈钢309S螺栓的应用优势
进口不锈钢309S螺栓因其优异的性能和广泛的应用范围而在许多行业中备受青睐。309S不锈钢是一种含硫的易切削不锈钢,具有良好的耐高温和耐腐蚀性能,使其成为高温环境下理想的选择。下面我们就来详细探讨一下进口不锈钢309S螺栓的应用优势。 一、309S不锈钢…...

C# 设计模式之工厂方法模式
总目录 前言 本文是个人基于C#学习设计模式总结的学习笔记,希望对你有用! 在简单工厂模式中说到了简单工厂模式的缺点:简单工厂模式系统难以扩展,一旦添加新产品就不得不修改简单工厂方法,这样就会造成简单工厂的实现…...

Webpack 从入门到精通
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 一、Webpack 简介 二、Webpack 的核心概念 三、Webpack 的安装与配置 安装 Node.js 安装 Webpack 初始…...

基于VScode和C++ 实现Protobuf数据格式的通信
目录 1. Protobuf 概述1.1 定义1.2Protobuf的优势 2. Protobuf 语法3、序列号和反序列化3.1 .pb.h 头文件3.2 序列化3.3 反序列化 4、测试用例 Protobuf详细讲解链接 1. Protobuf 概述 1.1 定义 protobuf也叫protocol buffer是google 的一种数据交换的格式,它独立…...

linux环境openssl升级
1、下载openssl https://openssl-library.org/source/ 或者通过wget --no-check-certificate https://www.openssl.org/source/openssl-3.0.13.tar.gz 2、解压openssl tar -zxvf openssl-3.0.13.tar.gz 3、切换到解压后的目录 cd openssl-3.0.13/ 4、配置openssl安装目录…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
