【注意力MHA,MQA,GQA,MLA】
注意力机制优化简明图解
1. 多头注意力(MHA)
图示:
Input --> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Attention Head N]--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K , V ) \text{head}_i = \text{Attention}(Q, K, V) headi=Attention(Q,K,V)
2. 多查询注意力(MQA)
图示:
Input --> [Shared Keys & Values]--> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K shared , V shared ) \text{head}_i = \text{Attention}(Q, K_{\text{shared}}, V_{\text{shared}}) headi=Attention(Q,Kshared,Vshared)
3. 分组查询注意力(GQA)
图示:
Input --> [Attention Group 1]--> [Attention Group 2]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( group 1 , group 2 , … , group M ) \text{Output} = \text{Concat}(\text{group}_1, \text{group}_2, \ldots, \text{group}_M) Output=Concat(group1,group2,…,groupM)
group j = Attention ( Q group j , K group j , V group j ) \text{group}_j = \text{Attention}(Q_{\text{group}_j}, K_{\text{group}_j}, V_{\text{group}_j}) groupj=Attention(Qgroupj,Kgroupj,Vgroupj)
4. 多头潜在注意力(MLA)
图示:
Input --> [Compressed Keys & Values]--> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K compressed , V compressed ) \text{head}_i = \text{Attention}(Q, K_{\text{compressed}}, V_{\text{compressed}}) headi=Attention(Q,Kcompressed,Vcompressed)
低秩键值联合压缩公式:
K compressed = U K ⋅ S K ⋅ V K T K_{\text{compressed}} = U_K \cdot S_K \cdot V_K^T Kcompressed=UK⋅SK⋅VKT
V compressed = U V ⋅ S V ⋅ V V T V_{\text{compressed}} = U_V \cdot S_V \cdot V_V^T Vcompressed=UV⋅SV⋅VVT
图示概述
- MHA: 每个头独立操作,最终结果拼接。
- MQA: 多个头共享键和值,只计算一次查询,减少计算量。
- GQA: 查询分组,每组共享键和值,进一步减少计算量。
- MLA: 键和值进行压缩,减少内存和计算需求。
这些方法通过不同的策略优化注意力机制,提高了计算效率,降低了内存消耗,使Transformer模型在实际应用中更加高效。
相关文章:

【注意力MHA,MQA,GQA,MLA】
注意力机制优化简明图解 1. 多头注意力(MHA) 图示: Input --> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Attention Head N]--> [Concatenate] --> Output公式: Outpu…...

《从零开始做个摸鱼小网站! · 序》灵感来源
序 大家好呀,我是summo,这次来写写我在上班空闲(摸鱼)的时候做的一个小网站的事。去年阿里云不是推出了个活动嘛,2核2G的云服务器一年只要99块钱,懂行的人应该知道这个价格在业界已经是非常良心了,虽然优惠只有一年&a…...

计算机基础(Windows 10+Office 2016)教程 —— 第5章 文档编辑软件Word 2016(上)
文档编辑软件Word 2016 5.1 Word 2016入门5.1.1 Word 2016 简介5.1.2 Word 2016 的启动5.1.3 Word 2016 的窗口组成5.1.4 Word 2016 的视图方式5.1.5 Word 2016 的文档操作5.1.6 Word 2016 的退出 5.2 Word 2016的文本编辑5.2.1 输入文本5.2.3 插入与删除文本5.2.4 复制与移动文…...

短视频矩阵管理系统源码:实现短视频内容全面布局
随着移动互联网的普及,短视频应用逐渐成为人们获取信息、娱乐休闲的重要途径。为了满足用户多样化需求,实现短视频内容的全面布局,短视频矩阵管理系统应运而生。本文将详细介绍短视频矩阵管理系统的源码实现,帮助您更好地理解并应…...
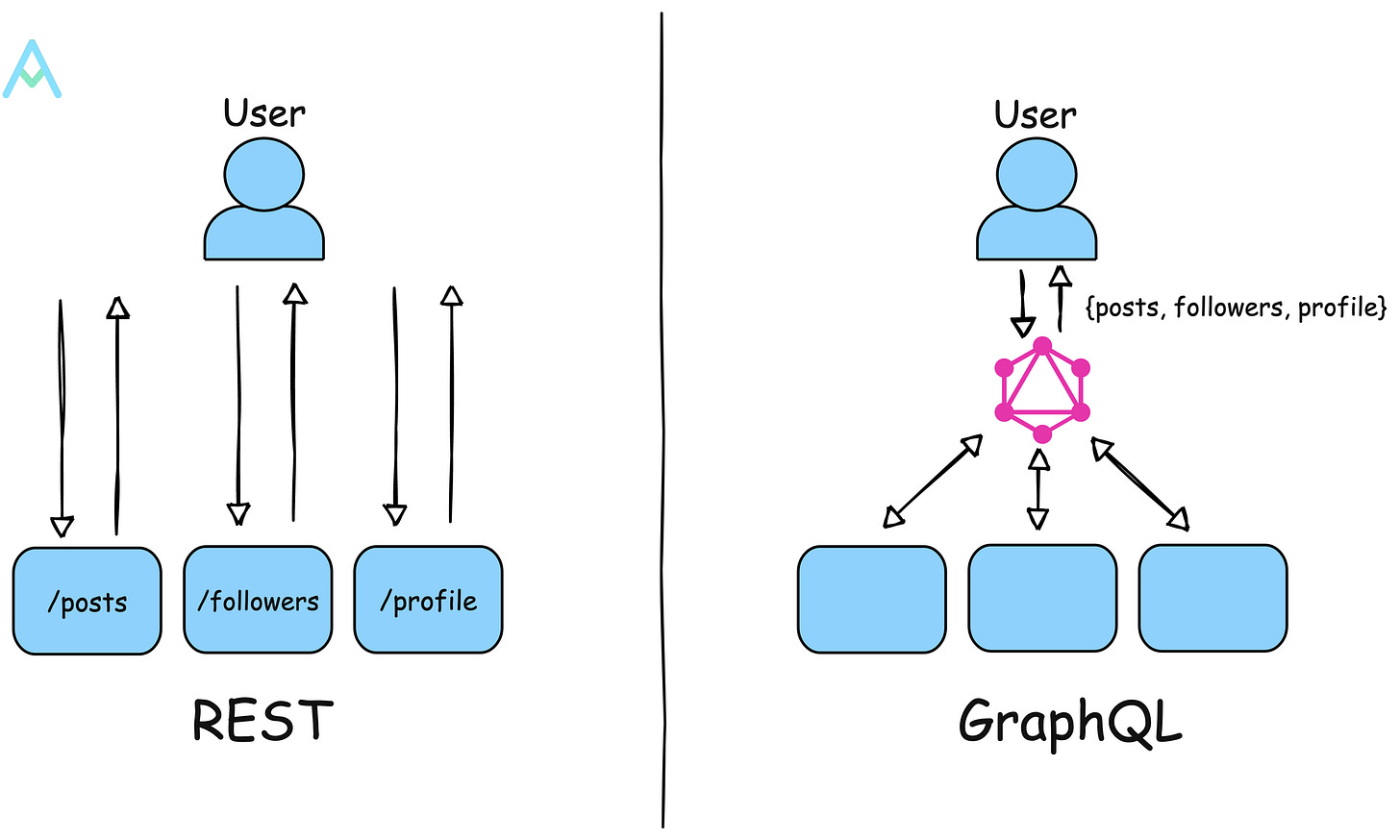
系统设计中15 个最重要的权衡
系统设计的第一法则:一切都与权衡有关。 在设计系统时,我们需要决定要包含哪些功能以及要忽略哪些功能。每次我们做这个决定时,我们都在进行权衡。在本文中,我们将探讨系统设计中遇到的15个最常见的权衡问题,并使用实…...

12年外贸实战经验,一定对你有帮助!
更多外贸干货及开发客户的方法,尽在微信【千千外贸干货】 NO1 客户总是抱怨价格太高,我常以我们产品质量过硬作为回应。但自从我进入贸易公司后,才真正意识到,在商业世界里,价格才是王道。 NO2 如果顾客提出要去工厂检…...
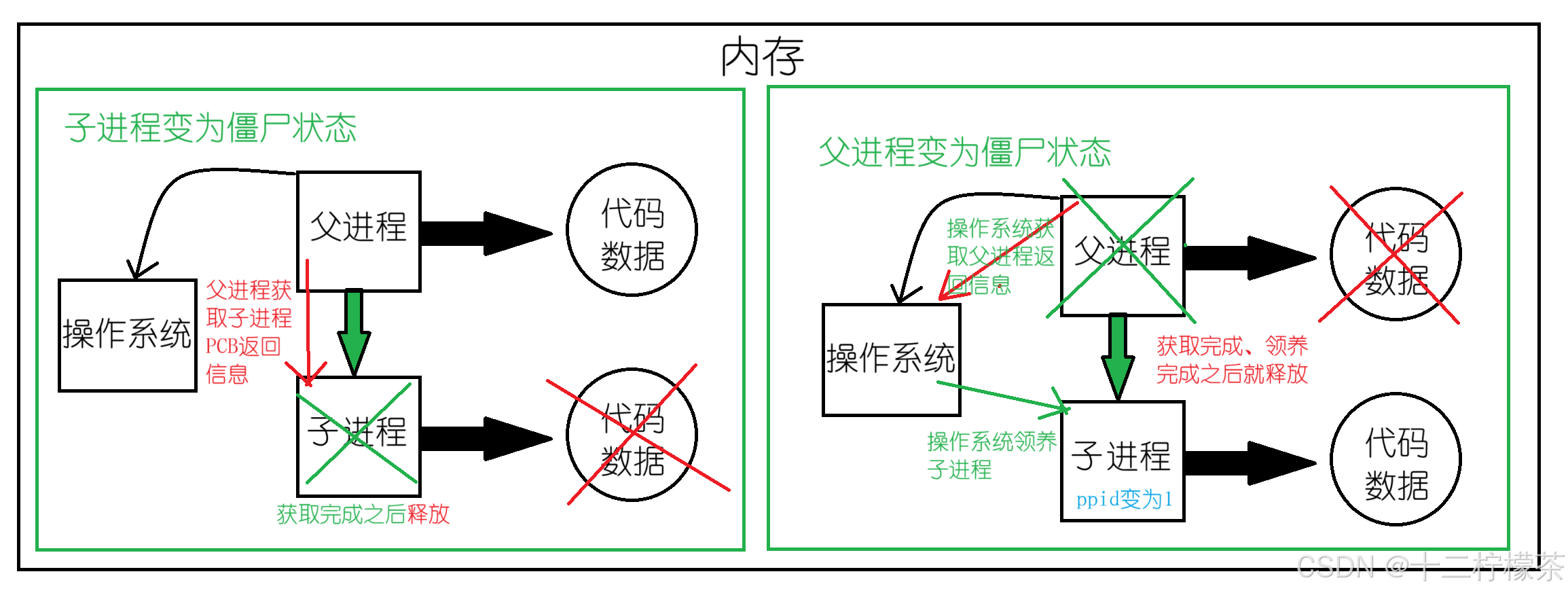
Linux---进程(3)---进程状态
目录 进程排队 进程状态 运行状态 阻塞状态 挂起状态 Linux内核具体进程状态 浅度睡眠状态 运行状态 深度睡眠状态 暂停状态 可被追踪的暂停状态 终止状态 僵尸状态 进程排队 进程不是一直在运行的,进程放在了CPU上,也不是一直运行的。 进程…...

Drools规则引擎实现停车计费
业务规则: 20:00至次日7时不收费白天7:00-20:00每小时5元,每半个小时计费一次进场30分钟内不收费,但计入时间每天最高收费50元 测试项目搭建 pom<?xml version="1.0" encoding="UTF-8"?> <project xmlns="http://maven.apache.org/POM/…...

【python虚拟环境】安装第三方包失败/failed with error code1
问题: 今天新建了一个项目,默认的虚拟环境pip包版本是19.0.3,太低了。安装第三方包的时候一直超时 解决方案: 更新pip: python -m pip install -U --force-reinstall pip然后就可以正常pip install包了 清华镜像源࿱…...

DiffusionModel-latent diffusion,VAE,U-Net,Text-encoder
Diffusers StableDdiffusion 参考: Stable Diffusion原理详解(附代码实现) Latent Diffusion 自编码器(Variational Autoencoder, VAE): 自编码器是一种无监督学习的神经网络,用于学习数据的有效表示或编码。在稳定扩…...
C# form的移植工作
前言: 目标,将一个项目的form移植到新的工程下,且能够正确编译执行: 1 Copy form的两个文件到新工程下: 比如笔者的logo form 2 修改命名空间: 然后,找到新项目的主程序: 的命名…...

linux防火墙相关命令
防火墙启动关闭 启动防火墙 systemctl start firewalld 关闭防火墙 systemctl stop firewalld 查看状态 systemctl status firewalld 开放或限制端口 开放端口 firewall-cmd --zonepublic --add-port22/tcp --permanent 重新载入一下防火墙设置,使设置生效…...

实习中学到的一点计算机知识(MP4在企业微信打不开?)
我在实习中,常有同事向我反馈说我在微信发的视频格式打不开。这就导致我还要一帧帧的盯着某一个时刻来截图,今天查了一下资料尝试修改视频后缀来解决视频的播放问题。 在网上下载mp4的格式,在本地都能播放,怎么可能发上企业微信就…...

ElasticSearch入门语法基础知识
1、创建测试索引 PUT /test_index_person {"settings": {"analysis": {"analyzer": {"ik_analyzer": {"type": "custom","tokenizer": "ik_smart"}}}},"mappings": {"proper…...
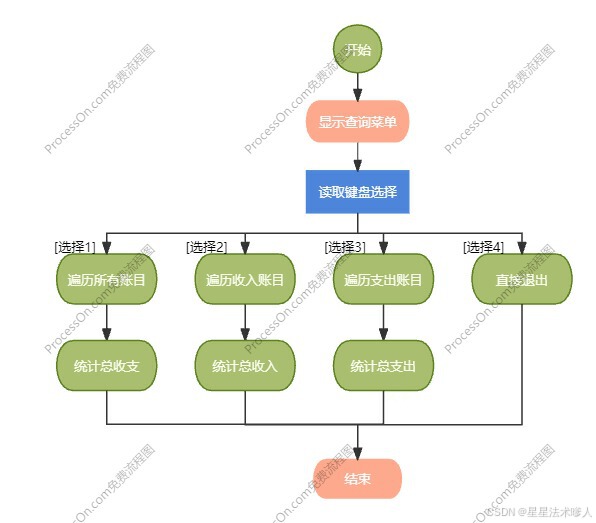
【C++】C++应用案例-dolphin海豚记账本
目录 一、整体介绍 1.1、需求和目标 1.2、整体功能描述 二、页面及功能描述 2.1 主菜单 2.2 记账菜单 2.3 查询菜单 2.4 退出功能 三、流程设计 3.1 主流程 3.2 记账操作流程 3.3 查询操作流程 四、代码设计 4.1 核心思路 4.2 项目文件分类设计 4.2.1 头文件 …...

Matlab数据处理学习笔记
1 :数据清洗 注:数据读取 (1)读取工作表 % 指定要读取的工作表 filename sales_data.xlsx; sheetName Sheet2; % 或者使用工作表编号,例如:sheetNumber 2;% 读取指定工作表的数据 data readtable(fi…...

浏览器中的同源策略、CORS 以及相关的 Fetch API 使用
前言 笔者对前端 Web 技术的认真学习,其实开始于与 Fetch API 的邂逅。当时觉得 fetch() 的设计很不错,也很希望能够请求其它网站下的数据并作处理和展示。学习过程中 HTML 和 CSS 都还好说,由于几乎没有 Web 技术的基础,学习 Fe…...
爬虫 APP 逆向 ---> 粉笔考研
环境: 粉笔考研 v6.3.15:https://www.wandoujia.com/apps/1220941/history_v6031500雷电9 模拟器:https://www.ldmnq.com/安装 magisk:https://blog.csdn.net/Ruaki/article/details/135580772安装 Dia 插件 (作用:禁…...
场 河南大学)
2024河南萌新联赛第(三)场 河南大学
B. 正则表达式 题目: https://ac.nowcoder.com/acm/contest/87865/B 给出n个地址,每个地址的形式为x.x.x.x,找四个x都满足x>0&&x<255的个数 思路: 首先定义四个数组和一个字符,然后按题目所给的形式…...

回溯法---分割回文串
题目:给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。 思路: 第一步:确定参数与返回值。参数为字符串s,分割起始下标startIndex,无返回值 第二…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
