Suno声称在受版权保护的音乐上训练模型属于“合理使用“
继美国唱片业协会(RIAA) 最近对音乐生成初创公司 Udio 和 Suno 提起诉讼之后,Suno 在周四提交的一份法庭文件中承认,该公司确实使用了受版权保护的歌曲来训练其人工智能模型。但它声称,根据合理使用原则,这样做是合法的。

美国唱片业协会于 6 月 24 日对 Udio 和 Suno 提起诉讼,指控这两家公司使用受版权保护的音乐对模特进行培训。虽然 Suno 的投资人此前曾暗示,这家初创公司没有获得音乐公司的许可使用版权材料,但并没有像今天的文件中这样直接说明。
文件指出:“Suno 的模型所训练的数以千万计的录音可能包括本案原告拥有版权的录音,这一点已不是秘密。”
Suno 首席执行官兼联合创始人米奇-舒尔曼(Mikey Shulman)在提交法律文件的同一天发表了一篇博客文章,其中继续说道:“我们根据在开放互联网上可以找到的中高品质音乐来训练我们的模型…开放互联网上的许多内容确实包含受版权保护的材料,其中一些材料为大型唱片公司所有。”
舒尔曼还认为,利用"开放互联网"上的数据训练人工智能模型,与"孩子们在听了摇滚乐之后自己创作摇滚歌曲"没有什么区别。
"学习不是侵权。过去不是,现在也不是,"舒尔曼补充道。
RIAA 对此做出了回应:“这是他们花了数月时间试图掩盖的事实的重大让步,只有在诉讼的逼迫下才承认。他们工业规模的侵权行为不属于’合理使用’。窃取艺术家毕生的心血,榨取其核心价值,并重新包装,与原创作品直接竞争,这样的行为毫无公平可言…他们对’未来音乐’的愿景显然是,歌迷将不再享受他们喜爱的艺术家的音乐,因为这些艺术家再也无法谋生。”
合理使用的问题从来都不简单,但在人工智能模型训练方面,即使是既定的理论也可能不适用。本案仍处于早期阶段,其结果很可能会开创一个有影响力的先例,而这一先例可能决定的不仅仅是本案中被点名的两家初创公司的未来。
相关文章:

Suno声称在受版权保护的音乐上训练模型属于“合理使用“
继美国唱片业协会(RIAA) 最近对音乐生成初创公司 Udio 和 Suno 提起诉讼之后,Suno 在周四提交的一份法庭文件中承认,该公司确实使用了受版权保护的歌曲来训练其人工智能模型。但它声称,根据合理使用原则,这…...

Java | Leetcode Java题解之第316题去除重复字母
题目: 题解: class Solution {public String removeDuplicateLetters(String s) {boolean[] vis new boolean[26];int[] num new int[26];for (int i 0; i < s.length(); i) {num[s.charAt(i) - a];}StringBuffer sb new StringBuffer();for (in…...
Taro学习记录
一、安装taro-cli 二、项目文件 三、项目搭建 1、Eslint配置 在项目生成的 .eslintrc 中进行配置 {"extends": ["taro/react"], //一个配置文件,可以被基础配置中的已启用的规则继承"parser": "babel/eslint-parser…...

Spring Cache框架详解
Spring Cache框架详解 Spring Cache是Spring框架提供的一个强大的缓存抽象层,旨在简化缓存技术的集成和使用。自Spring 3.1版本开始,Spring Cache就被引入以支持在Spring应用程序中添加缓存功能。随着Spring版本的迭代,Spring Cache的功能日…...

解决Html iframe 内嵌video标签导致视频无法全屏展示的问题
原因: 由于浏览器的安全策略所限制的。为了防止恶意网站利用全屏播放功能进行滥用或欺骗用户,浏览器对iframe中的视频播放做了限制。 在iframe标签中播放视频时,浏览器会根据安全策略阻止视频全屏播放。这是因为iframe标签中的内容被认为是第…...

谷粒商城实战笔记-110~114-全文检索-ElasticSearch-查询
文章目录 一,110-全文检索-ElasticSearch-进阶-两种查询方式二,111-全文检索-ElasticSearch-进阶-QueryDSL基本使用&match_all三,112-全文检索-ElasticSearch-进阶-match全文检索四,113-全文检索-ElasticSearch-进阶-match_ph…...

【开源】嵌入式Linux(IMX6U)应用层综合项目(1)--云平台调试APP
目录 1.简介 1.1功能介绍 1.2技术栈介绍 1.3演示视频 1.4硬件介绍 2.软件设计 2.1连接阿里云 2.2云平台调试UI 2.3Ui_main.c界面切换处理文件 2.4.main函数 3.结尾(附网盘链接) 1.简介 此文章并不是教程,只能当作笔者的学习分享&…...

AI人工智能分析王楚钦球拍被踩事件的真相
在2024年巴黎奥运会乒乓球混双决赛的热烈氛围中,中国队王楚钦与孙颖莎以出色的表现夺得金牌,然而,赛后发生的一起意外事件——王楚钦的球拍被踩坏,引起了广泛关注和热议。为了探寻这一事件的真相,我们可以借助AI人工智…...

C++客户端Qt开发——多线程编程(一)
多线程编程(一) ①QThread 在Qt中,多线程的处理一般是通过QThread类来实现。 QThread代表一个在应用程序中可以独立控制的线程,也可以和进程中的其他线程共享数据。 QThread对象管理程序中的一个控制线程。 run() 线程的入口…...

安装pnpm
安装pnpm(Performant npm),即高性能的npm包管理工具,可以通过多种方式进行。以下是详细的安装步骤: 一、通过npm全局安装 打开命令行工具:在你的计算机上打开命令行工具,例如Windows的CMD、Pow…...

CSS平移实现双开门效果
CSS平移实现双开门效果 一共要三张图片,一张作为父级背景,两张为兄弟左右布局 父子结构布局 一张作为父级背景,两张为兄弟左右布局。之后添加鼠标悬停效果,两张子图分别从左右平移 [外链图片转存失败,源站可能有防盗链机制,建议…...

3096. 得到更多分数的最少关卡数目
3096. 得到更多分数的最少关卡数目 题目链接:3096. 得到更多分数的最少关卡数目 代码如下: class Solution { public:int minimumLevels(vector<int>& possible) {int s0;//两个玩家能得到的分数和for(int x:possible){sx0?-1:1;}int t0;/…...
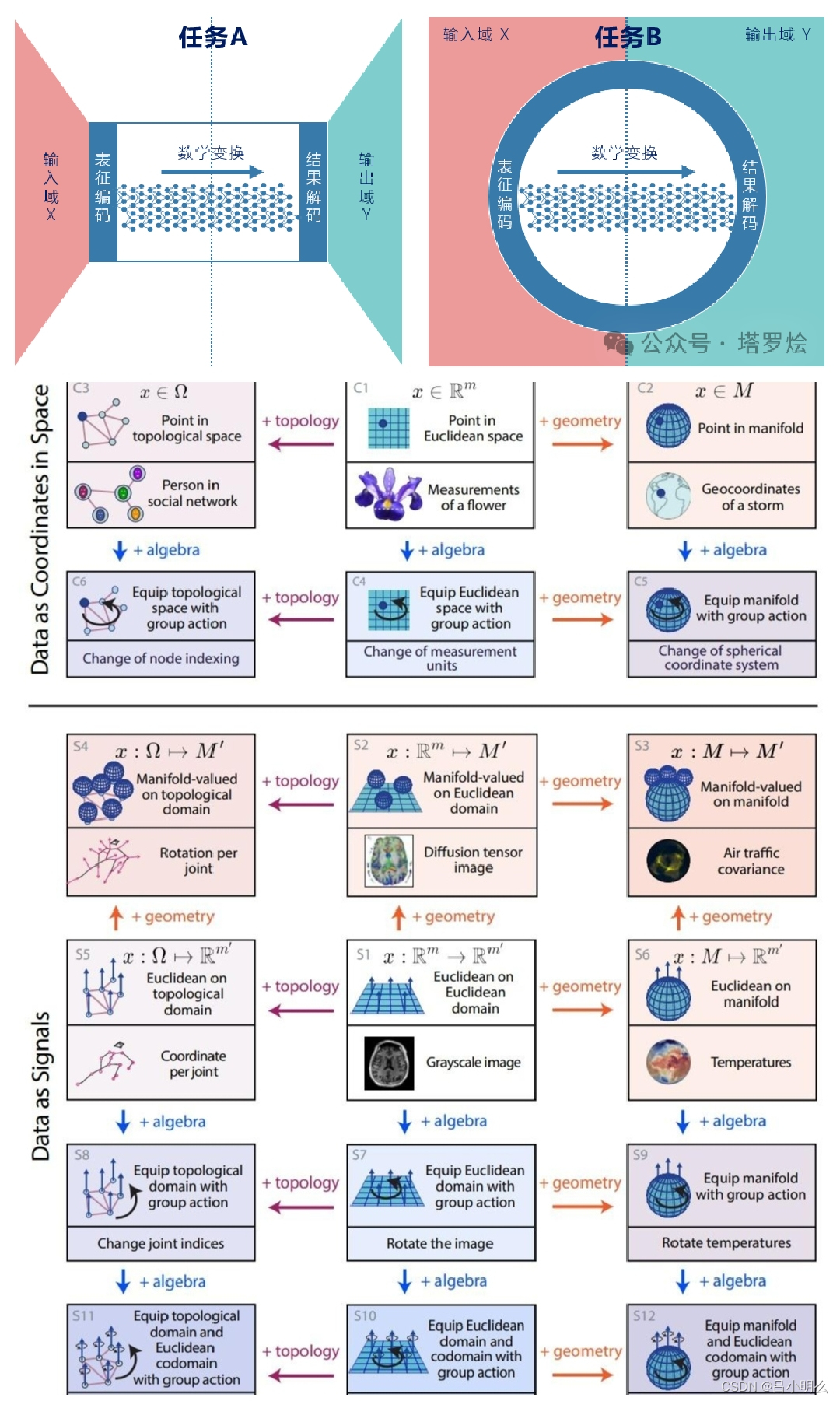
AGI思考探究的意义、价值与乐趣Ⅳ
探究in context或Prompt对于LLM来说其根本意义,in context & Prompt Learning带给我们更深一层的提示是什么? 文章里的探索希望能够将in context或Prompt置身于一个更全局的视角来看待:将其视为在真实世界中时空认知流形所映射为数据流形…...

《数据结构》(C语言版)第1章 绪论(上)
第1章 绪论 1.1 数据结构的研究内容1.2 基本概念和术语 1.1 数据结构的研究内容 N.沃思(Niklaus Wirth)教授提出: 程序算法数据结构 电子计算机的主要用途 早期:主要用于数值计算 后来:非数值计算,复杂的具有一定结构…...

【Pyhton】数据类型之详讲字符串(上)
本篇文章将详细讲解字符串: 1、定义 定义字符串时,字符串的内容被双引号,单引号,三单引号,三双引号中的其中一个被括住。 例如: 双引号: v1"haha" 单引号: v1hahah…...

算法小白的进阶之路(力扣6~8)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 非常期待和您一起在这个小…...

【期货】收盘点评。昨天说的,p2409棕榈油在今天或者周一会走出行情
收盘点评 昨天说的,p2409棕榈油在今天或者周一会走出行情。事实就是如此。震荡了几天了,波幅不大的来回震荡,其实主力是不想震荡的,但是不震荡自己的货和行情走不出来。所以我昨天就说,应该就是这一两天会走出一波小行…...

LBS 开发微课堂|Polyline绘制优化:效果更丰富,性能更佳!
为了让广大的开发者 更深入地了解 百度地图开放平台的技术能力 轻松掌握满满的技术干货 更加简单地接入 开放平台的服务 我们特别推出了 “位置服务(LBS)开发微课堂” 系列技术案例 第一期的主题是 《Polyline 绘制优化升级》 你还想了解哪些…...

VS Code设置C++编译器路径
C_Cpp.default.compilerPath是C/C编译器路径; python.condaPath是conda路径....

laravel项目配置
创建laravel项目 composer create-project --prefer-dist laravel/laravel 项目名称生成项目key php artisan key:generate.清理配置缓存 php artisan config:clearlaravel生成代码 官网链接 php artisan make:model Flight --all生成Flight类相关的文件,对应数…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
