代码随想录打卡第四十四天
代码随想录–动态规划部分
day 44 动态规划第11天
文章目录
- 代码随想录--动态规划部分
- 一、力扣1143--最长公共子序列
- 二、力扣1035--不相交的线
- 三、力扣53--最大子数组和
- 四、力扣392--判断子序列
一、力扣1143–最长公共子序列
代码随想录题目链接:代码随想录
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
思路和力扣718基本一样的,只不过是数组变成了字符串,在操作上没有区别,因为字符串也是字符的数组
定义二维的dp数组,用来记录 以text1[i-1]和text2[j-1]为结尾的最长子序列长度
但是不连续,所以要注意当text1[i-1]和text2[j-1]不相等时,dp[i][j]不能简单的赋值0,而是要取dp[i-1][j]和dp[i][j-1]的较大值
因为未来可能又有一样的值,需要在此数字基础上加一
代码如下:
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));int result = 0;for(int i = 1; i <= text1.size(); i ++)for(int j = 1; j <= text2.size(); j ++){if(text2[j-1] == text1[i-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}return dp[text1.size()][text2.size()];}
};
二、力扣1035–不相交的线
代码随想录题目链接:代码随想录
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
乍一看没什么思路,但是分析一下问题就能发现这个题是做过的
两个要求:一是元素相等,二是直线不相交
元素相等好判断,不相交怎么判断呢
实际上就是从两个数组里找到一个最长相同子序列,随意举例都没法推翻这个概念
那么就和上题一模一样了
代码如下:
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));for(int i = 1; i <= nums1.size(); i ++)for(int j = 1; j <= nums2.size(); j ++){if(nums2[j-1] == nums1[i-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}return dp[nums1.size()][nums2.size()]; }
};
三、力扣53–最大子数组和
代码随想录题目链接:代码随想录
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
定义dp数组为dp[i]代表以nums[i]为结尾的最大连续子序列和
那么递推公式应该是dp[i]=max(dp[i-1] + nums[i], nums[i])
先看一眼加上第i个会不会更大,如果还不如单独的i大,那当然是要从i重新开始计数
最后取dp的最大值即可
代码如下:
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int> dp(nums.size(), 0);dp[0] = nums[0];int result = dp[0];for(int i = 1; i < nums.size(); i ++){dp[i] = max(dp[i-1] + nums[i], nums[i]);if(dp[i] > result) result = dp[i];}return result;}
};
四、力扣392–判断子序列
代码随想录题目链接:代码随想录
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
这个题用动态规划多少有点牛刀杀鸡的感觉,其实双指针就足够了,慢指针遍历s,快指针遍历t,检查慢指针能不能到头即可
动态规划的做法需要定义二维的dp数组
dp[i][j]代表s[i-1]和t[j-1]的相同子序列长度,最后比一下是不是和s长度一样就知道了
递推公式和上面的题一样,如果s[i-1]=t[j-1],那么dp[i][j] = dp[i-1][j-1]+1,一样说明子序列多一位
不相等的话,双指针的思路是需要t往后一位,s指针不变,再搜索,这样会导致dp[i][j] = dp[i][j-1]
递推公式也明确了,就可以写了
代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size()+1, vector<int>(t.size()+1, 0));for(int i = 1; i <= s.size(); i ++)for(int j = 1; j <= t.size(); j ++){if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = dp[i][j-1];}return (dp[s.size()][t.size()] == s.size());}
};
双指针法做就是:
class Solution {
public:bool isSubsequence(string s, string t) {int slow = 0;int fast = 0;while(fast < t.size()){if(s[slow] == t[fast]){slow ++; fast++;}else fast++;}return slow == s.size();}
};
干干净净
相关文章:

代码随想录打卡第四十四天
代码随想录–动态规划部分 day 44 动态规划第11天 文章目录 代码随想录--动态规划部分一、力扣1143--最长公共子序列二、力扣1035--不相交的线三、力扣53--最大子数组和四、力扣392--判断子序列 一、力扣1143–最长公共子序列 代码随想录题目链接:代码随想录 给定…...

【JAVA】枚举类的使用:通过枚举类名称得到对应值进行输出
枚举类其实就是一个特殊的class。 /*** ClassName: CardType* Description:数字卡类型对应的文字卡类型*/ public enum CardType {NORMAL_CARD("金普卡"),BUSINESS_CARD("商务卡"),PRIVATE_CARD("黑金无限卡");private String cardName;CardTyp…...

20240731软考架构------软考6-10答案解析
每日打卡题6-10答案 6、【2012年真题】 难度:一般 若系统中的某子模块需要为其他模块提供访问不同数据库系统的功能,这些数据库系统提供的访问接口有一定的差异,但访问过程却都是相同的,例如,先连接数据库,…...

学习记录——day25 多线程编程 临界资源 临界区 竞态 线程的同步互斥机制(用于解决竟态)
目录 编辑 一、多进程与多线程对比 二、 临界资源 临界区 竞态 例1:临界资源 实现 输入输出 例2:对临界资源 进行 减减 例子3:临界资源抢占使用 三、线程的同步互斥机制(用于解决竟态) 3.1基本概念 3.2线…...

[RK3566]linux下使用upgrade_tool报错
linux下使用upgrade_tool报错Creating Comm Object failed! Rockusb>uf /home/zhuhongxi/RK3566_AOSP_SDK/rockdev/Image-rk3566_tspi/update.img Loading firmware... Support Type:RK3568 FW Ver:b.0.00 FW Time:2024-08-03 12:00:09 Loader ver:1.01 Loader Time:…...
)
系统架构师(每日一练13)
每日一练 答案与解析 1.应用系统构建中可以采用多种不同的技术,()可以将软件某种形式的描述转换为更高级的抽象表现形式,而利用这些获取的信息,()能够对现有系统进行修改或重构,从而产生系统的一个新版本。答案与解析 问题1 A.逆…...

Error: No module factory available for dependency type: CssDependency
本篇主要用来记录VUE打包的问题点,今天使用npm run build:prod 打包VUE出现如下问题: Error: No module factory available for dependency type: CssDependency 因为测试和预发布都挺正常的,正式环境竟然出问题,废话不多说&…...

【langchain学习】使用Langchain生成多视角查询
使用Langchain生成多视角查询 导入所需库: from langchain.prompts import ChatPromptTemplate from langchain_core.output_parsers import StrOutputParser from langchain_core.runnables import RunnablePassthrough from config import llm设置提示模板&#x…...

ASPCMS 漏洞详细教程
一.后台修改配置文件拿shell 登录后台 如下操作 保存并抓包 将slideTextStatus的值修改为1%25><%25Eval(Request(chr(65)))25><%25 放包(连接密码是a) 然后用工具连接 成功连接...

二维码生成原理及解码原理
☝☝☝二维码配图 二维码 二维码(Quick Response Code,简称QR码)是一种广泛使用的二维条形码技术,由日本公司Denso Wave在1994年开发。二维码能有效地存储和传递信息,广泛应用于商品追溯、支付、广告等多个领域。二维…...

云计算实训20——mysql数据库安装及应用(增、删、改、查)
一、mysql安装基本步骤 1.下载安装包 wget https://downloads.mysql.com/archives/get/p/23/file/mysql-8.0.33-1.el7.x86_64.rpm-bundle.tar 2.解压 tar -xf mysql-8.0.33-1.el7.x86_64.rpm-bundle.tar 3.卸载mariadb yum -y remove mariadb 查看解压后的包 [rootmysq…...

24年电赛——自动行驶小车(H题)基于 CCS Theia -陀螺仪 JY60 代码移植到 MSPM0G3507(附代码)
前言 只要搞懂 M0 的代码结构和 CCS 的图形化配置方法,代码移植就会变的很简单。因为本次电赛的需要,正好陀螺仪部分代码的移植是我完成的。(末尾附全部代码) 一、JY60 陀螺仪 JY60特点 1.模块集成高精度的陀螺仪、加速度计&…...

数组的增删查查改
1、增 1.Cpp #include <iostream> using namespace std; #include "add.h"int main() {//初始化数组int arr[5];//前四个元素为1,2,3,4for (int i 0; i < 4; i){arr[i] i1;}//数组第5个赋值为100arr[4] 100;for (int…...

设计模式——动态代理
设计模式——动态代理 动态代理的基本概念动态代理的实现步骤总结 在Java中,动态代理是一种强大的机制,它允许在运行时创建一个代理对象,这个代理对象可以代表另一个实际对象,它允许你在不直接操作原始对象的情况下,通…...
 的this.$notify的具体使用)
vue(element-ui组件) 的this.$notify的具体使用
getNotify() {this.noClose();let message "";message this.itemData.map((ele) > {const text "任务" ele.title "新增" ele.num "条言论";return this.$createElement("el-tooltip",{props: {content: text,pla…...

c++ - 模拟实现set、map
文章目录 前言一、set模拟实现二、map模拟实现 前言 在C标准库中,std::set 和 std::map都是非常常用的容器,它们提供了基于键值对的存储和快速查找能力。然而,关于它们的底层实现,C标准并没有强制规定具体的数据结构,只…...
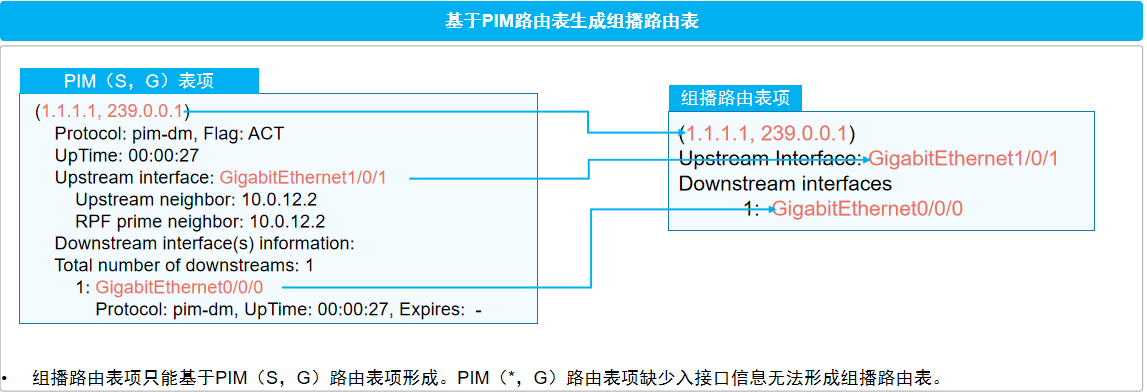
计算机网络-PIM协议基础概念
一、PIM基础概念 组播网络回顾: 组播网络从网络结构上大体可以分为三个部分: 源端网络:将组播源产生的组播数据发送至组播网络。 组播转发网络:形成无环的组播转发路径,该转发路径也被称为组播分发树(Multi…...

优化PyCharm:让IDE响应速度飞起来
优化PyCharm:让IDE响应速度飞起来 PyCharm,作为一款功能强大的集成开发环境(IDE),在提供丰富功能的同时,有时也会出现响应慢的问题。这不仅影响开发效率,还可能打击开发者的积极性。本文将详细…...

对象转化为String,String转化为对象
title: 对象转化为string,string转化为对象 date: 2024-08-02 11:50:40 tags: javascript const obj { uname:haha, age:18,gender:女} //将对象转换成string JSON.stringify(obj) //取成一个对象,将字符串传化为对象 JSON.parse(obj)常用领域在localst…...

SolverLearner:提升大模型在高度归纳推理的复杂任务性能,使其能够在较少的人为干预下自主学习和适应
SolverLearner:提升大模型在高度归纳推理的复杂任务性能,使其能够在较少的人为干预下自主学习和适应 提出背景归纳推理(Inductive Reasoning)演绎推理(Deductive Reasoning)反事实推理(Counterf…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
