java算法day28
java算法day28
- 300 最长递增子序列
- 136 只出现一次的数字
- 169 多数元素
- 234 回文链表
- 53 最大子数组和
300 最长递增子序列
这个是记忆化搜索的代码。是从递归改过来的。
这题显然是要用dp做比较合适。因为很容易看到原问题与子问题之间的关系。
还是从后往前看。
然后可以利用选与不选,或者选哪个。这两种方式来进行拆分,然后进行递归。
class Solution {int[] memo;public int lengthOfLIS(int[] nums) {if(nums==null||nums.length==0){return 0;}int n = nums.length;memo = new int[n];int maxLen = 0;for(int i = n-1;i>=0;i--){maxLen = Math.max(maxLen,dfs(nums,i));}return maxLen;}int dfs(int[] nums,int index){if(index == 0){return 1;}if(memo[index]!=0){return memo[index];}int maxLen = 1;for(int i = index-1;i>=0;i--){if(nums[i]<nums[index]){maxLen = Math.max(maxLen,dfs(nums,i)+1);}}memo[index] = maxLen;return maxLen;}}
如果你熟悉了递归转记忆化搜索转动态规划这个模式。那么可以直接来看动态规划怎么写了。
如果你懂这个过程,那么完全可以看懂递归模板这样做的原因。以及找到这些相关因素到底能有什么用。详细的总结我写在最后面那个题了。我们来看这题dp怎么做
状态定义:
dp[i]的值代表nums以nums[i]结尾的最长子序列的长度。
状态转移方程。
136 只出现一次的数字
思路:
拿到题目首先看到题目的含义,就想到了统计数字出现次数,那么就想到了Hash。但是题目不让用额外的空间,那么哈希没用了。
那么往不用空间复杂度想,我又想到了排序,但是排序最快也要o(nlogn),题目又要用o(n)时间复杂度,于是排序也没有了。
然后去看题解了。
这个解法完全是因为题目的含义才能解出来:
除了某个元素只出现一次之外,其余元素均出现2次。
这非常符合位运算的性质。你要是知道这个性质,你也可以做:
既满足时间复杂度又满足空间复杂度,就要提到位运算中的异或运算 XOR,主要因为异或运算有以下几个特点:
一个数和 0 做 XOR 运算等于本身:a⊕0 = a
一个数和其本身做 XOR 运算等于 0:a⊕a = 0
XOR 运算满足交换律和结合律:a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
由于满足交换律和结合律,那么按顺序遍历一遍进行异或运算,那么最后出现两次的肯定异或得到0了。
最后的情况肯定是这个单独的出现的元素异或0得到他本身,返回这个结果就结束了。
class Solution {public int singleNumber(int[] nums) {if(nums.length == 1){return nums[0];}int length = nums.length;//取第一个元素就开始遍历,然后返回最后的结果。int ans = nums[0];for(int i = 1;i<length;i++){ans^=nums[i];}return ans;}
}
169 多数元素
那道题想到两个想法:
1、哈希,2、排序。
class Solution {public int majorityElement(int[] nums) {Map<Integer,Integer> map = new HashMap<>();int length = nums.length;for(int i = 0;i<length;i++){if(map.containsKey(nums[i])){int value = map.get(nums[i]);map.put(nums[i],value+1);}else{map.put(nums[i],1);}}int target = length/2;for(Map.Entry<Integer,Integer> entry : map.entrySet()){int value = entry.getValue();if(value > target){return entry.getKey();}}return 0;}
}
最优解
摩尔投票
思路:
候选人candNum初始化为nums[0],票数count初始化为1。
当遇到与candNum相同的数,则票数count=count+1。
否则票数-1。
一旦count为0时,更换候选人。
遍历完数组之后,candNum即为最终答案。
原理解释:
该方法属于投票法
投票法是遇到相同的则票数+1,不同的票数-1。且众数元素的个数大于总元数的一半,其余元素的个数肯定小于一般。
因此多数元素的个数-其余元素的个数总和的结果肯定>=1。这就相当于按照这种抵消策略。最后肯定会剩余至少1个多数元素。
之前我脑子里一直有那种类似这样的例子:
1 2 1 3 1 4 1 5 。这个纯粹就是我少想了,一定是大于半数。注意是大于。所以这个思路完全行得通。
class Solution {public int majorityElement(int[] nums) {if(nums.length==1){return nums[0];}int length = nums.length;int candNum = nums[0];int count = 1;for(int i = 1;i<length;i++){if(count==0){candNum = nums[i];}if(nums[i]==candNum){count++;}else{count--;}}return candNum;}
}
234 回文链表
主要思路:
先找到中间节点:通过快慢指针,fast一次两步,slow一次一步。然后将后半段链表逆置。然后进行回文的逻辑判断即可。
关键点。其实不用考虑中间若是多一个节点的情况,多出来的那个节点完全不会比较到,因为没有比这个元素的机会,当少1个元素的链表遍历完的时候,我循环比较的逻辑就停止了。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public boolean isPalindrome(ListNode head) {if(head.next==null){return true;}ListNode fast = head;ListNode slow = head;while(fast!=null && fast.next!=null ){slow = slow.next;fast = fast.next.next;}//此时slow已经在中。然后将后面的链表逆置了ListNode pre = null;ListNode cur = slow;while(cur!=null){//存后一个节点ListNode next = cur.next;cur.next = pre;pre = cur;cur = next;}//现在来进行回文的判断ListNode l1 = head;ListNode l2 = pre;while(l1!=null && l2!=null){if(l1.val!=l2.val){return false;}l1 = l1.next;l2 = l2.next;}return true;}
}
53 最大子数组和
有了前面的积累,我终于能直接看懂动态规划的题解了。也终于知道状态转移方程怎么用了。
这里可以总结一下心路历程:
看懂动态规划之前有这样的历程:首先动态规划不是上来就有的。首先应该是暴力递归解法。将递归树画出来后,我们可以发现可以优化的点,那就是递归的过程存在很多的重复计算,那这个时候就需要“备忘录”来存储重复的计算。那么这个时候我们对这颗树做优化,你会发现这个递归树突然就变成了o(n)的量级。从递归树来看,那直接就是一路归并,值指最优值。
而这个归并正是状态转移方程。所以为什么很多题解给个初始状态,给个状态转移方程就说这个题就做完了。所以说,有时感觉这个题有很多种走法,但偏偏为什么动态规划是最优走法,就是这个原因。
本题动态规划思路:
dp[i]表示以nums[i]结尾的最大子数组和。然后一般我们从后往前思考。
分类讨论:
我把这种推导过程称之为拼与不拼。不拼那么就重起一个子数组了。
情况1:nums[i] 单独组成一个子数组,那么dp[i] = nums[i]。这种情况是纯在的,比如-1,-2,-5,7,-2,-3。那么以7这个位置为结尾的最长子数组和应该只有7本身。
情况2:将nums[i]和前面的子数组拼起来,也就是以nums[i-1]结尾的最大子数组和之和添加nums[i]。那么此时dp[i] = f[i-1]+nums[i]。
那么这个原问题和子问题的关系就很明确了。
由于每个元素都有可能是最长子数组和的结尾元素。那么可写出这个递推公式
f[i] = max(f[i-1],0) + nums[i]。
自己理解一下这个公式,这个状态转移方程的意思就是上面的两种情况。
如果f[i-1]比0还小,那说明把前面的子数组加起来是没有收益的,那么就要重起一个子数组了,此时前面这个式子值为0。此时f[i] = nums[i]。
如果你是非常清楚dp的套路。那么我告诉你一个结论,然后一个公式你应该就做完了。
1、dp[i]表示以nums[i]结尾的最长子数组的和。
2、状态转移方程:
初始状态那么就是dp[0],那么就是以nums[0]结尾的最长子数组,那么dp[0]= nums[0]。
3、循环迭代计算dp数组,然后找出以哪个为值为结尾的子数组和最大。然后返回这个最大值。
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int ans = dp[0];for(int i = 1;i<nums.length;i++){dp[i] = Math.max(dp[i-1],0) + nums[i];ans = Math.max(ans,dp[i]);}return ans;}
}
相关文章:

java算法day28
java算法day28 300 最长递增子序列136 只出现一次的数字169 多数元素234 回文链表53 最大子数组和 300 最长递增子序列 这个是记忆化搜索的代码。是从递归改过来的。 这题显然是要用dp做比较合适。因为很容易看到原问题与子问题之间的关系。 还是从后往前看。 然后可以利用选…...

vue实现歌词滚动效果
1.结构 <template><div class"lyricScroll"><div class"audio"><audio id"audio" src"./common/周传雄-青花1.mp3" controls></audio></div><div class"container" id"contai…...

【算法设计题】合并两个非递减有序链表,第1题(C/C++)
目录 第1题 合并两个非递减有序链表 得分点(必背) 题解 函数声明与初始化变量: 初始化合并链表的头节点: 合并两个链表: 处理剩余节点: 返回合并后的链表: 完整测试代码 🌈…...

Vue前端工程
创建一个工程化的vue项目 npm init vuelatest 全默认回车就好了 登录注册校验 //定义数据模型 const registerDataref({username:,password:,rePassword: }) //校验密码的函数 const checkRePassword(rule,value,callback)>{if (value){callback(new Error(请再次输入密…...

什么是药物临床试验?
药物临床试验是指在人体上进行的新药试验研究,旨在确定新药的疗效、安全性、药代动力学和药效学。临床试验不仅帮助确认药物是否对特定疾病或症状有效,还帮助识别和评估药物的副作用和风险。 药物临床试验(Clinical Trial,CT&…...

编译和汇编的区别
一、编译 编译是将高级语言(如C、C、Java等)编写的源代码转换成计算机可以直接执行的低级语言(通常是机器语言或汇编语言)的过程 编译 —— 将人类可读的源代码转换为计算机可执行的指令集 编译过程 通常包括词法分析、语法分…...

C# 设计倒计时器、串口助手开发
文章目录 1. 实现一个简单的倒计时器开始、暂停2. 串口助手开发 1. 实现一个简单的倒计时器开始、暂停 namespace Timer {public partial class Form1 : Form{int count;//用于定时器计数int time;//存储设定的定时值bool parse false;//控制暂停计时public Form1(){Initiali…...

图论① dfs | Java | LeetCode 797,Kama 98 邻接表实现(未完成)
797 所有可能路径 https://leetcode.cn/problems/all-paths-from-source-to-target/description/ 输入:graph [[1,2],[3],[3],[]] 题目分析,这里 class Solution {//这个不是二维数组,而是listList<List<Integer>> res new Ar…...

Mac安装nvm以及配置环境变量
安装nvm brew install nvm安装成功后会出现这样一段话: Add the following to your shell profile e.g. ~/.profile or ~/.zshrc:export NVM_DIR"$HOME/.nvm"[ -s "/opt/homebrew/opt/nvm/nvm.sh" ] && \. "/opt/homebrew/opt/nvm/nvm.sh&q…...

AUTOSAR实战教程-使用DET来发现开发错误
2年之前因为在调试AUTOSAR存储协议栈的时候使用DET并没发现有用的信息,所以就武断下结论--这玩意没有用。活到老学到老吧,bug经历的多了,发现这玩意还挺有用的。说一下这个bug的背景。 在将时间同步报文改道CanTsync之后,由于这个AUTOSAR工具本身的问题以及配置工程师本身的…...
:请求-响应模式,C和C++。)
ZeroMQ(二):请求-响应模式,C和C++。
目录 请求响应基础 基本概念 工作流程 典型应用 请求-响应模式的特点 应用实例 优点 缺点 ZEROMQ C语言 2.1 服务器端代码(Reply Server) 2.2 客户端代码(Request Client) 3. 编译代码 4. 详细说明 ZEROMQ C 1. …...

【虚拟仿真】Unity3D中实现2DUI显示在3D物体旁边
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 这篇文章来实现2DUI显示在3D物体旁边,当我们需要在3D模型旁边显示2DUI的时候,比如人物的对…...

代码随想录 day 29 贪心
第八章 贪心算法 part03 134. 加油站 本题有点难度,不太好想,推荐大家熟悉一下方法二 https://programmercarl.com/0134.%E5%8A%A0%E6%B2%B9%E7%AB%99.html 135. 分发糖果 本题涉及到一个思想,就是想处理好一边再处理另一边,不…...
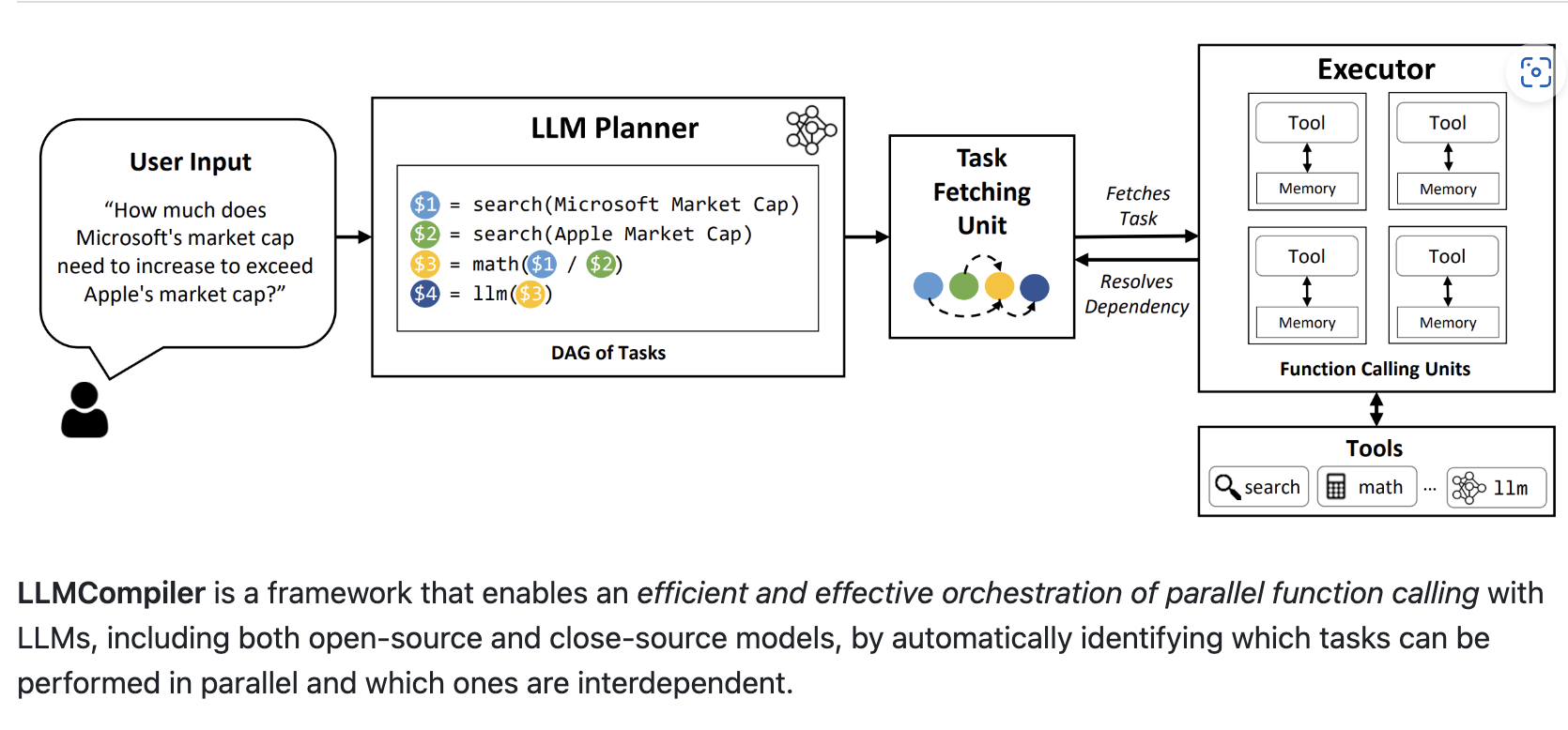
开源:LLMCompiler高性能工具调用框架
开源:LLMCompiler高性能工具调用框架 LLMCompilerLLMCompiler 框架图任务提取单元使用方式参考链接 LLMCompiler LLMCompiler 是一种 Agent 架构,旨在通过在DAG中快速执行任务来加快 Agent 任务的执行速度。它还通过减少对 LLM 的调用次数来节省 Tokens …...

【学习方法】高效学习因素 ① ( 开始学习 | 高效学习因素五大因素 | 高效学习公式 - 学习效果 = 时间 x 注意力 x 精力 x 目标 x 策略 )
文章目录 一、高效学习因素1、开始学习2、高效学习因素五大因素3、高效学习公式 - 学习效果 时间 x 注意力 x 精力 x 目标 x 策略 一、高效学习因素 1、开始学习 对于 学习差 , 调皮捣蛋 的学生 , 不要把 学习成绩差 的 原因 归因为 不爱学习 / 没有学习方法 , 可能是 还没有 …...

LeetCode Medium|【146. LRU 缓存】
力扣题目链接 题意:本题的题意就是希望我们设计一个满足 LRU 缓存的数据结构,LRU即最近最少使用。 需要我们实现 get 和 put 方法,即从缓存中获取值和设置缓存中值的方法。 还有一个约束条件就是缓存应当有容量限制,如果实现 put …...

(南京观海微电子)——LCD OTP(烧录)介绍
OTP OTP只是一种存储数据的器件,全写:ONETIMEPROGRAM。 OTP目的:提高产品的一致性 客户端的接口不支持和我们自己的产品IC之间通信,即不支持写初始化,所以产品的电学功能以及光学特性需要固化在IC中,所以需要我们来进行…...

[E二叉树] lc572. 另一棵树的子树(dfs+前中序判断+树哈希+树上KMP+好题)
文章目录 1. 题目来源2. 题目解析 1. 题目来源 链接:572. 另一棵树的子树 2. 题目解析 看到这个题目就感觉不简单,因为写了写 dfs 版本的,发现好像不太会… 还是简单粗暴一点,直接搞一个 前序中序,进行判断即可。我…...

C# 设计模式之简单工厂模式
总目录 前言 本文是个人基于C#学习设计模式总结的学习笔记,希望对你有用! 1 基本介绍 简单工厂模式 定义:用于创建对象,将对象的创建与使用分离。 简单工厂模式中用于创建实例的方法是静态(static)方法,因而简单工厂…...

mac中dyld[5999]: Library not loaded: libssl.3.dylib解决方法
需要重新安装下openssl3.0版本 brew reinstall openssl3.0 安装后执行还是报错,需要找到openssl的安装路径 /opt/homebrew/Cellar/openssl3.0/3.0.14/lib/ 将libssl.3.dylib和libcrypto.3.dylib拷贝到自己的二进制文件同目录下,再执行二进制文件就可…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
