【学习笔记】后缀自动机(SAM)
前言
之前对后缀自动机的理解太浅薄了,故打算重新写一篇。
后缀自动机是什么
后缀自动机是一个字符串的所有后缀建起来的自动机。它把所有子串(后缀的前缀)用 O ( n ) O(n) O(n) 的空间装了起来。后缀自动机的边会构成一个 D A G DAG DAG
后缀自动机的一些定义
结束位置 endpos
对于一个子串 t t t,它在原串 s s s 里面的结束位置集合记为 e n d p o s t endpos_t endpost
比如 s = a b c b c s = abcbc s=abcbc, t = b c t = bc t=bc,那么 e n d p o s t = { 2 , 4 } endpos_t = \{2,4\} endpost={2,4}(假设字符串从0开始编号)
等价类 u
所有 e n d p o s endpos endpos 相同子串是一个等价类,在后缀自动机上表现为一个点 u u u
后缀链接 link
其实就是我们常说的 f a i l fail fail
假设当前点为 u u u,设 w w w 为 e n d p o s u endpos_u endposu 中最长的字符串,那么 l i n k u link_u linku 就会连向相对于 w w w 的最长后缀的另一个 e n d p o s endpos endpos 上,一定会满足:
m i n l e n u − 1 = l e n v minlen_u-1=len_v minlenu−1=lenv
转移 nxt
同 t r i e trie trie 的转移,只不过所有的转移会构成一个 D A G DAG DAG
后缀自动机的一些性质
性质1
字符串 s s s 的两个非空子串 u u u 和 w w w(假设 ∣ u ∣ ≤ ∣ w ∣ \left|u\right|\le \left|w\right| ∣u∣≤∣w∣)的 endpos \operatorname{endpos} endpos 相同,当且仅当字符串 u u u 在 s s s 中的每次出现,都是以 w w w 后缀的形式存在的。
性质2
考虑两个非空子串 u u u 和 w w w(假设 ∣ u ∣ ≤ ∣ w ∣ \left|u\right|\le \left|w\right| ∣u∣≤∣w∣)。那么要么 endpos ( u ) ∩ endpos ( w ) = ∅ \operatorname{endpos}(u)\cap \operatorname{endpos}(w)=\varnothing endpos(u)∩endpos(w)=∅,要么 endpos ( w ) ⊆ endpos ( u ) \operatorname{endpos}(w)\subseteq \operatorname{endpos}(u) endpos(w)⊆endpos(u),取决于 u u u 是否为 w w w 的一个后缀:
{ endpos ( w ) ⊆ endpos ( u ) if u is a suffix of w endpos ( w ) ∩ endpos ( u ) = ∅ otherwise \begin{cases} \operatorname{endpos}(w) \subseteq \operatorname{endpos}(u) & \text{if } u \text{ is a suffix of } w \\ \operatorname{endpos}(w) \cap \operatorname{endpos}(u) = \varnothing & \text{otherwise} \end{cases} {endpos(w)⊆endpos(u)endpos(w)∩endpos(u)=∅if u is a suffix of wotherwise
性质3
考虑一个 endpos \operatorname{endpos} endpos 等价类,将类中的所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长,与此同时每个子串也是它前一个子串的后缀。换句话说,对于同一等价类的任一两子串,较短者为较长者的后缀,且该等价类中的子串长度恰好覆盖整个区间 [ m i n l e n , l e n ] [minlen,len] [minlen,len]。
性质4
所有后缀链接构成一棵根节点为 t 0 t_0 t0 的树(fail树)。
性质5
通过 endpos \operatorname{endpos} endpos 集合构造的树(每个子节点的 subset \textit{subset} subset 都包含在父节点的 subset \textit{subset} subset 中)与通过后缀链接 link \operatorname{link} link 构造的树相同。
性质6
对于 t 0 t_0 t0 以外的状态 v v v,可用后缀链接 link ( v ) \operatorname{link}(v) link(v) 表达 minlen ( v ) \operatorname{minlen}(v) minlen(v):
minlen ( v ) = len ( link ( v ) ) + 1. \operatorname{minlen}(v)=\operatorname{len}(\operatorname{link}(v))+1. minlen(v)=len(link(v))+1.
后缀自动机的构建
S A M SAM SAM 的构建是动态的,是在线的,每次插入一个字母。
这里先声明几个定义:
- c u r cur cur:当前节点
- l a s t last last:上一个字母代表的节点
- f a u fa_u fau:就是 l i n k u link_u linku
- n x t u [ c ] nxt_u[c] nxtu[c]:后缀自动机上的边,同 t r i e trie trie 树
- l e n u len_u lenu: e n d p o s u endpos_u endposu 中最长的字符串的长度。
下面是构建方法(假设当前字符为 c) :
- 首先我们初始化 l a s t = 1 last = 1 last=1,即 t 0 = 1 t_0=1 t0=1,代表初始节点(空字符串)
- 创建一个新状态 c u r cur cur,并令 l e n c u r = l e n l a s t + 1 len_{cur}=len_{last}+1 lencur=lenlast+1 ( l e n len len 的定义),此时 f a c u r fa_{cur} facur 无法确定,我们需要在后续的步骤确定它。
- 令 p = l a s t p = last p=last,如果 n x t p [ c ] nxt_p[c] nxtp[c] 还不存在,那么就令 n x t p [ c ] = c u r nxt_p[c] = cur nxtp[c]=cur,并让 p p p沿着 f a fa fa 往上跳,即 p = f a p p=fa_p p=fap,重复这个过程,直到 n x t p [ c ] nxt_p[c] nxtp[c] 存在或者发现这样的 p p p 不存在。
- 如果找不到合法的 p p p, p p p 就会跳到虚拟节点 0 0 0,我们令 f a c u r = 1 fa_{cur}=1 facur=1 并退出。
- 如果找到了合法的 p p p,我们记 q = n x t p [ c ] q = nxt_p[c] q=nxtp[c]
- 如果 l e n p + 1 = l e n q len_p+1=len_q lenp+1=lenq,那么可以直接令 f a c u r = q fa_{cur}=q facur=q ( l i n k link link的性质)
- 否则,就将当前状态 q q q 克隆一份,记为 r r r,并将 l e n r len_r lenr 赋值为 l e n p + 1 len_p+1 lenp+1。复制之后,我们令 f a c u r = r fa_{cur}=r facur=r。最后,从状态 p p p 开始沿着 f a fa fa 往上走,如果遇见 n x t p [ c ] = q nxt_p[c]=q nxtp[c]=q 就把它改为 r r r,否则就停下来,过程结束。
struct SAM
{int fa,len;vector<int> nxt;SAM(){fa=0; len=0;nxt.assign(27,0);}
};
vector<SAM> sam;
vector<int> dp;//这里的dp求的是 endpos 集合的 size
int last;
void insert(char c)
{int ch=c-'a';sam.push_back(SAM());int cur=sam.size()-1,p;sam[cur].len=sam[last].len+1;dp.push_back(1);for(p=last; p&&sam[p].nxt[ch]==0; p=sam[p].fa){sam[p].nxt[ch]=cur;}int q=sam[p].nxt[ch];if(q==0){sam[cur].fa=1;}else if(sam[q].len==sam[p].len+1){sam[cur].fa=q;}else{sam.push_back(SAM());int r=sam.size()-1;dp.push_back(0);sam[r]=sam[q];sam[r].len=sam[p].len+1;for(; p&&sam[p].nxt[ch]==q; p=sam[p].fa) sam[p].nxt[ch]=r;sam[cur].fa=sam[q].fa=r;}last=cur;
}//sam.assign(2,SAM());
//dp.assign(2,0);
//last=1
SAM的应用
求每个点 endpos 集合的大小
根据性质2和性质5,在 f a i l fail fail 树上,儿子是父亲的子集。所以我们可以直接在 f a i l fail fail 树上DP。
例题:P3804 【模板】后缀自动机(SAM)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+7;
struct SAM
{int fa,len;vector<int> nxt;SAM(){fa=0; len=0;nxt.assign(27,0);}
};
vector<SAM> sam;
vector<int> dp;
int last;
void insert(char c)
{int ch=c-'a';sam.push_back(SAM());int cur=sam.size()-1,p;sam[cur].len=sam[last].len+1;dp.push_back(1);for(p=last; p&&sam[p].nxt[ch]==0; p=sam[p].fa){sam[p].nxt[ch]=cur;}int q=sam[p].nxt[ch];if(q==0){sam[cur].fa=1;}else if(sam[q].len==sam[p].len+1){sam[cur].fa=q;}else{sam.push_back(SAM());int r=sam.size()-1;dp.push_back(0);sam[r]=sam[q];sam[r].len=sam[p].len+1;for(; p&&sam[p].nxt[ch]==q; p=sam[p].fa) sam[p].nxt[ch]=r;sam[cur].fa=sam[q].fa=r;}last=cur;
}
ll ans;
vector<vector<int>> e;
void dfs(int u)
{for(auto v:e[u]){dfs(v);dp[u]+=dp[v];}if(dp[u]!=1)ans=max(ans,1ll*dp[u]*sam[u].len);
}
void O_o()
{last=1;sam.assign(2,SAM());dp.assign(2,0);string s;cin>>s;for(auto c:s) insert(c);int n=sam.size()-1;e.assign(n+1,vector<int>());for(int i=1; i<=n; i++){if(sam[i].fa){e[sam[i].fa].push_back(i);}}ans=0;dfs(1);cout<<ans;
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout<<fixed<<setprecision(12);int T=1;
// cin>>T;while(T--){O_o();}
}
求不同的子串个数
一开始我们就说了个性质,你在SAM上乱走就可以走出一个子串。其实只要你走的路径不同,走出的子串一定不一样。问题就变成了从 t 0 t_0 t0 出发,总共有多少条路径。这是一个经典的 DAG 上 DP 问题。转移为
d p u = 1 + ∑ d p v dp_u=1+\sum dp_v dpu=1+∑dpv
最后要去掉空字符串的答案,也就是 d p 1 − 1 dp_1-1 dp1−1
如果是求子串个数,那就把 d p dp dp 式子换成
d p u = s i z u + ∑ d p v dp_u=siz_u+\sum dp_v dpu=sizu+∑dpv
其中 s i z u = ∣ e n d p o s u ∣ siz_u=|endpos_u| sizu=∣endposu∣ ,还是得减掉空字符串的方案。
void dfs2(int u)
{if(dp[u]) return ;for(int i=0; i<26; i++){int v=sam[u].nxt[i];if(!v) continue;dfs2(v);dp[u]+=dp[v];}dp[u]+=sum[u];
}
当然,求本质不同的字符串总数还有另一种方法:
根据性质3
a n s = ∑ l e n i − l e n f a i ans=\sum len_{i}-len_{fa_i} ans=∑leni−lenfai
//求每次插入后有多少本质不同的字符串
void insert(int ch)
{sam.push_back(SAM());int cur=sam.size()-1,p;sam[cur].len=sam[last].len+1;dp.push_back(1);for(p=last; p&&sam[p].nxt[ch]==0; p=sam[p].fa){sam[p].nxt[ch]=cur;}int q=sam[p].nxt[ch];if(q==0){sam[cur].fa=1;}else if(sam[q].len==sam[p].len+1){sam[cur].fa=q;}else{sam.push_back(SAM());int r=sam.size()-1;dp.push_back(0);sam[r]=sam[q];sam[r].len=sam[p].len+1;for(; p&&sam[p].nxt[ch]==q; p=sam[p].fa) sam[p].nxt[ch]=r;sam[cur].fa=sam[q].fa=r;}last=cur;ans+=sam[cur].len-sam[sam[cur].fa].len;cout<<ans<<"\n";
}
求第 k 小的子串
上一个问题中我们求出了从某个节点开始走一共有多少条路径,也就是从 i i i 开始一共有多少子串。这个时候就可以利用起来了。
如果你是在 t r i e trie trie 树上,怎么求排名第 k k k 的子串?——类似平衡树求第 k k k 小。
后缀自动机也一样,只不过每个点的 s i z e size size 不再是 1 1 1 了,而是 e n d p o s endpos endpos 集合大小。
只要把 trie 树上做的 − 1 -1 −1 改成 − s i z -siz −siz 即可,注意空子串还是不能算,也就是 s i z 1 = 0 siz_1=0 siz1=0。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+7,inf=1e18;
struct SAM
{int fa,len;vector<int> nxt;SAM(){fa=len=0;nxt.assign(26,0);}
};
int last=1;
vector<int> sum,dp;
vector<SAM> sam;
void insert(char c)
{int ch=c-'a';sam.push_back(SAM());int cur=sam.size()-1,p;sam[cur].len=sam[last].len+1;sum.push_back(1);for(p=last; p&&sam[p].nxt[ch]==0; p=sam[p].fa){sam[p].nxt[ch]=cur;}int q=sam[p].nxt[ch];if(!q){sam[cur].fa=1;}else if(sam[q].len==sam[p].len+1){sam[cur].fa=q;}else{sam.push_back(SAM());int r=sam.size()-1;sum.push_back(0);sam[r]=sam[q];sam[r].len=sam[p].len+1;for(; p&&sam[p].nxt[ch]==q; p=sam[p].fa){sam[p].nxt[ch]=r;}sam[q].fa=sam[cur].fa=r;}last=cur;
}
vector<vector<int>> e;
void dfs1(int u)
{for(auto v:e[u]){dfs1(v);sum[u]+=sum[v];}
}
void dfs2(int u)
{if(dp[u]) return ;for(int i=0; i<26; i++){int v=sam[u].nxt[i];if(!v) continue;dfs2(v);dp[u]+=dp[v];}dp[u]+=sum[u];
}
bool solve(int u,int k)
{k-=sum[u];if(k<=0) return 1;for(int i=0; i<26; i++){int v=sam[u].nxt[i];if(!v) continue;if(dp[v]>=k){cout<<char(i+'a');solve(v,k);return 1;}else k-=dp[v];}return 0;
}
void O_o()
{last=1;sam.assign(2,SAM());sum.assign(2,0);string s;cin>>s;for(auto c:s) insert(c);int n=sam.size()-1;dp.assign(n+1,0);int op,k;cin>>op>>k;if(op){e.assign(n+1,vector<int>());for(int i=1; i<=n; i++) if(sam[i].fa){e[sam[i].fa].push_back(i);}dfs1(1);}else{sum.assign(n+1,1);}dfs2(1);sum[1]=0;if(!solve(1,k)){cout<<"-1\n";return;}}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout<<fixed<<setprecision(12);int T=1;
// cin>>T;while(T--){O_o();}
}
最小循环位移
循环的问题一般就是把字符串复制一遍接在后面,这个也不例外。
令 s ′ = s + s s'=s+s s′=s+s,建立SAM
每次贪心的走最小的字符,走到长度为 s . s i z e ( ) s.size() s.size() 时就退出。
字符串出现次数
(kmp不香吗)
先预处理每个点 e n d p o s endpos endpos 集合大小
然后直接拿模式串在SAM上匹配,匹配成功就是 s i z siz siz,不成功就是 0 0 0
相关文章:
)
【学习笔记】后缀自动机(SAM)
前言 之前对后缀自动机的理解太浅薄了,故打算重新写一篇。 后缀自动机是什么 后缀自动机是一个字符串的所有后缀建起来的自动机。它把所有子串(后缀的前缀)用 O ( n ) O(n) O(n) 的空间装了起来。后缀自动机的边会构成一个 D A G DAG DA…...

Godot的节点与场景
要深入的理解节点与场景,我们需要跳出这两个概念来看他。说的再直白一些godot本质就是一个场景编辑器! 场景的概念应该在我们平时看电影看电视时会经常提到,比如某一个打斗的场景,这个场景可能会被设在某一个街道,那么…...
 ---- std::cout 格式化输出)
C++ 学习(2) ---- std::cout 格式化输出
目录 std::cout 格式化输出简介使用成员函数使用流操作算子 std::cout 格式化输出简介 C 通常使用cout输出数据,和printf()函数相比,cout实现格式化输出数据的方式更加多样化; 一方面,cout 作为 ostream 类的对象,该类…...
序列化一下)
前端拿不到Long类型成员变量,用@JsonSerialize(using = ToStringSerializer.class)序列化一下
EqualsAndHashCode(callSuper true) Data TableName("la_school_business") Schema(description "商务负责人表") public class SchoolBusiness extends BaseEntity {private static final long serialVersionUID -7124481085999629236L;/*** 商务负责人…...

JWT登录校验流程
jwt令牌的基本概念: 1. JWT(JSON Web Token) 定义:JWT 是一种开放标准(RFC 7519),用于在各方之间作为 JSON 对象安全地传输信息。它可以被验证和信任,因为它是数字签名的。结构&am…...

yarn安装和部署
文章目录 概述安装部署1.构建项目2.测试3.清理构建目录 小结 概述 yarn是一个快速、可靠和安全的JavaScript包管理工具,由Facebook开发。它被设计用来替代npm(Node Package Manager),尽管它与npm在很多方面兼容。yarn提供了以下一…...

Visual Studio的安装教程与使用方法
Visual Studio的安装教程与使用方法 一、Visual Studio的安装教程 1. 准备工作 确认系统要求: 在开始安装Visual Studio之前,请确保您的计算机满足Visual Studio的系统要求这。包括操作系统版本、内存、硬盘空间等。您可以在Visual Studio的官方网站…...
一键换装软件哪个好?6个换装工具让你秒变穿搭达人
#紫色跑道的city穿搭#火了,很多人都开始打卡各种紫色穿搭,展示自己的时尚态度。 但对于没有时间或金钱去精心搭配的我们来说,有没有一种更简单、更快捷的方式,让我们也能轻松跟上潮流呢? 当然有!今天&…...

【EtherCAT】Windows+Visual Studio配置SOEM主站——源码配置
目录 一、准备工作 1. Visual Studio 2022 2. Npcap 1.79 3. SOEM源码 二、源码部署 1. 新建Visual Studio工程 2. 创建文件夹 3. 创建主函数 4. 复制源代码 5. 删除无关项 6. 将soem源码添加进工程 7. 添加soem头文件 8. 配置头文件路径 9. 配置静态库和静态库路…...

GPTPDF深度解析:开源文档处理技术全攻略
GPTPDF深度解析:开源文档处理技术全攻略 在数字化信息时代,PDF文件因其稳定性和跨平台兼容性,已成为学术交流、技术文档和电子书籍等领域的首选格式。然而,PDF文档的处理和内容提取一直是一个难题。随着人工智能技术的飞速发展&a…...

网络学习:应用层DNS域名解析协议
目录 一、简介 二、工作流程 一、简介 DNS( Domain Name System)是“域名系统”的英文缩写,是一种组织成域层次结构的计算机和网络服务命名系统,它用于TCP/IP网络,它所提供的服务是用来将主机名和域名转换为IP地址的工作。 同时,DNS…...

7.怎么配置一个axios来拦截前后端请求
首先创建一个axios.js文件 导入我们所需要的依赖 import axios from "axios"; import Element from element-ui import router from "./router"; 设置请求头和它的类型和地址 注意先注释这个url,还没有解决跨域问题,不然会出现跨域 // axios.defaults.…...

Day17_1--AJAX学习之GET/POST传参
AJAX 简介 AJAX 是一种在无需重新加载整个网页的情况下,能够更新部分网页的技术。其实AJAX就可以理解为就是JS。通过AJAX也就实现了前后端分离,前端只写页面,后端生成数据! 现在开始通过实例学习: 1--GET传参 <!…...

golang国内proxy设置
go env -w GOPROXYhttps://goproxy.cn,direct经常使用的两个, goproxy.cn 和 goproxy.io 连接分别是 https://goproxy.cn https://goproxy.io 如果遇到某些包下载不下来的情况,可尝试更换数据源 更推荐使用https://goproxy.cn 速度快,缓存的包多 提醒…...

全网最适合入门的面向对象编程教程:31 Python的内置数据类型-对象Object和类型Type
全网最适合入门的面向对象编程教程:31 Python 的内置数据类型-对象 Object 和类型 Type 摘要: Python 中的对象和类型是一个非常重要的概念。在 Python 中,一切都是对象,包括数字、字符串、列表等,每个对象都有自己的类型。 原文链接: Fre…...
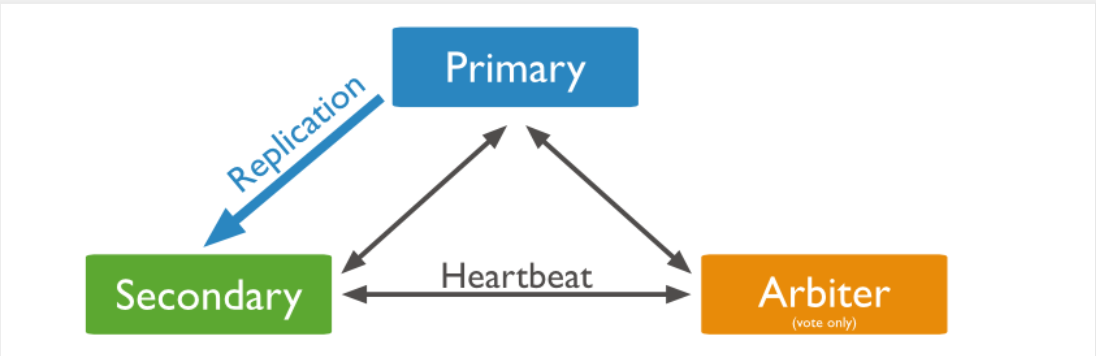
【mongodb】mongodb副本集的搭建和使用
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

Java后端面试复习7.24
lock加锁解锁尝试获取锁方法lock底层基于什么实现lock和lock的底层实现分别面向什么用户lock和synchronized异同如何选择合适的锁ReentrantLock如何实现冲入内部类三个公平和非公平获取锁怎么实现的RL默认公平还是非公平,构造参数ReentrantRedaWriteLock的特性什么是…...

前端 HTML 概述
目录 1. HTML概述 1.1 超文本标记语言 1.2 标签 2. HTML 解析与编辑 2.1 解析与访问 2.2 编辑 html文件 1. HTML概述 HTML( Hyper Text Markup Language:超文本标记语言 ):主要用于网页主体结构的搭建,在网页上…...
)
探索Thymeleaf:用动态Web模板引擎打造吸引人的用户界面(SpringBoot的html详解)
什么是Thymeleaf? Thymeleaf是一个用于Web和独立环境的现代服务器端Java模板引擎,用于处理XML/XHTML/HTML5内容。它特别适合基于Spring框架的Web应用程序,因为它提供了与Spring MVC的出色集成。Thymeleaf以其自然的模板语法和强大的数据绑定…...

视频教程 - 自研Vue3 Tree组件高级功能:虚拟滚动新增节点实现自动滚动
感谢小伙伴们对本套自研vue3 tree组件教程的关注,在前一篇媲美Element Plus JuanTree终极实战:虚拟滚动的功能演示中发现了小bug,特地整理了相关录屏来说明怎么一步步解决bug的,来回馈小伙伴们的支持。 Tree组件高级功能ÿ…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
