【C语言】Top K问题【建小堆】
前言
TopK问题:从n个数中,找出最大(或最小)的前k个数。
在我们生活中,经常会遇到TopK问题
比如外卖的必吃榜;成单的前K名;各种数据的最值筛选
问题分析

显然想开出40G的空间是不现实的,那应该怎么办呢?
答案是:建小堆

代码实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>// 造数据
void CreateNDate()
{// 造数据int n = 10000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}
void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}
//向下调整算法
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void PrintTopK(int k)
{FILE* fout = fopen("data.txt", "r");if (fout == NULL){perror("fopen mail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("minheap mail");return;}for (int i = 0; i < k; i++){fscanf_s(fout, "%d", &minheap[i]);}//建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(minheap, k, i);}int x = 0;int val = 0;while (val = fscanf_s(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}fclose(fout);
}
int main()
{//CreateNDate();printf("请输入k:>");int k = 0;scanf_s("%d", &k);PrintTopK(k);return 0;
}
运行结果:

结果验证
那我们怎么确定输出在屏幕上的数据就是最大的数据呢?
我们可以在已经创建的数据上面修改,如图后面111的是在原有数据上手动添加的

重新运行,结果与预期一致

相关文章:

【C语言】Top K问题【建小堆】
前言 TopK问题:从n个数中,找出最大(或最小)的前k个数。 在我们生活中,经常会遇到TopK问题 比如外卖的必吃榜;成单的前K名;各种数据的最值筛选 问题分析 显然想开出40G的空间是不现实的&#…...

Rust 程序设计语言学习——并发编程
安全且高效地处理并发编程是 Rust 的另一个主要目标。并发编程(Concurrent programming),代表程序的不同部分相互独立地执行,而并行编程(parallel programming)代表程序不同部分同时执行,这两个…...

联邦学习研究综述【联邦学习】
文章目录 0 前言机器学习两大挑战: 1 什么是联邦学习?联邦学习的一次迭代过程如下:联邦学习技术具有以下几个特点: 2 联邦学习的算法原理目标函数本地目标函数联邦学习的迭代过程 3 联邦学习分类横向联邦学习纵向联邦学习联邦迁移…...

深入理解Python中的列表推导式
深入理解Python中的列表推导式 在Python编程中,列表推导式(List Comprehension)是一种简洁而强大的语法,用于创建和操作列表。它不仅提高了代码的可读性,还能显著减少代码的行数。本文将详细介绍什么是列表推导式,如何使用它,以及一些实际应用示例,帮助读者更好地理解…...

Android 实现左侧导航栏:NavigationView是什么?NavigationView和Navigation搭配使用
目录 1)左侧导航栏效果图 2)NavigationView是什么? 3)NavigationView和Navigation搭配使用 4)NavigationView的其他方法 一、实现左侧导航栏 由于Android这边没有直接提供左侧导航栏的控件,所以我尝试了…...

如何快速下载拼多多图片信息,效率高
图片是电商吸引顾客的关键因素,高质量的商品图片能提升产品吸引力,增强用户购买欲望。良好的视觉展示有助于建立品牌形象,提高转化率。同时,图片也是商品信息的主要传递媒介,对消费者决策过程至关重要。 使用图快下载器…...

windows 10下,修改ubuntu的密码
(1)在搜索框里面输入cmd,然后点击右键,选择管理员打开 Microsoft Windows [版本 10.0.22631.3880] (c) Microsoft Corporation。保留所有权利。 C:\Windows\System32>C: C:\Windows\System32>cd ../../ C:\>cd Users\ASUS\AppData\Local\Micros…...

【MySQL】慢sql优化全流程解析
定位慢sql 工具排查慢sql 调试工具:Arthas运维工具:Skywalking 通过以上工具可以看到哪个接口比较慢,并且可以分析SQL具体的执行时间,定位到哪个sql出了问题。 启用慢查询日志 慢查询日志记录了所有执行时间超过指定参数(lon…...

RabbitMQ高级特性 - 消息分发(限流、负载均衡)
文章目录 RabbitMQ 消息分发概述如何实现消费分发机制(限制每个队列消息数量)使用场景限流背景实现 demo 非公平发送(负载均衡)背景实现 demo RabbitMQ 消息分发 概述 RabbitMQ 的队列在有多个消费者订阅时,默认会通过…...
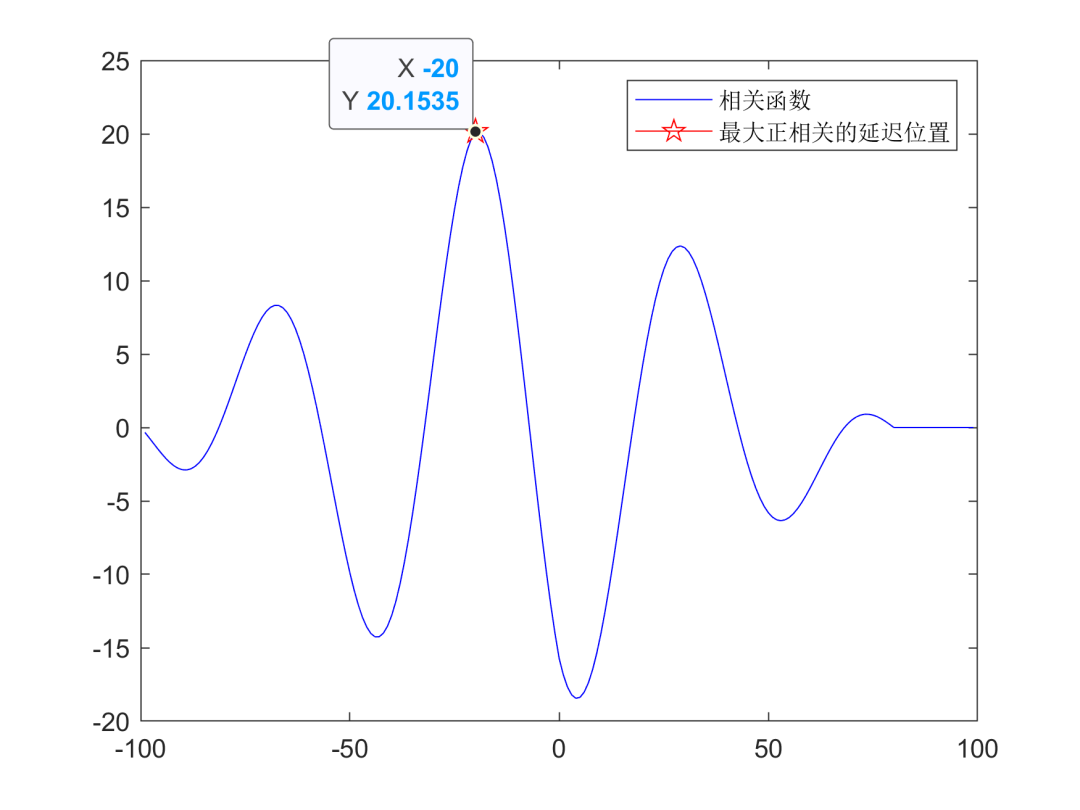
信号处理——自相关和互相关分析
1.概括 在信号处理中,自相关和互相关是相关分析非常重要的概念,它们能分析一个信号或两个信号在时间维度的相似性,在振动测试分析、雷达测距和声发射探伤得到了广泛的应用。自相关分析的研究对象为一个信号,互相关分析的研究对象…...
如何解决部分设备分辨率不适配
1)如何解决部分设备分辨率不适配 2)Unity中如何实现草的LOD 3)使用了Play Asset Delivery提交版本被Google报错 4)如何计算弧线弹道的落地位置 这是第396篇UWA技术知识分享的推送,精选了UWA社区的热门话题,…...

C#插件 调用存储过程(输出参数类型)
存储过程 CREATE PROCEDURE [dbo].[GetSum]num1 INT,num2 INT,result INT OUTPUT AS BEGINselect result num1 num2 END C#代码 using Kingdee.BOS; using Kingdee.BOS.App.Data; using Kingdee.BOS.Core.Bill.PlugIn; using Kingdee.BOS.Util; using System; using System.…...

代码随想录算法训练营day32 | 509. 斐波那契数 、70. 爬楼梯 、746. 使用最小花费爬楼梯
碎碎念:开始动态规划了!加油! 参考:代码随想录 动态规划理论基础 动态规划常见类型: 动规基础类题目背包问题打家劫舍股票问题子序列问题 解决动态规划问题应该要思考清楚的: 动态规划五部曲࿱…...

【人工智能专栏】Learning Rate Decay 学习率衰减
Learning Rate Decay 学习率衰减 使用格式 optimizer = torch.optim.SGD(model.paraters(), lr=0.1, momentum=0.9, weight_decay=1e-4) scheduler = torch.optim...
》题目集)
浙大版《C语言程序设计(第3版)》题目集
练习4-11 统计素数并求和 本题要求统计给定整数M和N区间内素数的个数并对它们求和。 输入格式: 输入在一行中给出两个正整数M和N(1≤M≤N≤500)。 输出格式: 在一行中顺序输出M和N区间内素数的个数以及它们的和,数字间以空格分隔。 输入…...

【学习笔记】Day 2
一、进度概述 1、inversionnet_train_light 试运行——未成功 2、DL-FWI基础入门培训-1,2,以及作业1的完成——暂未完成作业 二、详情 1、inversionnet_train_light 试运行 在补充完相关依赖后,运行仍有报错 产生原因:这个代码在当…...

Java中的Map(如果想知道Java中有关Map的知识点,那么只看这一篇就足够了!)
前言:在Java编程语言中,集合框架(Collection Framework)提供了一系列用于存储和操作数据的接口和类。其中,Map和Set是两个非常重要的接口,分别用于存储键值对和无重复元素的集合。 ✨✨✨这里是秋刀鱼不做梦…...

裸金属服务器详解
在云计算飞速发展的今天,裸金属服务器(Bare Metal Server, BMS)作为一种兼具传统物理服务器性能和虚拟化服务优势的计算资源,正逐渐成为企业和个人用户的重要选择。今天我们就来了解下关于裸金属服务器的定义、核心特点以及其在各…...

等待唤醒机制两种实现方法-阻塞队列
桌子上有面条-》吃货执行 桌子上没面条-》生产者制造执行 1、消费者等待 消费者先抢到CPU执行权,发现桌子上没有面条,于是变成等待wait状态,并释放CPU执行权,此时的CPU肯定会被厨师抢到,初始开始做面条,…...

数组项相加和 – 如何将 JavaScript 数组中的数字相加
JavaScript 中的数组是一个对象,它允许您在单个变量名称下存储多个值的有序集合,并以多种方式操作这些值。 在本文中,您将学习如何使用几种不同的方法计算给定数组中所有数字的总和。 具体来说,使用以下方法得到数组中所有数字的总…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
