【机器学习第7章——贝叶斯分类器】
机器学习第7章——贝叶斯分类器
- 7.贝叶斯分类器
- 7.1贝叶斯决策论
- 7.2 朴素贝叶斯分类器
- 条件概率的m估计
- 7.3 极大似然估计
- 优点
- 基本原理
- 7.4 贝叶斯网络
- 7.5 半朴素贝叶斯分类器
- 7.6 EM算法
- 7.7 EM算法实现
7.贝叶斯分类器
7.1贝叶斯决策论
-
一个医疗判断问题
-
有两个可选的假设:病人有癌症;病人无癌症
-
可用数据来自化验结果:正+和负-
-
有先验知识
- 在所有人口中,患病率是0.008
- 对确实有病的患者的化验准确率是0.98
- 对确实无病的患者的化验准确率是0.97、
-
总结如下
P ( c a n c e r ) = 0.008 , p ( ¬ c a n c e r ) 0.992 P ( + ∣ c a n c e r ) = 0.98 , p ( − ∣ c a n c e r ) 0.02 P ( + ∣ ¬ c a n c e r ) = 0.08 , p ( − ∣ c a n c e r ) 0.97 P(cancer)=0.008,p(\neg cancer)0.992\\ P(+|cancer)=0.98,p(-|cancer)0.02\\ P(+|\neg cancer)=0.08,p(-|cancer)0.97\\ P(cancer)=0.008,p(¬cancer)0.992P(+∣cancer)=0.98,p(−∣cancer)0.02P(+∣¬cancer)=0.08,p(−∣cancer)0.97 -
问题:假定有一个新病人,化验结果为正,是否应将病人断定为有癌症?求后验概率
P ( c a n c e r ∣ + ) , p ( ¬ c a n c e r ∣ + ) P(cancer|+),p(\neg cancer|+)\\ P(cancer∣+),p(¬cancer∣+)
-
-
贝叶斯定理的意义在于,我们在生活中经常遇到这种情况:
- 我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A)。
-
贝叶斯定理
P ( B ∣ A ) = P ( A ∣ B ) P ( B ) P ( A ) P(B|A)=\frac{P(A|B)P(B)}{P(A)} P(B∣A)=P(A)P(A∣B)P(B) -
例子:有一家企业M提供产品和服务,企业K考虑是否进入该市场。同时企业M会阻止K进入该市场,而企业K能否进入该市场完全取决于M为组织其进入所花费的成本大小。
- 假设K并不知道M是属于高阻挠成本类型还是低阻挠成本类型
- 如果M属于高阻挠成本类型,K进入市场时,M进行阻挠的概率是20%
- 如果M属于低阻挠成本类型,K进入市场时,M进行阻挠的概率是100%
- 现设K认为M属于高阻挠成本企业的概率为70%,K进入市场后,M进行了阻挠,判断企业M为高阻挠成本类型的概率。
- 假设K并不知道M是属于高阻挠成本类型还是低阻挠成本类型

- 综上,M为高阻挠成本类型的概率为0.32,也就是说M为低阻挠成本类型的概率为0.68,即M更有可能是低阻挠成本类型
7.2 朴素贝叶斯分类器
给定类标号y,朴素贝叶斯分类器在估计类条件概率时假设属性之间条件独立。条件独立假设可以形式化的表达如下:
P ( X ∣ Y = y ) = ∏ i = 1 n P ( x i ∣ Y = y ) 其中每个训练样本可用一个属性向量 X = ( x 1 , x 2 , x 3 , . . . , x n ) 表示,各个属性之间条件独立 P(X|Y=y)=\prod_{i=1}^n P(x_i|Y=y)\\ 其中每个训练样本可用一个属性向量X=(x_1,x_2,x_3,...,x_n)表示,各个属性之间条件独立 P(X∣Y=y)=i=1∏nP(xi∣Y=y)其中每个训练样本可用一个属性向量X=(x1,x2,x3,...,xn)表示,各个属性之间条件独立
- 假设给定的训练样本数据,计算
x = ( o u t l o o k = S u n n y t e m p e r a t u r e = C o o l h u m d i t y = H i g h w i n d = S t r o n g ) , y = [ y e s , n o ] x=\begin{pmatrix} outlook=Sunny \\ temperature=Cool \\ humdity=High \\ wind =Strong \end{pmatrix},y=[yes,no] x= outlook=Sunnytemperature=Coolhumdity=Highwind=Strong ,y=[yes,no]
| Day | Outlook | Temperate | Humidity | Wind | Play Tennis |
|---|---|---|---|---|---|
| D1 | Sunny | Hot | High | Weak | No |
| D2 | Sunny | Hot | High | Strong | No |
| D3 | Overcast | Hot | High | Weak | Yes |
| D4 | Rain | Mild | High | Weak | Yes |
| D5 | Rain | Cool | Normal | Weak | Yes |
| D6 | Rain | Cool | Normal | Strong | No |
| D7 | Overcast | Cool | Normal | Strong | Yes |
| D8 | Sunny | Mild | High | Weak | No |
| D9 | Sunny | Cool | Normal | Weak | Yes |
| D10 | Rain | Mild | Normal | Weak | Yes |
| D11 | Sunny | Mild | Normal | Strong | Yes |
| D12 | Overcast | Mild | High | Strong | Yes |
| D13 | Overcast | Hot | Normal | Weak | Yes |
| D14 | Rain | Mild | High | Strong | No |

-
对于如果存在连续属性来说,假定概率服从高斯分布,则
μ c , i 和 σ c , i 2 表示第 c 类样本在第 i 个属性上取值的均值和方差 \mu_{c,i}和\sigma_{c,i}^2表示第c类样本在第i个属性上取值的均值和方差\\ μc,i和σc,i2表示第c类样本在第i个属性上取值的均值和方差p ( x i ∣ c ) = 1 2 π σ c , i e − ( x i − μ c , i ) 2 2 σ c , i 2 p(x_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}e^{-\frac{(x_i-\mu_{c,i})^2}{2\sigma_{c,i}^2}} p(xi∣c)=2πσc,i1e−2σc,i2(xi−μc,i)2
- 假如有一个西瓜的密度为0.697,样本中好瓜密度的均值为0.574,好瓜标准差为0.129
p ( 密度 = 0.697 ∣ 好瓜 = 是 ) = 1 2 π × 0.129 e − ( 0.697 − 0.574 ) 2 2 × 0.12 9 2 ≈ 1.959 p(密度=0.697|好瓜=是)=\frac{1}{\sqrt{2\pi}\times0.129}e^{-\frac{(0.697-0.574)^2}{2\times0.129^2}}\approx1.959 p(密度=0.697∣好瓜=是)=2π×0.1291e−2×0.1292(0.697−0.574)2≈1.959
剩下的属性计算步骤与上例相同
- 假如有一个西瓜的密度为0.697,样本中好瓜密度的均值为0.574,好瓜标准差为0.129
-
但是这样存在一个问题,假设来了一个新样本
x = ( o u t l o o k = C l o u d y t e m p e r a t u r e = C o o l h u m d i t y = H i g h w i n d = S t r o n g ) x=\begin{pmatrix} outlook=Cloudy \\ temperature=Cool \\ humdity=High \\ wind =Strong \end{pmatrix} x= outlook=Cloudytemperature=Coolhumdity=Highwind=Strong
进行计算会发现
P ( o u t l o o k = C l o u d y ∣ Y = y e s ) = 0 9 = 0 P ( o u t l o o k = C l o u d y ∣ Y = n o ) = 0 5 = 0 P(outlook=Cloudy|Y=yes)=\frac{0}{9}=0\\ P(outlook=Cloudy|Y=no)=\frac{0}{5}=0 P(outlook=Cloudy∣Y=yes)=90=0P(outlook=Cloudy∣Y=no)=50=0
这样到最后会使整个式子等于0,没有记录到并不等于出现的概率是0,所以提出了条件概率的m估计
条件概率的m估计
当训练样本不能覆盖那么多的属性值时,都会出现上述的窘境。简单的使用样本比例来估计类条件概率的方法太脆弱了,尤其是当训练样本少而属性数目又很大时。解决方法是使用m估计方法来估计条件概率
P ( X i ∣ Y ) = n c + m p n + m P(X_i|Y)=\frac{n_c+mp}{n+m} P(Xi∣Y)=n+mnc+mp
n 是 Y 中的样本总数 n c 是 Y 中取值 x i 的样本数 m 是称为等价样本大小的参数 p 是用户指定的参数 n是Y中的样本总数\\ n_c是Y中取值x_i的样本数\\ m是称为等价样本大小的参数\\ p是用户指定的参数 n是Y中的样本总数nc是Y中取值xi的样本数m是称为等价样本大小的参数p是用户指定的参数
也就是说,在分子和分母上同时加上一点儿数,使得分数不要为0
-
多项式模型
-
基本原理:在多项式模型,设某文档
d = ( t 1 , t 2 , . . . , t k ) t k 是出现过的单词,允许重复 d=(t_1,t_2,...,t_k)\\ t_k是出现过的单词,允许重复 d=(t1,t2,...,tk)tk是出现过的单词,允许重复 -
先验概率
p ( c ) = 类 c 下单词总数 整个训练本的单词总数 p(c)=\frac{类c下单词总数}{整个训练本的单词总数} p(c)=整个训练本的单词总数类c下单词总数 -
条件概率
P ( t k ∣ c ) = 类 c 下单词 t k 在各个文档中出现的次数 + 1 类 c 下单词总数 + ∣ v ∣ v 是训练样本的单词表(即抽取单词,单词出现多次,只算一个) 此时 m = ∣ v ∣ , p = 1 ∣ v ∣ P(t_k|c)=\frac{类c下单词t_k在各个文档中出现的次数+1}{类c下单词总数+|v|}\\ v是训练样本的单词表(即抽取单词,单词出现多次,只算一个)\\ 此时m=|v|,p=\frac{1}{|v|} P(tk∣c)=类c下单词总数+∣v∣类c下单词tk在各个文档中出现的次数+1v是训练样本的单词表(即抽取单词,单词出现多次,只算一个)此时m=∣v∣,p=∣v∣1 -
给定一个新样本
d o c : C h i n e s e C h i n e s e C h i n e s e T o k y o J a p a n doc:Chinese\,\,\,Chinese\,\,\,Chinese\,\,\,Tokyo\,\,\,Japan doc:ChineseChineseChineseTokyoJapan
用属性向量表示为
d = ( C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) d=(Chinese,Chinese,Chinese,Tokyo,Japan) d=(Chinese,Chinese,Chinese,Tokyo,Japan)
-
| id | doc | 类别 in China? |
|---|---|---|
| 1 | Chinese Beijing Chinese | yes |
| 2 | Chinese Chinese Shanghai | yes |
| 3 | Chinese Macao | yes |
| 4 | Tokyo Japan Chinese | no |


-
伯努利模型
-
先验概率
p ( c ) = 类 c 下文件数 整个训练本的文件总数 p(c)=\frac{类c下文件数}{整个训练本的文件总数} p(c)=整个训练本的文件总数类c下文件数 -
条件概率
P ( t k ∣ c ) = 类 c 下单词 t k 的文件数 + 1 类 c 下文件数 + 2 此时 m = 2 , p = 1 2 P(t_k|c)=\frac{类c下单词t_k的文件数+1}{类c下文件数+2}\\ 此时m=2,p=\frac{1}{2} P(tk∣c)=类c下文件数+2类c下单词tk的文件数+1此时m=2,p=21p ( t c ∣ c = y e s ) = ∏ p ( t c ∣ c = y e s ) ( 1 − p ( t i ∣ c = y e s ) ) p(t_c|c=yes)=\prod p(t_c|c=yes)(1-p(t_i|c=yes)) p(tc∣c=yes)=∏p(tc∣c=yes)(1−p(ti∣c=yes))
-
给定一个新样本
d o c : C h i n e s e C h i n e s e C h i n e s e T o k y o J a p a n doc:Chinese\,\,\,Chinese\,\,\,Chinese\,\,\,Tokyo\,\,\,Japan doc:ChineseChineseChineseTokyoJapan
用属性向量表示为
d = ( C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) d=(Chinese,Chinese,Chinese,Tokyo,Japan) d=(Chinese,Chinese,Chinese,Tokyo,Japan)
-
| id | doc | 类别 in China? |
|---|---|---|
| 1 | Chinese Beijing Chinese | yes |
| 2 | Chinese Chinese Shanghai | yes |
| 3 | Chinese Macao | yes |
| 4 | Tokyo Japan Chinese | no |


- 模型比较
- 二者计算粒度不同,多项式以单词为粒度,而伯努利以文件为粒度
- 在后验概率计算中,多项式只会计算文档d出现过的单词的概率,而伯努利则会把所有单词的概率都算进去(有出现在文档d中的概率为p,没出现的为1-p)
- 运用贝叶斯定理所需概率
- P(B)(先验)
- P(A|B)(类条件密度)
- 但是大部分情况我们并不能获得到如此完善的信息
- 如果可以将类条件密度参数化,则可以显著降低难度
- 例如:P(A|B)的正态性,就将概率密度估计问题转化为参数估计问题
- 所以常见的估计有两种
- 极大似然估计(MLE)
- 将参数看作是确定的量,只是其值是未知,通过极大化所观察的样本概率得到最优的参数,接着通过分析得到参数的值
- 贝叶斯估计
- 把参数当成服从某种先验概率分布的随机变量,对样本进行观测的过程,就是把先验概率密度转化成为后验概率密度,使得对于每个新样本,后验概率密度函数在待估参数的真实值附近形成最大尖峰。
- 极大似然估计(MLE)
7.3 极大似然估计
优点
- 当样本数目增加时,收敛性质会更好
- 比其他可选择的技术更加简单
基本原理
D c D_c Dc
表示训练集D中第c类样本组合的集合,样本之间是独立同分布的,则参数
θ c \theta_c θc
对于数据集的似然是
P ( D c ∣ θ c ) = ∏ x ∈ D c P ( x ∣ θ c ) P(D_c|\theta_c)=\prod_{x\in D_c}P(x|\theta_c) P(Dc∣θc)=x∈Dc∏P(x∣θc)
但这样会造成数据的下溢,需要对其取对数
L L ( θ c ) = log P ( D c ∣ θ c ) LL(\theta_c)=\log P(D_c|\theta_c) LL(θc)=logP(Dc∣θc)
此时我们对对数似然函数的
θ c \theta_c θc
求导,并令导数为0,可求解出
θ ^ c \hat \theta_c θ^c
即为使对数似然最大的值,记为
θ ^ c = a r g max θ c L L ( θ c ) \hat \theta_c=arg\,\max_{\theta_c} LL(\theta_c) θ^c=argθcmaxLL(θc)
- 以高斯情况为例,x为标量的似然函数计算如下

- 机器学习中特征向量是多维的,这时候密度函数需要发生变化
X = [ x 1 , x 2 , . . , x n ] T , μ = [ μ 1 , μ 2 , . . . , μ n ] T 多维情况下将方差替换成协方差矩阵 ( ∑ ) X=[x_1,x_2,..,x_n]^T,\mu=[\mu_1,\mu_2,...,\mu_n]^T\\ 多维情况下将方差替换成协方差矩阵(\sum) X=[x1,x2,..,xn]T,μ=[μ1,μ2,...,μn]T多维情况下将方差替换成协方差矩阵(∑)
f ( X ) = 1 ( 2 π ) n ∣ ∑ ∣ 1 2 e − ( X − μ ) T ( X − μ ) 2 ∑ f(X)=\frac{1}{(\sqrt{2\pi})^n|\sum|^\frac{1}{2}}e^{-\frac{(X-\mu)^T(X-\mu)}{2\sum}} f(X)=(2π)n∣∑∣211e−2∑(X−μ)T(X−μ)
ln f ( X ) = − 1 2 ln [ ( 2 π ) n ∣ ∑ ∣ ] − 1 2 ( X − μ ) T ∑ − 1 ( X − μ ) ∑ − 1 : 协方差矩阵的逆 \ln f(X)=-\frac{1}{2}\ln[(2\pi)^n|\sum|]-\frac{1}{2}{(X-\mu)^T\sum^{-1}(X-\mu)}\\ \sum^{-1}:协方差矩阵的逆 lnf(X)=−21ln[(2π)n∣∑∣]−21(X−μ)T∑−1(X−μ)∑−1:协方差矩阵的逆

7.4 贝叶斯网络
-
贝叶斯网络是一个有向无环图,包含两个部分
- 节点:表示随机变量
- 节点间的有向边:表示节点间的互相关系
-
贝叶斯网络B(D,P),D表示一个有向无环图,P表示条件概率分布的集合
- 联合概率分布定义
P ( X ) = ∏ i = 1 n P ( X i ∣ π i ) X i = ( X 1 , X 2 , . . . , X n ) π i : X i 的父节点 P(X)=\prod_{i=1}^nP(X_i|\pi_i)\\ X_i=(X_1,X_2,...,X_n)\\ \pi_i:X_i的父节点 P(X)=i=1∏nP(Xi∣πi)Xi=(X1,X2,...,Xn)πi:Xi的父节点
- 联合概率分布定义

7.5 半朴素贝叶斯分类器
朴素贝叶斯分类器采用的是属性条件独立性假设,但是在现实任务中这个假设往往很难成立,所以就产生了半朴素贝叶斯分类器
基本思想:适当考虑一部分属性间的相互依赖信息,从而既不需要进行完全联合概率计算,又不至于彻底忽略比较强的属性依赖关系,“独依赖估计”(ODE)是最常用的一种策略,即每个属性在类别之外最多依赖于一个其他属性。以下又提供了两种半朴素贝叶斯分类器所考虑的属性依赖关系。

例如,样本集合如下

我们规定:脐部的依赖属性为敲声,且属性取值为凹陷时,依赖敲声为浊响
并且需要对概率进行修正

7.6 EM算法
-
极大似然估计存在着问题是:
- 对于许多具体问题不能构造似然函数解析表达式
- 似然函数的表达式过于复杂而导致求解方程组非常困难
-
所以提出了EM算法。EM算法主要用于非完全数据参数估计,它是通过假设隐变量的存在,极大化地简化了似然函数方程,从而解决了方程求解问题。
-
观测数据:观测到的随机变量y的独立同分布(IID)样本
Y = ( Y 1 , Y 2 , … , Y n ) Y=(Y_1,Y_2,…,Y_n) Y=(Y1,Y2,…,Yn) -
缺失数据:未观测到的随机变量Z的值
Z = ( Z 1 , Z 2 . … , Z n ) Z=(Z_1,Z_2.…,Z_n) Z=(Z1,Z2.…,Zn) -
完整数据:包含观测到的随机变量Y和未观测到的随机变量Z的数据,Z=(X,Y)
Z = ( ( X 1 , Y 1 ) , . . , ( X n , Y n ) ) Z=((X_1,Y_1),..,(X_n,Y_n)) Z=((X1,Y1),..,(Xn,Yn)) -
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。
-
EM算法的每次迭代由两步组成
- E步,求期望
- M步,求极大
-
三硬币模型
-
假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率概率分别是a,b,c。进行如下掷硬币试验:先掷A,根据其结果选出硬币B或C,正面选择硬币B,反面选硬币C;然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里n=10),观测结果如下:
1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 1,1,0,1,0,0,1,0,1,1 1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果,不能观测到掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数。 -
模型可写作

随机变量 y 是观测变量,表示一次试验观测的结果是 1 或 0 随机变量 z 是隐变量,表示未观测到的掷硬币 A 的结果 θ = ( a , b , c ) 是模型参数 随机变量y是观测变量,表示一次试验观测的结果是1或0\\ 随机变量z是隐变量,表示未观测到的掷硬币A的结果\\ \theta=(a,b,c)是模型参数 随机变量y是观测变量,表示一次试验观测的结果是1或0随机变量z是隐变量,表示未观测到的掷硬币A的结果θ=(a,b,c)是模型参数
-
将观测数据表示为
Y = ( y 1 , y 2 , . . . , y n ) T Y=(y_1,y_2,...,y_n)^T Y=(y1,y2,...,yn)T
未观测数据表示为
Z = ( z 1 , z 2 , . . . , z n ) T Z=(z_1,z_2,...,z_n)^T Z=(z1,z2,...,zn)T
则观测数据的似然函数为
P ( Y ∣ θ ) = ∑ Z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) P(Y|\theta)=\sum_ZP(Z|\theta)P(Y|Z,\theta) P(Y∣θ)=Z∑P(Z∣θ)P(Y∣Z,θ)
即
P ( Y ∣ θ ) = ∏ j = 1 n [ a b y j ( 1 − b ) 1 − y j + ( 1 − a ) c y j ( 1 − c ) 1 − y j ] P(Y|\theta)=\prod_{j=1}^n[ab^{y_j}(1-b)^{1-y_j}+(1-a)c^{y_j}(1-c)^{1-y_j}] P(Y∣θ)=j=1∏n[abyj(1−b)1−yj+(1−a)cyj(1−c)1−yj]
考虑求模型参数的极大似然估计
θ ^ = a r g max θ log P ( Y ∣ θ ) \hat\theta=arg\,\,\max_\theta\,\log P(Y|\theta) θ^=argθmaxlogP(Y∣θ)
只能通过迭代的方式进行求解 -
EM算法首先选取参数的初值
θ ( 0 ) = ( a ( 0 ) , b ( 0 ) , c ( 0 ) ) \theta^{(0)}=(a^{(0)},b^{(0)},c^{(0)}) θ(0)=(a(0),b(0),c(0))
然后通过以下步骤迭代计算参数的估计值,直至收敛为止。第i次迭代参数的估计值为
θ ( i ) = ( a ( i ) , b ( i ) , c ( i ) ) \theta^{(i)}=(a^{(i)},b^{(i)},c^{(i)}) θ(i)=(a(i),b(i),c(i))
第i+1次迭代如下-
E步:计算在模型参数
a ( i ) , b ( i ) , c ( i ) a^{(i)},b^{(i)},c^{(i)} a(i),b(i),c(i)上标为迭代次数 \color{red}{上标为迭代次数} 上标为迭代次数
下观测数据
y j y_j yj下标为样本编号 \color{red}{下标为样本编号} 下标为样本编号
来自掷到硬币B的概率
P ( z j = B ∣ y j , θ ) = a ( i ) ( b ( i ) ) y j ( 1 − b ( i ) ) 1 − y j a ( i ) ( b ( i ) ) y j ( 1 − b ( i ) ) 1 − y j + ( 1 − a ( i ) ) ( c ( i ) ) y j ( 1 − c ( i ) ) 1 − y j ( 1 ) P(z_j=B|y_j,\theta)=\frac{a^{(i)}(b^{(i)})^{y_j}(1-b^{(i)})^{1-y_j}}{a^{(i)}(b^{(i)})^{y_j}(1-b^{(i)})^{1-y_j}+(1-a^{(i)})(c^{(i)})^{y_j}(1-c^{(i)})^{1-y_j}}\quad(1) P(zj=B∣yj,θ)=a(i)(b(i))yj(1−b(i))1−yj+(1−a(i))(c(i))yj(1−c(i))1−yja(i)(b(i))yj(1−b(i))1−yj(1)
并把
P ( z j = B ∣ y j , θ ) 记作 μ ( j ) 1 − μ ( j ) 即表示为掷到硬币 C 的概率 P(z_j=B|y_j,\theta)记作\mu^{(j)}\\ 1-\mu^{(j)}即表示为掷到硬币C的概率 P(zj=B∣yj,θ)记作μ(j)1−μ(j)即表示为掷到硬币C的概率
计算似然函数的期望
Q ( θ ) = P ( Z ∣ Y , θ ) log P ( Y , Z ∣ θ ) = ∑ i = 1 n [ μ i log a b y i ( 1 − b ) 1 − y i + ( 1 − μ i ) log ( 1 − a ) c y i ( 1 − c ) 1 − y i ] = ∑ i = 1 n { μ i ( log a + y i log b + ( 1 − y i ) log ( 1 − b ) ) + ( 1 − μ i ) ( log ( 1 − a ) + y i log c + ( 1 − y i ) log ( 1 − c ) ) } ( 2 ) Q(\theta)=P(Z|Y,\theta)\log P(Y,Z|\theta) \\=\sum_{i=1}^n[\mu_i\log ab^{y_i}(1-b)^{1-y_i}+(1-\mu_i)\log(1-a)c^{y_i}(1-c)^{1-y_i}]\\ =\sum_{i=1}^n\{\mu_i(\log a +y_i\log b+(1-y_i)\log(1-b))+\\(1-\mu_i)(\log(1-a) +y_i\log c+(1-y_i)\log(1-c))\}\quad(2) Q(θ)=P(Z∣Y,θ)logP(Y,Z∣θ)=i=1∑n[μilogabyi(1−b)1−yi+(1−μi)log(1−a)cyi(1−c)1−yi]=i=1∑n{μi(loga+yilogb+(1−yi)log(1−b))+(1−μi)(log(1−a)+yilogc+(1−yi)log(1−c))}(2) -
M步:求似然函数的极大值
-
对a求偏导
∂ Q ∂ a = ∑ i = 1 n ( μ i a − 1 − μ i 1 − a ) = 1 a ( 1 − a ) ∑ i = 1 n ( μ i − a ) = 0 1 a ( 1 − a ) ( ∑ i = 1 n μ i − n a ) = 0 a = 1 n ∑ i = 1 n μ i \frac{\partial Q}{\partial a}=\sum_{i=1}^n(\frac{\mu_i}{a}-\frac{1-\mu_i}{1-a})=\frac{1}{a(1-a)}\sum_{i=1}^n(\mu_i-a)=0\\ \frac{1}{a(1-a)}(\sum_{i=1}^n\mu_i-na)=0\\ a=\frac{1}{n}\sum_{i=1}^n\mu_i ∂a∂Q=i=1∑n(aμi−1−a1−μi)=a(1−a)1i=1∑n(μi−a)=0a(1−a)1(i=1∑nμi−na)=0a=n1i=1∑nμi -
对b求偏导
∂ Q ∂ b = ∑ i = 1 n μ i ( y i b − 1 − y i 1 − b ) = 1 b ( 1 − b ) ∑ i = 1 n μ i ( y i − b ) = 0 ∑ i = 1 n μ i y i − b ∑ i = 1 n μ i = 0 b = ∑ i = 1 n μ i y i ∑ i = 1 n μ i \frac{\partial Q}{\partial b}=\sum_{i=1}^n\mu_i(\frac{y_i}{b}-\frac{1-y_i}{1-b})=\frac{1}{b(1-b)}\sum_{i=1}^n\mu_i(y_i-b)=0\\ \sum_{i=1}^n\mu_iy_i-b\sum_{i=1}^n\mu_i=0\\ b=\frac{\sum_{i=1}^n\mu_iy_i}{\sum_{i=1}^n\mu_i} ∂b∂Q=i=1∑nμi(byi−1−b1−yi)=b(1−b)1i=1∑nμi(yi−b)=0i=1∑nμiyi−bi=1∑nμi=0b=∑i=1nμi∑i=1nμiyi -
对c求偏导
∂ Q ∂ c = ∑ i = 1 n ( 1 − μ i ) ( y i c − 1 − y i 1 − c ) = 1 c ( 1 − c ) ∑ i = 1 n ( 1 − μ i ) ( y i − c ) = 0 ∑ i = 1 n ( 1 − μ i ) y i − c ∑ i = 1 n ( 1 − μ i ) = 0 c = ∑ i = 1 n ( 1 − μ i ) y i ∑ i = 1 n ( 1 − μ i ) \frac{\partial Q}{\partial c}=\sum_{i=1}^n(1-\mu_i)(\frac{y_i}{c}-\frac{1-y_i}{1-c})=\frac{1}{c(1-c)}\sum_{i=1}^n(1-\mu_i)(y_i-c)=0\\ \sum_{i=1}^n(1-\mu_i)y_i-c\sum_{i=1}^n(1-\mu_i)=0\\ c=\frac{\sum_{i=1}^n(1-\mu_i)y_i}{\sum_{i=1}^n(1-\mu_i)} ∂c∂Q=i=1∑n(1−μi)(cyi−1−c1−yi)=c(1−c)1i=1∑n(1−μi)(yi−c)=0i=1∑n(1−μi)yi−ci=1∑n(1−μi)=0c=∑i=1n(1−μi)∑i=1n(1−μi)yi
-
-
计算完成后,可以计算模型参数的新估计值
a ( j + 1 ) = 1 n ∑ i = 1 n μ i ( j + 1 ) ( 3 ) a^{(j+1)}=\frac{1}{n}\sum_{i=1}^n\mu_i^{(j+1)}\quad (3) a(j+1)=n1i=1∑nμi(j+1)(3)b ( j + 1 ) = ∑ i = 1 n μ i ( j + 1 ) y i ∑ i = 1 n μ i ( j + 1 ) ( 4 ) b^{(j+1)}=\frac{\sum_{i=1}^n\mu_i^{(j+1)}y_i}{\sum_{i=1}^n\mu_i^{(j+1)}}\quad (4) b(j+1)=∑i=1nμi(j+1)∑i=1nμi(j+1)yi(4)
c ( j + 1 ) = ∑ i = 1 n ( 1 − μ i ( j + 1 ) ) y i ∑ i = 1 n ( 1 − μ i ( j + 1 ) ) ( 5 ) c^{(j+1)}=\frac{\sum_{i=1}^n(1-\mu_i^{(j+1)})y_i}{\sum_{i=1}^n(1-\mu_i^{(j+1)})}\quad (5) c(j+1)=∑i=1n(1−μi(j+1))∑i=1n(1−μi(j+1))yi(5)
-
然后进行计算,假设模型参数的初始值为
a ( 0 ) = 0.5 , b ( 0 ) = 0.5 , c ( 0 ) = 0.5 a^{(0)}=0.5,b^{(0)}=0.5,c^{(0)}=0.5 a(0)=0.5,b(0)=0.5,c(0)=0.5
由式(1),对十次试验进行计算
回顾十次试验结果 : 1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 回顾十次试验结果:1,1,0,1,0,0,1,0,1,1 回顾十次试验结果:1,1,0,1,0,0,1,0,1,1μ 1 ( 1 ) = 0.5 × 0. 5 1 × ( 1 − 0.5 ) 1 − 1 0.5 × 0. 5 1 × ( 1 − 0.5 ) 1 − 1 + ( 1 − 0.5 ) × 0. 5 1 × ( 1 − 0.5 ) 1 − 1 = 0.5 \mu_1^{(1)}=\frac{0.5\times 0.5^1\times (1-0.5)^{1-1}}{0.5\times 0.5^1\times (1-0.5)^{1-1}+(1-0.5)\times 0.5^1\times (1-0.5)^{1-1}}=0.5 μ1(1)=0.5×0.51×(1−0.5)1−1+(1−0.5)×0.51×(1−0.5)1−10.5×0.51×(1−0.5)1−1=0.5
μ 3 ( 1 ) = 0.5 × 0. 5 0 × ( 1 − 0.5 ) 1 − 0 0.5 × 0. 5 0 × ( 1 − 0.5 ) 1 − 0 + ( 1 − 0.5 ) × 0. 5 0 × ( 1 − 0.5 ) 1 − 0 = 0.5 \mu_3^{(1)}=\frac{0.5\times 0.5^0\times (1-0.5)^{1-0}}{0.5\times 0.5^0\times (1-0.5)^{1-0}+(1-0.5)\times 0.5^0\times (1-0.5)^{1-0}}=0.5 μ3(1)=0.5×0.50×(1−0.5)1−0+(1−0.5)×0.50×(1−0.5)1−00.5×0.50×(1−0.5)1−0=0.5
经过计算可知:
μ j ( 1 ) = 0.5 , j = 1 , 2 , . . . , 10 \mu_j^{(1)}=0.5,\quad j=1,2,...,10 μj(1)=0.5,j=1,2,...,10- 利用(3)(4)(5)式进行第一次迭代
a ( 1 ) = 1 10 ∑ i = 1 10 μ i ( 1 ) = 0.5 a^{(1)}=\frac{1}{10}\sum_{i=1}^{10}\mu_i^{(1)}=0.5 a(1)=101i=1∑10μi(1)=0.5
b ( 1 ) = ∑ i = 1 10 μ i ( 1 ) y i ∑ i = 1 10 μ i ( 1 ) = 0.5 × ( 1 + 1 + 0 + 1 + 0 + 0 + 1 + 0 + 1 + 1 ) 0.5 × 10 = 0.6 b^{(1)}=\frac{\sum_{i=1}^{10}\mu_i^{(1)}y_i}{\sum_{i=1}^{10}\mu_i^{(1)}}\\ =\frac{0.5\times(1+1+0+1+0+0+1+0+1+1)}{0.5\times 10}\\ =0.6 b(1)=∑i=110μi(1)∑i=110μi(1)yi=0.5×100.5×(1+1+0+1+0+0+1+0+1+1)=0.6
c ( 1 ) = ∑ i = 1 10 ( 1 − μ i ( 1 ) ) y i ∑ i = 1 10 ( 1 − μ i ( 1 ) ) = ( 1 − 0.5 ) × ( 1 + 1 + 0 + 1 + 0 + 0 + 1 + 0 + 1 + 1 ) ( 1 − 0.5 ) × 10 = 0.6 c^{(1)}=\frac{\sum_{i=1}^{10}(1-\mu_i^{(1)})y_i}{\sum_{i=1}^{10}(1-\mu_i^{(1)})}\\ =\frac{(1-0.5)\times(1+1+0+1+0+0+1+0+1+1)}{(1-0.5)\times 10}\\ =0.6 c(1)=∑i=110(1−μi(1))∑i=110(1−μi(1))yi=(1−0.5)×10(1−0.5)×(1+1+0+1+0+0+1+0+1+1)=0.6
经过一轮计算后,再由式(1)计算,可得:
μ 1 ( 2 ) = 0.5 × ( 0.6 ) 1 × ( 1 − 0.6 ) 1 − 1 0.5 × ( 0.6 ) 1 × ( 1 − 0.6 ) 1 − 1 + ( 1 − 0.5 ) × ( 0.6 ) 1 × ( 1 − 0.6 ) 1 − 1 = 0.5 \mu_1^{(2)}=\frac{0.5\times(0.6)^1\times(1-0.6)^{1-1}}{0.5\times(0.6)^1\times(1-0.6)^{1-1}+(1-0.5)\times(0.6)^1\times(1-0.6)^{1-1}}\\ =0.5 μ1(2)=0.5×(0.6)1×(1−0.6)1−1+(1−0.5)×(0.6)1×(1−0.6)1−10.5×(0.6)1×(1−0.6)1−1=0.5μ 3 ( 2 ) = 0.5 × ( 0.6 ) 0 × ( 1 − 0.6 ) 1 − 0 0.5 × ( 0.6 ) 0 × ( 1 − 0.6 ) 1 − 0 + ( 1 − 0.5 ) × ( 0.6 ) 0 × ( 1 − 0.6 ) 1 − 0 = 0.5 \mu_3^{(2)}=\frac{0.5\times(0.6)^0\times(1-0.6)^{1-0}}{0.5\times(0.6)^0\times(1-0.6)^{1-0}+(1-0.5)\times(0.6)^0\times(1-0.6)^{1-0}}\\ =0.5 μ3(2)=0.5×(0.6)0×(1−0.6)1−0+(1−0.5)×(0.6)0×(1−0.6)1−00.5×(0.6)0×(1−0.6)1−0=0.5
经过计算可知:
μ j ( 2 ) = 0.5 , j = 1 , 2 , . . . , 10 \mu_j^{(2)}=0.5,\quad j=1,2,...,10 μj(2)=0.5,j=1,2,...,10- 进行第二次迭代
a ( 2 ) = 1 10 ∑ i = 1 10 μ i ( 2 ) = 0.5 a^{(2)}=\frac{1}{10}\sum_{i=1}^{10}\mu_i^{(2)}=0.5 a(2)=101i=1∑10μi(2)=0.5
b ( 2 ) = ∑ i = 1 10 μ i ( 2 ) y i ∑ i = 1 10 μ i ( 2 ) = 0.6 b^{(2)}=\frac{\sum_{i=1}^{10}\mu_i^{(2)}y_i}{\sum_{i=1}^{10}\mu_i^{(2)}}\\ =0.6 b(2)=∑i=110μi(2)∑i=110μi(2)yi=0.6
c ( 2 ) = ∑ i = 1 10 ( 1 − μ i ( 2 ) ) y i ∑ i = 1 10 ( 1 − μ i ( 2 ) ) = 0.6 c^{(2)}=\frac{\sum_{i=1}^{10}(1-\mu_i^{(2)})y_i}{\sum_{i=1}^{10}(1-\mu_i^{(2)})}\\ =0.6 c(2)=∑i=110(1−μi(2))∑i=110(1−μi(2))yi=0.6
-
因为
a ( 1 ) = a ( 2 ) , b ( 1 ) = b ( 2 ) , c ( 1 ) = c ( 2 ) a^{(1)}=a^{(2)},b^{(1)}=b^{(2)},c^{(1)}=c^{(2)} a(1)=a(2),b(1)=b(2),c(1)=c(2)
即达到的平衡,所以
a ^ = 0.5 , b ^ = 0.6 , c ^ = 0.6 \hat a=0.5,\hat b=0.6,\hat c=0.6 a^=0.5,b^=0.6,c^=0.6
-
-
7.7 EM算法实现
目标:估算两个正态分布的均值(方差相同),但现在1000条数据混在了一起
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
isdebug=False
- 创建数据
#指定k个高斯分布参数,这里指定k=2,注意2个高斯分布具有同样均方差Sigma,均值分别为Mu1,Mu2
def int_data(Sigma,Mu1,Mu2,k,N):global Xglobal Muglobal ExpectationsX=np.zeros((1,N))Mu=np.random.random(2)#随机初始化均值Expectations=np.zeros((N,k))for i in range(0,N):if np.random.random(1)>0.5:X[0,i]=np.random.normal()*Sigma+Mu1#normal:从正态分布中抽取随机样本else:X[0,i]=np.random.normal()*Sigma+Mu2
#最终生成的X中的数据是两个分布混合的数据,我们并不知道数据是来自哪个分布
- 步骤1:E步
E [ i ] [ j ] = P ( x = x i ∣ μ = μ = j ) P ( x = x i ) = e − 1 2 σ 2 ( x i − μ j ) 2 ∑ i = 1 k e − 1 2 σ 2 ( x i − μ j ) 2 = N u m b e r D e n o m E[i][j]=\frac{P(x=x_i|\mu=\mu=j)}{P(x=x_i)}\\ =\frac{e^{-\frac{1}{2\sigma^2}(x_i-\mu_j)^2}}{\sum_{i=1}^ke^{-\frac{1}{2\sigma^2}(x_i-\mu_j)^2}}\\ =\frac{Number}{Denom} E[i][j]=P(x=xi)P(x=xi∣μ=μ=j)=∑i=1ke−2σ21(xi−μj)2e−2σ21(xi−μj)2=DenomNumber
#EM算法:步骤1,计算E[zij]
def e_step(Sigma,k,N):global Xglobal Muglobal Expectationsfor i in range(0,N):Denom=0for j in range(0,k):Denom+=math.exp((-1/(2*(float(Sigma**2))))*(float(X[0,i]-Mu[j]))**2)for j in range(0,k):Numer=math.exp((-1/(2*(float(Sigma**2))))*(float(X[0,i]-Mu[j]))**2)Expectations[i,j]=Numer/Denom
- 步骤2:M步
μ j = ∑ i = 1 n E x p e c t a t i o n s [ z i j ] x j ∑ i = 1 n E x p e c t a t i o n s [ z i j ] = N u m e r D e n o m \mu_j=\frac{\sum_{i=1}^nExpectations[z_{ij}]x_j}{\sum_{i=1}^nExpectations[z_{ij}]}\\ =\frac{Numer}{Denom} μj=∑i=1nExpectations[zij]∑i=1nExpectations[zij]xj=DenomNumer
#EM算法:步骤2,求最大化E[zij]的参数Mu
def m_step(k,N):global Expectationsglobal Xfor j in range(0,k):Numer=0Denom=0for i in range(0,N):Numer+=Expectations[i,j]*X[0,i]Denom+=Expectations[i,j]Mu[j]=Numer/Denom
- 算法运行
#算法迭代iter_num次,或达到精度Epsilon停止迭代
def run(Sigma,Mu1,Mu2,k,N,iter_num,Epsilon):#Sigma方差,iter_num迭代次数,Mu1和Mu2是生成数据的均值#N样本数int_data(Sigma,Mu1,Mu2,k,N)print(u"初始<u1,u2>:",Mu)for i in range(iter_num):Old_Mu=copy.deepcopy(Mu)#深拷贝e_step(Sigma,k,N)m_step(k,N)print(i,Mu)if sum(abs(Mu-Old_Mu))<Epsilon:break
if __name__=='__main__':run(6,40,20,2,1000,100,0.0001)plt.hist(X[0,:],50)plt.show()
- 运行结果
初始<u1,u2>: [0.29065113 0.21786728]
0 [30.60448153 30.32328553]
1 [31.01065788 29.92567547]
2 [32.52251613 28.41379168]
3 [36.79745623 24.13331471]
4 [40.10662972 20.77667049]
5 [40.47241312 20.351192 ]
6 [40.48060384 20.31459203]
7 [40.47597691 20.30740231]
8 [40.4736702 20.30487205]
9 [40.47270634 20.30385998]
10 [40.47231156 20.30344781]
11 [40.47215027 20.30327955]
12 [40.47208441 20.30321084]
13 [40.47205751 20.30318278]

相关文章:

【机器学习第7章——贝叶斯分类器】
机器学习第7章——贝叶斯分类器 7.贝叶斯分类器7.1贝叶斯决策论7.2 朴素贝叶斯分类器条件概率的m估计 7.3 极大似然估计优点基本原理 7.4 贝叶斯网络7.5 半朴素贝叶斯分类器7.6 EM算法7.7 EM算法实现 7.贝叶斯分类器 7.1贝叶斯决策论 一个医疗判断问题 有两个可选的假设&#…...

C++ QT开发 学习笔记(3)
C QT开发 学习笔记(3) - WPS项目 标准对话框 对话框类说明静态函数函数说明QFileDialog文件对话框getOpenFileName()选择打开一个文件getOpenFileNames()选择打开多个文件getSaveFileName()选择保存一个文件getExistingDirectory()选择一个己有的目录getOpenFileUrl()选择打幵…...

【Python实战】如何优雅地实现文字 二维码检测?
前几篇,和大家分享了如何通过 Python 和相关库,自动化处理 PDF 文档,提高办公效率。 【Python实战】自动化处理 PDF 文档,完美实现 WPS 会员功能【Python实战】如何优雅地实现 PDF 去水印?【Python实战】一键生成 PDF…...

行为型设计模式3:模板方法/备忘录/解释器/迭代器
设计模式:模板方法/备忘录/解释器/迭代器 (qq.com)...
思源笔记软件的优缺点分析
在过去一年里,我用了很多款笔记,从word文档到onenote到语雀再到思源,最后坚定的选择了思源笔记 使用感受 首先是用word文档来记笔记,主要是开始时不知道笔记软件怎么好用,等到笔记越来越膨胀的时候我发现,…...

追问试面试系列:Dubbo
欢迎来到Dubbo系列,在面试中被问到Dubbo相关的问题时,大部分都是简历上写了Dubbo,或者面试官想尝试问问你对Dubbo是否了解。 本系列主要是针对面试官通过一个点就使劲儿往下问的情况。 面试官:说说你们项目亮点 好的面试官 我们这个项目的技术亮点在于采用了Spring Cloud…...

动手学深度学习V2每日笔记(卷积层)
本文主要参考沐神的视频教程 https://www.bilibili.com/video/BV1L64y1m7Nh/p2&spm_id_from333.1007.top_right_bar_window_history.content.click&vd_sourcec7bfc6ce0ea0cbe43aa288ba2713e56d 文档教程 https://zh-v2.d2l.ai/ 本文的主要内容对沐神提供的代码中个人不…...

qcom ucsi probe
ucsi glink 注册一个ucsi 设备,和pmic glink进行通信,ucsi作为pmic glink的一个client。 lkml的patch https://lkml.org/lkml/2023/1/30/233 dtsi中一般会定义 qcom,ucsi-glink 信息,用于和驱动进行匹配 static const struct of_device_id …...

flask和redis配合
对于涉及数据提交的场景,比如更新用户信息,你可能会使用POST或PUT请求。但是,这些操作通常与直接从Redis缓存中检索数据不同,因为它们可能涉及到对后端数据库或其他存储系统的修改。并且可能需要将更新后的数据同步回Redis缓存&am…...

深度学习中的早停法
早停法(Early Stopping)是一种用于防止模型过拟合的技术,在训练过程中监视验证集(或者测试集)上的损失值。具体设立早停的限制包括两个主要参数: Patience(耐心):这是指验…...

科普文:JUC系列之多线程门闩同步器CountDownLatch的使用和源码
CountDownLatch类位于java.util.concurrent包下,利用它可以实现类似计数器的功能。比如有一个任务A,它要等待其他10个线程的任务执行完毕之后才能执行,此时就可以利用CountDownLatch来实现这种功能了。 CountDownLatch是通过一个计数器来实现…...

foreach循环和for循环在PHP中各有什么优势
在PHP中,foreach循环和for循环都是用来遍历数组的常用结构,但它们各有其优势和使用场景。 foreach循环的优势 简化代码:foreach循环提供了一种更简洁的方式来遍历数组,不需要手动控制索引或指针。易于阅读:对于简单的…...

巧用casaos共享挂载自己的外接硬盘为局域网共享
最近入手了个魔改机顶盒,已经刷好了的armbian,虽然是原生的,但是我觉得挺强大的,内置了很多 常用的docker和应用,只需要armbian-software 安装就行,缺点就是emmc太小了。 买到之后第一时间装上了casaos和1p…...

标题:解码“八股文”:助力、阻力,还是空谈?
标题:解码“八股文”:助力、阻力,还是空谈? 在程序员的面试与职场发展中,“八股文”一直是一个备受争议的话题。它既是求职者展示自己技术功底的途径,也是一些公司筛选人才的标准之一。但“八股文”在实际…...

语言无界,沟通无限:2024年好用在线翻译工具推荐
随着技术的发展现在的翻译在线工具从基础词句翻译到复杂的文章翻译都不在话下。为了防止你被五花八门的工具挑花眼,我给你介绍几款我用过的便捷、高效、准确的翻译工具吧。 1.福晰翻译端 链接直通:https://www.foxitsoftware.cn/fanyi/ 这个软件支持…...

【Golang 面试 - 进阶题】每日 3 题(十八)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...

二分+dp,CF 1993D - Med-imize
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 D - Med-imize 二、解题报告 1、思路分析 对于n < k的情况直接排序就行 对于n > k的情况 最终的序列长度一定是 (n - 1) % k 1 这个序列是原数组的一个子序列 对于该序列的第一个元素࿰…...

三十种未授权访问漏洞复现 合集( 三)
未授权访问漏洞介绍 未授权访问可以理解为需要安全配置或权限认证的地址、授权页面存在缺陷,导致其他用户可以直接访问,从而引发重要权限可被操作、数据库、网站目录等敏感信息泄露。---->目录遍历 目前主要存在未授权访问漏洞的有:NFS服务&a…...
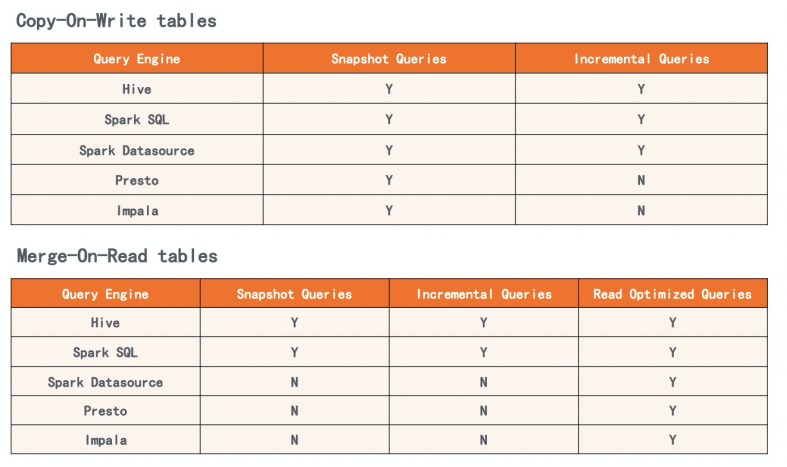
数据湖和数据仓库核心概念与对比
随着近几年数据湖概念的兴起,业界对于数据仓库和数据湖的对比甚至争论就一直不断。有人说数据湖是下一代大数据平台,各大云厂商也在纷纷的提出自己的数据湖解决方案,一些云数仓产品也增加了和数据湖联动的特性。但是数据仓库和数据湖的区别到…...

探索WebKit的奥秘:打造高效、兼容的现代网页应用
1. 简介 1.1. 主要特点 WebKit 是一个开源的浏览器引擎,它允许开发者构建高性能、功能丰富的 web 应用程序。WebKit 与 Mozilla Firefox 等使用的 Gecko 引擎、Internet Explorer 使用的 Trident 引擎以及 EdgeHTML 引擎共同构成了现代 web 浏览器的核心技术。 1.2. 学习资…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
