抽象代数精解【9】
文章目录
- 置换密码
- 密码体制
- 加解密过程
- 置换
- 置换运算
- 定义
- 置换运算的例子
- 集合与置换
- 置换规则
- 两行表示法
- 轮换表示法
- 置换运算的结果
- 置换的性质
- 注意事项
- 分组
- 加解密
- 理论基础
- 1. 准备工作
- 2. 置换过程
- 3. 置换密码的具体实现方式
- 4. 安全性分析
- 5. 置换密码的应用
- 代换密码
- 代换密码的工作原理
- 代换密码的类型
- 代换密码的应用
- 结论
- 代换与置换的区别
- 加密原理
- 实现方式
- 安全性
- 应用场景
- 总结
- 置换集合概述
- 一、定义
- 二、表示法
- 三、特殊置换
- 四、应用
- 五、实例
- 六、结论
- 哈希HASH
- 基础
- 理论
- 概述
- `hash` 函数的主要特性:
- 常见的 `hash` 函数:
- 应用场景:
- 注意事项:
- MD5
- 一、初始化
- 二、填充消息
- 三、分组处理
- 四、四轮运算
- 五、输出结果
- 注意事项
- 参考文献
置换密码
密码体制
加解密过程
- 令m为一个正整数
P = C = ( Z 26 ) m , K 是定义在集合 ( 1 , 2 , . . , m ) 上的置换组成。 P=C=(Z_{26})^m,K是定义在集合(1,2,..,m)上的置换组成。 P=C=(Z26)m,K是定义在集合(1,2,..,m)上的置换组成。
对任意的密钥(即置换) π ,定义加密: 对任意的密钥(即置换)\pi,定义加密: 对任意的密钥(即置换)π,定义加密:
e π ( x 1 , x 2 , . . . , x m ) = ( x π ( 1 ) , x π ( 2 ) , . . . , x π ( m ) ) e_{\pi}(x_1,x_2,...,x_m)=(x_{\pi(1)},x_{\pi(2)},...,x_{\pi(m)}) eπ(x1,x2,...,xm)=(xπ(1),xπ(2),...,xπ(m))
定义解密: 定义解密: 定义解密:
d π ( y 1 , y 2 , . . . , y m ) = ( y π − 1 ( 1 ) , y π − 1 ( 2 ) , . . . , y π − 1 ( m ) ) d_{\pi}(y_1,y_2,...,y_m)=(y_{\pi^{-1}(1)},y_{\pi^{-1}(2)},...,y_{\pi^{-1}(m)}) dπ(y1,y2,...,ym)=(yπ−1(1),yπ−1(2),...,yπ−1(m)) - 对于英文字母26个来说, Z 26 够用 但实际对于一个字节数据来说,需要将运算定义在群 Z 256 中。 Z_{26}够用 \\但实际对于一个字节数据来说,需要将运算定义在群Z_{256}中。 Z26够用但实际对于一个字节数据来说,需要将运算定义在群Z256中。
置换
实质是位置置换,不是内容置换,特别注意!!
置换运算
定义
1. P (明文)和 C (密文) 2. 置换运算 ( 1 ) A 是含有 n 个元素的集合 ( 2 ) S n = { π ∣ π 是 A 上的双射 } ( 3 )将 S n 中的元素称为 n 元置换。 ( 4 )现在令集合 A = { 1 , 2 , 3 , . . . , n } ,记 I ( P ) 为 P 中元素位置组成的集合, I ( C ) 为 C 中元素的位置组成的集合,则 I ( P ) = I ( C ) = A , 任意置换 π ∈ S n 表示如下: π = ( 1 2 . . . n π ( 1 ) π ( 2 ) . . . π ( n ) ) ( 5 ) S n 中有 n ! 个元素。 1.P(明文)和C(密文) \\2.置换运算 \\(1)A是含有n个元素的集合 \\(2)S_n=\{\pi|\pi是A上的双射\} \\(3)将S_n中的元素称为n元置换。 \\(4)现在令集合A=\{1,2,3,...,n\},记I(P)为P中元素位置组成的集合,I(C)为C中元素的位置组成的集合,则I(P)=I(C)=A,任意置换\pi \in S_n表示如下: \\\pi=\begin{pmatrix} 1 & 2 & ... & n \\ \pi(1) & \pi(2) & ... & \pi(n) \end{pmatrix} \\(5)S_n中有n!个元素。 1.P(明文)和C(密文)2.置换运算(1)A是含有n个元素的集合(2)Sn={π∣π是A上的双射}(3)将Sn中的元素称为n元置换。(4)现在令集合A={1,2,3,...,n},记I(P)为P中元素位置组成的集合,I(C)为C中元素的位置组成的集合,则I(P)=I(C)=A,任意置换π∈Sn表示如下:π=(1π(1)2π(2)......nπ(n))(5)Sn中有n!个元素。
置换运算的例子
本例子来自文心一言的自动生成内容
置换运算是一个将集合中的元素按照某种规则重新排列的过程。以下是一个置换运算的例子,以集合 {1, 2, 3} 为例:
集合与置换
考虑集合 S = { 1 , 2 , 3 } S = \{1, 2, 3\} S={1,2,3},我们想要对这个集合进行置换,即重新排列它的元素。
置换规则
假设我们有一个置换规则,它将集合 S S S 中的元素按照以下方式重新排列:
- 元素 1 映射到元素 2
- 元素 2 映射到元素 3
- 元素 3 映射到元素 1
这个置换可以用多种方式表示,但最常见的是通过轮换(cycle)或两行表示法(two-line notation)来表示。
两行表示法
两行表示法将原始集合的元素写在上面一行,将置换后的元素写在下面一行,并对齐:
( 1 2 3 2 3 1 ) \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} (122331)
这表示元素 1 变成了 2,元素 2 变成了 3,元素 3 变成了 1。
轮换表示法
这个置换也可以用一个轮换来表示,即 (1 2 3)。这个轮换表示元素 1 映射到 2,元素 2 映射到 3,元素 3 映射回 1,形成了一个循环。
置换运算的结果
根据这个置换规则,集合 S = { 1 , 2 , 3 } S = \{1, 2, 3\} S={1,2,3} 置换后的新集合是 S ′ = { 2 , 3 , 1 } S' = \{2, 3, 1\} S′={2,3,1}。
置换的性质
- 可逆性:每个置换都是可逆的,即存在一个逆置换可以将集合元素恢复到原始状态。在这个例子中,逆置换也是 (1 2 3)(因为它是一个 3-轮换,且 3 是奇数,所以逆置换是它本身;但在更一般的情况下,逆置换可能是不同的轮换或置换的复合)。
- 复合:两个置换可以复合成一个新的置换。例如,如果我们有另一个置换 (1 3)(将 1 映射到 3,3 映射到 1,2 保持不变),那么它与 (1 2 3) 的复合置换将是 (1 2 3) ∘ (1 3) = (2 3)(因为首先 1 变成 3,然后 3 变成 2,而 2 变成 3 后再变回 3,所以 2 保持不变,但这是一个简化的例子,实际上应该考虑所有元素的映射)。
注意事项
- 置换的复合运算不满足交换律,即 σ ∘ τ \sigma \circ \tau σ∘τ 不一定等于 τ ∘ σ \tau \circ \sigma τ∘σ(其中 σ \sigma σ 和 τ \tau τ 是两个置换)。
- 在有限集合上,所有可能的置换构成一个群,称为对称群。在这个例子中,集合 {1, 2, 3} 上的对称群 S 3 S_3 S3 包含 6 个元素:恒等置换、两个 2-轮换(即对换)和三个 3-轮换。
分组
设原文为"abcdefghij"
分组,因为m=5,所以5个字符为一组,以便下一步将每个组内部的位置进行重排,具体如下:
(1) abcde
(2) fghij
加解密
- 加密
设 m = 5 ,密钥为置换 π π = ( 1 2 3 4 5 2 4 1 5 3 ) 设m=5,密钥为置换\pi \\\pi=\begin{pmatrix} 1 & 2 & 3 &4 &5\\ 2 & 4 & 1 &5 &3 \end{pmatrix} 设m=5,密钥为置换ππ=(1224314553)
abcde=> caebd
fghij=>hfjgi - 解密 π − 1 = ( 1 2 3 4 5 3 1 5 2 4 ) \pi^{-1}=\begin{pmatrix} 1 & 2 & 3 &4 &5\\ 3 & 1 & 5 &2 &4 \end{pmatrix} π−1=(1321354254)
caebd=>abcde
hfjgi=>fghij
理论基础
置换密码(Permutation Cipher),又称为换位密码(Transposition Cipher),其工作原理主要基于重新排列明文中的字符或字节的顺序来生成密文,而不改变这些字符或字节本身的内容。以下是置换密码工作的详细过程:
1. 准备工作
- 选择密钥:密钥是置换密码中用于指导字符重新排列的关键信息。密钥可以是数字序列、字母序列或其他形式的标识符,具体形式取决于所使用的置换密码算法。
- 确定分组:根据密钥或算法的要求,将明文分成若干组或块。这些组或块的大小可以是固定的,也可以是可变的,具体取决于算法的设计。
2. 置换过程
- 字符排列:在每个组或块内,按照某种特定的置换规则(通常由密钥决定)重新排列字符的顺序。这些规则可能涉及列置换、行置换、矩阵置换等多种方式。
- 生成密文:根据置换后的字符顺序,重新组合成密文。在密文中,字符的内容保持不变,但它们的顺序已经发生了改变。
3. 置换密码的具体实现方式
- 列置换:将明文按列写入一个矩阵中,然后根据密钥指定的列顺序重新排列这些列,最后按行或按列读出以形成密文。
- 行置换:与列置换类似,但将明文按行写入矩阵,并根据密钥指定的行顺序进行重排。
- 矩阵置换:将明文中的字符按照某种规则(如密钥指定的顺序)填充到一个矩阵中,然后根据密钥提供的顺序重新组合矩阵中的字符,以形成密文。
4. 安全性分析
- 单次置换的局限性:单次置换后的密文往往保留了原始明文的某些统计特性(如字符频率分布),这使得它相对容易被破解。因此,单次置换的安全性较低。
- 多次置换的增强:为了提高安全性,可以对同一明文进行多次置换。每次置换都可以使用不同的算法或密钥,以进一步打乱字符的顺序并增加破解的难度。
5. 置换密码的应用
- 置换密码在古典密码学中有着广泛的应用,如历史上的栅栏密码等。
- 在现代密码学中,置换密码的概念仍然被用于某些加密算法中,但通常作为加密过程的一部分而非唯一手段。
综上所述,置换密码通过重新排列明文中的字符顺序来生成密文,其工作原理简单而有效。然而,为了确保加密的安全性,通常需要结合其他加密方法共同使用。
代换密码
代换密码(Substitution Cipher),又称为代替密码或替代密码,是密码学中的一种基本加密方法。它通过替换明文中的字符(如字母、数字或符号)来生成密文,从而保障信息的安全性。代换密码的加密过程通常涉及一个代换表(也称为密钥),该表定义了明文字符与密文字符之间的映射关系。
代换密码的工作原理
-
建立代换表:首先,根据密钥信息(可能是数字、字母序列或其他形式的标识符)建立一个代换表。这个表定义了如何将明文中的每个字符替换为密文中的对应字符。
-
加密过程:在加密过程中,将明文中的每个字符依次通过代换表进行查找和替换,生成密文。这个过程中,明文字符的内容发生了改变,但它们的顺序保持不变。
-
解密过程:解密是加密的逆过程。在解密时,使用相同的代换表(即密钥)将密文中的每个字符替换回明文中的对应字符,从而恢复出原始信息。
代换密码的类型
代换密码可以分为两大类:单表代换密码和多表代换密码。
-
单表代换密码:
- 单表代换密码是指对明文消息中出现的同一个字母,在加密时都使用同一固定的字母来代换,不管它出现在什么地方。
- 常见的单表代换密码包括凯撒密码(Caesar Cipher),它将明文中每个字母都按照字母表顺序向后(或向前)移动若干个位置来生成密文。
- 优点:实现简单,易于理解。
- 缺点:安全性较低,容易受到频率分析等攻击。
-
多表代换密码:
- 多表代换密码是指明文消息中出现的同一个字母,在加密时不是完全被同一固定的字母代换,而是根据其出现的位置次序,用不同的字母代换。
- 常见的多表代换密码包括维吉尼亚密码(Vigenère Cipher)和Playfair密码。维吉尼亚密码是一种典型的多表密码,它使用一个密钥字符串对明文进行加密,每个明文字符都与密钥字符串中对应位置的字符结合进行加密。Playfair密码则是一种基于两字母组的代替密码,它使用一个5阶方阵作为密钥,根据一定的规则对明文中的字母对进行加密。
- 优点:能够更好地抵抗统计密码分析,提高加密的安全性。
- 缺点:如果密钥长度较短或重复使用,仍然可能受到攻击。
代换密码的应用
代换密码在密码学历史上有着广泛的应用,从古典密码学时期的各种代换密码算法,到现代密码学中的某些加密算法(如某些对称加密算法中的S盒设计),都可以看到代换密码的影子。此外,代换密码也是密码学教学和研究中的一个重要内容,它有助于人们理解密码学的基本原理和加密方法。
结论
代换密码是一种基于字符替换的加密方法,它通过代换表将明文中的字符替换为密文中的对应字符来生成密文。代换密码可以分为单表代换密码和多表代换密码两大类,它们在安全性、实现复杂度和应用场景等方面各有特点。在实际应用中,可以根据需要选择合适的代换密码算法来保护信息的安全性。
代换与置换的区别
置换密码(Permutation Cipher)和代换密码(Substitution Cipher)是密码学中的两种基本加密方法,它们在加密原理、实现方式和安全性方面存在明显的区别。
加密原理
- 置换密码:通过重新排列明文中的字符或字节的顺序来生成密文,而不改变这些字符或字节本身的内容。其核心在于改变字符的位置,而非内容。
- 代换密码:通过替换明文中的字符(如字母、数字或符号)来生成密文。每个明文字符都被映射到密文中的另一个字符,而字符的顺序保持不变。
实现方式
- 置换密码:
- 常见的实现方式包括列置换、行置换和矩阵置换等。
- 明文被分成若干组或块,然后根据密钥或算法的要求重新排列这些组或块中的字符顺序。
- 代换密码:
- 通过建立代换表(也称为密钥)来实现加密。
- 明文中的每个字符都在代换表中查找对应的密文字符,并进行替换。
安全性
- 置换密码:
- 单次置换可能保留了原始明文的某些统计特性(如字符频率分布),因此相对容易被识别和分析。
- 通过多次置换或与其他加密方法结合使用,可以显著提高安全性。
- 代换密码:
- 单表代换密码的安全性较低,容易受到频率分析等攻击。
- 多表代换密码通过引入更多的变换规则,提高了安全性,但仍需注意密钥的管理和安全性。
应用场景
- 置换密码:由于其实现简单且易于理解,常用于教学或演示目的。在需要较高安全性的场合,通常与其他加密方法结合使用。
- 代换密码:在历史上有着广泛的应用,如凯撒密码等。在现代密码学中,代换密码的思想仍然被用于某些加密算法中(如对称加密算法中的S盒设计)。
总结
置换密码和代换密码在加密原理、实现方式和安全性方面存在明显的区别。置换密码通过重新排列字符顺序来加密,而代换密码则通过替换字符来加密。在实际应用中,可以根据需要选择合适的加密方法或结合使用多种加密方法来提高信息的安全性。
置换集合概述
下面内容来自文心一言的自动生成内容
置换集合是一个数学概念,尤其在集合论、抽象代数以及组合数学中有重要的应用。以下是对置换集合的详细解释:
一、定义
- 集合的置换:集合的置换是指从集合到其自身的双射(即一一映射),也就是说,集合中的每一个元素都唯一地映射到集合中的另一个元素,且没有元素被遗漏。
- 有限集合的置换:对于有限集合X,其置换的个数恰好是X中元素个数的阶乘(n!),其中n是集合X中元素的个数。
二、表示法
- 矩阵表示法:在有限集的情况下,可以利用矩阵符号将自然排序写在第一列,而将置换后的排序写在第二列来表示置换。
- 轮换分解:另一种表示方法是借由置换的相继作用描述,这被称为“轮换分解”。轮换是将集合中的一些元素循环移位,而保持其他元素不变。
三、特殊置换
- 对换:长度为二的轮换称为对换,即只交换两个元素的位置,而保持其他元素不变。
- 奇置换与偶置换:根据置换可以分解为偶数个还是对数个对换,置换被分为奇置换和偶置换。
四、应用
- 对称群:集合X的全体置换构成一个群,称为X上的对称群,记为S_X。当X={1,2,…,n}时,常用S_n来记S_X,并称之为n个字母上的对称群。
- 计算机科学:在计算机学科中,置换的概念被用于各种算法和数据结构中,特别是在处理排列、组合和排序问题时。
五、实例
考虑集合X={1,2,3},其置换有6个,分别是:
- 123(恒等置换)
- 132
- 213
- 231
- 312
- 321
这些置换可以看作是集合X中元素的一种重排方式。
六、结论
置换集合是数学中的一个基本概念,它描述了集合中元素位置互换的可能性。在有限集合的情况下,置换的个数是有限的,并且与集合中元素的个数密切相关。置换的概念在抽象代数、组合数学以及计算机科学等领域都有广泛的应用。
哈希HASH
基础
- 带密钥的HASH族
满足以下条件的四元组 X , Y , K , H X,Y,K,H X,Y,K,H
X:所有可能消息的集合
Y:所有可能的消息摘要或认证标签构成的有限集
K:密钥空间,所有可能的密钥构成的有限集
∀ k ∈ K , H A S H 函数 h K ∈ H , h k : X → Y \forall k \in K,HASH函数h_K \in H,h_k:X\rightarrow Y ∀k∈K,HASH函数hK∈H,hk:X→Y
理论
概述
hash 函数是一种将任意长度的输入(通常称为“消息”或“键值”)通过某种算法转换成固定长度输出(通常是一个较小的数值)的过程。这个固定长度的输出被称为“哈希值”或“散列值”。hash 函数在计算机科学中有广泛的应用,包括但不限于数据加密、数据索引、快速查找、错误检测、数据去重等领域。
hash 函数的主要特性:
- 确定性:相同的输入必定产生相同的输出。
- 单向性:通常很难(理想情况下是不可能)从哈希值推导出原始输入值。
- 碰撞抵抗性:理想情况下,不同的输入产生相同输出的可能性极低(但并非绝对不可能)。
- 高效性:计算哈希值的过程应当快速高效。
常见的 hash 函数:
- MD5:一种广泛使用的哈希函数,产生128位(16字节)的哈希值。但由于其存在碰撞问题,已不推荐用于安全相关的场合。
- SHA(Secure Hash Algorithm):包括多个版本,如SHA-1、SHA-2(包括SHA-256、SHA-512等)、SHA-3等。SHA-1产生的哈希值是160位(20字节),而SHA-256产生的是256位(32字节)的哈希值。SHA系列函数因其较高的安全性被广泛用于安全领域。
- CRC(Cyclic Redundancy Check):虽然CRC主要用于错误检测而非安全目的,但它也可以看作是一种哈希函数。它通过多项式除法来计算哈希值,常用于文件传输或存储中检测数据是否损坏。
- BLAKE2:一种快速的加密哈希函数,旨在改进现有哈希函数的性能,同时保持高安全性。
应用场景:
- 密码存储:存储密码的哈希值而非明文密码,即使数据库被泄露,攻击者也难以直接获取密码。
- 数据完整性校验:通过计算文件的哈希值来验证文件在传输或存储过程中是否被篡改。
- 快速查找:通过哈希表实现快速的数据查找、插入和删除操作,哈希表使用哈希函数将键值映射到表的索引位置。
注意事项:
- 不同的哈希函数适用于不同的场景,选择时应根据具体需求进行。
- 尽量避免使用已被证明存在安全漏洞的哈希函数,如MD5和SHA-1(在安全性要求较高的场合)。
- 考虑到哈希碰撞的可能性,虽然很低,但在设计系统时仍需考虑其潜在影响。
MD5
MD5(Message-Digest Algorithm 5,消息摘要算法第5版)是一种广泛使用的散列函数,能够产生一个128位的散列值(通常以32个十六进制数表示),主要用于确保信息传输的完整性和一致性。以下是MD5算法过程的详细描述:
一、初始化
- 设置初始值:MD5算法使用四个32位的缓存变量(或称为幻数)A、B、C、D,这些变量在算法开始前被初始化为特定的整数值。按照RFC 1321标准,这些初始值在十六进制下表示为:
- A = 0x67452301
- B = 0xEFCDAB89
- C = 0x98BADCFE
- D = 0x10325476
二、填充消息
- 计算填充长度:计算输入消息的长度(以位为单位)对512求余的结果。如果余数不等于448,则需要进行填充,使得填充后的总长度对512求余的结果为448。
- 填充操作:
- 在消息末尾首先填充一个1。
- 然后填充0,直到长度满足上述条件。
- 最后,在消息的末尾附加上64位(8字节)的消息原始长度(也是以位为单位),这样消息的总长度就变为(N+1)*512。
三、分组处理
- 分组:将填充后的消息按512位(64字节)进行分组,每个分组再被划分为16个32位的子分组(即M0到M15)。
- 循环处理:对每个分组执行四轮(共64步)的复杂非线性操作,每一轮使用不同的非线性函数(F、G、H、I)和常量,以及左移操作。
四、四轮运算
四轮运算中,每一轮都使用特定的非线性函数和常量,以及左移操作来更新A、B、C、D这四个变量。每轮运算包含16个步骤,每个步骤都涉及当前变量、上一个步骤的输出、当前子分组以及一个常量。以下是四轮运算的简要描述:
- 第一轮:使用函数F和特定的常量,进行16次操作。
- 第二轮:使用函数G和另一组常量,进行16次操作。
- 第三轮:使用函数H和另一组常量,进行16次操作。
- 第四轮:使用函数I和最后一组常量,进行16次操作。
五、输出结果
- 连接变量:四轮运算完成后,将A、B、C、D这四个32位变量按顺序连接起来,形成一个128位的散列值。
- 表示散列值:这个128位的散列值通常以32个十六进制数的形式表示,每个十六进制数占4位。
注意事项
- MD5算法是一种单向加密算法,即只能对明文进行加密生成散列值,而不能通过散列值逆向得到明文。
- 尽管MD5算法在数据加密和安全校验方面有着广泛的应用,但由于其存在哈希碰撞的问题,即不同的输入可能产生相同的输出,因此在安全性要求较高的场合,已逐渐被SHA-2和SHA-3等更安全的算法所取代。
以上信息基于MD5算法的原理和广泛认可的文档(如RFC 1321)进行描述,确保了准确性和权威性。
参考文献
1.《密码学原理与实践(第三版)》
2. 文心一言
相关文章:

抽象代数精解【9】
文章目录 置换密码密码体制加解密过程置换置换运算定义置换运算的例子集合与置换置换规则两行表示法轮换表示法置换运算的结果置换的性质注意事项 分组加解密 理论基础1. 准备工作2. 置换过程3. 置换密码的具体实现方式4. 安全性分析5. 置换密码的应用代换密码代换密码的工作原…...

熟悉简单测试面经
SQL语句中增、删、查、改的关键字 MySQL中SQL语句删除语句有哪些?区别是啥。 “”和equals的区别 “String s "1"”与“String s new String("1")”中的s一样吗? StringBuilder与StringBuffer的区别 洗牌问题 HTTP、HTTPS、U…...

IoTDB 入门教程 实战篇④——C#示例(开源)
文章目录 一、前文二、新建C#项目三、NuGet安装四、示例源码五、查询数据六、参考 一、前文 IoTDB入门教程——导读 本文详细阐述了如何通过一个C#项目成功连接到IoTDB时序数据库,进而展示了如何向该数据库高效地写入数据以及执行精确的数据查询操作。 此示例旨在为…...

STL-vector容器
目录 一、常见接口 1.1 构造函数 1.2 访问与遍历 1.3 容量操作 1.4 增删查改 二、模拟实现 2.1 迭代器失效 2.2 源代码 一、常见接口 vector数据结构实际上是顺序表 详细解释与使用请参见官方网站:vector - C Reference (cplusplus.com) 1.1 构造函数 函…...

python字符串与变量名互相转换,字典,list操作
locals是python的内置函数,他可以以字典的方式去访问局部和全局变量 vars()本函数是实现返回对象object的属性和属性值的字典对象 eval()将字符串str当成有效的表达式来求值并返回计算结果 #!/usr/bin/python3 #-*- coding uft-8 -*- guo 666 str1 "guo&qu…...

企业及园区电力能源管理系统方案
概述 面对中小型的用能集团、园区能耗监测分析等场景需求,拓扑未来公司推出标准化的企业及园区电力能源管理系统方案,力求高效高质地为目标客户提供高效部署、轻松运维的本地化能源管理解决方案。 本方案以软硬件一体的方式,集成了标准电力监…...

5.3 需求分析
需求分析 软件需求定义分类练习题 需求工程需求获取练习题 需求分析状态转化图数据流图DFD顶层数据流图0层数据流图1层数据流图 练习题 需求规约需求定义方法 需求验证需求管理版本控制需求跟踪变更控制练习题 考试大概3分 软件需求 定义 软件需求:是指用户对目标…...
)
【C++】list介绍以及模拟实现(超级详细)
欢迎来到我的Blog,点击关注哦💕 list的介绍和模拟实现 前言list介绍标准库容器 std::list 与 std::vector 的优缺点缺点 list的基本操作构造函数list iteratorlist capcacitylist modify list模拟实现存贮结构(双向带头循环)itera…...
从艺术创作到作物生长,农业AI迎来“GPT“时刻
(于景鑫 国家农业信息化工程技术研究中心)"GPT"一词早已不再神秘,其在文本、图像生成领域掀起的风暴正以摧枯拉朽之势席卷全球。人们惊叹于ChatGPT对话之智能、思维之敏捷,更对Stable Diffusion、Midjourney创作的艺术画作赞叹不已。而大语言模…...

前端使用 Konva 实现可视化设计器(19)- 连接线 - 直线、折线
本章响应小伙伴的反馈,除了算法自动画连接线(仍需优化完善),实现了可以手动绘制直线、折线连接线功能。 请大家动动小手,给我一个免费的 Star 吧~ 大家如果发现了 Bug,欢迎来提 Issue 哟~ github源码 gitee…...

C#:通用方法总结—第15集
大家好,今天继续分享我们的通用方法系列。 下面是今天的通用方法: (1)这个通用方法为用文件流写数据 /// <summary> /// 用文件流写数据 /// </summary> /// <param name"data"></param> //…...

LoadRunner12 添加事务并添加检查点
1、先要添加事务开始函数lr_start_transaction("登陆事务");,在接口上方右击点击-插入-开始事务。输入事务名称; 2、在某个接口想法 右击点击-插入-结束事务,输入事务名称,与开始事务名称要保持一致,lr_end_…...

python中的文件
绝对路径和相对路径 一般情况下绝对路径就是从根目录开始描述的路径 相对路径就是相对于当前目录 . 没错,就是一个点,表示的是当前文件夹;.. 两个点表示的是上一层文件夹 os模块与os.path os 和 os.path 是两个非常重要的标准库模块,它们分别用于操作系统相关的功能操…...

Powerdesigner连接mysql数据库,逆向工程生成ER图 (保姆级教程:下载->连接->配置)看这一篇就够了
一、下载powerdesigner 下载的教程请看如下链接,我太懒了,直接借鉴! 把别大佬的博客搬过来了嘿嘿~我真聪明!ㄟ( ▔, ▔ )ㄏ 操作到完成汉化就好!!第5步不看了,别按那个走,因为新手…...

商家转账到零钱分销返佣申请方案及驳回处理办法
分销返佣场景是商家申请最多的场景,因而申请被驳回也是最多的,根据我们上万次成功开通商家转账到零钱的经验,当商家转账到零钱的分销返佣场景被驳回时,按照以下步骤,商家都可以快速过审: 一、分析驳回原因 …...

荟萃科技:国外问卷调查有没有实时更新的题库?
有的,口子查和渠道查都是。 口子查的题目都是国外的公司发放在网络上,都是实时发布,所以我们需要去国外的各大社交平台做题。 这些题目不是集中的,而是散布在网站里面,需要我们去找,都是老外上班实时发放…...

【课程总结】Day18:Seq2Seq的深入了解
前言 在上一章【课程总结】Day17(下):初始Seq2Seq模型中,我们初步了解了Seq2Seq模型的基本情况及代码运行效果,本章内容将深入了解Seq2Seq模型的代码,梳理代码的框架图、各部分组成部分以及运行流程。 框…...

C++利用开发人员命令提示工具查看对象模型
1.跳转文件路径 cd 具体路径 2.输入c1 /d1 reportSingleClassLayout类名 文件名 操作示例如下图:...

白骑士的PyCharm教学高级篇 3.4 服务器部署与配置
系列目录 上一篇:白骑士的PyCharm教学高级篇 3.3 Web开发支持 在开发完成后,将代码部署到服务器上是一个关键步骤。PyCharm不仅提供了强大的本地开发支持,还为远程服务器配置与部署、自动化部署流程提供了便捷的工具和功能。本文将详细介绍如…...
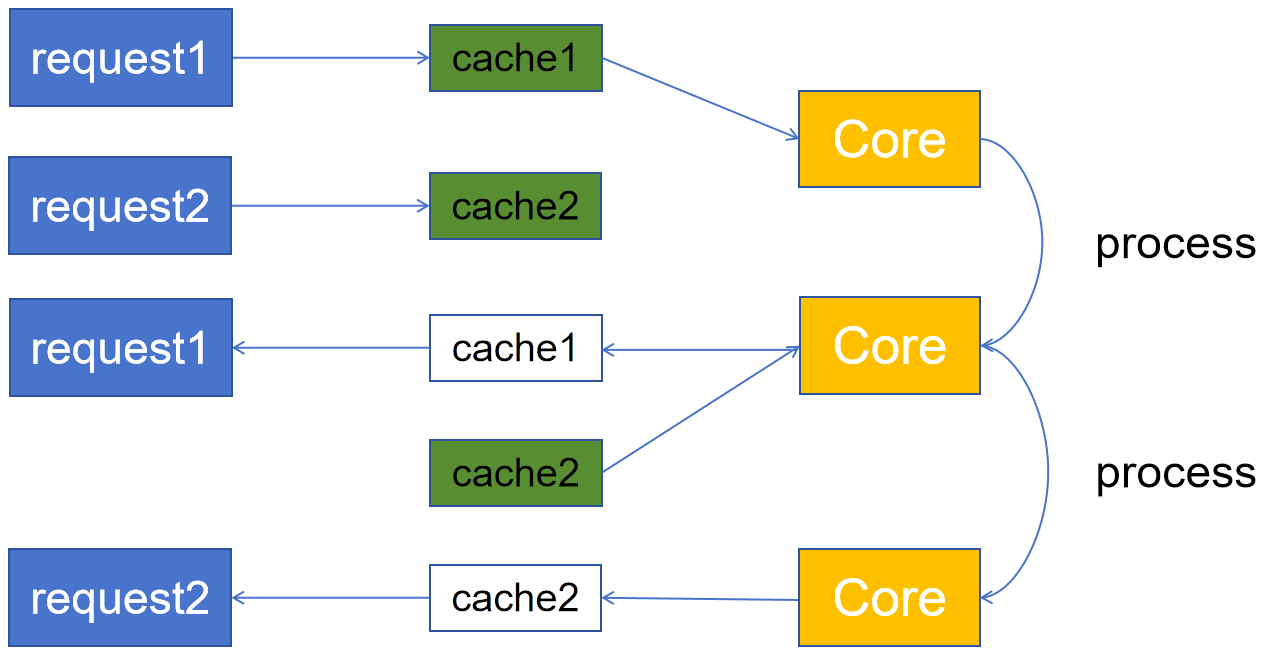
数据库管理-第226期 内存至超线程(20240805)
数据库管理226期 2024-08-05 数据库管理-第226期 内存至超线程(20240805)1 CPU内缓存结构2 缓存与内存3 单核单线程4 超线程5 超线程的利弊总结 数据库管理-第226期 内存至超线程(20240805) 作者:胖头鱼的鱼缸…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...
生成对抗网络(GAN)损失函数解读
GAN损失函数的形式: 以下是对每个部分的解读: 1. , :这个部分表示生成器(Generator)G的目标是最小化损失函数。 :判别器(Discriminator)D的目标是最大化损失函数。 GAN的训…...

小白的进阶之路系列之十四----人工智能从初步到精通pytorch综合运用的讲解第七部分
通过示例学习PyTorch 本教程通过独立的示例介绍PyTorch的基本概念。 PyTorch的核心提供了两个主要特性: 一个n维张量,类似于numpy,但可以在gpu上运行 用于构建和训练神经网络的自动微分 我们将使用一个三阶多项式来拟合问题 y = s i n ( x ) y=sin(x) y=sin(x),作为我们的…...

【图片转AR场景】Tripo + Blender + Kivicube 实现图片转 AR 建模
总览 1.将 2D 图片转为立体建模 2. 3. 一、将 2D 图片转为立体建模 1.工具介绍 Tripo 网站 2.找图片 找的图片必须是看起来能够让 AI 有能力识别和推理的,因为现在的AI虽然可以补全但是能力还没有像人的想象力那么丰富。 比如上面这张图片,看起来虽…...

C#调用Rust动态链接库DLL的案例
C#调用Rust动态链接库DLL的案例 项目概述 这是一个演示C#调用Rust动态链接库DLL的项目,包含: C#主程序 (Program.cs)Rust动态链接库 (rust_to_csharp目录) 使用C#创建一个net9的控制台项目,不使用顶级语句 dotnet new console --framewo…...
