uniapp获取swiper中子组件的内容高度
swiper有默认高度,如果不单独设置一个具体高度，swiper后面的内容将不会展示
这里展示的例子是: swiper中放有一个子组件,想要完整展示子组件的内容，swiper就需要获取到子组件的内容高度并设置
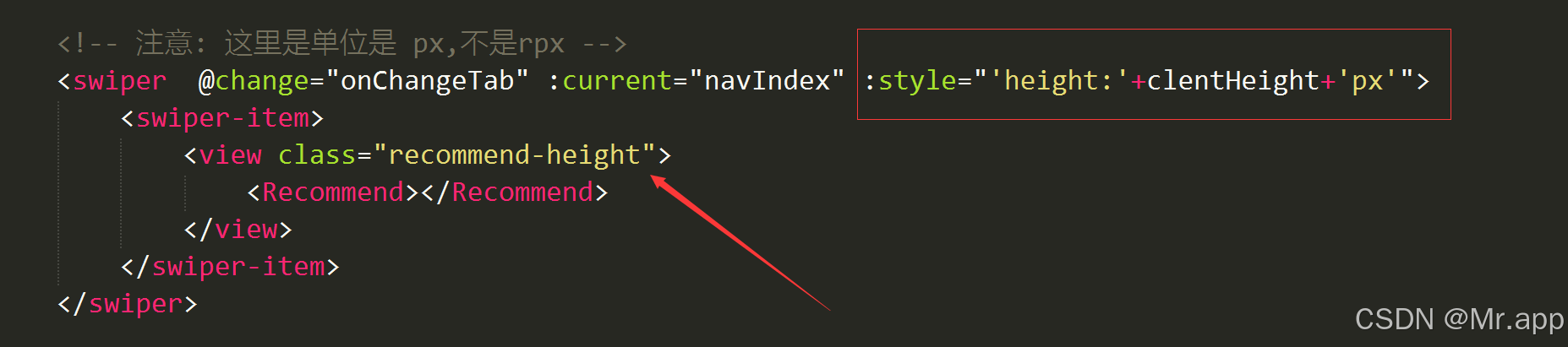
<!-- 注意: 这里的单位是 px,不是rpx --><swiper @change="onChangeTab" :current="navIndex" :style="'height:'+clentHeight+'px'"><swiper-item><view class="recommend-height"><Recommend></Recommend> </view></swiper-item> </swiper>
// 获取swiper内容的整体高度 onReady() { let view = uni.createSelectorQuery().select('.recommend-height')view.boundingClientRect((data) => {this.clentHeight = data.heightconsole.log(data.height)}).exec()},
相关文章：
uniapp获取swiper中子组件的内容高度
swiper有默认高度,如果不单独设置一个具体高度，swiper后面的内容将不会展示 这里展示的例子是: swiper中放有一个子组件,想要完整展示子组件的内容，swiper就需要获取到子组件的内容高度并设置 <!-- 注意: 这里的单位是 px,不是rpx --><swiper…...
基于计算机爱心小屋公益机构智慧管理(源码+论文+部署讲解等)
博主介绍： ✌我是阿龙，一名专注于Java技术领域的程序员，全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师，我在计算机毕业设计开发方面积累了丰富的经验。同时，我也是掘金、华为云、阿里云、InfoQ等平台的优…...
详细学习PyQt5的样式表与界面美化
Pyqt5相关文章: 快速掌握Pyqt5的三种主窗口 快速掌握Pyqt5的2种弹簧 快速掌握Pyqt5的5种布局 快速弄懂Pyqt5的5种项目视图（Item View） 快速弄懂Pyqt5的4种项目部件（Item Widget） 快速掌握Pyqt5的6种按钮 快速掌握Pyqt5的10种容器&…...
遥控器android设备键值原理
输入设备触发事件发送数据-》将键值映射到内核中预定义的键值-》上报键值，通过kl文件将按键码转化为标签字符串 内核获取键码，扫描码 按键标签其实对应的也是一个按键码。与kernel上报的按键码不同，按键标签所对应的按键…...
零基础也想学编程？Java零基础入门学习路线 + Java教程已准备好！
本文作者：程序员鱼皮 免费编程学习 - 编程导航网：https://www.code-nav.cn 符号表 可以通过路线知识点前的表情字符，根据自己的实际情况选择学习： 🌕 所有同学必须学习！！！…...
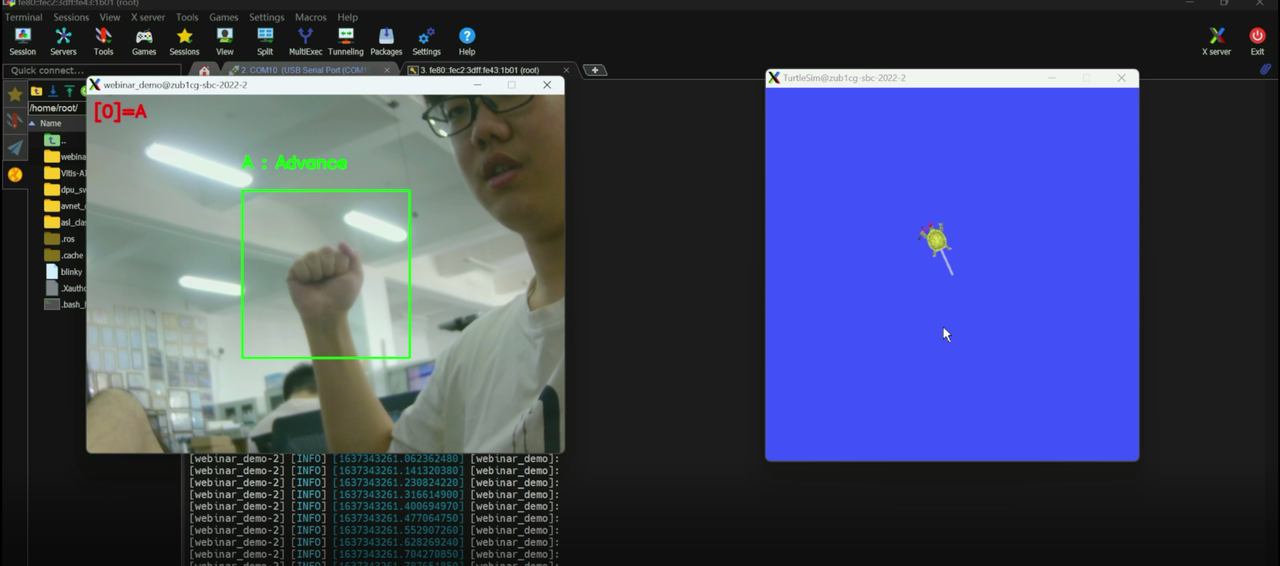
Avnet ZUBoard 1CG开发板上手—深度学习新选择
Avnet ZUBoard 1CG 开发板上手—深度学习新选择 摘要 本文主要介绍了 Avnet ZUBoard 1CG 开发板的特性、架构、硬件单元等概念，并对如何使用以太网接口和串口连接开发板进行基本介绍，同时辅以两个应用例程演示其功能。 原文链接： FreakSt…...
C/C++复习 day1
C/C复习 day1 文章目录 C/C复习 day1前言一、C语言1.memcpy函数2.memmove函数3.strstr函数4.宏定义的函数5.大小端的介绍以及判断 二、C入门基础1.C是如何支持函数重载的？2.建议用const enum inline去替代宏 三、C类和对象1.类大小的计算2.移动构造和移动赋值1.右值…...
再见Figma！！新的设计,代码协作神器！【送源码】
软件介绍 Penpot 是一款专门用来帮助设计师和开发者更好地合作的软件。它可以让设计师轻松地做出漂亮的设计稿，还能让这些设计稿变成真正的网站或者应用的一部分。这样，设计师和开发者之间就不会因为沟通不畅而产生麻烦了。 Penpot 专为设计师与开发者之…...
快速拷贝复制工具软件@拷贝工具@多线程拷贝@robocopy
文章目录 refs常见复制工具高速拷贝工具特性对比 Robocopy👺Robocopy工具基本用法语法示例 常用选项常见选项列表示例 高级用法多线程复制日志记录 用例案例直接递归复制大量文件的文件夹多线程复制监视被打开文件文件数 复制时排除某个目录排除交接点跳过无法复制的…...
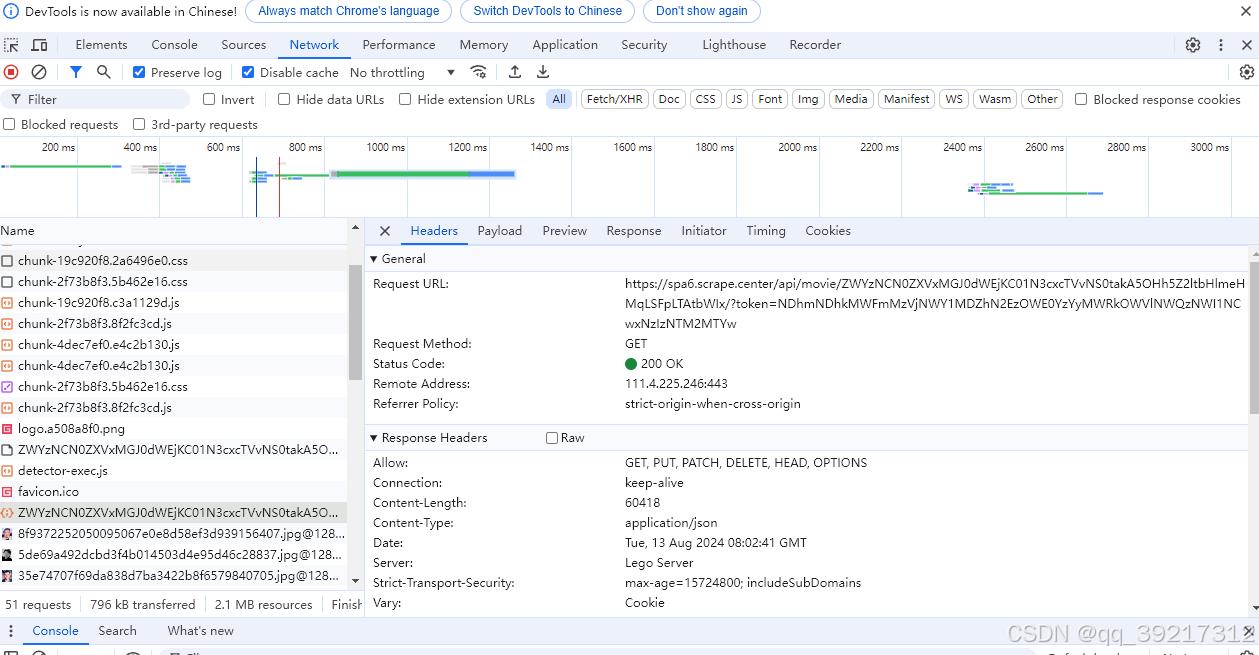
JavaScript 逆向爬取实战
准备介绍： 当我们学习完整个 JS 逆向技巧后，这里是一次完整的分析爬取实战 案例介绍 本节案例网站不仅在 API 参数有加密， 而且前端 JS 也带有压缩混淆，其前端压缩打包工具使用 webpack , 混淆工具使用 javascript-obfuscator 。…...
Vue 项目中导入文件时如何默认找寻该文件夹下的 index.vue 文件
文章目录 需求分析 需求 如下图，在Vue 项目中导入 frequencyChange 文件夹时如何默认找寻该文件夹下的 index.vue 文件 分析 确保项目结构和命名约定 首先，确保你的 Vue 单文件组件按照约定命名，例如： components/Example/inde…...
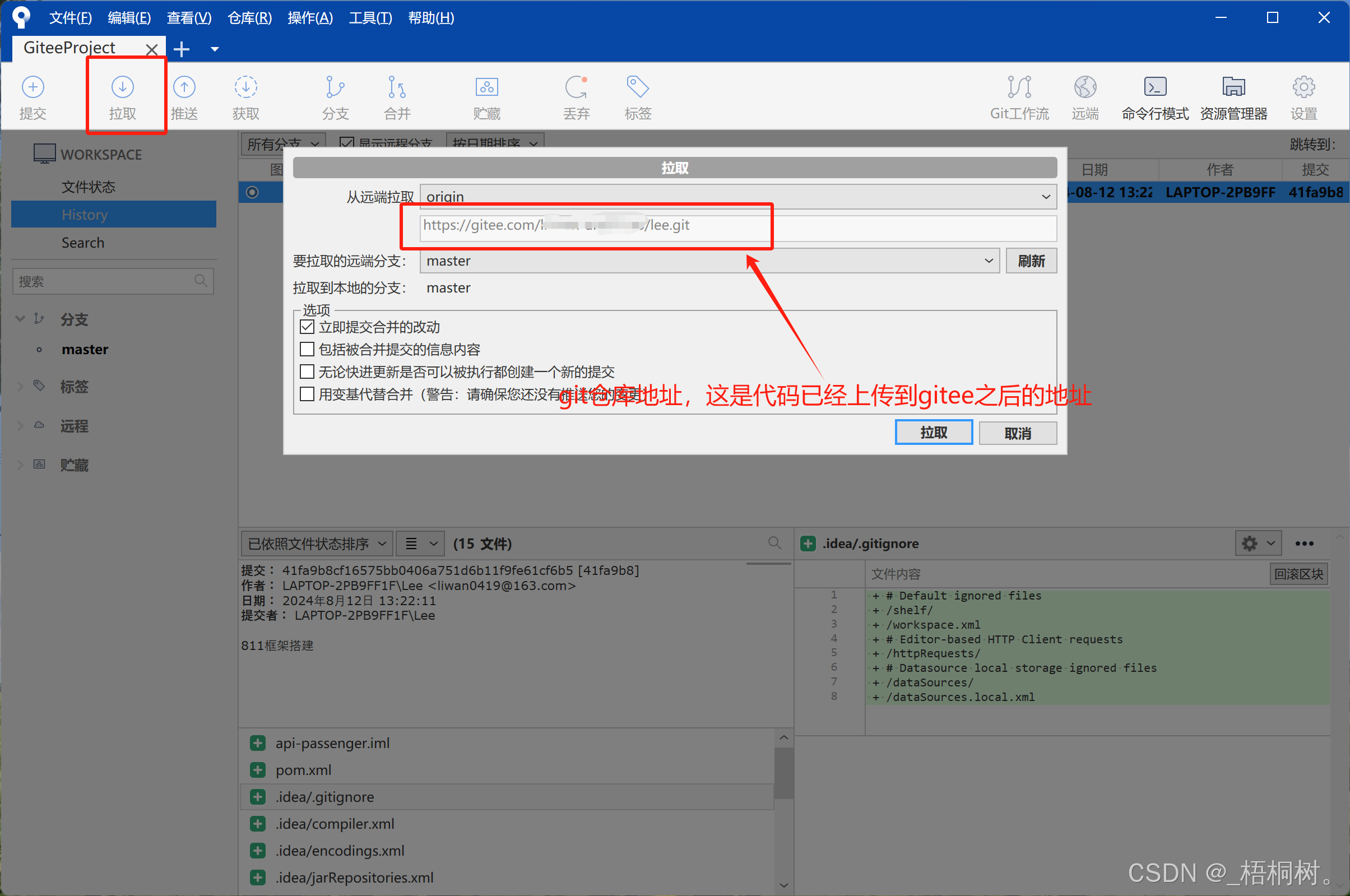
Idea2023.3.3 —— SourceTree与gitee关联
SourceTree SourceTree链接: https://pan.baidu.com/s/1oqPxhpHeNOOiuRRQydes6g?pwdngru 提取码: ngru 点击Generate 分别保存私钥和公钥 gitee官网注册 这是gitee的公钥，与上面SourceTree的公钥私钥不一样 gitee生成公钥，确保本地安装好git git链接: h…...
一文HDMI (High-Definition Multimedia Interface)
HDMI（High-Definition Multimedia Interface，高清多媒体接口）是一种紧凑的音视频接口，它能够将未压缩的视频数据以及压缩或未压缩的数字音频数据，从符合HDMI标准的源设备无缝传输到兼容的计算机显示器、视频投影仪、数…...
【HBZ分享】高并发下如何设计缓存来提升系统性能？
普通模式 普通模式即前段调用后端接口，然后后端先查缓存， 查不到的情况下再查数据库，然后把数据库中的内容放到缓存中。瓶颈：瓶颈在于tomcat的性能，一般并发可以，面临海量并发冲击，tomcat就显得…...
【AI 绘画】 文生图图生图（基于diffusers）
AI 绘画- 文生图&图生图（基于diffusers） 1. 效果展示 本次测试主要结果展示如下： SDXL文生图 可爱Lora 2. 基本原理 模型基本原理介绍如下 stable diffusion首先训练一个自编码器，学习将图像数据压缩为低维表示。通过使…...
已解决HarmonyOS模拟器卡顿问题
以下是一些可以尝试用来解决 HarmonyOS 模拟器卡顿问题的方法： 一、检查系统资源占用 关闭不必要的后台程序 在电脑上，通过任务管理器（Windows 系统中按 Ctrl Shift Esc，Mac 系统通过活动监视器）查看并关闭占用大量 …...
)
C++ | 深入理解C++中的特殊类设计和单例模式(懒汉模式、饿汉模式)
目录 特殊类设计和单例模式 1、不可拷贝类 2、只能在堆上创建对象的类 3、只能在栈上创建对象的类 4、不可继承的类 5、单例模式(懒汉模式、饿汉模式) 特殊类设计和单例模式 在C编程中，类的设计往往需要满足特定的需求和约束。特殊类设计模式提供了一种方法来…...
Java设计模式之中介者模式
Java设计模式之中介者模式 在软件开发中，设计模式是解决常见问题的最佳实践。通过运用设计模式，我们可以提高代码的可维护性、可扩展性以及可读性。今天，我们将探讨一种非常重要的行为型设计模式——中介者模式（Mediator Pattern…...
实现父组件调用子组件方法时报错：[Vue warn]: Invalid vnode type when creating vnode: null.
使用uniapp实现父组件调用子组件方法时报错：[Vue warn]: Invalid vnode type when creating vnode: null. 实现代码如下： 子组件： <template><view><view class"toolsHeader"><view class"toolsTitl…...
Java面试八股之什么是消息队列
什么是消息队列 消息队列（Message Queue）是一种应用程序间通信（IPC）的形式，它允许进程将消息发送到另一个消息队列，接收端则可以在任何时刻从队列中取出这些消息进行处理。消息队列提供了一种异步处理、解…...
（十）学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端，同时完善学生端的构建。本次工作主要包括： 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
黑马Mybatis
Mybatis 表现层：页面展示 业务层：逻辑处理 持久层：持久数据化保存 在这里插入图片描述 Mybatis快速入门 
三体问题详解
从物理学角度，三体问题之所以不稳定，是因为三个天体在万有引力作用下相互作用，形成一个非线性耦合系统。我们可以从牛顿经典力学出发，列出具体的运动方程，并说明为何这个系统本质上是混沌的，无法得到一般解…...
CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码，CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短，所以CPU会不断地切换线程执行，从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
全志A40i android7.1 调试信息打印串口由uart0改为uart3
一，概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本：2014.07； Kernel版本：Linux-3.10； 二，Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01)，并让boo…...
Map相关知识
数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...
【Go语言基础【12】】指针：声明、取地址、解引用
文章目录 零、概述：指针 vs. 引用（类比其他语言）一、指针基础概念二、指针声明与初始化三、指针操作符1. &：取地址（拿到内存地址）2. *：解引用（拿到值） 四、空指针&am…...
Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一：使用Read()读取文件2.3、方式二：bufio读取文件2.4、方式三：os.ReadFile读取2.5、写…...
解析奥地利 XARION激光超声检测系统：无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域，无损检测（NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统，以非接触式光学麦克风技术为核心，打破传统检测瓶颈，为半导体、航空航天、汽车制造等行业提供了高灵敏…...