数学建模——启发式算法(蚁群算法)
算法原理
蚁群算法来自于蚂蚁寻找食物过程中发现路径的行为。蚂蚁并没有视觉却可以寻找到食物,这得益于蚂蚁分泌的信息素,蚂蚁之间相互独立,彼此之间通过信息素进行交流, 从而实现群体行为。
蚁群算法的基本原理就是蚂蚁觅食的过程。首先,蚂蚁在觅食的过程中会在路径上留下信息素(pheromone),并在寻找食物的过程中感知这种物质的强度,并指导自己的行为方向,他们总会朝着浓度高的方向前进。因此可以看得出来,蚂蚁觅食的过程是一个正反馈的过程,该路段经过的蚂蚁越多,信息素留下的就越多,浓度越高,更多的蚂蚁都会选择这个路段。


运行实例

例题 (用蚁群算法解决旅行商问题)
假设有一个旅行商需要从城市1出发,经过若干个城市,最后回到城市1。已知城市之间的距离矩阵,旅行商的目标是最小化经过所有城市的总距离。请使用蚁群算法求解该问题。
-
问题定义:
- 假设有n个城市,城市之间的距离矩阵为D,其中D[i][j]表示城市i到城市j的距离。
-
初始化参数:
- 蚂蚁数量:m
- 信息素重要程度因子:alpha
- 启发函数重要程度因子:beta
- 信息素蒸发系数:rho
- 信息素增强系数:Q
- 最大迭代次数:iter_max
-
算法步骤:
- 初始化信息素矩阵tau,所有元素设为相同值。
- 迭代过程:
- 每只蚂蚁根据概率选择下一个城市,概率计算公式为:

- 更新路径和距离
- 更新信息素矩阵

- 重复迭代直到满足停止条件
- 每只蚂蚁根据概率选择下一个城市,概率计算公式为:
代码示例
import numpy as np
import random# 初始化参数
n = 10 # 城市数量
m = 50 # 蚂蚁数量
alpha = 1 # 信息素重要程度因子
beta = 5 # 启发函数重要程度因子
rho = 0.1 # 信息素蒸发系数
Q = 100 # 信息素增强系数
iter_max = 200 # 最大迭代次数# 生成距离矩阵
D = np.random.rand(n, n)
D = (D + D.T) / 2 # 确保距离矩阵是对称的
for i in range(n):D[i][i] = np.inf # 对角线元素设为无穷大# 初始化信息素矩阵
tau = np.ones((n, n))# 启发函数矩阵
eta = 1.0 / (D + np.eye(n))# 存储最佳路径
best_length = np.inf
best_path = []# 迭代过程
for iter in range(iter_max):# 存储每只蚂蚁的路径和距离paths = []lengths = []for i in range(m):path = []length = 0visited = np.zeros(n) # 标记已访问城市start = random.randint(0, n-1) # 随机选择起始城市visited[start] = 1path.append(start)for j in range(n-1):tabu = path # 禁忌表allow_list = [index for index in range(n) if index not in tabu] # 可访问城市列表P = np.zeros(len(allow_list)) # 计算概率# 计算转移概率for k in range(len(allow_list)):P[k] = np.power(tau[start][allow_list[k]], alpha) * np.power(eta[start][allow_list[k]], beta)P = P / P.sum()# 轮盘赌选择下一个城市next_city = allow_list[np.random.choice(range(len(allow_list)), p=P)]path.append(next_city)length += D[start][next_city]start = next_city# 回到起始城市length += D[start][path[0]]paths.append(path)lengths.append(length)# 更新最佳路径if length < best_length:best_length = lengthbest_path = path# 更新信息素矩阵delta_tau = np.zeros((n, n))for i in range(m):for j in range(n - 1):delta_tau[paths[i][j]][paths[i][j + 1]] += Q / lengths[i]delta_tau[paths[i][-1]][paths[i][0]] += Q / lengths[i]tau = (1 - rho) * tau + delta_tau# 输出结果print("最佳路径长度:", best_length)print("最佳路径:", best_path)
以上代码实现了基本的蚁群算法求解TSP问题。代码中,我们首先初始化了参数,并生成了城市之间的距离矩阵。然后,我们通过迭代过程让蚂蚁在每一轮中根据信息素和启发函数选择下一个城市,并记录每只蚂蚁的路径和路径长度。在每一轮迭代结束后,我们更新信息素矩阵,并记录下目前为止找到的最短路径。
需要注意的是,代码中的一些参数(如蚂蚁数量、信息素蒸发系数等)可以根据实际情况进行调整以获得更好的性能。此外,由于使用了随机数生成器,每次运行代码得到的结果可能有所不同。
最后,代码输出了最佳路径长度和路径。这只是一个简单的例子,蚁群算法可以应用于更复杂的问题,并且可以通过各种方式改进算法的性能。
结果展示

相关文章:

数学建模——启发式算法(蚁群算法)
算法原理 蚁群算法来自于蚂蚁寻找食物过程中发现路径的行为。蚂蚁并没有视觉却可以寻找到食物,这得益于蚂蚁分泌的信息素,蚂蚁之间相互独立,彼此之间通过信息素进行交流, 从而实现群体行为。 蚁群算法的基本原理就是蚂蚁觅食的过程…...
详解)
【Pytorch实用教程】在做模型融合时非常关键的代码:nn.Identity()详解
文章目录 nn.Identity()基础介绍主要用途示例代码以ResNet为例介绍 self.resnet.fc = nn.Identity() 的作用1. **背景:ResNet 模型结构**2. **代码 `self.resnet.fc = nn.Identity()` 的作用**3. **为什么使用 `nn.Identity()`**4. **示例代码**nn.Identity()基础介绍 nn.Ide…...

【开源力荐】一款基于web的可视化视频剪辑工具
嗨, 大家好, 我是徐小夕. 之前一直在社区分享零代码&低代码的技术实践,也陆陆续续设计并开发了多款可视化搭建产品,比如: H5-Dooring(页面可视化搭建平台)V6.Dooring(可视化大屏搭建平台)橙…...

鸿萌数据恢复服务: 如何修复 SQL Server 数据库错误 829?
天津鸿萌科贸发展有限公司从事数据安全服务二十余年,致力于为各领域客户提供专业的数据恢复、数据备份、网络及终端数据安全等解决方案与服务。 同时,鸿萌是众多国际主流数据恢复软件(Stellar、UFS、R-Studio、ReclaiMe Pro 等)的授权代理商,…...

OpenCV图像处理——按最小外接矩形剪切图像
引言 在图像处理过程中,提取感兴趣区域(ROI)并在其上进行处理后,往往需要将处理后的结果映射回原图像。这一步通常涉及以下几个步骤: 找到最小外接矩形:使用 cv::boundingRect 或 cv::minAreaRect 提取感兴…...

《熬夜整理》保姆级系列教程-玩转Wireshark抓包神器教程(4)-再识Wireshark
1.简介 按照以前的讲解和分享路数,宏哥今天就应该从外观上来讲解WireShark的界面功能了。 2.软件界面 由上到下依次是标题栏、主菜单栏、主菜单工具栏、显示过滤文本框、打开区、最近捕获并保存的文件、捕获区、捕获过滤文本框、本机所有网络接口、学习区及用户指…...

调用yolov3模型进行目标检测
要调用已经训练好的YOLOv3模型对图片进行检测,需要完成以下几个步骤: 加载预训练模型:从预训练的权重文件中加载模型。准备输入图片:将图片转换为模型所需的格式。进行推理:使用模型对图片进行推理,得到检…...

linux文件——重定向原理——dup、重定向与execl、VFS
前言:本篇讲解linux下的重定向相关内容。 在本篇中, 博主将会带着友友们一边实验, 一边探索底层原理。 通过本篇的学习, 友友们将会了解到重定向是如何实现的, 重定向的本质是什么, 重定向和进程替换之间的…...
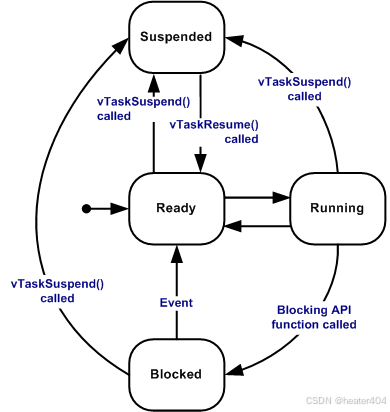
【STM32 FreeRTOS】任务
使用 RTOS 的实时应用程序可以被构建为一组独立的任务。每个任务在自己的上下文中执行,不依赖于系统内的其他任务或 RTOS 调度器本身。在任何时间点,应用程序中只能执行一个任务,实时 RTOS 调度器负责决定所要执行的任务。因此, R…...
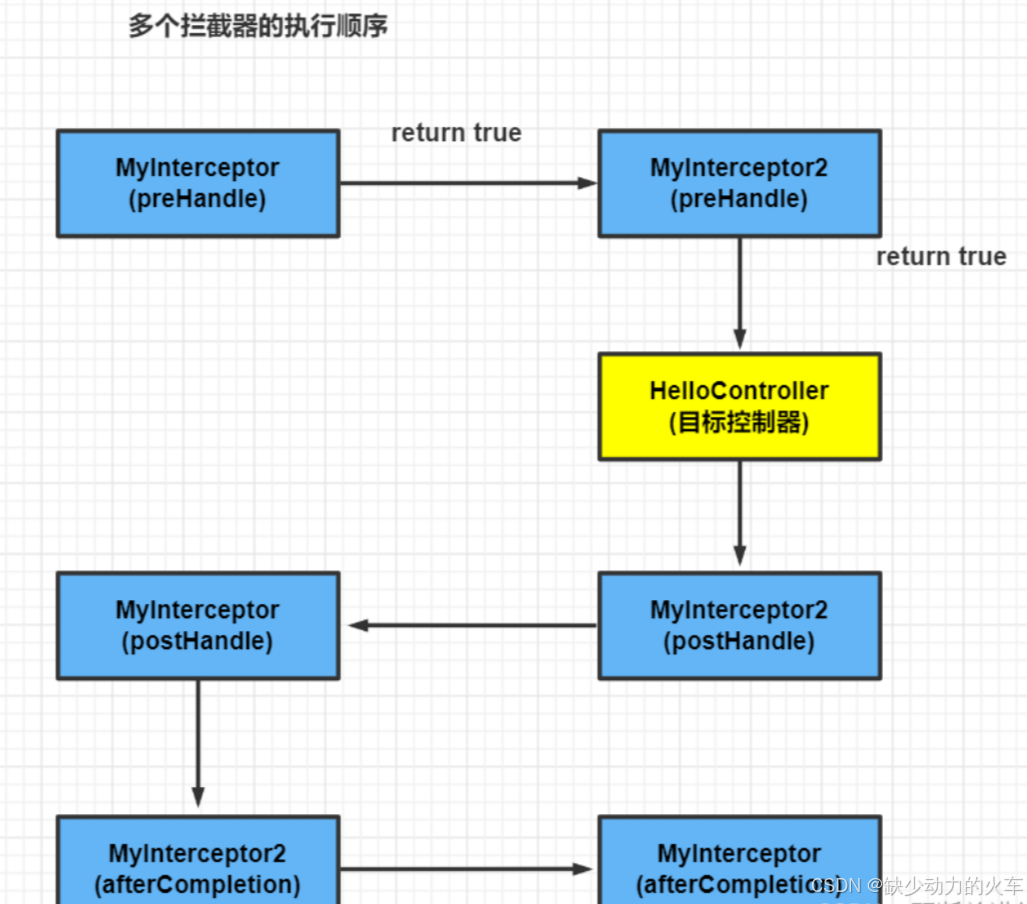
Java面试--框架--Spring MVC
Spring MVC 目录 Spring MVC1.spring mvc简介2.spring mvc实现原理2.1核心组件2.2工作流程 3.RESTful 风格4.Cookie,Session4.1 会话4.2 保存会话的两种技术 5.拦截器5.1过滤器、监听器、拦截器的对比5.2 过滤器的实现5.3 拦截器基本概念5.4 拦截器的实现 1.spring …...

土壤水分监测系统的工作原理
TH-TS200土壤水分监测系统是一种在地球科学、农学等领域广泛应用的分析仪器,它主要用于监测土壤中的水分含量,为农业生产、水资源管理、环境保护等提供重要数据支持。通常包括数据采集器、土壤水分传感器、土壤温度传感器(部分系统配备)、计算机软件以及…...

k8s学习--如何控制pod调度的位置
文章目录 一、Pod 调度基础二、通过节点选择器 (Node Selector) 控制调度三、使用节点亲和性 (Node Affinity)四、使用污点和容忍 (Taints and Tolerations)五、Pod 反亲和性 (Pod Anti-Affinity) 总结 在 Kubernetes (K8s)中,Pod 是应用运行的最小单位࿰…...
)
基于mysqldump的MySQL数据库异地备份方案(含完整脚本和解释)
MySQL数据库异地备份方案 0 文档描述 本文描述了一个数据库异地备份方案,以下脚本代码都是在线上应用的本文以CentOS7为例,其他系统请自行查询安装命令如果评论有需求,我就对应系统做一下文档 1 基本原理 1.1 流程 原理本身很简单&#…...

C语言中10个字符串函数详解
目录 1.strlen 2.strcpy 3.strcat 4.strcmp 5.strncpy 6.strncat 7.strncmp 8.strstr 9.strtok 10.strerror 1.strlen 基本结构:size_t strlen(const char *str);功能:用于计算字符串的长度;字符串已经 0作为结束标志…...

flume系列之:查询多个flume agent组是否有topic重复接入情况
flume系列之:查询多个flume agent组是否有topic重复接入情况 一、查询zk节点下的flume agent组二、获取采集的topic三、获取重复接入的topic,支持设置重复接入白名单四、执行流程五、完整代码一、查询zk节点下的flume agent组 def get_flumeAgent_zkPath(zkRootPaths):for z…...

Windows自动化1️⃣环境搭建WinAppDriver
对于技术选型: 我尝试了, pywinauto, WinAppDriver,CukeTest 担心CukeTest可能会收费, 尝试pywinauto,在元素点击,搜索时, 遇到不可用情况; WinAppDriver是微软家的,大厂开源, 就它了! 步骤一:安装WinAppDriver 进入WinAppDriver下载页面(https://githu…...

云服务器Docker内部署服务后,端口无法访问?
云服务器Docker内部署服务后,端口无法访问,可以按照以下思路进行排查: 以【docker run --name my-nginx -d -p 9395:80 nginx】举例: 查看Docker映射是否正确,可使用docker ps命令查看。Docker是否设置端口映射&#…...

Unity将摄像机视角保存成Json文件方便读取使用
系列文章目录 unity工具 文章目录 系列文章目录👉前言👉一、设置环境👉二、代码如下👉三、使用方法 👉四、下次外部调用json里面的摄像机位置的时候如下代码方法👉壁纸分享👉总结 👉…...
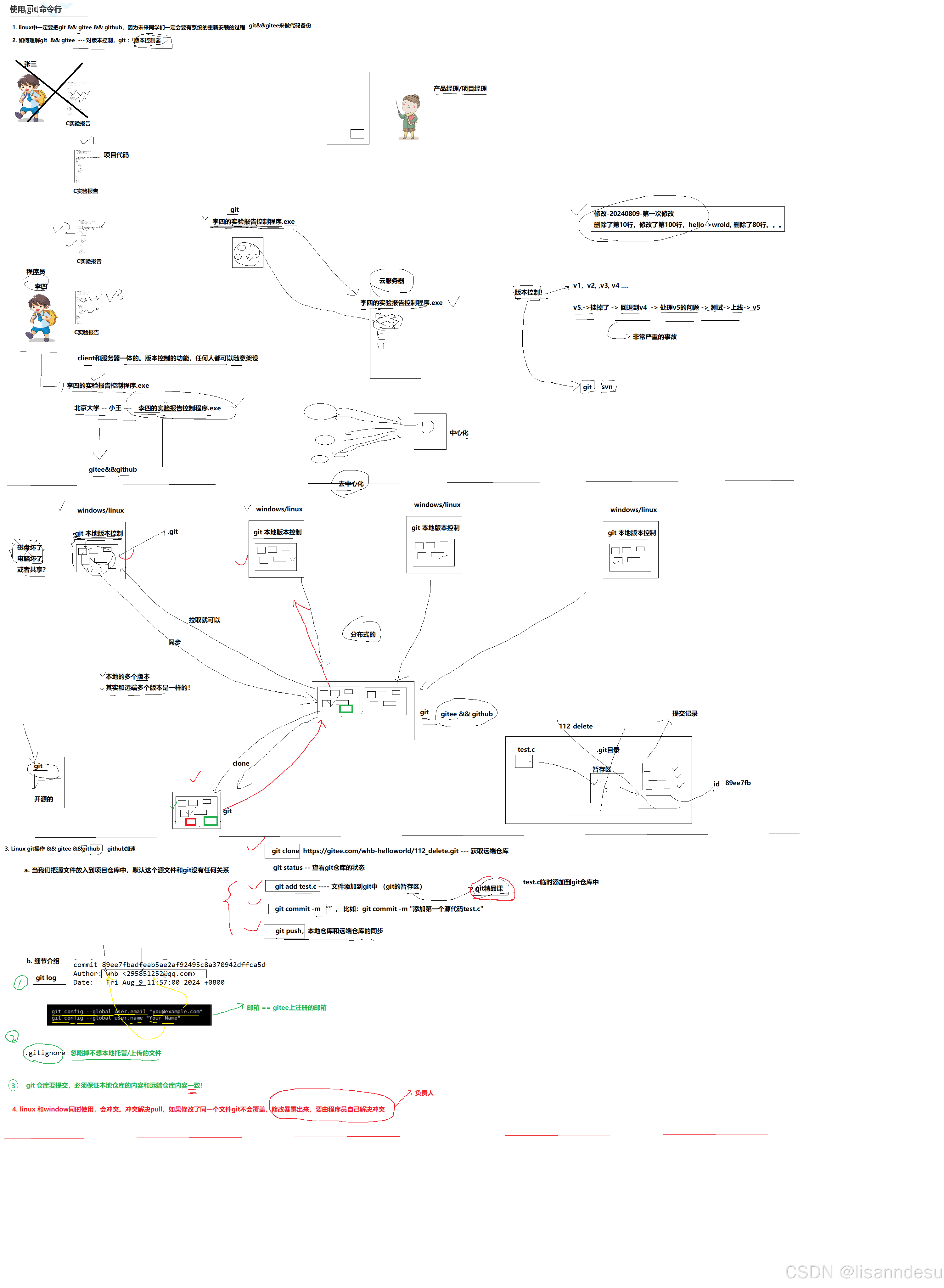
git是什么/基本指令
git作用 去中心化, 分布式版本控制器 新增术语:仓库区, 工作区, 暂存区 具体见下板书 常用git命令 git clone 仓库网址 git status 查看仓库状态 git add newfile 临时添加到git仓库 git commit -m 正式添加git仓库 g…...
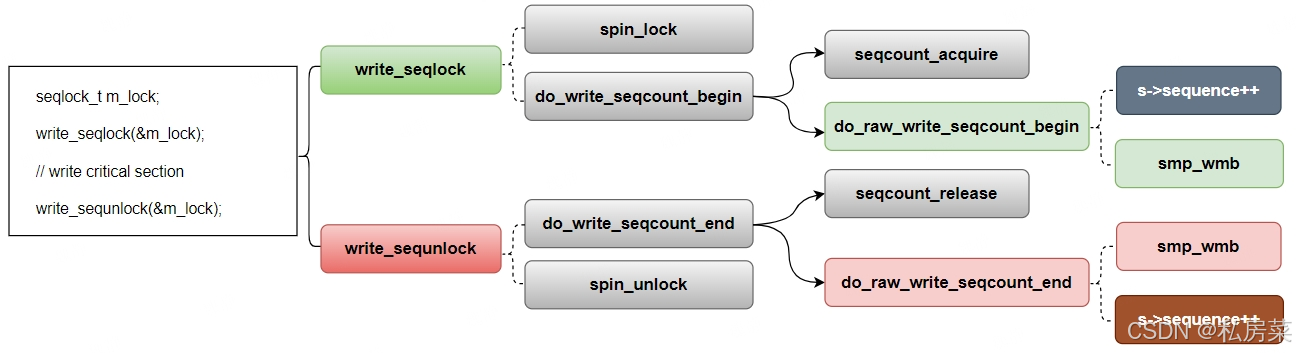
Linux 中的同步机制
代码基于:Kernel 6.6 临界资源:指哪些在同一时刻只允许被一个线程访问的软件或硬件资源。这种资源的特点是,如果有线程正在使用,其他进程必须等待直到该线程释放资源。 临界区:指在每个线程中访问临界资源的那段代码。…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
