二叉树详解(1)
文章目录
- 目录
- 1. 树的概念及结构
- 1.1 树的相关概念
- 1.2 树的表示
- 1.3 树在实际中的运用(表示文件系统的目录树结构)
- 2. 二叉树的概念及结构
- 2.1 概念
- 2.2 特殊的二叉树
- 2.3 二叉树的存储结构
- 3. 二叉树的顺序结构及实现
- 3.1 二叉树的顺序结构
- 3.2 堆的概念及结构
- 3.3 堆的实现
- 3.4 堆的应用
- 3.4.1 堆排序
- 3.4.2 TOP-K问题
目录
- 树的概念及结构
- 二叉树的概念及结构
- 二叉树的顺序结构及实现
- 二叉树链式结构的实现
1. 树的概念及结构
1.1 树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点(没有孩子的节点)
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点(亲兄弟)
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
注:数组的下标从零开始是因为要和指针更好的匹配:a[i] = *(a + i);而在这里我们更习惯把根定义为第一层,当然,定义成第零层也是可以的
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林(并查集)
注: 现在我们看到树就要把它进行拆分成:根和n棵子树(n>=0);树是按照递归定义的,也就是说子树也要按照这个方式进行拆分。

也就是说树是不能有环的,有环的就称为图。
通过以上学习,我们总结一下树的概念:树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点。
- 除根节点外,其余结点被分成 M(M>0) 个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
- 因此,树是递归定义的。
1.2 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既要保存值域,也要保存结点和结点之间的关系。
//树的度是N#define N 6struct TreeNode
{int val;struct TreeNode* subA[N];
};
但是这样定义太浪费空间了,因为并不是每个节点的度都达到了N。
因此,我们可以借助顺序表来解决这个问题:
struct TreeNode
{int val;//顺序表struct TreeNode** subA;int size;int capacity;
};
但这种表示也不是最常见的,接下来我们介绍一种新的定义方式:
//左孩子 右兄弟
struct TreeNode
{int val;struct TreeNode* leftChild;struct TreeNode* nextBrother;
};
第一个指针永远指向从左往右数的第一个孩子,第二个指针指向它自己右边的亲兄弟。
那么一个父亲如何找到他所有的孩子呢?

其实还有一种表示方式,这里我们先了解一下就可以:

用数组存储数据,数组的每个元素都是一个结构体,每个结构体包含节点的值和父亲所在的下标;这种表示法可以用来表示森林。
它的物理结构:数组(内存中如何存储)
逻辑结构:森林(想象出来的)
1.3 树在实际中的运用(表示文件系统的目录树结构)
数据结构分为表示形和存储形,树这种数据结构就属于表示形,主要是用来表示某种结构。

在Windows系统中也是一样的,比如C盘作为根,里面包含了很多文件夹,每个文件夹中又包含了很多文件夹,它们的底层就是通过树这种数据结构来实现的。
2. 二叉树的概念及结构
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注: 对于任意的二叉树都是由以下几种情况复合而成的:

二叉树单纯存储数据是没啥价值,不如顺序表/链表,那我们为什么要学二叉树呢?

但是它也存在不足,在极端情况下可能会变成这样:

因此,我们后面还要学AVL树和红黑树;同时还会有多叉树:M阶B树,多用于数据库的引擎
2.2 特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树;也就是说,如果一个二叉树的层数为K,且结点总数是 2的k次方 - 1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树,要注意的是满二叉树是一种特殊的完全二叉树。

简单来说: 满二叉树就是前 n - 1 层都是满(度为2),最后一层是叶子结点;完全二叉树就是前 n - 1 层都是满,最后一层不一定满,但要求从左到右的节点是连续的。
2.3 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
-
顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

-
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面我们学到高阶数据结构如红黑树等会用到三叉链。

3. 二叉树的顺序结构及实现
3.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费;而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2 堆的概念及结构

3.3 堆的实现
我们先以小堆为例(大堆就是 ‘<’ 改成 ‘>’):
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
堆的插入:

void Swap(HPDataType* px, HPDataType* py)
{HPDataType* tmp = *px;*px = *py;*py = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)//这样写是不对的,parent永远都是 >= 0 的while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){size_t newCapacity = 0 == php->capacity ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (NULL == tmp){perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}
堆的删除:


void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//假设法,选出左右孩子中小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}
完整代码:
//Heap.h#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HPInit(HP* php);
void HPDestroy(HP* php);//插入后保持数据是堆
void HPPush(HP* php, HPDataType x);HPDataType HPTop(HP* php);//删除堆顶的数据
void HPPop(HP* php);bool HPEmpty(HP* php);
//Heap.c#include "Heap.h"void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = 0;php->size = 0;
}void Swap(HPDataType* px, HPDataType* py)
{HPDataType* tmp = *px;*px = *py;*py = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)//这样写是不对的,parent永远都是 >= 0 的while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}//时间复杂度:logN
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){size_t newCapacity = 0 == php->capacity ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (NULL == tmp){perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//假设法,选出左右孩子中小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//时间复杂度:logN
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}bool HPEmpty(HP* php)
{assert(php);return 0 == php->size;
}
//Test.c#include "Heap.h"int main()
{//如何把以下数组变成一个堆//int a[] = { 50, 100, 70, 65, 60, 32 };int a[] = { 60, 70, 65, 50, 32, 100 };HP hp;HPInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&hp, a[i]);}//printf("%d\n", HPTop(&hp));//HPPop(&hp);//printf("%d\n", HPTop(&hp));while (!HPEmpty(&hp)){printf("%d\n", HPTop(&hp));HPPop(&hp);}HPDestroy(&hp);return 0;
}
堆插入和删除的时间复杂度:

如果一开始就给了一个数组,如何给它初始化成堆呢?
- 模拟插入,向上调整建堆
void HPInitArray(HP* php, HPDataType* a, int n)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (NULL == php->a){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HPDataType) * n);php->capacity = php->size = n;//向上调整,建堆 O(N*logN)for (int i = 1; i < php->size; i++){AdjustUp(php->a, i);}
}
时间复杂度:

总结: 节点数量越多的时候,调整次数也越多
- 向下调整建堆
向下调整建堆的前提是它的左右子树都已经是大/小堆了,所有不能从第一个节点开始向下调整,而是从最后一个节点开始向下调整,但是最后一层是叶子节点,不需要调整就已经是堆了,所有就从倒数第一个非叶子节点开始向下调整。

void HPInitArray(HP* php, HPDataType* a, int n)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (NULL == php->a){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HPDataType) * n);php->capacity = php->size = n;//向下调整,建堆 O(N)for (int i = (php->size - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, php->size, i);}
}
时间复杂度:

总结: 节点数量多的时候,调整次数少
因此,直接给一个数组让它建堆比一个一个插入,向上调整建堆效率要高。
int main()
{//如何把以下数组变成一个堆//int a[] = { 50, 100, 70, 65, 60, 32 };int a[] = { 60, 70, 65, 50, 32, 100 };HP hp;HPInitArray(&hp, a, sizeof(a) / sizeof(int));while (!HPEmpty(&hp)){printf("%d\n", HPTop(&hp));HPPop(&hp);}HPDestroy(&hp);return 0;
}
3.4 堆的应用
3.4.1 堆排序
根据我们上面所讲的,我们可以很容易想到这种写法:
void HeapSort(int* a, int n)
{HP hp;HPInitArray(&hp, a, n);int i = 0;while (!HPEmpty(&hp)){a[i++] = HPTop(&hp);HPPop(&hp);}HPDestroy(&hp);
}int main()
{int a[] = { 60, 70, 65, 50, 32, 100 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}
但是这样写有两个问题:
- 需要堆的数据结构
- 空间复杂度 O(N)
可以这样改进:

void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//假设法,选出左右孩子中小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//升序,建大堆还是小堆呢?大堆
//O(N * logN)
void HeapSort(int* a, int n)
{//a数组直接建堆 O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}//O(N * logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}int main()
{int a[] = { 3, 6, 1, 5, 8, 9, 2, 7, 4, 0 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}
之前在写堆的代码时,可能会存在这样的疑问:为什么向下调整函数的参数不传堆的结构体指针,而是只传数组的地址进去呢?
这里就体现出来了:因为这个函数在堆排序的时候还需要用到,如果传了堆的结构体指针,那这里就不好复用了。(这个函数不仅仅用来服务堆这个数据结构,还需要服务于堆排序)
3.4.2 TOP-K问题
100亿个数据,找出最大的前10个(N个数据里面找最大的前K个,N远大于K)
注: 如果N和K差不多大,可以直接排序解决
最容易想到的方法就是把这100亿个数据建一个大堆,每次找出最大的,然后将它删掉,再找次大的,一直循环10次。
但是这种方法存在问题:
- 时间复杂度:N + K * logN
- 最主要的问题是空间复杂度,堆底层就是个数组,它开不出这么大的一个数组,内存空间不够
因此,我们就要换一种方法:

void CreateNDate()
{//造数据int n = 100000;srand((unsigned int)time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (NULL == fin){perror("fopen error");return;}for (int i = 0; i < n; ++i){//随机数系统规定只有三万多个//+i 是为了让数据的随机性更大一点//%1000000 是为了让数据在1000000以内,这样我们可以手动让几个数据大于1000000,以此来验证我们程序的正确性int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void topk()
{printf("请输入k:>");int k = 0;scanf("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (NULL == fout){perror("fopen error");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (NULL == minheap){perror("malloc error");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}//建k个数据的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(minheap, k, i);}int x = 0;while (fscanf(fout, "%d", &x) != EOF){//读取剩余数据,比堆顶的值大,就替换它进堆if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}fclose(fout);free(minheap);minheap = NULL;
}int main()
{CreateNDate();topk();return 0;
}
相关文章:

二叉树详解(1)
文章目录 目录1. 树的概念及结构1.1 树的相关概念1.2 树的表示1.3 树在实际中的运用(表示文件系统的目录树结构) 2. 二叉树的概念及结构2.1 概念2.2 特殊的二叉树2.3 二叉树的存储结构 3. 二叉树的顺序结构及实现3.1 二叉树的顺序结构3.2 堆的概念及结构…...

Spring定时任务注解
Service EnableScheduling public class xxxServiceImpl implement xxxService{Scheduled(cron "0 15 11 * * ?") // 每天的11:15执行public void reportCurrentTime() {aaa();}Scheduled(cron "0 15 17 * * ?") // 每天的17:15执行public void report…...

数据结构-绪论
学习目标: 认识数据结构的基本内容 学习内容: 了解:数据结构的研究内容掌握:数据结构的基本概念和术语了解:数据元素间的结构关系掌握:算法及算法的描述 数据结构的发展: 数据结构的发展简史 …...

Web开发:web服务器-Nginx的基础介绍(含AI文稿)
目录 一、Nginx的功能: 二、正向代理和反向代理的区别 三、Nginx负载均衡的主要功能 四、nginx安装目录下的各个文件(夹)的作用: 五、常用命令 一、Nginx的功能: 1.反向代理:例如我有三台服务器&#x…...

共享经济背景下校园、办公闲置物品交易平台-计算机毕设Java|springboot实战项目
🍊作者:计算机毕设残哥 🍊简介:毕业后就一直专业从事计算机软件程序开发,至今也有8年工作经验。擅长Java、Python、微信小程序、安卓、大数据、PHP、.NET|C#、Golang等。 擅长:按照需求定制化开发项目、 源…...

Linux 服务器上简单配置 minio
Linux 服务器上简单配置 minio 初始化结构目录 mkdir -p /data/minio/bin mkdir -p /data/minio/conf mkdir -p /data/minio/data 下载 minio cd /data/minio/bin curl -O https://dl.min.io/server/minio/release/linux-amd64/minio 添加执行权限 chmod x minio 创建配置文件…...

TypeScript 面试题汇总
引言 TypeScript 是一种由微软开发的开源、跨平台的编程语言,它是 JavaScript 的超集,为 JavaScript 添加了静态类型系统和其他高级功能。随着 TypeScript 在前端开发领域的广泛应用,掌握 TypeScript 已经成为很多开发者必备的技能之一。本文…...

杰卡德系数
杰卡德系数(Jaccard Index 或 Jaccard Similarity Coefficient) 杰卡德系数是一种用于衡量两个集合相似度的重要指标。 从数学定义上来看,如前面所述,杰卡德系数计算公式为: J ( A , B ) ∣ A ∩ B ∣ ∣ A ∪ B ∣…...

微服务实现-sleuth+zipkin分布式链路追踪和nacos配置中心
1. sleuthzipkin分布式链路追踪 在大型系统的微服务化构建中,一个系统被拆分成了许多微服务。这些模块负责不同的功能,组合成系统,最终可以提供丰富的功能。 这种架构中,一次请求往往需要涉及到多个服务。互联网应用构建在不同的软…...

数学中常用的解题方法
文章目录 待定系数法应用示例1. 多项式除法2. 分式化简3. 数列通项公式 总结 递归数列特征方程特征根的求解通项公式的求解示例 错位相减,差分错位相减法差分的应用结合理解 韦达定理二项式定理二项式定理的通项公式二项式系数的性质应用示例 一元二次求解1. 因式分…...

pytorch 1 张量
张量 文章目录 张量torch.Tensor 的 主要属性torch.Tensor 的 其他常用属性和方法叶子张量(Leaf Tensors)定义叶子张量的约定深入理解示例代码总结 中间计算结果与 detach() 方法定义中间计算结果不是叶子节点使用 detach() 方法使中间结果成为叶子张量示…...

音视频开发继续学习
RGA模块 RGA模块定义 RGA模块是RV1126用于2D图像的裁剪、缩放、旋转、镜像、图片叠加等格式转换的模块。比方说:要把一个原分辨率1920 * 1080的视频压缩成1280 * 720的视频,此时就要用到RGA模块了。 RGA模块结构体定义 RGA区域属性结构体 imgType&am…...

【Datawhale X 魔搭 】AI夏令营第四期大模型方向,Task1:智能编程助手(持续更新)
在一个数据驱动的世界里,人工智能的未来应由每一个愿意学习和探索的人共同塑造和掌握。希望这里是你实现AI梦想的起点。 大模型小白入门:https://linklearner.com/activity/14/11/25 大模型开发工程师能力测试:https://linklearner.com/activ…...
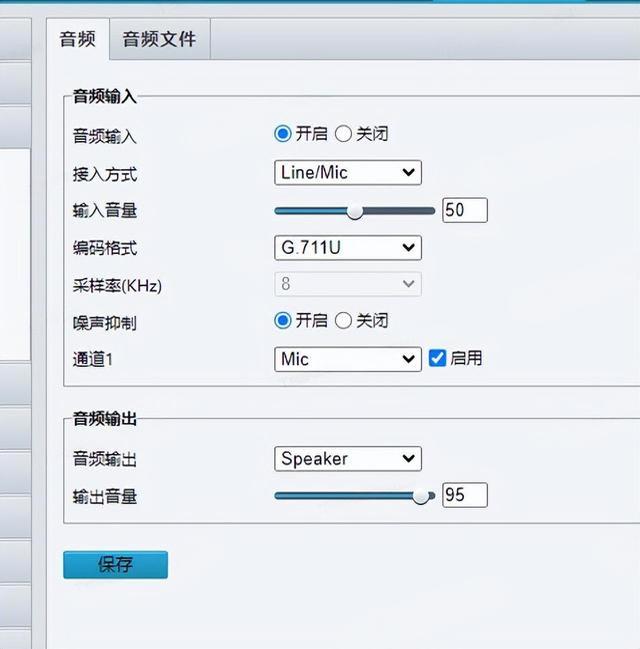
如何判断监控设备是否支持语音对讲
目录 一、大华摄像机 二、海康摄像机 三、宇视摄像机 一、大华摄像机 注意:大华摄像机支持跨网语音对讲,即设备和服务器可以不在同一网络内,大华设备的语音通道填写:34020000001370000001 配置接入示例: 音频输入…...
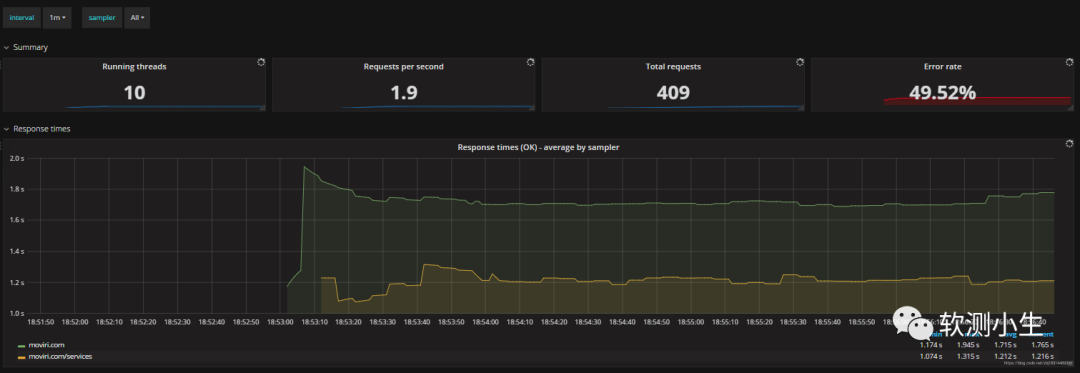
Grafana+Influxdb(Prometheus)+Apache Jmeter搭建可视化性能测试监控平台
此性能测试监控平台,架构可以是: GrafanaInfluxdbJmeterGrafanaPrometheusJmeter Influxdb和Prometheus在这里都是时序性数据库 在测试环境中,压测数据对存储和持久化的要求不高,所以这里的组件可以都通过docker-compose.yml文件…...

【笔记】MSPM0G3507移植RT-Thread——MSPM0G3507与RT_Thread(二)
一.创建新工程 找到"driverlib\empty"空白工程,CTRLC然后CTRLV复制副本 重命名为G3507_RTT 打开KEIL工程 双击empty.syscfg,然后打开SYSCONFIG 我的不知道为啥没有48pin选项,如果你也一样,可以跟着我做,如果…...

计算机毕业设计 美发管理系统 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

soapui调用接口参数传递嵌套xml,多层CDATA表达形式验证
1.环境信息 开发工具:idea 接口测试工具:soapui 编程语言:java 项目环境:jdk1.8 webservice:jdk自带的jws 处理xml:jdk自带的jaxb 2.涉及代码 package org.example.webdemo;import javax.jws.WebMethod; i…...

GB/T35561-2017d,GB/T38565-2020,ocr解析文本
因系统需要只找到pdf版本,解析一版记录 GB/T35561-2017d 10000 , 自然灾害 10100 , 水旱灾害 10101 , 洪水 10102 , 内涝 10103 , 水库重大险情 10104 , 堤防重大险情 10105 , 凌汛 10106 , 山洪 10107 , 农业干旱 10108 , 城镇缺水 10109 , 生态干旱 10110 , 农村…...

IDEA使用LiveTemplate快速生成方法注释
本文目标:开发人员,在了解利用Live Template动态获取方法输入输出参数、创建日期时间方法的条件下,进行自动生成方法注释,达到自动添加方法注释的程度; 文章目录 1 场景2 要点2.1 新增LiveTemplate模版2.2 模版内容填写…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...
