直面风口,未来不仅是中文版ChatGPT,还有AGI大时代在等着我们
说到标题的AI2.0这个概念的研究早在2015年就研究起步了,其实大家早已知道,人工智能技术必然是未来科技发展战略中的重要一环,今天我们就从AI2.0入手,以GPT-4及文心一言的发布为切入角度,来谈一谈即将降临的AGI时代。
关于AI
关于AI,早在1956年,达特茅斯就提出了“人工智能”这个概念。当时有一批著名学者,包括斯坦福的McCrarthy教授、MIT的Minsky教授,卡内基·梅隆的Simont和Newell教授(以上四位后来都成为图灵奖获得者),还有贝尔实验室的Shannon、IBM公司的Rochester等。当时他们便确立了“人工智能”的概念:让机器能像人那样认知、思考和学习,即用计算机模拟人的智慧。

随后在70年代,人工智能研究学界主要瞄准了七个方向,这七个方向一直到现在都发挥着很重要的作用。包括
机器定理证明,现在是逻辑和推理;机器翻译,现在是自然语言处理;专家系统,现在是问题求解和知识表达;博弈,现在是树搜索;模式识别,现在是多媒体认知;学习,现在是神经网络;机器人和智能控制,现在是感知和控制。
在当时,AI2.0是基于重大变化的信息新环境和发展新目标的新一代人工智能。而其中,信息新环境是指:互联网与移动终端的普及、传感网的渗透、大数据的涌现和网上社区的兴起等等。新目标是指:智能城市、智能经济、智能制造、智能医疗、智能家居、智能驾驶等从宏观到微观的智能化新需求。
热火朝天
咱这圈里今年可是数次都火出了圈,从全民跟风的ChatGPT到现在的文心一言,今年放在人工智能技术上的镜头格外得多。那么在此等技术发展的背景下,现阶段的AI2.0又指的是啥呢?
我们要清楚地认识到,现阶段的AI2.0的范式具有三个特点:第一,无需人工标注。可以阅读海量的文本,进行自监督学习;第二,模型规模大。需要几千张 GPU 来训练,消耗巨大的数据量和资金量;第三,拥有跨领域能力。可以通过微调(fine-tuning)以较低的成本训练,以适应不同领域的任务,从文本延伸到其他。

而作为AI 2.0时代的第一个现象级应用——生成式 AI(Generative AI),也就是国内从去年来一直被热议的AIGC。它能够实现无需标注的自监督学习,自此AI 将从“辅助”人到逐步“替代”人工,所有使用者界面将被重新设计改写。
展开角逐
正如李开复先生所说的:“AI 2.0 时代的来临,是巨大的平台式机会,而且这将是中国在AI领域的第一次参与平台角逐的机会。”
就目前来看,OpenAI发布了GPT-4,但百度推出的文心一言截至目前来看也算是顶住了GPT-4的压力,这在我们的人工智能技术也是一个好消息,我们也并非止步于此,国内各企业也在技术层面上,奋起直追。

新一代信息技术与人工智能技术的飞速发展,意味着社会进入万物智联时代,在数字化基础上,“数智化”形成了更高的转型发展诉求。云计算、大数据、人工智能等技术的发展,也推动企业的数字化建设向数智融合方向转型,各企业的数智化进程该提速了!低代码开发平台为企业带来了更多降本增效的解决方案,涌现出引迈信息等一批致力于助力企业数智化转型的企业。
JNPF快速开发平台作为引迈旗下的王牌,其业务覆盖金融、政府、制造、教育、医疗、建筑、交通等多个领域,致力于帮助合作企业快速完成项目的研发与交付。
通过在线开发、流程引擎、代码生成等核心功能快速构建相关业务系统,可以帮助开发者实现5分钟配置一张业务表单、5小时搭建一个专属应用、5天落地一个管理方案,并且易于维护、易于扩展、安全稳定,助力企业打通数智化的“最后一公里”,为企业数字化提供服务的软件解决方案。

除了有好用的开发工具帮助转型之外,企业也需采用更加长远专业的战略、更加精准施策的手段去实施数智化转型。JNPF将立足企业实际业务场景,在通用解决方案基础上满足企业的个性化需求。
相关文章:

直面风口,未来不仅是中文版ChatGPT,还有AGI大时代在等着我们
说到标题的AI2.0这个概念的研究早在2015年就研究起步了,其实大家早已知道,人工智能技术必然是未来科技发展战略中的重要一环,今天我们就从AI2.0入手,以GPT-4及文心一言的发布为切入角度,来谈一谈即将降临的AGI时代。 关…...
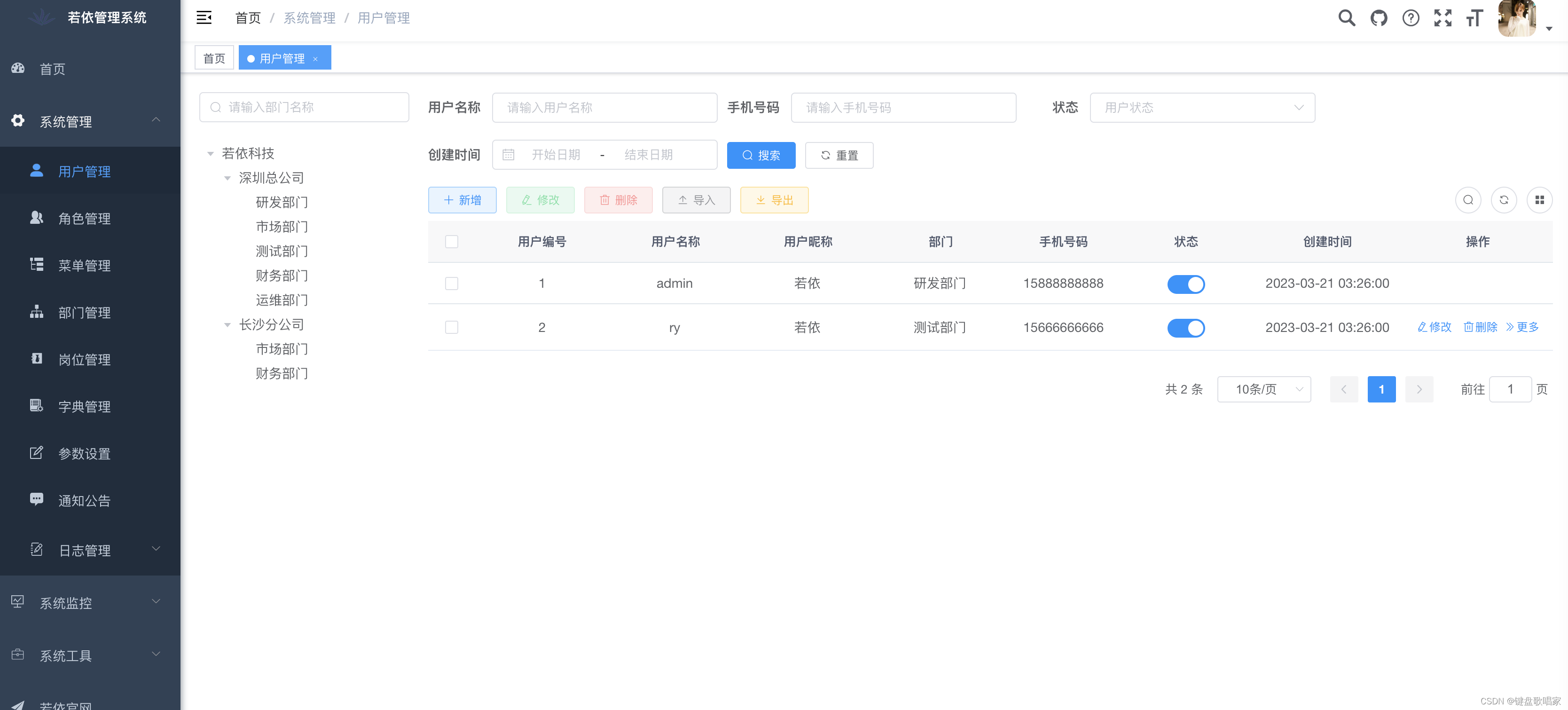
若依微服务(ruoyi-cloud)保姆版容器编排运行
一、简介 项目gitee地址:https://gitee.com/y_project/RuoYi-Cloud 由于该项目运行有很多坑,大家可以在git克隆拷贝到本地后,执行下面的命令使master版本回退到本篇博客的版本: git reset --hard 05ca78e82fb4e074760156359d09a…...
vue2图片预览插件
学习:vue插件开发实例-图片预览插件 vue2-pre-img-plugin的gitee代码 准备工作 准备图片与基础的样式 将iconfont下载的字体图标资源放在src/assets/iconfont目录下将准备预览的图片放到src/static/images目录下 PrevImg.vue 在plugins/PrevImg目录下ÿ…...

手写Promise源码的实现思路
Promise的使用: let promise new Promise((resolve, reject) > {resolve("OK");// reject("Error"); });console.log(promise);promise.then(value > {console.log("success"); }, error > {console.log("fail"…...

【数据结构】-关于树的概念和性质你了解多少??
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! 树前言一、树概念及结构1.1树的概念1.2 树的相关概念1.3 树的表示1.4树在实际中的运用…...

【前端之旅】NPM必知必会
一名软件工程专业学生的前端之旅,记录自己对三件套(HTML、CSS、JavaScript)、Jquery、Ajax、Axios、Bootstrap、Node.js、Vue、小程序开发(UniApp)以及各种UI组件库、前端框架的学习。 【前端之旅】Web基础与开发工具 【前端之旅】手把手教你安装VS Code并附上超实用插件…...

Android SQLite使用事务来确保所有语句都以原子方式执行及保证数据完整性一次执行多条语句示例
execSQL 不支持用分号分隔一次执行多个 SQL 语句,虽然理论上可以实现。但是,并不建议这样做,因为这可能会导致潜在的 SQL 注入漏洞。相反,建议使用 execSQL 或 rawQuery 分别执行每个语句。 在下面的代码块中,我们正在…...
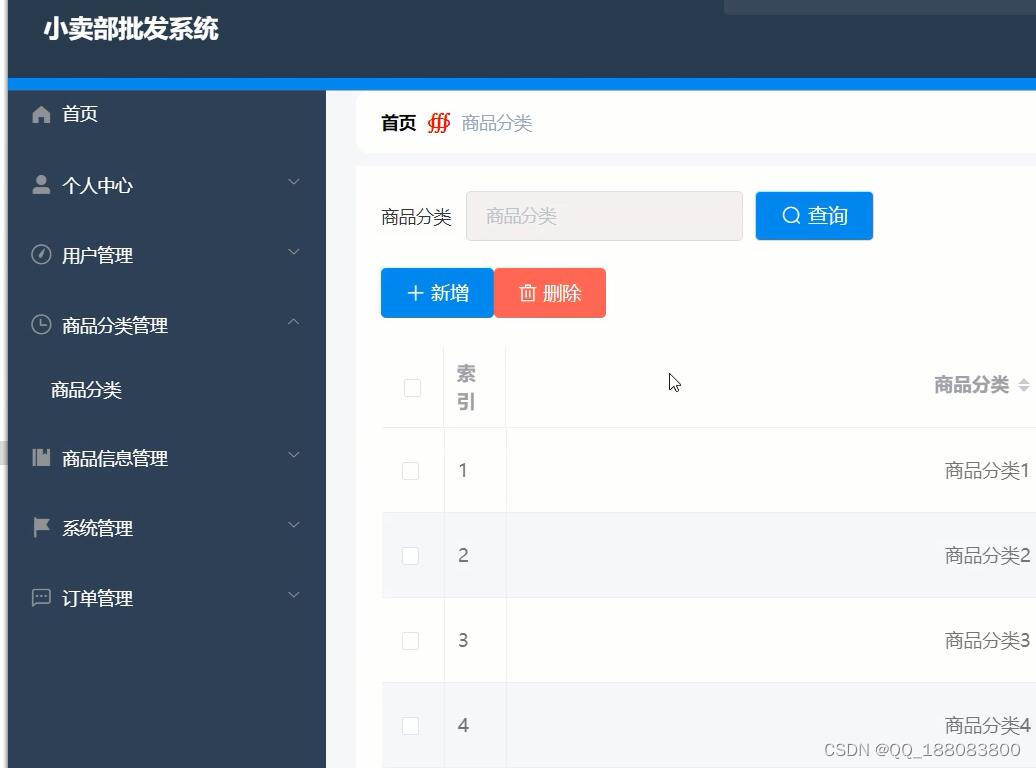
nodejs+vue校园超市小卖部零食在线购物商城系统
21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存储达到…...
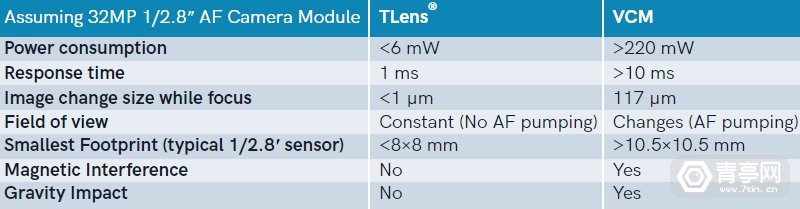
Karl Guttag:论相机对焦技术在AR/VR中的沿用
近期,AR/VR光学专家Karl Guttag介绍了两家在CES 2023展出光学传感技术的公司:poLight和CML(剑桥机电一体化)。同时介绍两家公司的原因,是因为他们提供了实现AR/VR“光学微动”(Optics Micromovement&…...
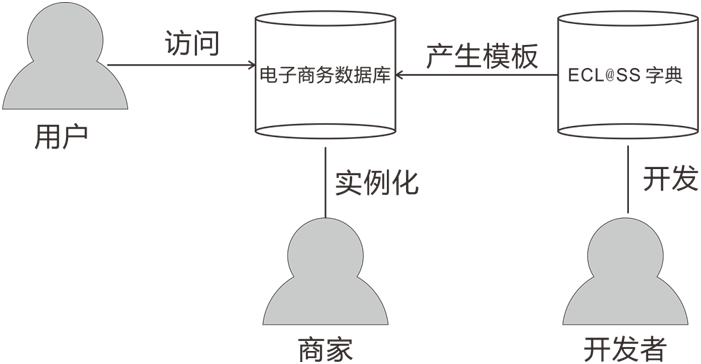
ECL@SS学习笔记(3)-概念数据模型
ECLSS 是产品,服务的分类和描述系统。本文介绍其内部的数据模型。ECLSS的作用ECLSS 标准的目标是为了实现工业界数据交换的标准化。这个标准主要作用是产品的分类和描述。分类为了有效地物料管理,供应链管理和电子商务,需要对物料进行分类和编…...

206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3: 输…...
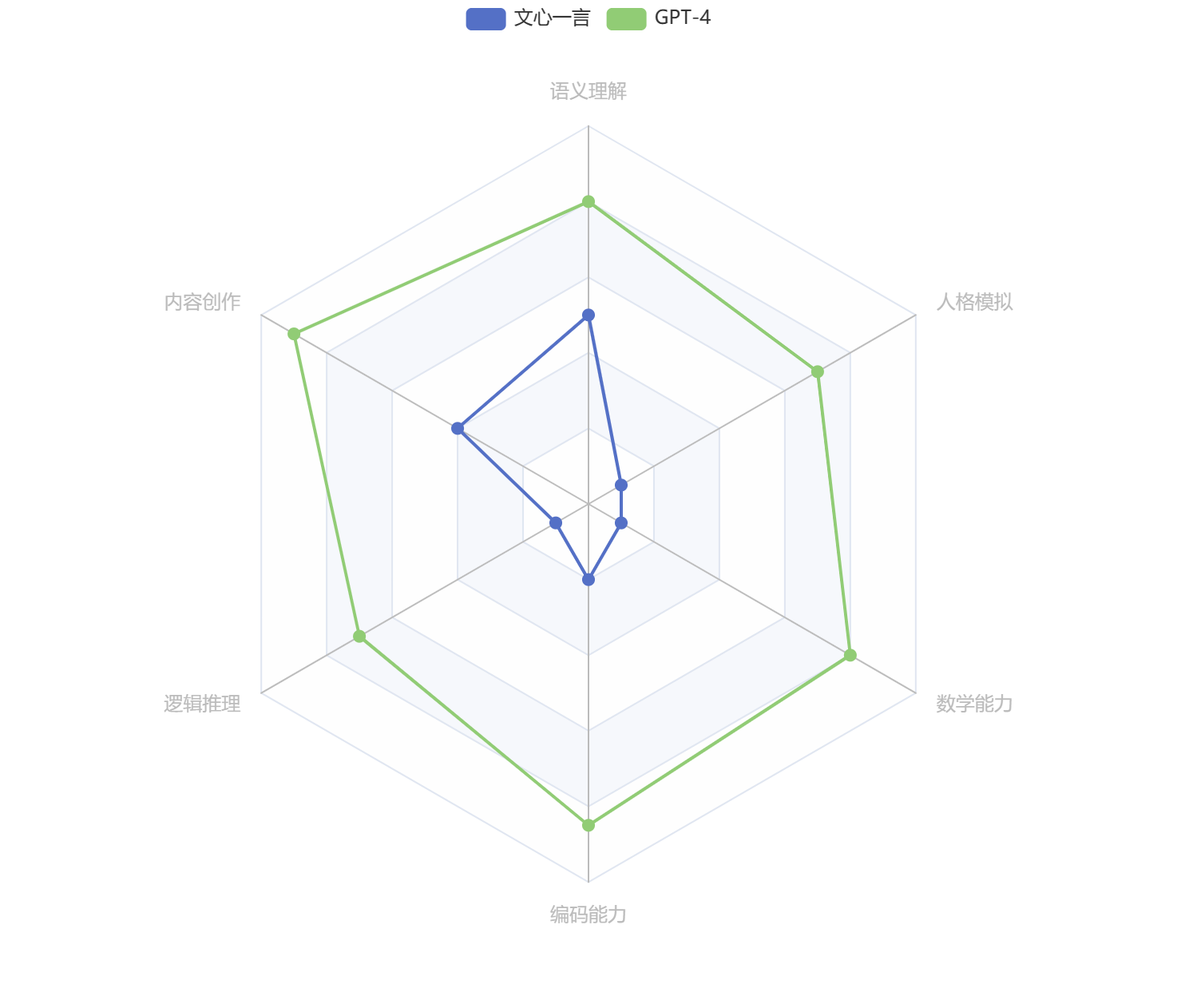
文心一言 vs GPT-4 —— 全面横向比较
文心一言 vs GPT-4 —— 全面横向比较 3月15日凌晨,OpenAI发布“迄今为止功能最强大的模型”——GPT-4。我第一时间为大家奉上了体验报告《OpenAI 发布GPT-4——全网抢先体验》。 时隔一日,3月16日下午百度发布大语言模型——文心一言。发布会上&#…...

rancher2.6进阶之kubectl安装
rancher2.6进阶之kubectl安装 1.安装kubectl客户端 1.1.1.使用命令行下载安装包: curl -LO https://dl.k8s.io/release/$(curl -L -s https://dl.k8s.io/release/stable.txt)/bin/linux/amd64/kubectl Note: 可指定下载版本, 将 ( c u r l − L − s h t t p s : / / d l . k …...

图像基本变换
缩放与裁剪裁剪图像的裁剪,是指将图像的某个区域切割出来。一些常见的应用场景包括:* 感兴趣区域提取* 去除无用信息* 图像增强* 纠偏:去除不规则部分,将图像变得更加整齐事实上,图像裁剪的裁剪通常就是一个numpy矩阵切…...
基于文心一言的底层视觉理解,百度网盘把「猫」换成了「黄色的猫」
随着移动互联网的一路狂飙,手机已经成为人们的新器官。出门不带钥匙可以,不带手机却是万万不可以的。而手机上,小小的摄像头也越来越成为各位「vlogger」的口袋魔方。每天有超过数亿的照片和视频被上传到百度网盘中,这些照片和视频…...

安卓开发的环境配置教程
文章目录事先准备:下载 JDK、Gradle下载安装 Android Studio下载安装 Android SDK下载安装 ADB笔者的环境: Java 17.0.1 Gradle 8.0.1 Android Studio Electric Eel | 2022.1.1 Patch 1 Windows 10 教育版 64位 事先准备:下载 JDK、Gradl…...

【Spring Cloud Alibaba】Spring Cloud Alibaba 搭建教程
文章目录教程适用版本一、简介主要功能组件开源地址二、开始搭建1.项目搭建与依赖管理2.服务注册与发现(Nacos安装)3.创建服务提供者4.创建服务消费者5.创建服务消费者(Feign)6.添加熔断机制(Sentinel)7.Sentinel熔断器仪表盘监控…...

关于自动机器学习flaml训练时的一些报错
一、版本背景flaml 1.1.3sciket-learn 0.23.0二、一路报错2.1、SyntaxError: future feature annotations is not definedTraceback (most recent call last):File "C:/Users/dell/Desktop/AI/run.py", line 151, in <module>model.autoMlArgs(queryDf,targe…...
是什么?)
【计算机视觉】消融实验(Ablation Study)是什么?
文章目录一、前言二、定义三、来历四、举例说明一、前言 我第一次见到消融实验(Ablation Study)这个概念是在论文《Faster R-CNN》中。 消融实验类似于我们熟悉的“控制变量法”。 假设在某目标检测系统中,使用了A,B࿰…...

Java毕业论文参考文献参考例子整理
[1]李庆民.基于java的软件agent开发环境的分析[J].数字技术与应用,2017,01:189. [2]籍慧文.Web应用开发中JAVA编程语言的应用探讨[J].科技创新与应用,2017,07:90. [3]卜令瑞.基于Java软件项目开发岗位的企业实践总结报告[J].职业,2016,32:124-125. [4]肖成金,吕…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
