代码随想录算法训练营第43天:动态规划part10:子序列问题
300.最长递增子序列
力扣题目链接(opens new window)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
- 输入:nums = [10,9,2,5,3,7,101,18]
- 输出:4
- 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
子序列问题分析:
dp[i]的定义
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
注意**:概括来说:不连续递增子序列的跟前0-i 个状态有关,连续递增的子序列只跟前一个状态有关——这也是考虑如何构建动态规划算法的方法
- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
int lengthOfLIS(int* nums, int numsSize) {int dp[numsSize];dp[0]=1;int max_ans=1;//结果不一定在最后一个位置for (int i=1;i<numsSize;i++){dp[i]=1;//为什么要初始化成1:包含自己必然是最大的子序列,尤其是涉及到fmax,不能随便初始化的for (int j=0;j<i;j++){if(nums[j]<nums[i]) dp[i]=fmax(dp[i],dp[j]+1);}printf("%d",dp[i]);max_ans=fmax(max_ans, dp[i]);}return max_ans;
}674. 最长连续递增序列
力扣题目链接(opens new window)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
- 输入:nums = [1,3,5,4,7]
- 输出:3
- 解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
- 输入:nums = [2,2,2,2,2]
- 输出:1
- 解释:最长连续递增序列是 [2], 长度为1。
可以不用动态规划直接做:贪心 o(n) o(1)复杂度
int findLengthOfLCIS(int* nums, int numsSize) {int max_ans=1;int this=1;for (int i=1;i<numsSize;i++){if(nums[i]>nums[i-1]) {this++;max_ans=fmax(this, max_ans);} else {this=1;}}return max_ans;
}感觉动规做法过于复杂:
int findLengthOfLCIS(int* nums, int numsSize) {int max_ans=1;int dp[numsSize];dp[0]=1;for (int i=1;i<numsSize;i++){dp[i]=1;if(nums[i]>nums[i-1]) dp[i]=dp[i-1]+1;max_ans=fmax(max_ans, dp[i]);}return max_ans;
}718. 最长重复子数组
力扣题目链接(opens new window)
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:长度最长的公共子数组是 [3, 2, 1] 。
提示:
- 1 <= len(A), len(B) <= 1000
- 0 <= A[i], B[i] < 100
分析:
dp【i】【j】:是以i位置、j位置为结尾的匹配的情况——所以只和左上位置元素相关
之前考虑的时候,考虑成i位置、j位置以前的匹配的最大值情况,发现没有办法从上一个状态推导到这个状态——优先直接出结果,如果不能出结果,可以退而求其次,最大值的任务落在max_ans
上,优先考虑本次状态的情况
int findLength(int* nums1, int nums1Size, int* nums2, int nums2Size) {int dp[nums1Size][nums2Size];memset(dp,0, sizeof(dp));if(nums1[0]==nums2[0]) dp[0][0]=1;int max_ans=0;for (int i=1;i<nums1Size;i++){if(nums2[0]==nums1[i]) dp[i][0]=1;max_ans=fmax(max_ans, dp[i][0]);}for (int j=1;j<nums2Size;j++){if(nums1[0]==nums2[j]) dp[0][j]=1;max_ans=fmax(max_ans, dp[0][j]);}for (int i=1;i<nums1Size;i++){for (int j=1;j<nums2Size;j++){if(nums1[i]==nums2[j]) dp[i][j]=dp[i-1][j-1]+1;max_ans=fmax(max_ans, dp[i][j]);}}return max_ans;}相关文章:

代码随想录算法训练营第43天:动态规划part10:子序列问题
300.最长递增子序列 力扣题目链接(opens new window) 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2…...

传智教育引通义灵码进课堂,为技术人才教育学习提效
7 月 17 日,阿里云与传智教育在阿里巴巴云谷园区签署合作协议,双方将基于阿里云智能编程助手通义灵码在课程共建、品牌合作及产教融合等多个领域展开合作,共同推进 AI 教育及相关业务的发展,致力于培养适应未来社会需求的高素质技…...
企业信息化建设搞得好了叫系统工程,搞不好叫面子工程
2024-06-13 09:26贝格前端工场...

程序员如何平衡日常编码工作与提升式学习?
在快速变化的编程领域中,平衡日常编码工作与个人成长确实是一个重要且富有挑战性的议题。以下是我对这一问题的看法和建议: 1. 认识到平衡的重要性 首先,理解两者之间的平衡并非零和游戏,而是相辅相成的。高效的编码工作能够为个…...

Linux---文件系统和日志分析
文章目录 文件系统和日志分析inode和block概述inode包含文件的元信息用stat命令可以查看某个文件的inode信息Linux系统文件三个主要的时间属性 目录文件的结构用户通过文件名打开文件时,系统内部的过程查看inode号码的方法硬盘分区后的结构访问文件的简单流程inode的…...

MySQL 体系架构
文章目录 一. MySQL 分支与变种1. Drizzle2. MariaDB3. Percona Server 二. MySQL的替代1. Postgre SQL2. SQLite 三. MySQL 体系架构1.连接层2 Server层(SQL处理层)3. 存储引擎层1)MySQL官方存储引擎概要2)第三方引擎3࿰…...

跨站脚本攻击漏洞
1.JavaScript JavaScript 是一种脚本,一门编程语言,它可以在网页上实现复杂的功能,网页展现给你的不再是简单的静态信息,而是实时的内容更新,交互式的地图,2D/3D动画,滚动播放的视频等等。 &a…...
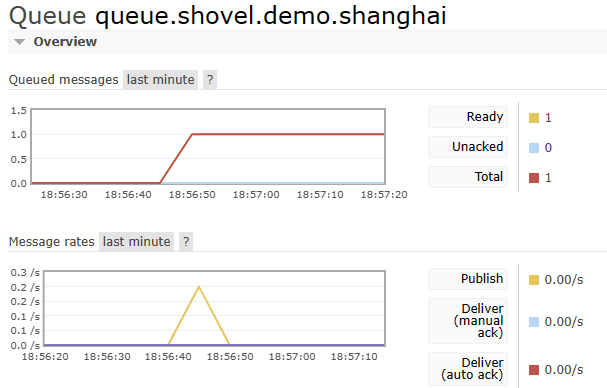
RabbitMQ入门与进阶
RabbitMQ入门与进阶 基础篇1. 为什么需要消息队列?2. 什么是消息队列?3. RabbitMQ体系结构介绍4. RabbitMQ安装5. HelloWorld6. RabbitMQ经典用法(工作模式)7. Work Queues8. Publish/Subscribe9. Routing10. Topics 进阶篇1. RabbitMQ整合SpringBoot2. 消息可靠性投递故障情…...

Unity新输入系统 之 InputActions(输入配置文件)
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 首先你应该了解新输入系统的基本单位Unity新输入系统 之 InputAction(输入配置文件最基本的单位࿰…...

Linux运维篇-误删/bin,/sbin目录怎么修复系统
这里写自定义目录标题 前言实例挂载镜像,重启系统进入救援模式拷贝镜像系统中的/bin和/sbin目录到原系统重启系统 总结 前言 当你看到这篇文章的时候,你的系统可能已经无法登录,或者正在处于登录状态但是不能执行任何常规的命令,…...

构建高效外贸电商系统的技术探索与源码开发
在当今全球化的经济浪潮中,外贸电商作为连接国内外市场的桥梁,其重要性日益凸显。一个高效、稳定、功能全面的外贸电商系统,不仅能够助力企业突破地域限制,拓宽销售渠道,还能提升客户体验,增强品牌竞争力。…...

Java设计模式:中介者模式详解与最佳实践
Java设计模式:中介者模式详解与最佳实践 1. 引言 在软件开发过程中,特别是复杂系统的构建中,模块间的交互往往成为影响代码质量的重要因素。当模块之间耦合度过高时,系统的维护、扩展和理解成本都会显著增加。为了降低模块之间的…...

Matlab绘制像素风字母颜色及透明度随机变化动画
本文是使用 Matlab 绘制像素风字母颜色及透明度随机变化动画的教程 实现效果 实现代码 如果需要更改为其他字母组合,在下面代码的基础上简单修改就可以使用。 步骤:(1) 定义字母形状;(2) 给出字母组合顺序;(3) 重新运行程序&#…...

C:每日一题:二分查找
1、知识介绍: 1.1 概念: 二分查找是一种在有序数组中查找某一特定元素的搜索算法 1.2 基本思想: 每次将待查找的范围缩小一半,通过比较中间元素与目标元素的大小,来决定是在左半部分还是右半部分继续查找。 举个生…...

python Django中使用ORM进行分组统计并降序排列
python Django中使用ORM进行分组统计并降序排列 # 使用supplier和Count进行分组统计,其中supplier为MyModel的一个字段 supplier_counts MyModel.objects.values(supplier).annotate(countCount(supplier)).order_by(-count) # 输出统计结果 for supplier_count in supplier_…...

QT C++ 编写modbus 总结
[开源库的使用]libModbus编译及使用_libmodbus库-CSDN博客 libmodbus的下载与编译_modbus库文件下载-CSDN博客 【QT5】解决 QT 界面中文显示乱码问题_qt5输出中文乱码解决方法-CSDN博客 Qt:解决qt修改完ui文件起不到作用_qt ui文件修改后不生效-CSDN博客...

基于SpringBoot的网络海鲜市场系统的设计与实现
TOC springboot219基于SpringBoot的网络海鲜市场系统的设计与实现 绪论 1.1 选题背景 当人们发现随着生产规模的不断扩大,人为计算方面才是一个巨大的短板,所以发明了各种计算设备,从结绳记事,到算筹,以及算盘&…...

c#相关基础知识
c#参数4种种别 值参:像Java的正常数据的传输 ref:对参数的指向是参数本身的地址,而不是数据的副本,所以可以对数据进行直接操作 out: 绑定控件,控件传输值赋值给类中的内部类 待定...

注意力机制 — 它是什么以及它是如何工作的
一、说明 注意力机制是深度学习领域的一个突破。它们帮助模型专注于数据的重要部分,并提高语言处理和计算机视觉等任务的理解和性能。这篇文章将深入探讨深度学习中注意力的基础知识,并展示其背后的主要思想。 二、注意力机制回顾 在我们谈论注意力之前&…...

学习嵌入式第二十六天
进程线程 1.进程的概念 2.进程 和 程序 硬盘中程序 ,加载到内存中,运行起来,就是进程 创建线程 pthread_create posix thread create 线程执行 ---体现在线程执行函数 (回调函数) 线程退出 ---pthread_exit() …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...
