回归分析系列1-多元线性回归
03 多元线性回归
3.1 简介
多元线性回归是简单线性回归的扩展,允许我们同时研究多个自变量对因变量的影响。多元回归模型可以表示为:
其中,x1,x2,…,xp是 p 个自变量,β0 是截距,β1,β2,…,βp是对应的回归系数,ϵ是误差项。
3.2 估计回归系数
类似于简单线性回归,多元线性回归的系数估计也通常使用最小二乘法。我们选择回归系数,使得实际观测值与模型预测值之间的残差平方和最小。
在Python中,我们可以使用statsmodels库来拟合多元线性回归模型。下面是一个示例代码:
import numpy as np
import pandas as pd
import statsmodels.api as sm# 生成模拟数据
np.random.seed(0)
X = np.random.rand(100, 2) # 100个样本,每个样本有2个自变量
y = 2 + 3 * X[:, 0] + 5 * X[:, 1] + np.random.randn(100) # 因变量# 拟合多元线性回归模型
X = sm.add_constant(X) # 添加截距项
model = sm.OLS(y, X).fit()# 输出回归结果
print(model.summary())
在这个例子中,我们生成了两个自变量,并通过多元线性回归模型来估计它们对因变量的影响。
3.3 模型拟合与解释
多元线性回归的拟合结果包含多个回归系数,每个系数反映了对应自变量对因变量的影响。通过这些系数,我们可以判断每个自变量在控制其他变量的情况下对因变量的边际影响。
例如,如果我们在模型中包含了两个自变量 x1和 x2,我们可以解释回归系数表示在 x2不变的情况下,x1 每增加一个单位,y 增加的量。
3.4 假设检验与模型选择
在多元回归分析中,我们通常会进行假设检验来评估每个自变量的显著性。我们通常检验的假设是 H0:=0,即某个自变量对因变量没有显著影响。
在Python中,statsmodels 的回归结果会自动提供每个回归系数的 t 值和 p 值,这些值可以帮助我们进行假设检验。
此外,我们还可以使用 AIC(Akaike Information Criterion)和 BIC(Bayesian Information Criterion)等信息准则来比较不同模型的拟合效果,从而选择最佳模型。
3.5 多重共线性
多元回归模型的一个潜在问题是多重共线性,即自变量之间存在较高的相关性。这可能导致估计的回归系数不稳定,并且使得模型对数据中的噪声过于敏感。
为了检测多重共线性,我们可以计算方差膨胀因子(Variance Inflation Factor, VIF)。VIF值越高,表明自变量之间的相关性越强,通常VIF大于10被认为是共线性较强的标志。
在Python中,可以使用statsmodels库的variance_inflation_factor函数来计算VIF值:
from statsmodels.stats.outliers_influence import variance_inflation_factor# 计算VIF值
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X, i) for i in range(X.shape[1])]
vif["features"] = ["const", "x1", "x2"]print(vif)
通过这个表格,我们可以识别出具有高VIF值的自变量,并考虑是否需要对模型进行调整,例如通过去除变量或使用正则化技术。
3.6 模型诊断
在多元线性回归中,模型诊断与简单线性回归类似,但也存在一些特有的挑战。我们依然需要检查残差的正态性、同方差性和独立性,同时还需要关注多重共线性和异常点的影响。
残差正态性
残差的正态性是最小二乘估计量的一个重要假设。可以通过绘制QQ图来检验残差是否服从正态分布。
import matplotlib.pyplot as plt
import scipy.stats as stats# 绘制QQ图
sm.qqplot(model.resid, line='s')
plt.show()
残差同方差性
同方差性假设要求残差的方差在不同的自变量值上保持恒定。可以通过绘制残差与预测值的散点图来检验这一假设。
# 绘制残差与预测值的散点图
plt.scatter(model.fittedvalues, model.resid)
plt.axhline(y=0, color='r', linestyle='-')
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.show()
如果残差图显示出漏斗形状,则可能存在异方差性。
多重共线性
如前所述,多重共线性会导致回归系数的不稳定,影响模型的解释性。除了使用VIF值外,我们还可以通过观察回归系数的变化来识别共线性问题。
异常值与杠杆点
异常值和杠杆点可能会对模型产生过大的影响。可以通过Cook’s距离来识别这些点。
influence = model.get_influence()
cooks = influence.cooks_distance[0]plt.stem(np.arange(len(cooks)), cooks, markerfmt=",")
plt.title('Cook\'s Distance')
plt.show()
如果某些点的Cook’s距离特别大,则表明它们可能对模型拟合有不成比例的影响。
3.7 高维数据中的回归
在实际应用中,自变量的数量有时可能远多于观测值的数量。这种情况下,传统的最小二乘回归可能不适用,因为模型会出现过拟合问题,预测能力下降。为了解决这一问题,通常采用以下方法:
岭回归
岭回归通过在最小二乘目标函数中添加一个惩罚项来抑制回归系数的大小,从而减小多重共线性问题对模型的影响。这个惩罚项通常是回归系数的平方和的某个倍数。
from sklearn.linear_model import Ridge# 拟合岭回归模型
ridge_model = Ridge(alpha=1.0) # alpha为正则化参数
ridge_model.fit(X[:, 1:], y) # 注意在这里我们不包含截距项# 输出回归系数
print(ridge_model.coef_)
Lasso回归
Lasso回归(Least Absolute Shrinkage and Selection Operator)也通过增加一个惩罚项来限制回归系数的绝对值,从而可以进行变量选择,即将不重要的变量系数缩为零。
from sklearn.linear_model import Lasso# 拟合Lasso回归模型
lasso_model = Lasso(alpha=0.1)
lasso_model.fit(X[:, 1:], y)# 输出回归系数
print(lasso_model.coef_)
弹性网回归
弹性网回归结合了岭回归和Lasso回归的惩罚项,适用于特征之间高度相关的情况。
from sklearn.linear_model import ElasticNet# 拟合弹性网回归模型
elastic_net_model = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net_model.fit(X[:, 1:], y)# 输出回归系数
print(elastic_net_model.coef_)
3.8 示例:犯罪率与社会经济因素
让我们通过一个具体的例子来理解多元线性回归。在这个例子中,我们研究一个数据集,探索城市中的犯罪率与一系列社会经济因素之间的关系。假设我们有以下变量:
- 犯罪率(因变量)
- 城市人口密度
- 城市中的失业率
- 平均收入
我们可以通过以下代码来加载数据并拟合多元线性回归模型:
# 假设我们有一个数据框包含以上变量
data = pd.DataFrame({'crime_rate': np.random.rand(100),'population_density': np.random.rand(100),'unemployment_rate': np.random.rand(100),'average_income': np.random.rand(100)
})# 定义自变量和因变量
X = data[['population_density', 'unemployment_rate', 'average_income']]
y = data['crime_rate']# 添加截距项
X = sm.add_constant(X)# 拟合多元线性回归模型
model = sm.OLS(y, X).fit()# 输出回归结果
print(model.summary())
这个模型将帮助我们理解不同社会经济因素如何共同影响犯罪率。通过观察回归系数和p值,我们可以识别出哪些因素对犯罪率有显著影响。
相关文章:
回归分析系列1-多元线性回归
03 多元线性回归 3.1 简介 多元线性回归是简单线性回归的扩展,允许我们同时研究多个自变量对因变量的影响。多元回归模型可以表示为: 其中,x1,x2,…,xp是 p 个自变量,β0 是截距,β1,β2,…,βp是对应的回归系数&…...

web小游戏开发:拼图——蜂巢拼图
web小游戏开发:拼图——蜂巢拼图 蜂巢拼图游戏规则调整选项切图计算六边形的宽和高铺上背景画出蜂巢制作图块游戏方法打乱排列拖拽图块开始拖拽拖拽移动放置图块小结蜂巢拼图 之前我们已经完成了长方形的拼图代码,包括了三个游戏方式,并讨论了带咬合齿的游戏代码该如何制作…...

springCloud集成activiti5.22.0流程引擎(分支)
springCloud集成activiti5.22.0流程引擎 点关注不迷路,欢迎再访! 精简博客内容,尽量已行业术语来分享。 努力做到对每一位认可自己的读者负责。 帮助别人的同时更是丰富自己的良机。 文章目录 springCloud集成activiti5.22.0流程引擎一.Sprin…...
ppt模板免费网站有哪些?自动美化工具推荐
新的8月,是时候以全新面貌迎接高效办公挑战了! 想要你的PPT演示脱颖而出,却苦于找不到精美又免费的模板? 别担心,今天我来告诉你们:哪个软件有精美免费ppt模板? 今天我为你们精心汇总了6款PPT…...

java实现解析pdf格式发票
为了减少用户工作量及误操作的可能性,需要实现用户上传PDF格式的发票,系统通过解析PDF文件获取发票内容,并直接将其写入表单。以下文章记录了功能实现的代码。 发票样式 发票内容解析 引用Maven 使用pdfbox <dependency><groupI…...

数据结构初阶——算法复杂度超详解
文章目录 1. 数据结构前言1. 1 数据结构1. 2 算法 2. 算法效率2. 1 复杂度的概念 3. 时间复杂度3. 1 大O的渐进表示法3. 2 时间复杂度计算示例3. 2. 1 示例13. 2. 2 示例23. 2. 3 示例33. 2. 4 示例43. 2. 5 示例53. 2. 6 示例63. 2. 7 示例7 4. 空间复杂度4. 1 空间复杂度计算…...
布局 4 预定义的形状和箭头)
ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头
ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头 文章目录 ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头1 创建预定义的形状图形元素2 创建预定义的形状图形元素3 创建预定义的形状图形元素4 创建线箭头元素环境:Visual Studio 2022 + .NET6 + ArcGIS Pro SDK 3.0 1 …...

在 Ubuntu 14.04 服务器上安装 ISPConfig3 的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 虽然命令行是一个强大的工具,可以让您在许多情况下快速轻松地工作,但在某些情况下,可视化界面…...

ELK学习笔记
ElasticStack分布式日志系统概述 Elasticsearch: 一个分布式搜索引擎,能够快速存储、搜索和分析大量数据。核心概念包括索引(Index)、文档(Document)和分片(Shard)。使用 RESTful API 进行数据操…...
Python+Selenium+Pytest+POM自动化测试框架封装详解
1、测试框架简介 1)测试框架的优点 代码复用率高,如果不使用框架的话,代码会显得很冗余。可以组装日志、报告、邮件等一些高级功能。提高元素等数据的可维护性,元素发生变化时,只需要更新一下配置文件。使用更灵活的…...

Hidden Marlov Model(HMM)
一、Model 1、将声学特征设为X,经过语音识别得到的tokens设为Y,目标是找到通过X得到Y的最大概率,可以通过概率公式改变为 分为两个概率 2、将tokens序列Y转化为states序列S,声学特征分得更细 3、从states到声学特征的过程 二、HM…...

mamba的安装及下载速度慢问题解决
同事反馈mamba的安装时网络慢 mamba是conda的加速工具,相比于conda 对包和环境的管理,mamba可以实现并行运算。相比于 conda,mamba 是用C重写了 conda 的部分功能,运行效率显著提高,可以进行并行的下载,使…...
【Linux入门】Linux环境搭建
目录 前言 一、发行版本 二、搭建Linux环境 1.Linux环境搭建方式 2.虚拟机安装Ubuntu 22.02.4 1)安装VMWare 2)下载镜像源 3)添加虚拟机 4)换源 5)安装VM Tools 6)添加快照 总结 前言 Linux是一款自由和开放…...

CPU缓存一致性机制详解
CPU缓存一致性机制详解 在多核处理器中,缓存一致性是保证系统正常运行的重要环节。本文详细介绍了缓存一致性协议、写入策略、总线嗅探、目录协议等相关概念,并通过示例代码解释了这些机制是如何在实际应用中工作的。通过学习本文,读者可以深…...

Android 12系统源码_屏幕设备(一)DisplayManagerService的启动
前言 DisplayManagerService是Android Framework中管理显示屏幕相关的模块,各种Display的连接、配置等,都是通过DMS和来管理控制。 在DMS模块中,对显示屏幕的描述分为物理显示屏(physical display)和逻辑显示屏(logical display),…...

《AI视频类工具之十——D-ID》
一.简介 官网:D-ID | The #1 Choice for AI Generated Video Creation Platform D-ID是一个人工智能生成的视频创建平台,可以轻松快速地从文本输入中创建高质量、高性价比和引人入胜的视频,背后的Al技术是由Stable Difusion和GPT.3提供支持,可以在没有任何技术知识的情况…...
【网络】局域网LAN、广域网WAN、TCP/IP协议、封装和分用
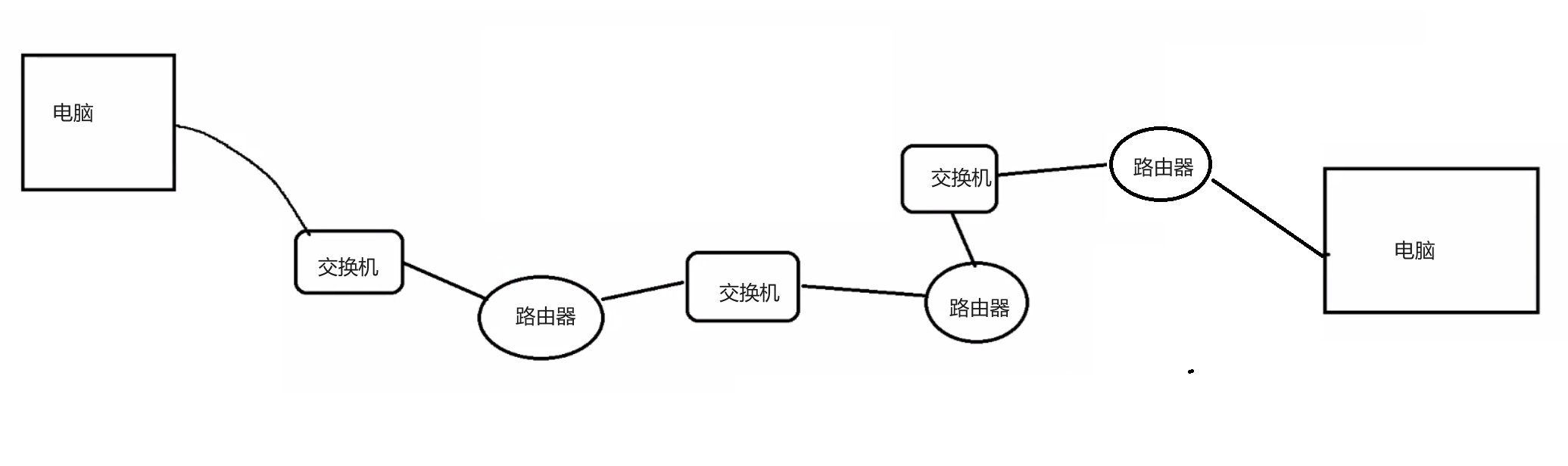
文章目录 局域网 LAN广域网 WAN网络中的重要概念IP 地址端口号 认识协议协议分层是什么OSI 七层网络模型TCP/IP 五层网络模型(或四层)物理层传输层网络层数据链表层应用层网络设备所在分层 封装和分用[站在发送方视角](封装)[站在…...

我司搜索中台的三次演变
本人从入职就开始负责我司的搜索中台了,总共是经历了三个大版本的迭代。 分别是: 基于阿里云智能开放搜索OpenSearch实现的第一代自研,开源canal(数据同步) 底层阿里云elasticsearch 对索引封装 实现的第二代自研&a…...

html+css+js网页设计 电商模版4个页面
htmlcssjs网页设计 电商模版4个页面 带js 网页作品代码简单,可使用任意HTML编辑软件(如:Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑等操作)。 获取源码 1&…...

区块链技术在Facebook中的潜力:未来趋势与挑战
数据安全的新高度 区块链技术以其去中心化和不可篡改的特性,正在成为提升数据安全和隐私保护的重要工具。Facebook作为全球最大的社交媒体平台之一,正积极探索如何将区块链技术应用于其平台,以增强用户数据的安全性和隐私保护。Facebook在应…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
