c++实现B树(上)
哈喽啊!好久不见,甚是想念!失踪人口要回归了,时隔一个多月小吉我终于要更新blog了🎉。在停更的一个多月中,小吉也有在好好学习提升自己,立志给大家呈现好文章。
现在让我们进入正题吧,今天我们这篇blog主要讲用c++实现B树,上一篇blog讲的是二叉搜索树,中间还有avl树和红黑树小吉还没有把博客写出来。希望大家多多关注小吉,在完成这篇blog后,小吉将会出avl树实现的博客(浅浅期待一下吧)。
老规矩,在正式实现B树之前,我们先来了解了解什么是B树。
B树的概念
B树:B树是一种自平衡的树形数据结构,用于解决磁盘存储器上的数据管理问题,减少磁盘i/o操作的次数,从而提高数据访问的效率。
B树的特征
在讲B树的特征之前,我们先来了解一下度和阶的概念
度(degree):指树中节点孩子数
阶(order):指所有节点孩子数最大值
在m阶的B树中,即孩子数最大值为m
B树的特征
1.B树的每个节点可以有多个子结点,每个节点最多可以有m个子节点;除根节点和叶子节点外,其他每个节点至少有ceil(m/2)个孩子。(ceil是指向上取整)
2.每个节点的关键字(键值)数量与子节点数量相关,通常比子节点数量少1。每个节点中的关键字数量k满足ceil(m/2)-1<=k<=m-1。
3.B树的所有叶子节点都在同一层
4.B树通过动态调整节点中的关键字数量来保持树的平衡
5.B树中的关键字按照升序排序
6.父节点中第i个关键字小于其第i个子节点的所有关键字,且大于其第i-1个子节点中所有的关键字

(小吉在这里提醒一下:一定要好好理解B树的特征,后面在实现的过程有什么不能理解的地方,一定要回头好好读一下特征,大部分问题都能在看过特征后得到解答(小吉的小经验✨))
B树节点类
_t代表最小度数,也就是最小的孩子数ceil(m/2),因此最大孩子数m可以由2*t表示
节点类代码呈现👇:
class Node
{
public:Node(int t, bool leaf = true) :_t(t), _leaf(left), _children(2 * t, nullptr),_keys(2*t-1),KeyNumber(0){}//初始化列表
public:vector<int> _keys;//键值vector<Node*> _children;//孩子int KeyNumber;//有效键值数目bool _leaf;//是否为叶子节点int _t;//最小度数(最小孩子数)
};
B树节点类成员方法
主要实现3个方法
1.Node* get(int key);//多路查找
2.void insertKey(int index,int key);//向指定索引处插入key
3.void insertChild(int index, Node* child);//向指定索引处插入child
代码呈现👇:
Node* Node::get(int key)
{int i = 0;while (i < KeyNumber){if (_keys[i] == key){return this;}if (_keys[i] > key){break;}i++;}//比key值大且为叶子节点if (this->_leaf){return nullptr;}//非叶子节点(采用递归)return _children[i]->get(key);
}
void Node::insertKey(int index,int key)
{_keys.insert(_keys.begin() + index, key);KeyNumber++;
}
void Node::insertChild(int index, Node* child)
{_children.insert(_children.begin() + index, child);
}
B树类
class BTree
{
public:BTree(int t) :_t(t), _root(new Node(t)), MAX_KEYNUMS(2 * t - 1), MIN_KEYNUMS(t - 1) { }//初始化列表
public:Node* _root;int _t;//树中最小度数const int MIN_KEYNUMS;const int MAX_KEYNUMS;
};
注意:const成员变量必须在构造函数的初始化列表中进行初始化,而不能在构造函数体内部通过赋值语句来初始化
B树类成员方法
bool contains(int _key);//判断节点是否存在
代码实现👇:
//是否存在bool contains(int _key){return _root->get(_key) != nullptr;}
B树put插入节点初实现
put实现思路:
1.首先查找本节点中的插入位置,如果没有空位(key被找到),应该走更新的逻辑
2.如果找到空位,该节点是叶子节点,可以直接插入;该节点是非叶子节点,需要继续在children[i]处继续递归插入
代码架构👇:
void BTree::doput(Node* node, int key,Node* parent,int index)
{int i = 0;while (i < node->KeyNumber){if (node->_keys[i]==key){node->_keys[i] = key;//更新return;}if (node->_keys[i] > key){break;//找到了插入位置}i++;}if (node->_leaf){node->insertKey(i, key);}else{doput(node->_children[i], key,node,i);//递归}
}
void BTree::put(int key)
{doput(_root, key,nullptr,0);
}
B树split分裂
无论哪种情况,插入完成后都可能超过节点keys数目限制,应执行节点分裂

(注:较小的数字代表索引)
void BTree::split(Node* left, Node* parent, int index)
left为待分裂节点,index是该待分裂节点作为孩子的索引
split分裂思路🎇
1.创建right节点(分裂后大于当前left节点的),把t(最小孩子数)以后的key和child都拷贝过去
2.t-1处的key插入到parent的index处(index指left作为孩子时的索引)
3.right节点作为parent的孩子插入到index+1处
分为三种情况,待分裂节点为叶子节点,非叶子节点和根节点。1️⃣我们先来实现最简单的一种情况,待分裂节点为叶子节点。
代码展示👇:
void BTree::split(Node* left, Node* parent, int index)
{
//1.创建right节点,把left中t之后的key和child移动过去Node* right = new Node(_t);right->_leaf = left->_leaf;right->_keys.assign(left->_keys.begin() + _t, left->_keys.end());right->KeyNumber = _t - 1;left->KeyNumber = _t - 1;//2.中间的key(t-1处)插入到父节点int mid = left->_keys[_t - 1];parent->insertKey(index, mid);//3.right节点作为父节点的孩子parent->insertChild(index + 1, right);
}
实现叶子节点的分裂就按照上面的思路就可以了,相对比较简单,我们现在可以小小测试一下代码,这里提供一个小的测试案例
void splitTest()//split分裂方法的测试案例
{BTree tree(2);Node* root = tree._root;root->_leaf = false;root->_keys[0] = 2;root->KeyNumber = 1;root->_children[0] = new Node(2);root->_children[0]->_keys = { 1 };root->_children[0]->KeyNumber = 1;root->_children[1] = new Node(2);root->_children[1]->_keys = { 3,4,5 };root->_children[1]->KeyNumber = 3;tree.split(root->_children[0], root, 0);
}
分裂结果可以参照小吉上面给的图
2️⃣待分裂节点为非叶子节点,这种情况就比叶子节点多一个步骤就是处理孩子
代码实现👇:
void BTree::split(Node* left, Node* parent, int index)
{
//1.创建right节点,把left中t之后的key和child移动过去Node* right = new Node(_t);right->_leaf = left->_leaf;right->_keys.assign(left->_keys.begin() + _t, left->_keys.end());//分裂节点是非叶子节点的情况if (!left->_leaf){right->_children.assign(left->_children.begin() + _t, left->_children.end());}right->KeyNumber = _t - 1;left->KeyNumber = _t - 1;//2.中间的key(t-1处)插入到父节点int mid = left->_keys[_t - 1];parent->insertKey(index, mid);//3.right节点作为父节点的孩子parent->insertChild(index + 1, right);
}
3️⃣待分裂节点为根节点,这里小吉先画个图来帮小可爱们想象一下

思路:如果parent==nullptr表示要分裂的是根节点,此时需要创建新根,原来的根节点作为新根的0(索引)孩子
代码实现👇:
if (parent == nullptr)//分裂的是根节点{Node* newRoot = new Node(_t);newRoot->_leaf = false;newRoot->insertChild(0, left);this->_root = newRoot;parent = newRoot;}
三种情况已经全部分析完了🎉🎉🎉,现在小吉把三种情况的代码进行汇总,封装在split方法中
void BTree::split(Node* left, Node* parent, int index)
{if (parent == nullptr)//分裂的是根节点{Node* newRoot = new Node(_t);newRoot->_leaf = false;newRoot->insertChild(0, left);this->_root = newRoot;parent = newRoot;}//1.创建right节点,把left中t之后的key和child移动过去Node* right = new Node(_t);right->_leaf = left->_leaf;right->_keys.assign(left->_keys.begin() + _t, left->_keys.end());//分裂节点是非叶子节点的情况if (!left->_leaf){right->_children.assign(left->_children.begin() + _t, left->_children.end());}right->KeyNumber = _t - 1;left->KeyNumber = _t - 1;//2.中间的key(t-1处)插入到父节点int mid = left->_keys[_t - 1];parent->insertKey(index, mid);//3.right节点作为父节点的孩子parent->insertChild(index + 1, right);
}
节点的分裂到这里已经全部讲完了🥳🥳🥳,下面就是要把split方法和put方法结合起来
B树put插入节点最终实现
思路:叶子节点加入key时要做分裂的检查,当节点中的有效键值数等于最大键值数时要进行节点的分裂
void BTree::put(int key)
{doput(_root, key,nullptr,0);
}void BTree::doput(Node* node, int key,Node* parent,int index)
{int i = 0;while (i < node->KeyNumber){if (node->_keys[i]==key){node->_keys[i] = key;//更新return;}if (node->_keys[i] > key){break;//找到了插入位置}i++;}if (node->_leaf){node->insertKey(i, key);}else{doput(node->_children[i], key,node,i);//递归}if (node->KeyNumber == MAX_KEYNUMS)//进行分裂{split(node, parent, index);}
}
这篇blog到这里已经全部结束了,浅浅预告一下小吉的下一篇blog讲的是B树的删除操作(又是一个大工程😶🌫️),还望大家多多支持小吉❤️
这篇博客有点长也有点难,希望小可爱们给自己多一点耐心,静下心来慢慢学,还有一定要敲代码,只有敲了代码才能发现问题。
创作不易,还望大家多多支持🌹🌹🌹(小吉写了整整3个小时🤣)
相关文章:

c++实现B树(上)
哈喽啊!好久不见,甚是想念!失踪人口要回归了,时隔一个多月小吉我终于要更新blog了🎉。在停更的一个多月中,小吉也有在好好学习提升自己,立志给大家呈现好文章。 现在让我们进入正题吧…...

【机器学习】深度强化学习–RL的基本概念、经典场景以及算法分类
引言 深度强化学习(Deep Reinforcement Learning, DRL)是机器学习的一个分支,它结合了深度学习(Deep Learning)和强化学习(Reinforcement Learning, RL)的技术 文章目录 引言一、深度强化学习–…...

【git】将本地文件上传到github
安装git 选择一个文件夹作为git仓库,cd到文件夹输入 git init文件夹出现.git文件夹,该文件夹默认为隐藏文件夹,设置为不隐藏 在cmd中输入 ssh-keygen -t rsa -C "xxxxxx.com"该邮箱为github邮箱,然后一路enter出现以…...

安卓应用开发学习:手机摇一摇功能应用尝试--摇骰子和摇红包
一、引言 前几天,我发布的日志《安卓应用开发学习:查看手机传感器信息》记录了如何查看手机传感器的信息,通过上述的方法,可以看到我的OPPO手机支持19种传感器。本篇日志就记录一下常见的加速度传感器的典型应用——“摇一摇”功…...

HTML中的<fieldset>标签元素框的使用
HTML 提供的 <fieldset> 标签用于在表单中分组相关元素。 <fieldset> 标签会在相关元素周围绘制一个框。 <legend> 标签为 fieldset 元素定义标题。 语法如下: <fieldset><legend>标题</legend><!-- 元素内容... -->…...
Linux驱动入门实验班——SR501红外模块驱动(附百问网视频链接)
目录 一、工作方式 二、接口图 三、编写思路 1.构造file_operations结构体 2.实现read函数 3.编写入口函数 4.编写中断处理函数 5.编写出口函数 6.声明出入口函数以及协议 四、源码 五、课程链接 一、工作方式 SR501人体红外感应模块有两种工作模式: …...
)
windows C++- Com技术简介(上)
在介绍C和winrt与COM组件技术的关系之前,有必要介绍一下com组件技术,这项技术比较古老,但是它一直作为windows的基石存在。COM 是一类独立于平台且面向对象的分布式系统,用于创建可交互的二进制软件组件。 COM 技术是 Microsoft O…...

Jenkins持续集成工具学习
一、从装修厨房看项目开发效率优化 二、持续集成工具 三、JavaEE项目部署方式对比 四、JenkinsSVN持续集成环境搭建 五、JenkinsGitHub持续集成环境搭建...

Redis:查询是否包含某个字符/字符串之三
上一篇:Redis:查询是否包含某个字符/字符串之二-CSDN博客 摘要: 遍历key,在跟进value的类型遍历value是否包含指定字符串 search_strings ,这里使用redis-py库,默认只能处理utf-8编码,如果存在…...
【Redis】数据类型详解及其应用场景
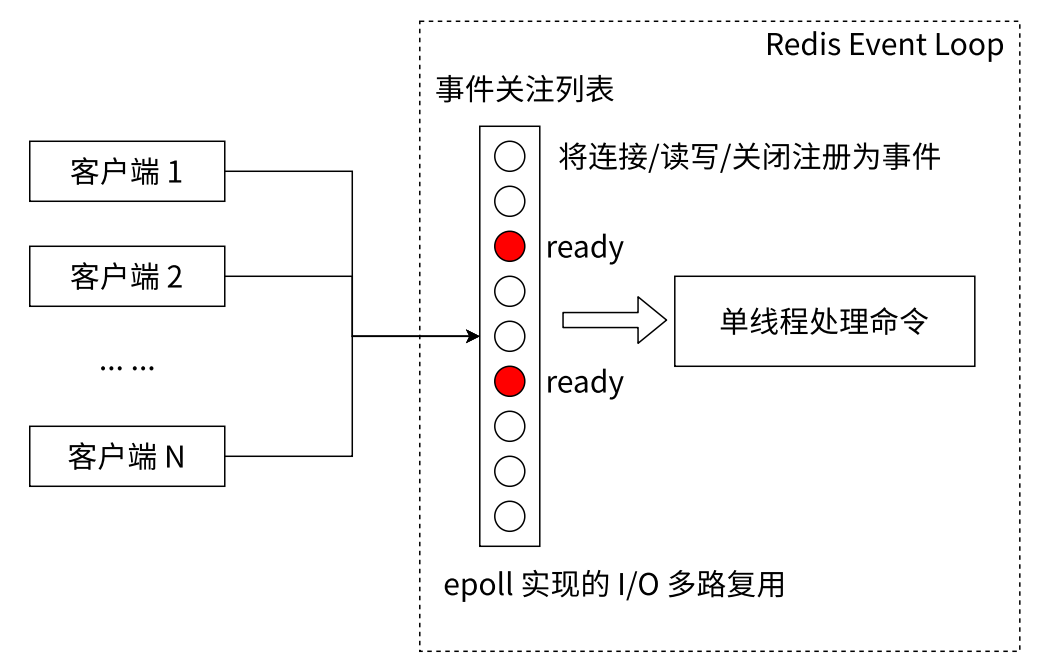
目录 Redis 常⻅数据类型预备知识基本全局命令小结 数据结构和内部编码单线程架构引出单线程模型为什么单线程还能这么快 Redis 常⻅数据类型 Redis 提供了 5 种数据结构,理解每种数据结构的特点对于 Redis 开发运维⾮常重要,同时掌握每种数据结构的常⻅…...

PARA-Drive:设计并行模型实现端到端自动驾驶
论文链接 https://openaccess.thecvf.com/content/CVPR2024/papers/Weng_PARA-Drive_Parallelized_Architecture_for_Real-time_Autonomous_Driving_CVPR_2024_paper.pdfhttps://openaccess.thecvf.com/content/CVPR2024/papers/Weng_PARA-Drive_Parallelized_Architecture_fo…...

vs2022 x64 C/C++和汇编混编 遇到的坑
vs2022 x64 C/C和汇编混编 遇到的坑 遇到的问题二、问题复现1.出错代码2.问题分析2.1 堆栈对齐问题 3.解决方案 总结奇数和偶数个寄存器的影响为什么 sub rsp, 8 对奇数个寄存器有用?结论 遇到的问题 0x00007FFFFAE24A29 (msvcp140.dll)处(位于 TestCompileConsole…...
PHP概述、环境搭建与基本语法讲解
目录 【学习目标、重难点知识】 什么是网站? 1. PHP 介绍 1.1. PHP 概述 1.1.1. PHP 是什么? 1.1.2. PHP 都能做什么? 1.2. PHP 环境搭建 1.2.1. PhpStudy 2. PHP 基本语法 2.1. PHP 语法入门 2.1.1. 第一个 PHP 程序 2.1.2. PHP …...
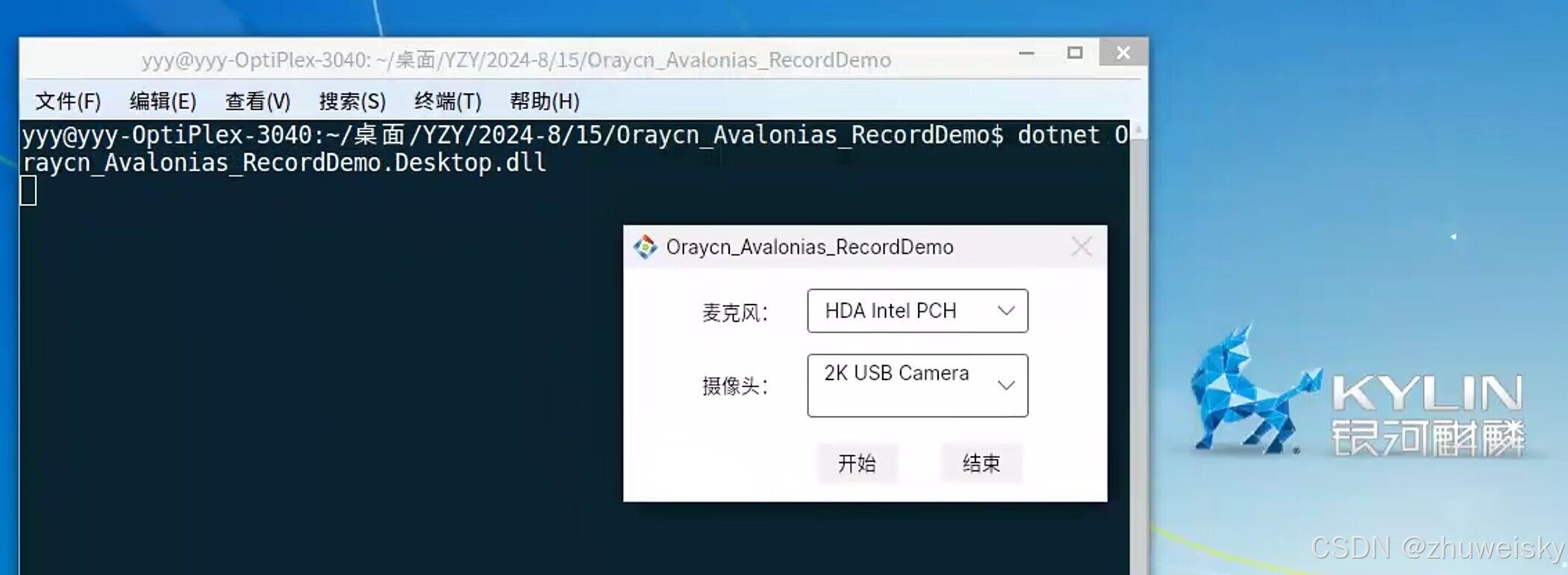
实现信创Linux麦克风摄像头录制(源码,银河麒麟、统信UOS)
随着信创国产化浪潮的来临,在国产操作系统上的应用开发的需求越来越多,其中一个就是需要在银河麒麟或统信UOS上实现录制摄像头视频和麦克风声音,将它们录制成一个mp4文件。那么这个要如何实现了? 一. 技术方案 要完成这些功能&a…...

深度学习9--目标检测
1.概念介绍 目标检测不仅可以检测数字,而且可以检测动物的种类、汽车的种类等。例如,自动驾驶车辆需要自动识别前方物体是车辆还是行人,需要自动识别道路两 旁的指示牌和前方的红绿灯颜色。对于自动检测的算法,有两个要求…...

第131天:内网安全-横向移动Kerberos 攻击SPN扫描WinRMWinRSRDP
案例一:域横向移动-RDP-明文&NTLM RDP利用的三种方式 1.直接在当前被控主机上进行远程连接 2.建立节点进行连接 3.端口转发,(访问当前主机的2222端口等于访问目标的3389) 第一种方式(动静太大) 直接利用被控主机进行远程连接…...

微信小程序的四种弹窗使用
在做小程序的过程中,弹窗也算是非常实用的功能了,这几天写的几个功能就用到了弹窗,也可能是初学者的问题,比较菜,想找一个可以带图片的自定义的弹窗,,这里简单介绍一下官方封装好的四个弹窗…...

我的第一个CUDA程序
MatAdd算法 实现两个矩阵对应元素相加 #include <stdio.h> #include <stdlib.h>// 矩阵加法函数 void MatAdd(int height, int width) {// 在主机内存中为 A、B 和 C 分配内存float* A (float*)malloc(height * width * sizeof(float));float* B (float*)malloc…...

workerman下的webman路由浏览器跨域的一种问题
软件版本 "php": ">7.2", "workerman/webman-framework": "^1.5.0",问题情景 使用“分组路由”做API接口前后端分离跨域,在接口测试工具调试是能正常获取数据的;但在网页浏览器上调试就遇到了CORS、404的错…...

Windows11 -MASKRCNN-部署测试
文章目录 Detectron2环境配置搭建python 环境安装Cuda \CUDNN 、PyTorch、 torchvision、cudatoolkit1、Cuda \CUDNN2、 PyTorch、 torchvision、cudatoolkit进入python测试:错误信息 3、detectron2环境在安装detecteron中,遇到报错:编译的时…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
