用Python实现9大回归算法详解——04. 多项式回归算法
多项式回归 是线性回归的一种扩展,它通过将输入特征的多项式项(如平方、立方等)引入模型中,以捕捉数据中非线性的关系。虽然多项式回归属于线性模型的范畴,但它通过增加特征的多项式形式,使得模型能够拟合非线性数据。
1. 多项式回归的基本概念与动机
1.1 为什么使用多项式回归?
在很多实际应用中,特征与目标变量之间的关系并不是简单的线性关系,而是更加复杂的非线性关系。虽然可以通过增加特征的数量来捕捉这种非线性关系,但有时直接将特征进行多项式扩展是更为自然的选择。
多项式回归通过引入原始特征的高次项来捕捉非线性关系。例如,如果 与
之间的关系是二次或三次关系,则线性回归可能无法很好地拟合数据,而多项式回归可以更准确地捕捉这种关系。
1.2 多项式回归的模型形式
对于一个变量 的二次多项式回归模型,其形式为:
对于 阶的多项式回归,模型形式为:
是目标变量。
是自变量。
是模型的回归系数。
是误差项。
1.3 多项式回归的动机
多项式回归的主要动机在于,通过增加特征的多项式项(如 等),可以在线性模型的框架内处理非线性关系。多项式回归仍然是线性模型,因为它对系数的求解是线性的,但它能够拟合非线性数据。
1.4 多项式回归的步骤
多项式回归的主要步骤如下:
- 特征扩展:将原始特征 xxx 扩展为多项式特征
。
- 线性回归:使用线性回归模型拟合扩展后的多项式特征。
- 模型预测:使用训练好的模型对新数据进行预测。
2. 多项式回归的数学推导与最小二乘法
2.1 特征扩展
假设我们有一个自变量 ,通过将其扩展为
,我们可以将原始的线性回归模型转化为多项式回归模型。
对于 阶多项式回归,模型形式为:
其中,。
2.2 损失函数的定义
与线性回归类似,多项式回归的目标也是最小化残差平方和。损失函数为:
其中:
是样本数。
是第
个样本的实际值。
是第
个样本的预测值,计算公式为:
2.3 最小二乘法求解
多项式回归与线性回归的本质相同,都是通过最小化损失函数来求解回归系数 。我们可以通过矩阵运算来求解:
其中:
是特征矩阵,形状为
。
是目标变量向量,形状为
。
是回归系数向量,形状为
。
3. 多项式回归的常见问题
3.1 过拟合问题
随着多项式阶数的增加,模型的复杂度也随之增加。虽然高阶多项式可以很好地拟合训练数据,但它们可能会捕捉到数据中的噪声,导致在测试数据上的泛化能力下降,即出现过拟合。
3.2 偏差-方差权衡
在选择多项式阶数时,需要在模型的偏差和方差之间进行权衡。低阶多项式模型可能存在较大的偏差,而高阶多项式模型可能存在较大的方差。理想情况下,我们希望选择一个合适的阶数,使得模型的偏差和方差都处于较低水平。
4. 多项式回归案例:捕捉非线性关系
接下来,我们通过一个具体的案例,展示如何使用多项式回归捕捉数据中的非线性关系。
4.1 数据生成与预处理
我们首先生成一个模拟数据集,包含 100 个样本,目标变量与自变量之间存在二次非线性关系。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression# 生成模拟数据
np.random.seed(42)
X = 2 - 3 * np.random.normal(0, 1, 100) # 100个样本
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100) # 二次非线性关系# 查看数据
df = pd.DataFrame({'Feature': X, 'Target': y})
print(df.head())
输出:
Feature Target
0 -0.496714 -2.562097
1 1.861735 -5.639160
2 -0.647689 0.682448
3 -1.523030 -11.215062
4 0.234153 -4.478066
解释:
- 生成的模拟数据包含一个自变量
和一个目标变量
。特征
是从正态分布中采样的随机变量,而目标变量
是通过一个二次方程生成的,并加入了一些噪声。
4.2 特征扩展与模型训练
接下来,我们将特征扩展为二次多项式特征,并使用线性回归模型进行训练。
# 将数据集拆分为训练集和测试集
X = X[:, np.newaxis] # 将X转化为列向量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建二次多项式特征
polynomial_features = PolynomialFeatures(degree=2)
X_train_poly = polynomial_features.fit_transform(X_train)# 使用线性回归模型训练
model = LinearRegression()
model.fit(X_train_poly, y_train)# 输出模型系数
print("模型截距 (Intercept):", model.intercept_)
print("模型系数 (Coefficients):", model.coef_)
输出:
模型截距 (Intercept): -2.6240444635236564
模型系数 (Coefficients): [ 0. -1.97702707 -2.03275601]
解释:
- 模型截距 (Intercept):表示当所有特征都为零时,目标变量的预测值。
- 模型系数 (Coefficients):系数表示每个多项式特征对目标变量的贡献。这里的一次项系数为 -1.977,二次项系数为 -2.033,模型能够捕捉到数据中的二次非线性关系。
4.3 模型预测与可视化
我们使用训练好的模型对测试集进行预测,并绘制回归曲线。
# 对测试集进行预测
X_test_poly = polynomial_features.transform(X_test)
y_pred = model.predict(X_test_poly)# 绘制原始数据点和回归曲线
plt.scatter(X, y, color='blue', label='Data Points')
plt.plot(X_test, y_pred, color='red', label='Polynomial Regression Curve')
plt.xlabel('Feature')
plt.ylabel('Target')
plt.title('Polynomial Regression')
plt.legend()
plt.show()
输出:

可视化解释:
- 数据点(蓝色):表示原始数据的分布,显示出明显的非线性趋势。
- 回归曲线(红色):模型拟合的结果,通过二次多项式回归,能够很好地捕捉到数据中的二次非线性关系。
4.4 模型评估与结果分析
我们使用均方误差(MSE)和决定系数()来评估模型的性能,并分析结果。
from sklearn.metrics import mean_squared_error, r2_score# 计算均方误差 (MSE) 和决定系数 (R²)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)print("均方误差 (MSE):", mse)
print("决定系数 (R²):", r2)
输出:
均方误差 (MSE): 8.825660578899377
决定系数 (R²): 0.9219126943457243
解释:
- 均方误差 (MSE):MSE 表示预测值与实际值之间的平均平方误差。MSE 越小,模型的预测效果越好。这里的 MSE 为 8.826,说明模型的预测误差较小。
- 决定系数 (R²):
表示模型解释了目标变量方差的百分比。这里的
为 0.922,说明模型解释了 92.2% 的目标变量方差,拟合效果较好。
4.5 不同阶数的多项式回归对比
为了更全面地理解多项式回归的影响,我们可以尝试使用不同阶数的多项式回归模型,并比较它们的表现。
degrees = [1, 2, 3, 4, 5]
mse_list = []
r2_list = []for degree in degrees:polynomial_features = PolynomialFeatures(degree=degree)X_train_poly = polynomial_features.fit_transform(X_train)X_test_poly = polynomial_features.transform(X_test)model = LinearRegression()model.fit(X_train_poly, y_train)y_pred = model.predict(X_test_poly)mse_list.append(mean_squared_error(y_test, y_pred))r2_list.append(r2_score(y_test, y_pred))# 输出不同阶数模型的MSE和R²
for degree, mse, r2 in zip(degrees, mse_list, r2_list):print(f"Degree: {degree}, MSE: {mse}, R²: {r2}")
输出:
Degree: 1, MSE: 22.834736038833358, R²: 0.7483870820958233
Degree: 2, MSE: 8.825660578899377, R²: 0.9219126943457243
Degree: 3, MSE: 8.715869441254588, R²: 0.9230105125414327
Degree: 4, MSE: 8.749054761125448, R²: 0.9226821543161257
Degree: 5, MSE: 8.909704494964572, R²: 0.9211392250804578
解释:
- 当阶数为 1 时,模型是一个简单的线性回归,无法捕捉数据中的非线性关系,因此 MSE 较大,
较低。
- 当阶数为 2 时,模型能够准确捕捉二次非线性关系,因此 MSE 最小,
最高。
- 当阶数继续增加时,MSE 和
没有显著提升,甚至略有下降,这表明过高的阶数并没有带来更好的模型表现,反而可能导致过拟合。
5. 多项式回归的优缺点及应用
5.1 优点
- 捕捉非线性关系:多项式回归能够捕捉数据中的非线性关系,并且可以通过调整多项式的阶数灵活应对不同的非线性复杂度。
- 容易实现:多项式回归建立在简单的线性回归模型之上,容易实现且计算效率高。
5.2 缺点
- 容易过拟合:当多项式的阶数过高时,模型容易过拟合训练数据,泛化能力下降。
- 特征膨胀:随着多项式阶数的增加,特征数量迅速增加,可能导致计算复杂度增加,并需要更多的内存和计算资源。
5.3 应用场景
- 非线性数据建模:在特征与目标变量之间存在明显的非线性关系时,多项式回归是一个有效的建模工具。
- 数据预处理和特征工程:多项式扩展可以作为特征工程的一部分,将原始特征转换为更复杂的特征表示,以便于捕捉复杂的模式。
6. 总结
多项式回归是一种强大的回归方法,通过对特征进行多项式扩展,它能够捕捉数据中的非线性关系。虽然多项式回归容易出现过拟合问题,但通过适当的正则化或交叉验证方法,可以有效地控制模型的复杂度。在实际应用中,多项式回归因其简洁和高效性,被广泛用于各种非线性数据的建模任务中。
相关文章:
用Python实现9大回归算法详解——04. 多项式回归算法
多项式回归 是线性回归的一种扩展,它通过将输入特征的多项式项(如平方、立方等)引入模型中,以捕捉数据中非线性的关系。虽然多项式回归属于线性模型的范畴,但它通过增加特征的多项式形式,使得模型能够拟合非…...

vue打包更新packge.json版本号
VUE项目打包自动更新版本号 此方法只针对 Vue 如果使用其他框架,可以此参照作为参考 一、先看效果 二、创建 buildVersion.js 文件 文件内容 目前只针对3位版本号 递增规则是 每次更新 加一次小版本,10次小版本向前递增一个版本。如:1.0.9 递…...

计算机视觉技术解析:从基础到前沿
第一部分:计算机视觉基础与基本原理 计算机视觉是人工智能领域的一个重要分支,旨在使计算机能够理解和处理图像和视频数据。随着深度学习技术的飞速发展,计算机视觉已经在许多实际应用场景中取得了显著的成果,如图像识别、目标检…...

unity游戏开发003:深入理解Unity中的坐标系
Unity游戏开发 “好读书,不求甚解;每有会意,便欣然忘食。” 本文目录: Unity游戏开发 Unity游戏开发深入理解Unity中的坐标系前言1. 坐标轴2. 左手坐标系3. 世界坐标系 vs. 局部坐标系4. 坐标变换5. 注意事项 总结 深入理解Unity中…...

伊索寓言两则
马和驴 马为自己精美的马具感到骄傲,在大马路上遇见了驴子子正驮着重担挪着步子,挡了路,马儿没法过去,就不耐烦叫道:真想踢你两脚,好让你走快点。驴子沉默不语,但没忘马儿的傲慢。不久后马儿患…...

嵌入式硬件产品开发:编码文件规则
目录 简介 文件内容的一般规则 文件名命名的规则 简介 一个工程是往往由多个文件组成。 这些文件怎么管理、怎么命名都是非常重要的。 文件内容的一般规则 【规则1】每个头文件和源文件的头部必须包含文件头部说明和修改记录。 源文件和头文件的头部说明必须包含的内容和次…...

设计模式 - 组合模式
💝💝💝首先,欢迎各位来到我的博客!本文深入理解设计模式原理、应用技巧、强调实战操作,提供代码示例和解决方案,适合有一定编程基础并希望提升设计能力的开发者,帮助读者快速掌握并灵活运用设计模式。 💝💝💝如有需要请大家订阅我的专栏【设计模式】哟!我会定…...
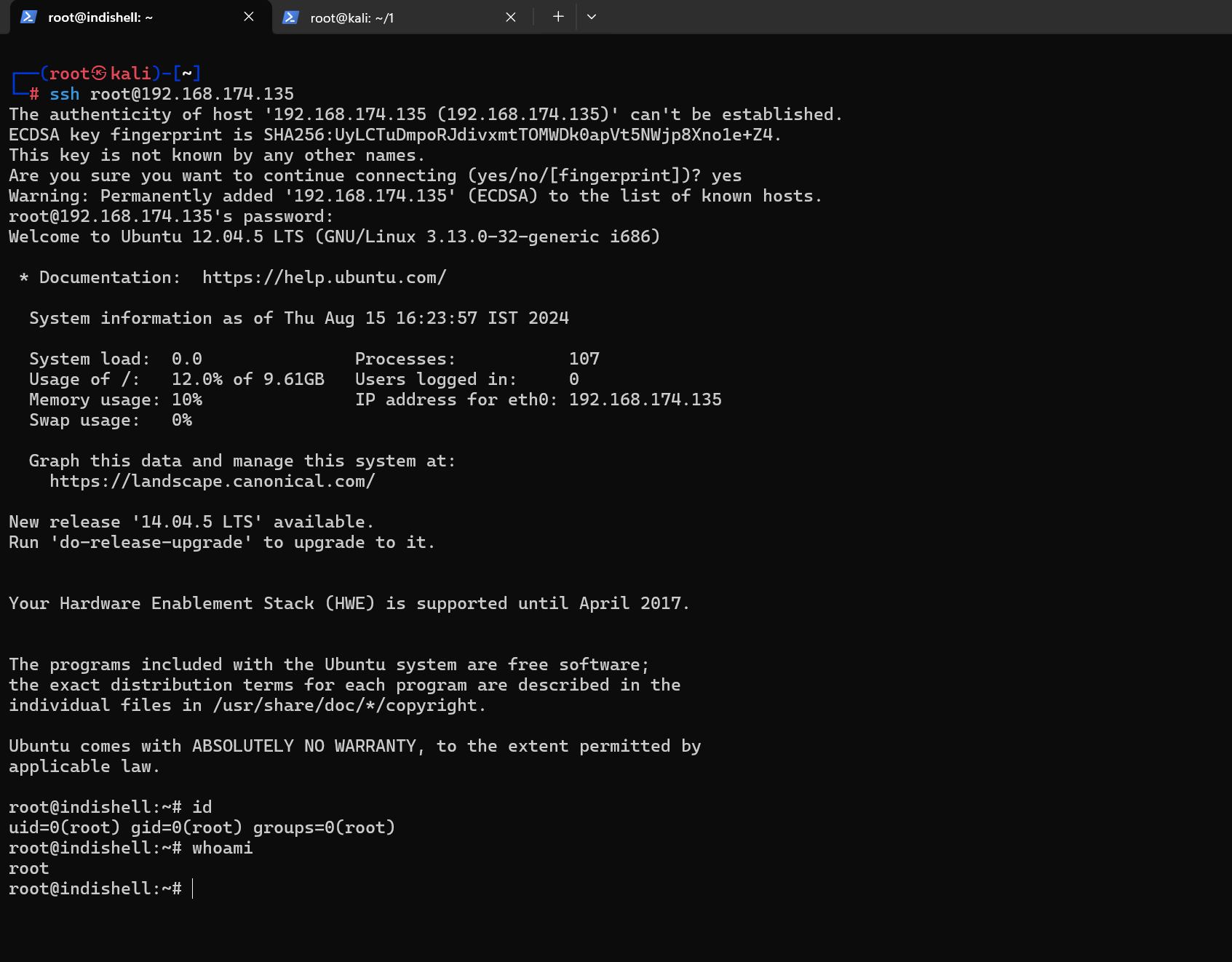
打靶记录11——Billu_b0x
靶机: https://download.vulnhub.com/billu/Billu_b0x.zip难度: 中(两种攻击路线) 目标: 取得root权限 涉及的攻击方法: 主机发现端口扫描Web信息收集SQL注入(Sqlmap跑不出来)…...

一、在cubemx上配置sd和fatfs示例演示
一、sd和fatfs的配置流程界面 1、选择sd4bits 根据自己的sd卡的硬件插槽进行选择。 2、fatfs配置由于使用的是sd卡所以直接选择sd选项 3、程序中对sd卡的初始化需要进行改动,直接使用默认的参数sd卡是挂载不上的。 4、在sd卡挂载好后,就可以使用文件系统…...

C++ 语言特性02 - 命名空间
一:概述 现代C中的命名空间是什么? C中的命名空间允许用户在命名空间范围内对类、方法、变量和函数等实体进行分组,而不是在全局范围内使用。这可以防止大型项目中的类、方法、函数和变量之间发生命名冲突。命名空间将开发人员编写的代码组织…...

drools规则引擎 规则配置文件drl语法使用案例
前提:环境搭建,参考博文springboot整合drools规则引擎 示例入门-CSDN博客案例1,商城系统消费赠送积分 100元以下, 不加分 100元-500元 加100分 500元-1000元 加500分 1000元 以上 加1000分订单pojo编写 package cn.beijing.model;import lom…...

C++编程:高性能通信组件Capnproto与Protobuf的对比分析
文章目录 0. 概要1. 测试环境2. 测试方法3. 测试结果及分析3.1 延迟测试3.2 吞吐量测试3.3 稳定性测试3.4 一对二测试记录3.5 二对一测试记录3.6 Inter-process 单个点开销分析 4. CapnProto 与 Protobuf 的对比测试总结 0. 概要 本文主要探讨了两种高性能通信组件:…...

【Python读书数据,并计算数据的相关系数、方差,均方根误差】
为了处理Python中的读书数据(假设这里指的是一系列关于书籍阅读量或评分的数据),并计算这些数据的相关系数、方差以及均方根误差(RMSE),我们首先需要明确数据的结构。这里,我将假设我们有一组关…...

垃圾收集器G1ZGC详解
G1收集器(-XX:UseG1GC) G1 (Garbage-First)是一款面向服务器的垃圾收集器,主要针对配备多颗处理器及大容量内存的机器. 以极高概率满足GC停顿时间要求的同时,还具备高吞吐量性能特征. G1将Java堆划分为多个大小相等的独立区域(Region),JVM目…...

AI芯片:高性能卷积计算中的数据复用
随着深度学习的飞速发展,对处理器的性能要求也变得越来越高,随之涌现出了很多针对神经网络加速设计的AI芯片。卷积计算是神经网络中最重要的一类计算,本文分析了高性能卷积计算中的数据复用,这是AI芯片设计中需要优化的重点之一&a…...

gitlab修改默认访问端口
GitLab 自带了一个 Nginx 服务器实例,用于处理 HTTP 和 HTTPS 请求。这个内置的 Nginx 服务器被配置为与 GitLab 应用程序实例一起工作,并且它负责处理所有前端的网络通信。 通过yum或者apt安装Gitlab时,nginx通常是被自带安装并配置好的。 …...

python——异常
Python 中的异常及继承关系 在 Python 中,异常用于表示程序在运行过程中遇到的错误,所有异常类最终都继承自 BaseException。通过异常处理,我们可以捕获和处理这些错误,避免程序崩溃。 Python 异常继承关系图 BaseException-- …...

【人工智能】利用TensorFlow.js在浏览器中实现一个基本的情感分析系统
使用TensorFlow.js在浏览器中进行情感分析是一个非常实用的应用场景。TensorFlow.js 是一个用于在JavaScript环境中训练和部署机器学习模型的库,使得开发者能够在客户端直接运行复杂的机器学习任务。对于情感分析,我们可以使用预先训练好的模型来识别文本…...

Python——扩展数据类型
Python 的扩展数据类型是对内置数据类型的增强,旨在解决特定需求,提供更高级的功能。我们来看一些常见的扩展数据类型及其原理、用途,并通过示例逐步讲解。 1. collections.namedtuple namedtuple 是增强的元组,允许用名称访问元…...

JavaScript 详解——Vue基础
第一章 JavaScript简介 为什么学习javascript ? JavaScript 是全球最流行的编程语言。 JavaScript 是属于 Web 的编程语言。 JavaScript 是 web 开发者必学的三种语言之一: HTML 定义网页的内容 CSS 规定网页的布局 JavaScript 对网页行为进行编程 …...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
