十二届蓝桥杯省赛c++(下)
1、

拿到题目一定要读懂题意,不要看到这题目就上来模拟什么闰年,一月的天数啥的。这个题目问你当天的时间,就说明年月日跟你都没关系,直接无视就好了。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>using namespace std;#define ll long long//能开long long就开,避免爆数据 int main()
{ll n;cin >> n;n /= 1000;//先把毫秒转化为秒 ll hour = (n / 60 / 60) % 24;//求出小时数,一定要记得取模 ll minute = (n % 3600 / 60) % 60;//分钟数 ll s = n % 3600 % 60;//秒数 if (hour < 10) cout << 0;//记得处理好零的输出 cout << hour << ':';if (minute < 10) cout << 0;cout << minute << ':';if (s < 10) cout << 0;cout << s;return 0;
}2、
(1)动态规划:
闫氏dp分析法:
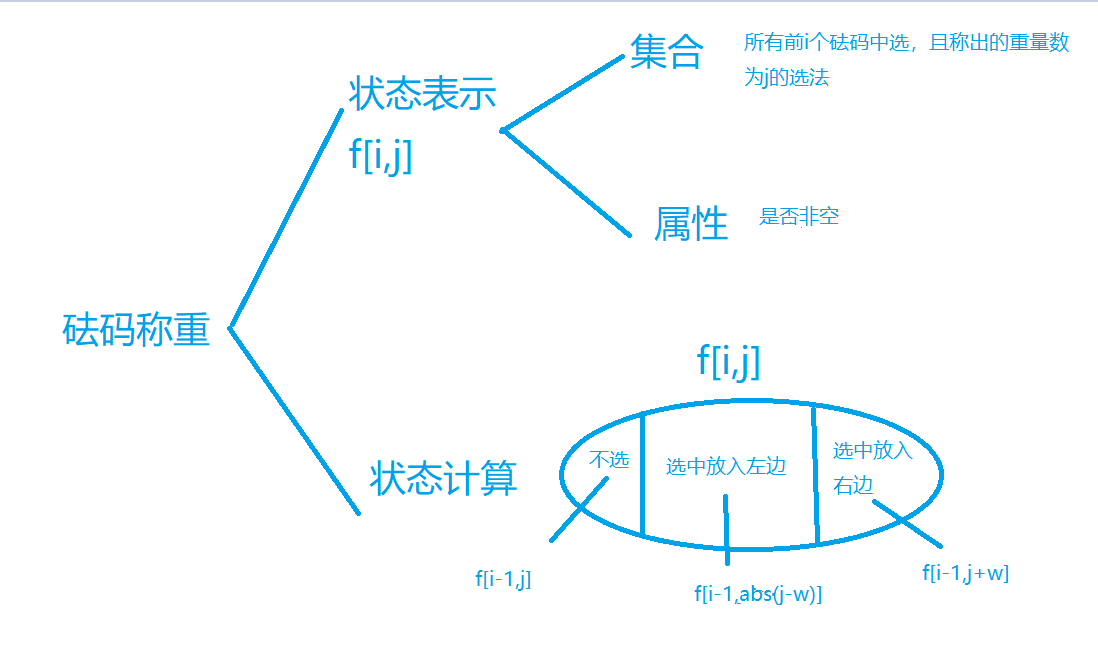
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>using namespace std;#define N 1010000int f[150][N] ,n ,w[N] ,ans ,sum; int main()
{cin >> n;for (int i = 1 ;i <= n ;i ++) cin >> w[i] ,sum += w[i];//拿sum存储砝码的重量之和 f[0][0] = 1;//初始化,零个砝码测出质量为0的方案有一个 for (int i = 1 ;i <= n ;i ++){for (int j = 0 ;j <= sum ;j ++){f[i][j] = f[i - 1][j];//第i个砝码没有用 f[i][j] += f[i - 1][abs(j - w[i])];//第i个砝码放左边 f[i][j] += f[i - 1][j + w[i]];//第i个砝码放右边 }}for (int i = 1 ;i <= sum ;i ++)if (f[n][i]) ans ++;//如果有值,说明前n个砝码可以测出来重量为i的物品,答案加一 cout << ans;return 0;
}(2)dfs暴力,拿一半分
如果这道题实在没时间做或者说想不到思路,那么我们就可以考虑暴力拿分
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>using namespace std;#define N 1010000int n ,w[N] ,ans;
bool vis[N];void dfs(int k ,int g)
{if (k > n){if (g > 0 && !vis[g]){ans ++;vis[g] = true;}return;}dfs(k + 1 ,g);dfs(k + 1 ,g + w[k]);dfs(k + 1 ,abs(g - w[k]));
}int main()
{cin >> n;for (int i = 1 ;i <= n ;i ++){cin >> w[i];}dfs(0 ,0);cout << ans; return 0;
}3、
这一届的题目从这一题开始往后,难度就起来了。
1、先说暴力做法吧,可以拿四十分,直接预处理一千行
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;const int N = 1e3 + 10;int n = 1000;
int a[N][N];int main() {a[1][1] = 1;for (int i = 2; i <= n; i ++) // 预处理for (int j = 1; j <= i; j ++)a[i][j] = a[i - 1][j] + a[i - 1][j - 1];int x; cin >> x;int cnt = 0;for (int i = 1; i <= n; i ++) // 枚举for (int j = 1; j <= i; j ++) {cnt ++;if (a[i][j] == x) {cout << cnt;return 0;}} return 0;
}
2、正解
关于这道题我们需要明白:杨辉三角其实就是组合数!如图:
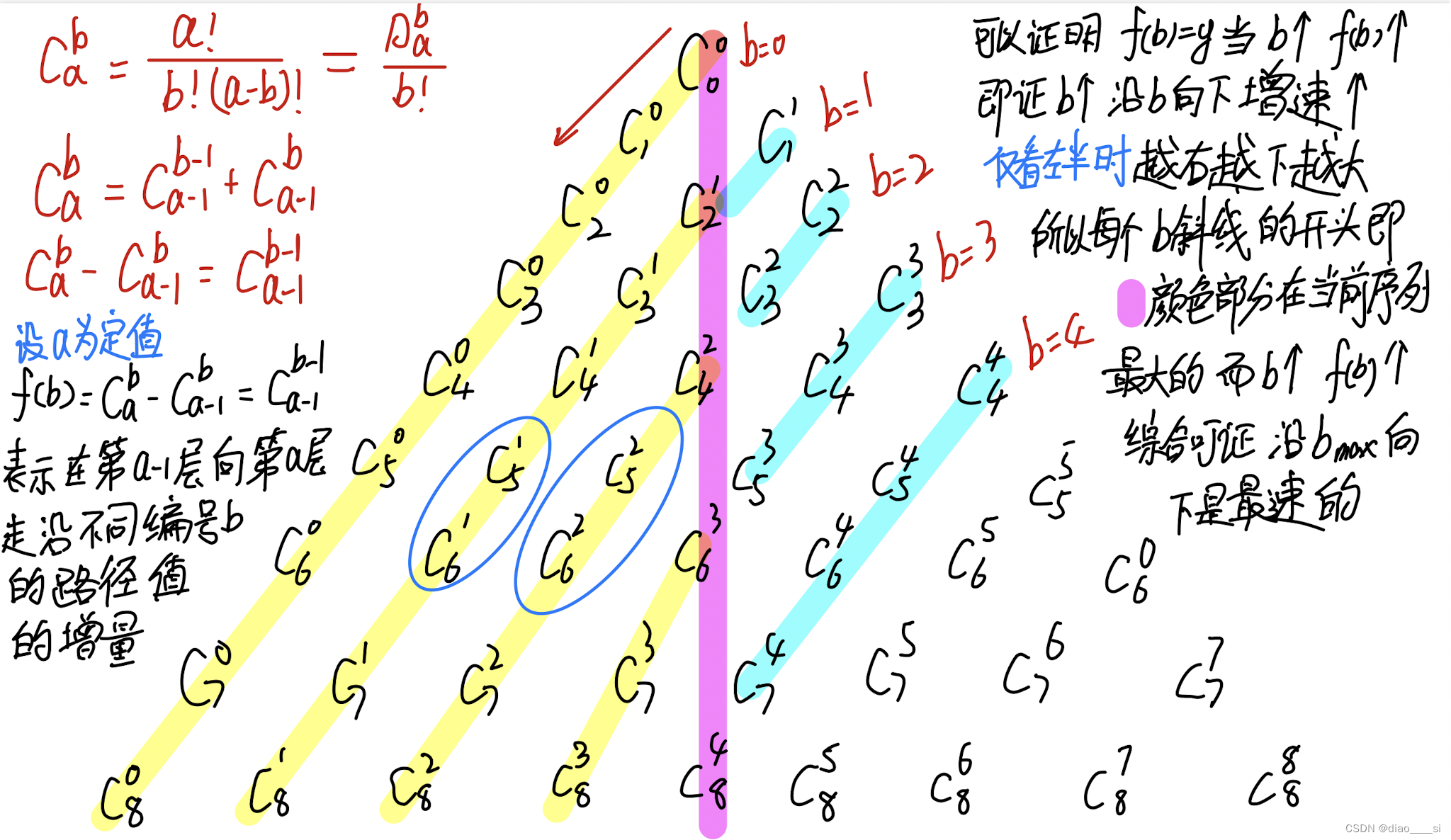
从图中我们可以观察出两个性质:
1、以中间的紫色分割线为界,左右两边的数值是相等的。那么右边存在的某一个值左边一定也存在,并且根据题目的排序方式来看左边相对而言更加靠前,也就是说某一个数N第一次一定是在左边先出现。因此,我们要找的结果一定是在左边部分中。
2、中间一列数从上往下是在递增的,每一横排从左往右也在递增,每一斜行从上往下也在递增。所以每个斜行都保持了单调性。
现在知道了这两个性质,我们可以想想怎么从左边中找到N。直接枚举的复杂度太高,不可取,而根据第二条中所提到的单调性,我们可以很自然的想到二分法。那么该如何二分?竖着?横着?这都不可取,因为不论是哪一种我们都无从下手。所以我们需要斜着来!每一个斜行从紫色部分开始,也就是C(k,2*k)的形式,到C(k ,n)结束(为什么从n结束?可以思考一下,倘若想不明白可以私信问我)。由于n最大1e9,C(34, 17) > 1e9, C(32, 16) < 1e9,因此只要枚举前16个斜行即可。
C(k, r)对应的顺序值为:(r + 1) * r / 2 + k + 1
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>using namespace std;#define ll long longll n;ll c(int a ,int b)
{ll res = 1;for (int i = a ,j = 1 ;j <= b ;i -- ,j ++)//求组合数的过程 {res = res * i / j;if (res > n) return res;//如果res已经大于n就不用在求了,肯定不是答案,直接返回。这样也可以避免爆数据 }return res;
}bool h(int k)
{int l = 2 * k ,r = n;while (l < r){ll mid = (l + r) / 2;if (c(mid ,k) >= n) r = mid;elsel = mid + 1;}if (c(l ,k) != n) return false;cout << 1ll * (l + 1) * l / 2 + k + 1;//如果找到了,输出位置 return true;
}int main()
{cin >> n;for (int i = 16 ; ;i --)//枚举前十六个斜行 if (h(i)) break;return 0;
}
4、
我也不会。。。
5、
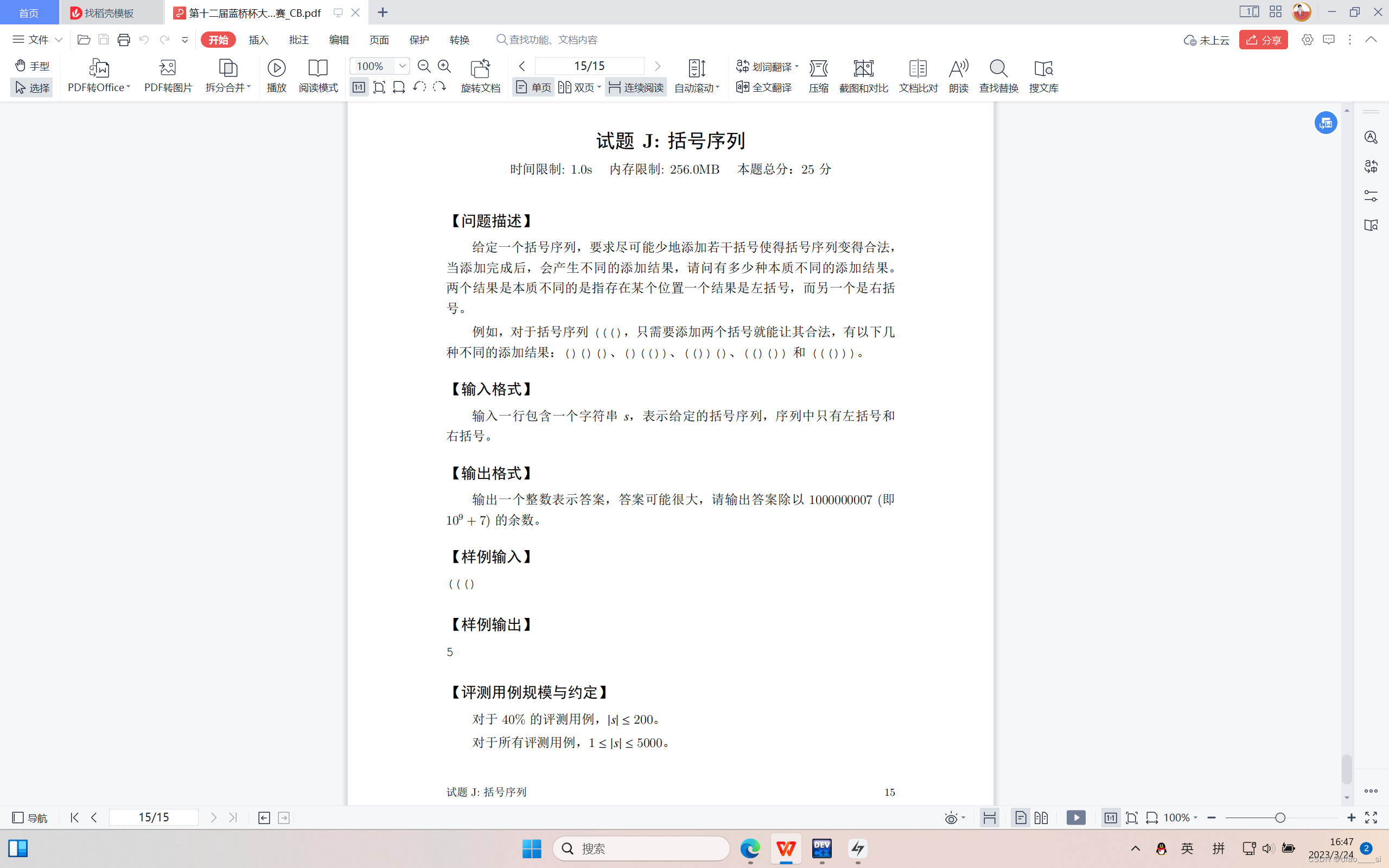
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>using namespace std;#define ll long long
#define N 5500const int mod = 1000000007;ll f[N][N] ,len;
char s[N];ll hu()
{memset(f ,0 ,sizeof(f));f[0][0] = 1;for (int i = 1 ;i <= len ;i ++){if (s[i] == '('){for (int j = 1 ;j <= len ;j ++)f[i][j] = f[i - 1][j - 1];}else {f[i][0] = (f[i - 1][0] + f[i - 1][1]) % mod;for (int j = 1 ;j <= len ;j ++)f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % mod;}}for (int i = 0 ;i <= len ;i ++)if (f[len][i]) return f[len][i];return -1;}int main()
{scanf("%s" ,s + 1);len = strlen(s + 1);ll l = hu();reverse(s + 1 ,s + len + 1);for (int i = 1 ;i <= len ; i ++){if (s[i] == '(') s[i] = ')';elses[i] = '(';}ll r = hu();printf("%lld" ,l * r % mod);return 0;
}
相关文章:

十二届蓝桥杯省赛c++(下)
1、 拿到题目一定要读懂题意,不要看到这题目就上来模拟什么闰年,一月的天数啥的。这个题目问你当天的时间,就说明年月日跟你都没关系,直接无视就好了。 #include <iostream> #include <cstring> #include <algori…...
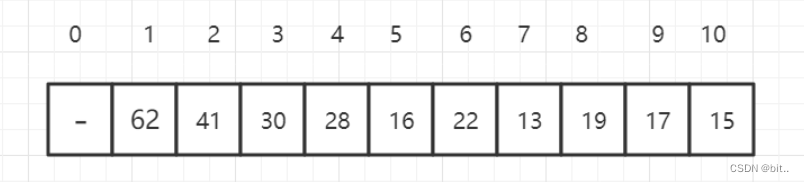
数据结构与算法——堆的基本存储
目录 一、概念及其介绍 二、适用说明 三、结构图示 四、Java 实例代码 五.堆和栈的区别 一、概念及其介绍 堆(Heap)是计算机科学中一类特殊的数据结构的统称。 堆通常是一个可以被看做一棵完全二叉树的数组对象。 堆满足下列性质: 堆中某个节点的值总是不大…...

来了来了 !!!K8s指令、yaml部署
文章目录k8s资源清单一、k8s资源指令1、基础操作2、命令手册二、资源清单1、required2、optional3、other4、资源清单格式5、常用命令三、部署实例1、nginx3、eureka部署k8s资源清单 一、k8s资源指令 1、基础操作 #创建且运行一个pod #deployment、rs、pod被自动创建 kubect…...

spring-cloud-feign实战笔记
feign 配置 针对单个feign接口进行配置feign:client:config:# feignName 注意这里与contextId一致,不能写成name(FeignClientFactoryBean#configureFeign)# 不能写成 client-b (微服务名称),否则不生效helloFeignClient: # conte…...

【Pytorch】利用PyTorch实现图像识别
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052 这是目录使用torchvision库的datasets类加载常用的数据集或自定义数据集使用torchvision库进行数据增强和变换,自定义自己的图像分类数据集并使用torchvision库加载它们使…...

在家查找下载最新《柳叶刀》The Lancet期刊文献的方法
《柳叶刀》The Lancet简介: 《柳叶刀》The Lancet是全球顶尖综合性医学期刊,每周都会发表来自世界各地顶尖科学家的研究精粹。是由托马斯威克利(Thomas Wakley)创办于1823年,由爱思唯尔(Elsevierÿ…...
当下的网络安全行业前景到底怎么样?还能否入行?
前言网络安全现在是朝阳行业,缺口是很大。不过网络安全行业就是需要技术很多的人达不到企业要求才导致人才缺口大常听到很多人不知道学习网络安全能做什么,发展前景好吗?今天我就在这里给大家介绍一下。网络安全作为目前比较火的朝阳行业&…...

SpringCloud:SpringAMQP介绍
Spring AMQP是基于RabbitMQ封装的一套模板,并且还利用SpringBoot对其实现了自动装配,使用起来非常方便。Spring AMQP官方地址 Spring AMQP提供了三个功能: 自动声明队列、交换机及其绑定关系基于注解的监听器模式,异步接收消息封…...

第十三届蓝桥杯省赛 python B组复盘
文章目录前言主要内容🦞试题 A:排列字母思路代码🦞试题 B:寻找整数思路代码🦞试题 C:纸张尺寸思路代码🦞试题 D:数位排序思路代码🦞试题 E:蜂巢思路代码&…...
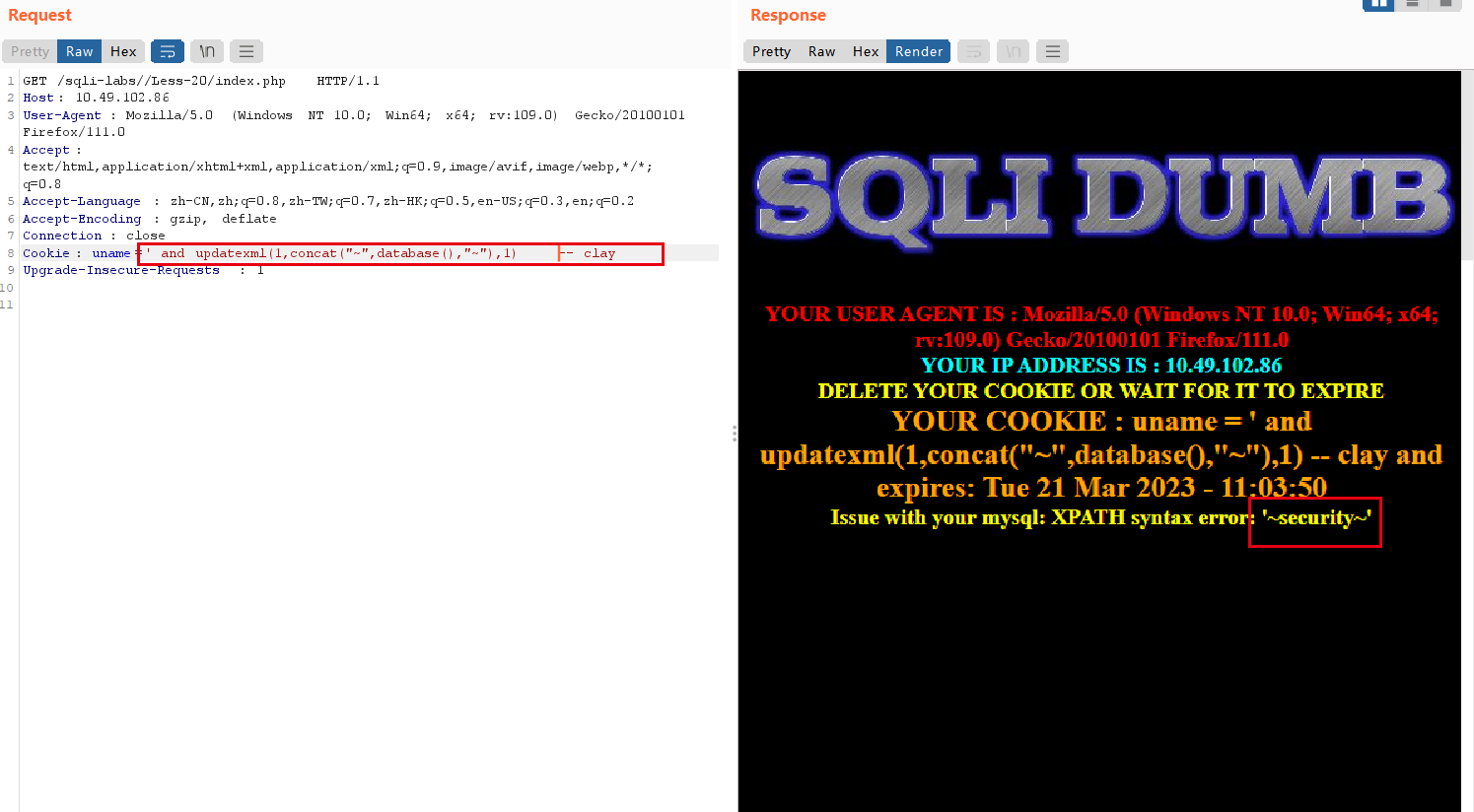
SQL注入之HTTP请求头注入
Ps: 先做实验,在有操作的基础上理解原理会更清晰更深入。 一、实验 sqli-lab 1. User-Agent注入 特点:登陆后返回用户的 User-Agent --> 服务器端可能记录用户User-Agent 输入不合法数据报错 payload: and updatexml(1,concat("~&…...

Metasploit详细教程
第一步:安装和启动Metasploit 您可以从Metasploit官方网站下载适用于您操作系统的Metasploit框架。安装Metasploit框架后,您可以使用以下命令来启动Metasploit: msfconsole该命令将启动Metasploit控制台。 第二步:查找目标设备…...

【ChatGPT】Notion AI 从注册到体验:如何免费使用
欢迎关注【youcans的GPT学习笔记】原创作品,火热更新中 【ChatGPT】Notion AI 从注册到体验1. Notion AI 介绍1.1 Notion AI 简介1.2 Notion AI 的核心能力1.3 Notion AI 与 ChatGPT 的比较2. Notion AI 国内用户注册2.1 PC 端用户注册2.2 移动端用户注册3. Notion …...
每个开发人员都需要掌握的10 个基本 SQL 命令
SQL 是一种非常常见但功能强大的工具,它可以帮助从任何数据库中提取、转换和加载数据。数据查询的本质在于SQL。随着公司和组织发现自己处理的数据量迅速增加,开发人员越来越需要有效地使用数据库来处理这些数据。所以想要暗恋数据领域,SQL是…...

Vue项目预渲染
前言 Ajax 技术的出现,让我们的 Web 应用能够在不刷新的状态下显示不同页面的内容,这就是单页应用。在一个单页应用中,往往只有一个 html 文件,然后根据访问的 url 来匹配对应的路由脚本,动态地渲染页面内容。单页应用…...

可别再用BeanUtils了(性能拉胯),试试这款转换神器
老铁们是不是经常为写一些实体转换的原始代码感到头疼,尤其是实体字段特别多的时候。有的人会说,我直接使用get/set方法。没错,get/set方法的确可以解决,而且也是性能较高的处理方法,但是大家有没有想过,要…...

Transformer 杂记
Transformer输入的是token,来自语言序列的启发。卷积神经网络(CNN)是如何进行物种分类的.它实际是直接对特征进行识别,也就是卷积神经网络最基本的作用:提取图像的特征。例如:卷积神经网络判断一只狗的时候,…...

实现异步的8种方式
前言异步执行对于开发者来说并不陌生,在实际的开发过程中,很多场景多会使用到异步,相比同步执行,异步可以大大缩短请求链路耗时时间,比如:「发送短信、邮件、异步更新等」,这些都是典型的可以通…...
Github隐藏功能显示自己的README,个人化你的Github主页
Github隐藏功能:显示自己的README 你可能还不知道,GitHub 悄悄上线了一个全新的个人页功能,显示一个自定义的 README.MD 在个人首页。要激活此功能,需要新建一个与自己 ID 同名的 Repository,新 Repo 里的README.MD将…...
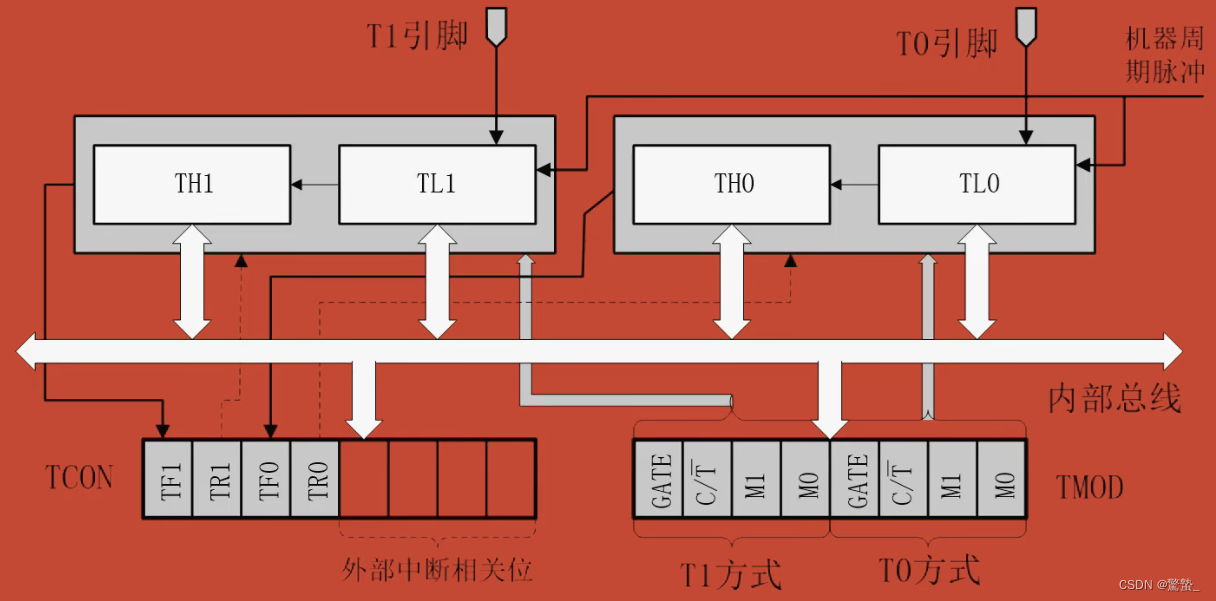
单片机 | 51单片机原理
【金善愚】 单片机应用原理篇 笔记整理 课程视频 :https://space.bilibili.com/483942191/channel/collectiondetail?sid51090 文章目录一、引脚分布介绍1.分类2.电源引脚3.时钟引脚(2根)4.控制引脚(4根)5.端口引脚(32根)二、存储器结构及空间分布介绍1.存储器的划…...
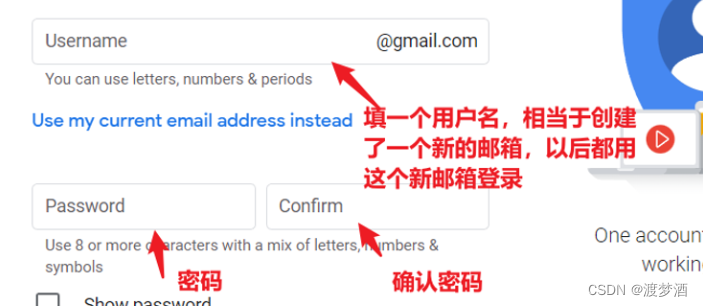
(只需五步)注册谷歌账号详细步骤,解决“此电话号码无法验证”问题
目录 第一步:打开google浏览器 第二步:设置语言为英语(美国) 第三步:点击重新启动,重启浏览器 第四步:开始注册 第五步,成功登录google账号! 如果出现这样的原因&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
