虹软科技25届校招笔试算法 A卷

目录
- 1. 第一题
- 2. 第二题
- 3. 论述题
⏰ 时间:2024/08/18
🔄 输入输出:ACM格式
⏳ 时长:2h
本试卷分为不定项选择,编程题,必做论述题和选做论述题,这里只展示编程题和必做论述题,一共三道。
注意,虹软的笔试题目表述的不太清晰,并且也没有给出数据范围,这里针对表述做了一些优化。
1. 第一题
已知字符串 S S S 只包含 A , B A,B A,B 两种字符,设 X X X 为 S S S 中所有 A A A 的索引的集合, Y Y Y 为 S S S 中所有 B B B 的索引的集合。若 S S S 满足以下条件,则称 S S S 为有序字符串。
- X X X 与 Y Y Y 之间存在双射 f f f,满足 ∀ i ∈ X , f ( i ) > i \forall i\in X, f(i)>i ∀i∈X,f(i)>i。
给定有序字符串 S S S,按照下述规则计算 S S S 的分数,设 P , Q P,Q P,Q 分别为有序字符串
- A B AB AB 的分数 = 1 =1 =1
- P Q PQ PQ 的分数 = = = P P P 的分数 + + + Q Q Q 的分数
- A P B APB APB 的分数 = = = 2 ⋅ P 2\cdot P 2⋅P 的分数
输入描述
输入一个仅包含 A , B A,B A,B 的字符串
输出描述
输出一个整数
题解
这道题本来就有些绕,再加上原本的表述不够清晰,所以很容易误解题意,博主这里稍微修改了下表述。
首先来看什么是有序字符串?这里举一个例子。设 S = A A B A A B B B S=AABAABBB S=AABAABBB ,从而 X = { 0 , 1 , 3 , 4 } , Y = { 2 , 5 , 6 , 7 } X=\{0,1,3,4\},\,Y=\{2,5,6,7\} X={0,1,3,4},Y={2,5,6,7}。我们可以找到一个双射
0 → 2 1 → 5 3 → 6 4 → 7 0\to2\\ 1\to 5 \\ 3\to6\\ 4\to 7 0→21→53→64→7
在这个映射下, 2 > 0 , 5 > 1 , 6 > 3 , 7 > 4 2>0,5>1,6>3,7>4 2>0,5>1,6>3,7>4,因此 S S S 是有序的。更通俗地来讲,对于 S S S 中的每一个 A A A,我们都要在 S S S 中找到一个与之配对的 B B B,使得 B B B 的索引大于 A A A 的索引,这样的 S S S 才是有序字符串。
由于双射的性质,易知 ∣ X ∣ = ∣ Y ∣ |X|=|Y| ∣X∣=∣Y∣,因此如果 S S S 是有序的,那么它的长度一定是偶数。此外,一定有 S [ 0 ] = A , S [ − 1 ] = B S[0]=A,\,S[-1]=B S[0]=A,S[−1]=B,即 S S S 的首字符一定是 A A A,尾字符一定是 B B B,若不然,假设 S [ 0 ] = B S[0]=B S[0]=B,我们无法在 S S S 中找到与它配对的 A A A,使得 A A A 的下标小于它,对于 S [ − 1 ] S[-1] S[−1] 同理。设 S S S 的长度为 2 n , n = 1 , 2 , ⋯ 2n,\;n=1,2,\cdots 2n,n=1,2,⋯,易知 n = 1 n=1 n=1 时 S = A B S=AB S=AB,我们称这样的 S S S 为基本串(自己瞎起的名hh,方便后面讲)。
现在回到一般情况,设 S S S 的长度为 2 n 2n 2n, X = { a 1 , a 2 , ⋯ , a n } , Y = { b 1 , b 2 , ⋯ , b n } X=\{a_1,a_2,\cdots,a_n\},\,Y=\{b_1,b_2,\cdots,b_n\} X={a1,a2,⋯,an},Y={b1,b2,⋯,bn}。假设 X , Y X,Y X,Y 均是从左向右统计出来的,从而 X , Y X,Y X,Y 均是有序数组。容易得出以下结论:
S 是有序字符串 ⇔ ∀ i , a i < b i S 是有序字符串 \Leftrightarrow \forall i,\,a_i<b_i S是有序字符串⇔∀i,ai<bi
充分性显然,必要性用反证法证明。
从题中所给的信息,可以猜测,以下两个事件为对立事件(博主还没有来得及证明,欢迎大家在评论区补充):
- S S S 可以拆成两个有序字符串 P , Q P,Q P,Q,即 S = P Q S=PQ S=PQ。且拆法不会影响到 S S S 的分数。
- S S S 可以拆成 A P B APB APB 的形式,其中 P P P 是有序的。
很明显可以用递归来做,每次判断当前的 S S S 属于以上哪一种情况,然后递归进行求解, A B AB AB 的分数为 1 1 1 可以作为递归终止条件。
以 S = A A B A A B B B S=AABAABBB S=AABAABBB 为例。显然 S S S 不能拆成两个有序字符串,因此将其表示成 A P B APB APB 的形式,其中 P = A B A A B B P=ABAABB P=ABAABB 是一定是有序字符串。如果将 P P P 拆成 A R B ARB ARB 的形式,由于 R = B A A B R=BAAB R=BAAB 不是有序的,根据之前的猜想, P P P 一定可以拆成两个有序字符串 U , V U,V U,V,且拆法不会影响到最终分数。很明显 U = A B , V = A A B B U=AB,V=AABB U=AB,V=AABB。于是可以计算 S S S 的分数: S = 2 P = 2 ( U + V ) = 2 ( 1 + 2 ) = 6 S=2P=2(U+V)=2(1+2)=6 S=2P=2(U+V)=2(1+2)=6。
#include <bits/stdc++.h>using namespace std;bool is_ordered(const string& s, int l, int r) {vector<int> a_indices, b_indices;for (int i = l; i < r + 1; i++) {if (s[i] == 'A') a_indices.push_back(i);else b_indices.push_back(i);}if (a_indices.size() != b_indices.size()) return false;for (int i = 0; i < a_indices.size(); i++) {if (a_indices[i] > b_indices[i]) return false;}return true;
}// 计算有序字符串s在闭区间[l, r]上的分数
int score(const string& s, int l, int r) {// 基本串情形if (r - l == 1 && s.substr(l, 2) == "AB") return 1;// 看一下成否拆成PQ,分成[l, i], [i + 1, r]for (int i = l; i < r; i++) {if (is_ordered(s, l, i) && is_ordered(s, i + 1, r)) {// 拆法不会影响分数,直接返回即可return score(s, l, i) + score(s, i + 1, r);}}// 因为是对立事件,所以直接返回return 2 * score(s, l + 1, r - 1);
}int main() {string s;cin >> s;int ans = score(s, 0, s.size() - 1);cout << ans << endl;return 0;
}
后续证明了猜想会在这里补充,也欢迎广大网友补充。
2. 第二题
有红、绿、蓝三种颜色(分别用R、G、B表示)的小球,其数量分别为 a , b , c a,b,c a,b,c。现在想将这些小球排成一列,但不希望相邻的两个小球出现相同颜色,请问有多少种排列方法?
输入描述
第一行为 a 、 b 、 c a、b、c a、b、c 对应的三个数字,以空格隔开
输出描述
输出为排列方法的总数
题解
本题较为简单,dfs即可,从左到右枚举并记录上一次放的什么颜色。
#include <bits/stdc++.h>using namespace std;int dfs(int a, int b, int c, int last) {if (a == 0 && b == 0 && c == 0) return 1;int ans = 0;if (last != 0 && a > 0) {ans += dfs(a - 1, b, c, 0); // 选择红色}if (last != 1 && b > 0) {ans += dfs(a, b - 1, c, 1); // 选择绿色}if (last != 2 && c > 0) {ans += dfs(a, b, c - 1, 2); // 选择蓝色}return ans;
}int main() {int a, b, c;cin >> a >> b >> c;cout << dfs(a, b, c, -1) << endl;return 0;
}
其中 dfs(a, b, c, last) 表示红球有 a a a 个,绿球有 b b b 个,蓝球有 c c c 个,且上一次放置的是 last 颜色的情况下,能够放置的方法总数。初始时没有放置,故 last == -1。
考虑边界条件。例如只有一个红球的情况下,此时放置方案只有一种,因此
1 = d f s ( 1 , 0 , 0 , − 1 ) = d f s ( 0 , 0 , 0 , 0 ) 1=dfs(1,0,0,-1)=dfs(0,0,0,0) 1=dfs(1,0,0,−1)=dfs(0,0,0,0)
故可知边界条件 d f s ( 0 , 0 , 0 , l a s t ) = 1 dfs(0,0,0,last)=1 dfs(0,0,0,last)=1。
3. 论述题
假设有一张宽为 M M M,高为 N N N 的黑白图像,每个元素都是 0 0 0 或 1 1 1,其中 0 0 0 表示黑色像素, 1 1 1 表示白色像素,要在该图像中找到一个宽为 W W W,高为 H H H 的矩形子区域( W < M , H < N W<M,H<N W<M,H<N 且已知),使得该区域内的白色像素数最多,并计算该区域内的白色像素数。
注意 O ( M N H W ) O(MNHW) O(MNHW) 的实现不计分,请用文字描述或者伪代码说明算法过程,并分析时间复杂度。
题解
容易知道枚举所有子矩形的时间复杂度为 O ( ( M − W + 1 ) ⋅ ( N − H + 1 ) ) O((M-W+1)\cdot(N-H+1)) O((M−W+1)⋅(N−H+1))。
计算子矩形中的白色像素数等价于计算子矩形中的所有元素和。
如果暴力求解的话,即每次枚举的时候都计算一遍元素和,那么总时间复杂度为 O ( W H ⋅ ( M − W + 1 ) ⋅ ( N − H + 1 ) ) = O ( W H M N ) O(WH\cdot(M-W+1)\cdot(N-H+1))=O(WHMN) O(WH⋅(M−W+1)⋅(N−H+1))=O(WHMN),不符合题意。
求区域的元素和可以使用「二维前缀和」算法,我们可以在 O ( M N ) O(MN) O(MN) 的时间内预处理出一个前缀和数组,然后每次枚举的时候只需要在 O ( 1 ) O(1) O(1) 的时间内就能算出子矩形的所有元素和,此时总时间复杂度为
O ( M N + ( M − W + 1 ) ⋅ ( N − H + 1 ) ) O(MN+(M-W+1)\cdot(N-H+1)) O(MN+(M−W+1)⋅(N−H+1))
相关文章:

虹软科技25届校招笔试算法 A卷
目录 1. 第一题2. 第二题3. 论述题 ⏰ 时间:2024/08/18 🔄 输入输出:ACM格式 ⏳ 时长:2h 本试卷分为不定项选择,编程题,必做论述题和选做论述题,这里只展示编程题和必做论述题,一共三…...

C++ | Leetcode C++题解之第345题反转字符串中的元音字母
题目: 题解: class Solution { public:string reverseVowels(string s) {auto isVowel [vowels "aeiouAEIOU"s](char ch) {return vowels.find(ch) ! string::npos;};int n s.size();int i 0, j n - 1;while (i < j) {while (i < …...
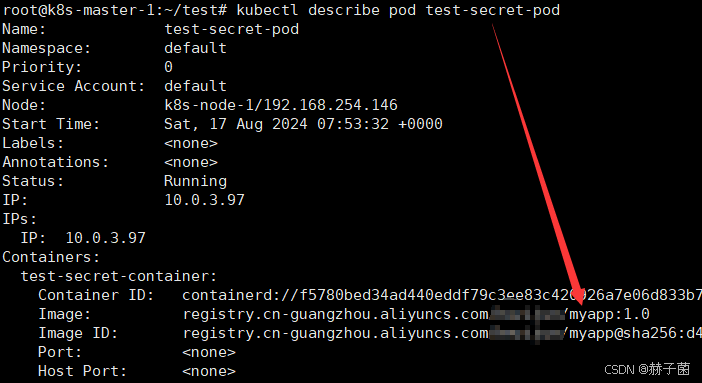
Kubernetes拉取阿里云的私人镜像
前提条件 登录到阿里云控制台 拥有阿里云的ACR服务 创建一个命名空间 获取仓库的访问凭证(可以设置固定密码) 例如 sudo docker login --usernameyourAliyunAccount registry.cn-guangzhou.aliyuncs.com 在K8s集群中创建一个secret 使用kubectl命令行…...
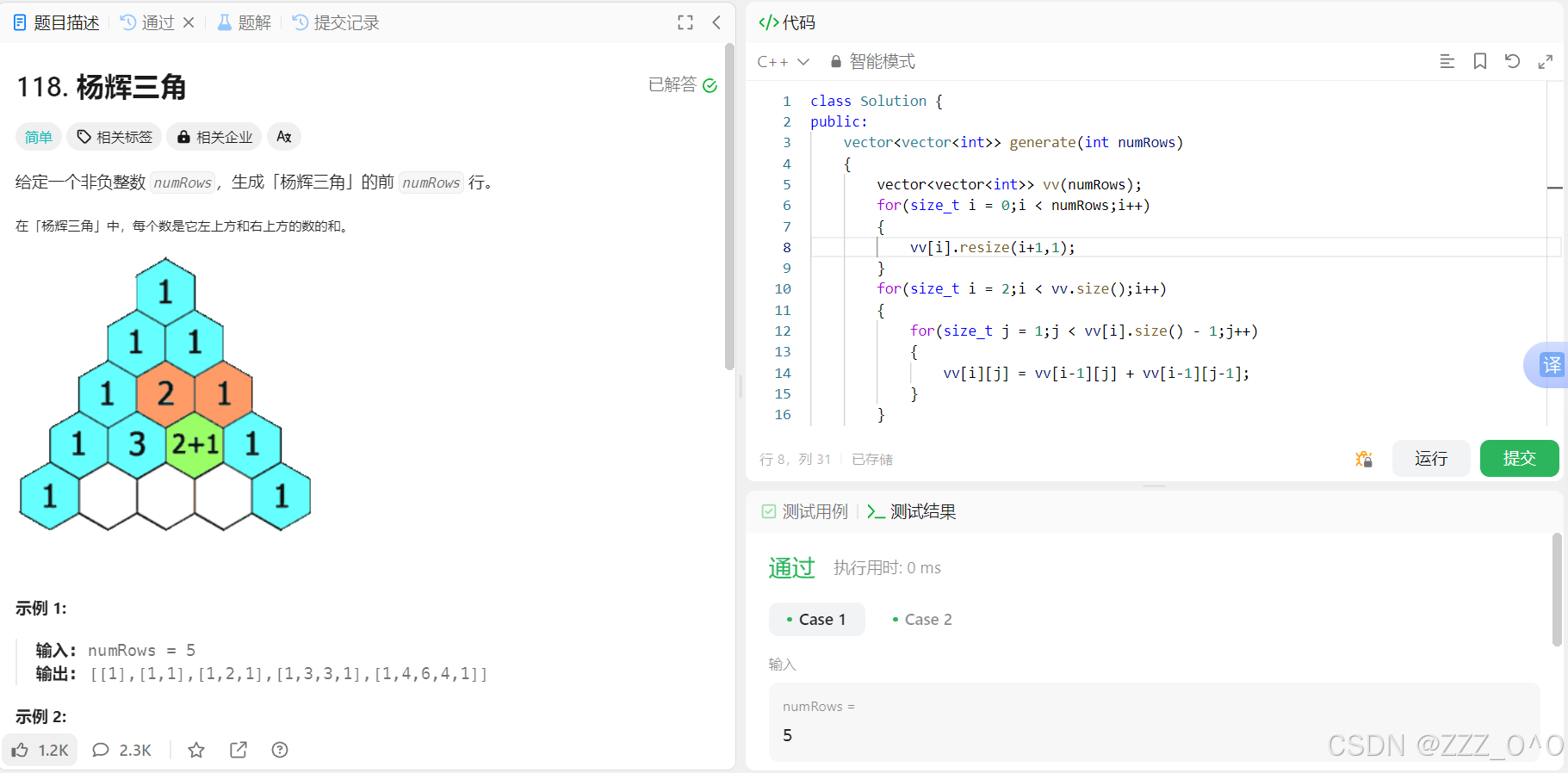
Leetcode每日刷题之118.杨辉三角
1.题目解析 杨辉三角作为一个经典的数学模型,其基本原理相信大家已经耳熟能详,这里主要是在学习了vector之后,对于本题有了新的解法,更加简便。关于vector的基本使用详见 面向对象程序设计(C)之 vector(初阶࿰…...

【ARM 芯片 安全与攻击 5.2 -- 芯片中侧信道攻击与防御方法介绍】
文章目录 什么是 Speculation Barriers?如何使用 Speculation Barriers?什么是 PAN?如何启用 PAN?使用 PAN 保护操作系统Spectre 攻击防御示例Meltdown 攻击防御示例Summary什么是 Speculation Barriers? Speculation Barriers,是一种防止处理器在投机执行中泄漏敏感信息…...
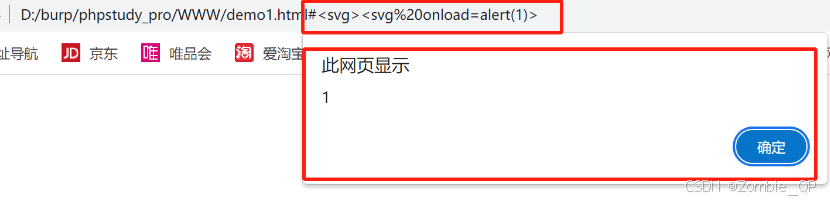
XSS-games
XSS 1.XSS 漏洞简介2.XSS的原理3.XSS的攻击方式4.XSS-GAMESMa SpaghetJefffUgandan KnucklesRicardo MilosAh Thats HawtLigmaMafiaOk, BoomerWW3svg 1.XSS 漏洞简介 XSS又叫CSS(Cross Site Script)跨站脚本攻击是指恶意攻击者往Web页面里插入恶意Sc…...
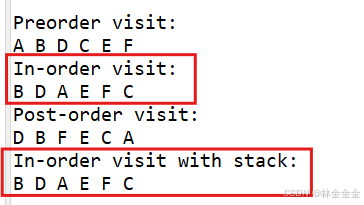
日撸Java三百行(day25:栈实现二叉树深度遍历之中序遍历)
目录 一、栈实现二叉树遍历的可行性 二、由递归推出栈如何实现中序遍历 1.左子树入栈 2.根结点出栈 3.右子树入栈 4.实例说明 三、代码实现 总结 一、栈实现二叉树遍历的可行性 在日撸Java三百行(day16:递归)中,我们讲过…...
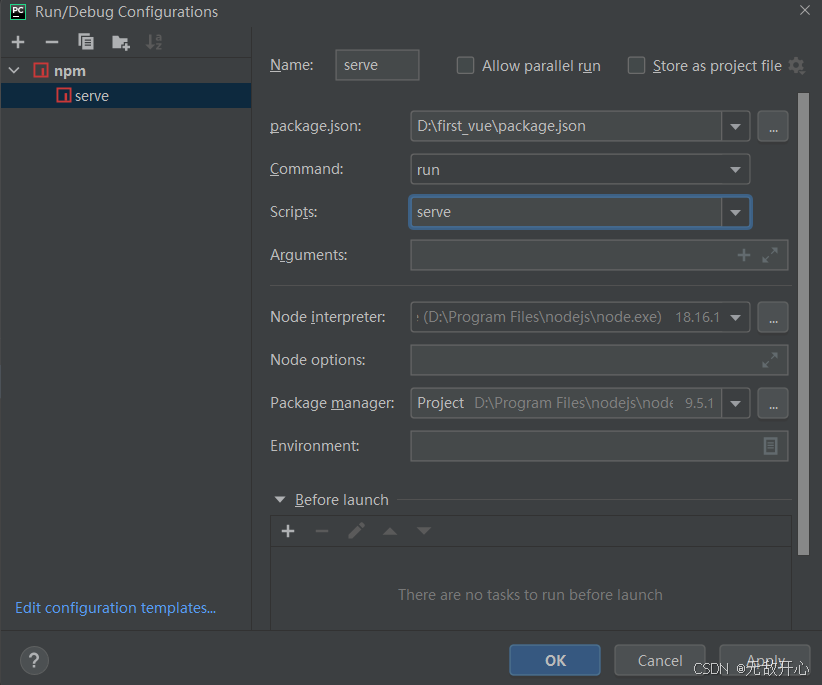
【vue讲解:ref属性、动态组件、插槽、vue-cli创建项目、vue项目目录介绍、vue项目开发规范、es6导入导出语法】
0 ref属性(组件间通信) # 1 ref属性放在普通标签上<input type"text" v-model"name" ref"myinput">通过 this.$refs[myinput] 拿到的是 原生dom对象操作dom对象:改值,换属性。。。# 2 ref属…...

ubuntu:最新安装使用docker
前言 系统:ubuntu 22.04 desktop 目的:安装使用docker 安装小猫猫 没有安装包的,可以自己去瞅瞅,这里不提供下载方式 sudo dpkg -i ./cat-verge_1.7.5_amd64.deb 在应用里,打开这个软件,并开启系统猫猫 配…...

Linux ssh 免密失效
sudo chmod -R 777 /home/xxx sudo chown -R xxx:xxx /home/xxx 为什么我输入这两条指令后,ssh免密失效了? 当你使用 sudo chmod -R 777 /home/xxx 和 sudo chown -R xxx:xxx /home/xxx 这两条指令后,可能会导致 SSH 免密登录失效的原因有以…...

k8s上部署ingress-controller
一、安装helm仓库 # helm pull ingress-nginx/ingress-nginx 二、修改 三、运行 # kubectl label nodes node01.110111.cn ingresstrue# kubectl label nodes node02.110112.cn ingresstrue# helm upgrade --install ingress-nginx -n ingress-nginx . -f values.yaml 四、检…...
)
Android 13 about launcher3 (1)
Android 13 Launcher3 android13#launcher3#分屏相关 Launcher3修改 wm density界面布局不改变 /packages/apps/Launcher3/src/com/android/launcher3/InvariantDeviceProfile.java Launcher的默认配置加载类,通过InvariantDeviceProfile方法可以看出,…...

服务器数据恢复—raid5阵列热备盘未全部启用导致阵列崩溃的数据恢复案例
服务器存储数据恢复环境: 一台EMC某型号存储中有一组RAID5磁盘阵列。该raid5阵列中有12块硬盘,其中2块硬盘为热备盘。 服务器存储故障: 该存储raid5阵列中有两块硬盘离线,只有1块热备盘启用替换掉其中一块离线盘,另外…...

HTML—css
css概述 C S S 是 C a s c a d i n g S t y l e S h e e t s ( 级 联 样 式 表 ) 。 C S S 是 一 种 样 式 表 语 言 , 用 于 为 H T M L 文 档 控 制 外 观 , 定 义 布 局 。 例 如 , C S S 涉 及 字 体 、 颜 色 、…...
)
IO多路复用(Input/Output Multiplexing)
IO多路复用(Input/Output Multiplexing) 是一种在单个线程中管理多个输入/输出通道的技术。它允许一个线程同时监听多个输入流(如网络套接字、文件描述符等),并在有数据可读或可写时进行相应的处理,而不需要为每个通道创建一个独立的线程。这种技术主要用于处理并发连接…...

android与pc 用socket无线通信
今天做一个android与pc通信的小demo(不是wifi,蓝牙)android为客户端,pc为服务器(一对多)。pc代码很简单,android客户端代码也不难,但是有一点不太明白就是在客户端向服务器发送消息时…...
【流程引擎】springboot完美集成activiti工作流方案
前言 activiti工作流引擎项目,企业erp、oa、hr、crm等企事业办公系统轻松落地,一套完整并且实际运用在多套项目中的案例,满足日常业务流程审批需求。 项目源码配套文档获取:本文末个人名片直接获取。 一、项目形式 springboot…...

11、常见API
01、String类概述及构造方法简介 一、字符串 由多个字符组成的一串数据 二、简介 String类代表的是一个字符串。字符串对象在开发中是最常见的。为了方便我们对字符串进行操作,java就把字符串用对象进行了封装,这个封装就是String类 三、String类的构造方…...

渗透第三次作业
目录 第一关Ma Spaghet! 第二关Jefff: 第三关:Ugandan Knuckles 第四关:Ricardo Milos 第五关: Ah Thats Hawt 第一关Ma Spaghet! <h2 id"spaghet"></h2> <script>spaghet.innerHTML (new URL(…...

Python自动化:解锁高效工作与生产力的密钥
在当今快节奏的数字时代,自动化已成为提升工作效率、优化流程、减少人为错误的不可或缺的工具。Python,作为一种功能强大、易于学习且应用广泛的编程语言,在自动化领域扮演着举足轻重的角色。无论是数据处理、Web自动化、软件测试,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
