激光雷达点云投影到图像平面

将激光雷达点云投影到图像平面涉及几何变换和相机模型的应用。以下是该过程的基本原理:
1. 坐标系转换
激光雷达生成的点云通常位于激光雷达的坐标系中,而图像则在相机坐标系中。为了将点云投影到图像上,首先需要将点云从激光雷达坐标系转换到相机坐标系。
假设激光雷达坐标系中的一个点表示为
[ X lidar , Y lidar , Z lidar ] [X_{\text{lidar}}, Y_{\text{lidar}}, Z_{\text{lidar}}] [Xlidar,Ylidar,Zlidar]
,我们使用一个外参矩阵 (T)(通常是一个4x4的齐次变换矩阵),将其转换到相机坐标系:
[ X cam Y cam Z cam 1 ] = T ⋅ [ X lidar Y lidar Z lidar 1 ] \begin{bmatrix} X_{\text{cam}} \\ Y_{\text{cam}} \\ Z_{\text{cam}} \\ 1 \end{bmatrix} =T \cdot \begin{bmatrix} X_{\text{lidar}} \\ Y_{\text{lidar}} \\ Z_{\text{lidar}} \\ 1 \end{bmatrix} XcamYcamZcam1 =T⋅ XlidarYlidarZlidar1
其中,(T) 包含了旋转和平移的信息。
2. 相机投影模型
在得到相机坐标系下的点云坐标 [ X cam , Y cam , Z cam ] [X_{\text{cam}}, Y_{\text{cam}}, Z_{\text{cam}}] [Xcam,Ycam,Zcam]后,下一步是将这些三维坐标投影到二维图像平面。相机投影通常使用针孔相机模型,其基本公式如下:
[ u v ] = 1 Z cam [ f x 0 c x 0 f y c y ] ⋅ [ X cam Y cam Z cam ] \begin{bmatrix} u \\ v \end{bmatrix} =\frac{1}{Z_{\text{cam}}} \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \end{bmatrix} \cdot \begin{bmatrix} X_{\text{cam}} \\ Y_{\text{cam}} \\ Z_{\text{cam}} \end{bmatrix} [uv]=Zcam1[fx00fycxcy]⋅ XcamYcamZcam
其中:
- (u) 和 (v) 是图像平面上的像素坐标。
- (f_x) 和 (f_y) 是相机的焦距(在像素单位下)。
- (c_x) 和 (c_y) 是图像中心的坐标(主点)。

3. 应用畸变校正(如果有)
相机镜头的畸变会导致投影后的点出现偏差,因此通常会应用畸变校正。常见的畸变包括径向畸变和切向畸变,可以通过预先计算的畸变系数来校正。
4. 点云到图像的映射
通过上述步骤,每个激光雷达点都可以在图像平面上找到一个对应的像素坐标 ((u, v))。这些像素坐标表示激光雷达点在图像中的投影位置。
在相机模型中, ( c_x ) 和 ( c_y ) 通常表示图像平面上的主点(principal point)的坐标。主点是相机光学中心在图像平面上的投影点,它通常接近图像的几何中心,但在实际相机中可能会有一些偏移。
详细解释:
-
主点 ( c_x, c_y ):这是图像平面上光轴与平面的交点的坐标,也称为光学中心。它通常由相机的内参矩阵(Intrinsic Matrix)中的两个参数表示。
-
相机内参矩阵:在相机标定过程中,我们可以得到一个 3x3 的内参矩阵,它的形式如下:
K = ( f x 0 c x 0 f y c y 0 0 1 ) K = \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix} K= fx000fy0cxcy1
其中:- f_x, f_y 是相机在 x 和 y 方向的焦距,通常与相机的焦距和像素大小相关。
- c_x, c_y 是主点的坐标。
相关文章:

激光雷达点云投影到图像平面
将激光雷达点云投影到图像平面涉及几何变换和相机模型的应用。以下是该过程的基本原理: 1. 坐标系转换 激光雷达生成的点云通常位于激光雷达的坐标系中,而图像则在相机坐标系中。为了将点云投影到图像上,首先需要将点云从激光雷达坐标系转换…...

[python]将anaconda默认创建环境python版本设置为32位的
首先看看gpt怎么回答的 装了Anaconda。如果尚未安装,可以从Anaconda官网下载适合你的操作系统的安装程序,并按照安装向导进行安装。 二、创建32位Python环境 在Anaconda中,你可以通过修改环境变量来尝试切换到32位模式(尽管这并…...
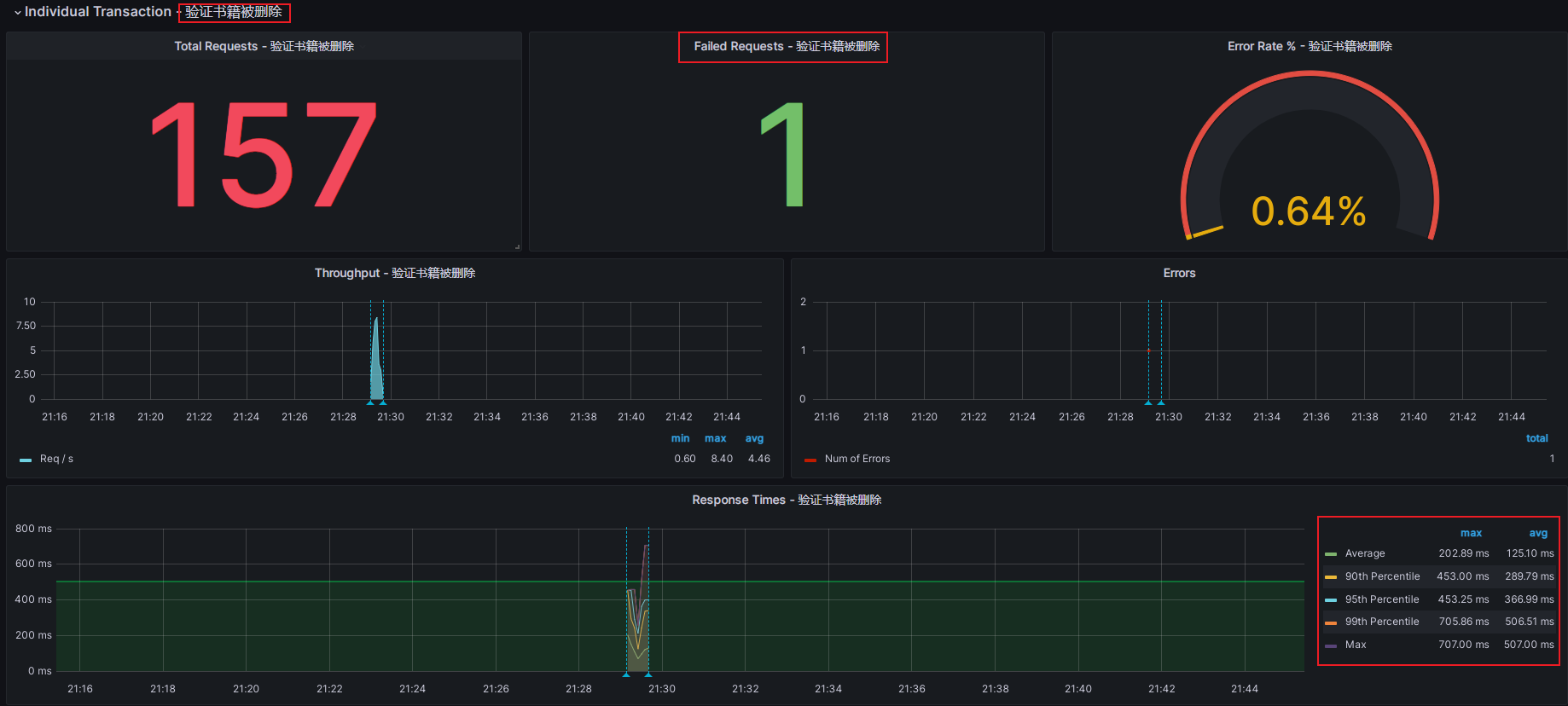
Jmeter+Influxdb+Grafana平台监控性能测试过程(三种方式)
一、Jmeter自带插件监控 下载地址:Install :: JMeter-Plugins.org 安装:下载后文件为jmeter-plugins-manager-1.3.jar,将其放入jmeter安装目录下的lib/ext目录,然后重启jmeter,即可。 启动Jmeter,测试计…...

[创业之路-135] :ERP、PDM、EDM、Git各种的用途和区别,硬件型初创公司需要哪些管理工具?
目录 前言: 一、ERP(企业资源计划) 二、PDM(产品数据管理系统) 三、EDM(文档管理系统,有时也指电子邮件营销) 四、Git 总结 五、硬件研发、生产型企业需要哪些管理工具&#…...
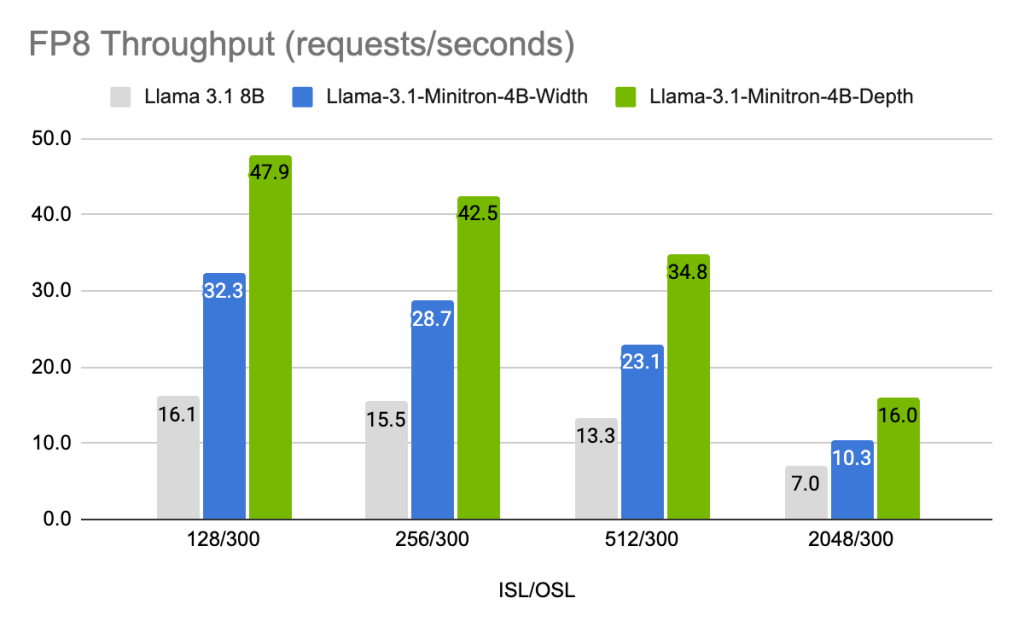
通过剪枝与知识蒸馏优化大型语言模型:NVIDIA在Llama 3.1模型上的实践与创新
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

DOM型xss靶场实验
xss是什么? XSS是一种经常出现在web应用中的计算机安全漏洞,它允许恶意web用户将代码植入到提供给其它用户使用的页面中。比如这些代码包括HTML代码和客户端脚本。攻击者利用XSS漏洞旁路掉访问控制--例如同源策略(same origin policy)。这种类型的漏洞由…...

华为---端口隔离简介和示例配置
目录 1. 端口隔离概念 2. 端口隔离作用 3. 端口隔离优点 4. 端口隔离缺点 5. 端口隔离的方法和应用场景 6. 端口隔离配置 6.1 端口隔离相关配置命令 6.2 端口隔离配置思路 7. 示例配置 7.1 示例场景 7.2 网络拓扑图 7.3 基本配置 7.4端口隔离配置与验证 7.4.1 双…...

Android 架构模式之 MVC
目录 架构设计的目的对 MVC 的理解Android 中 MVC 的问题试吃个小李子ViewModelController 大家好! 作为 Android 程序猿,MVC 应该是我们第一个接触的架构吧,从开始接触 Android 那一刻起,我们就开始接触它,可还记得我…...

节点使用简介:comfyui-photoshop
1、安装comfyui-photoshop 略过 一点要注意的是:在Photoshop上的安装增效工具,要通过Creative Cloud 桌面应用程序进行安装,才能成功在增效工具中显示,直接通过将文件解压到Plug-ins路径行不通(至少对我来说行不通&am…...
使用Go语言将PDF文件转换为Base64编码
使用 Go 语言将 Base64 编码转换为 PDF 文件-CSDN博客本文介绍了如何使用 Go 语言将 Base64 编码转换为 PDF 文件,并保存到指定路径。https://blog.csdn.net/qq_45519030/article/details/141225772 在现代编程中,数据转换和编码是常见的需求。本文将介绍…...

XSS Game
关卡网址:XSS Game - Learning XSS Made Simple! | Created by PwnFunction 1.Ma Spaghet! 见源代码分析得,somebody接收参数,输入somebody111查看所在位置 使用input标签 <input onmouseoveralert(1337)> 2.Jefff jeff接收参数,在ev…...
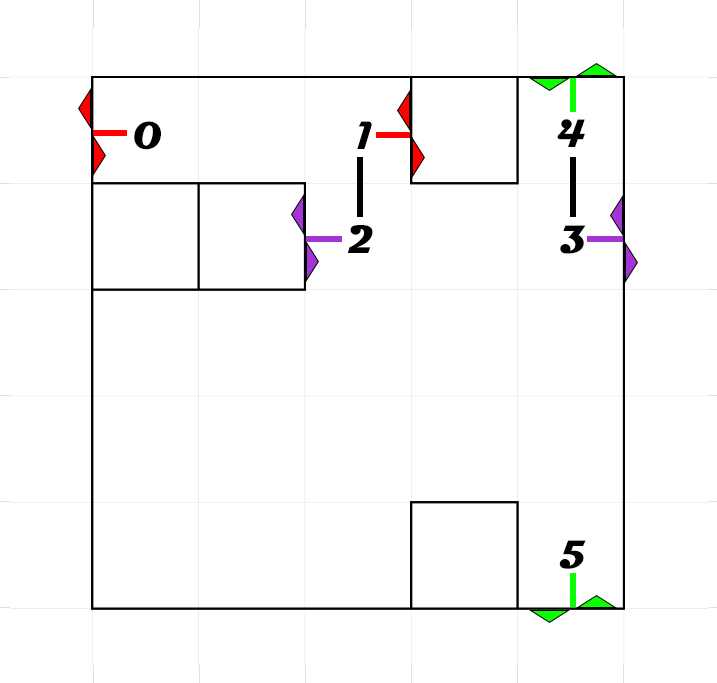
???牛客周赛55:虫洞操纵者
题目描述 \,\,\,\,\,\,\,\,\,\,你需要在一个可以上下左右移动的 nnn\times nnn 棋盘上解开一个迷宫:棋盘四周都是墙;每个方格要么是可以通过的空方格 ′0′\sf 0′0′ ,要么是不可通过的墙方格 ′1′\sf 1′1′ ;你可以沿着空方格…...

Unity3D开发之OnCollisionXXX触发条件
A和B碰撞触发OnCollision函数条件如下: 1.A和B都要有collider。(子物体有也可以) 2.A和B至少有一个刚体(Rigidbody)组件,且刚体的isKinematic为false。如果为true不会触发。 3.挂载脚本的物体必须有刚体…...

spfa()算法(求最短路)
spfa算法是对bellman_ford算法的优化,大部分求最短路问题都可以用spaf算法来求。 注意: (1)如若图中有负权回路,不能用spfa算法,要用bellman_ford算法;若只有负权边,则可以用 spf…...

聊聊国产数据库的生态系统建设
生态系统是指在自然界中,生物与环境构成统一的整体,之间相互影响相互制约,并在一定时期内处于相对稳定的动态平衡状态。所谓数据库的生态系统,从用户的角度看,就是充分打通产品使用过程中上下游的关联,使其…...
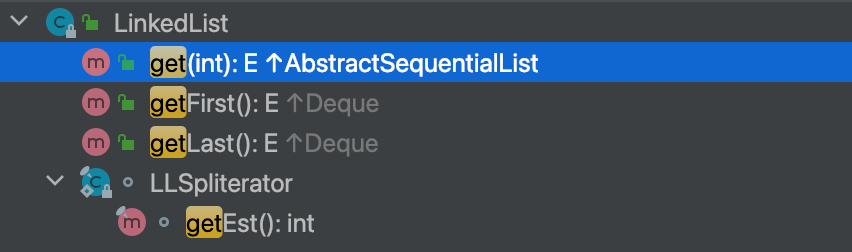
JDK源码解析:LinkedList
1、背景 我们咨询一下腾讯混元大模型,什么是“LinkedList”。 以下是混元大模型的回答: LinkedList 是 Java 集合框架中的一种数据结构,它实现了 List 和 Deque 接口。LinkedList 是一个双向链表,这意味着每个元素都包含对前一个和…...

drawio的问题
drawio的问题 先给出drawio的链接https://app.diagrams.net/ 我在用overleaf写论文的过程中,发现了一个问题,就是使用drawio画好图之后,只能保存以下几个选项: 但是不管是什么类型,在overleaf上面图片都不显示。如果…...

零基础学习Redis(3) -- Redis常用命令
Redis是一个 客户端-服务器 结构的程序,Redis客户端和服务器可以在同一台主机上,也可以在不同主机上,客户端和服务器之间通过网络进行通信。服务器端负责存储和管理数据。客户端则可以通过命名对服务端的数据进行操作。 Redis客户端有多种&a…...

响应式Web设计:纯HTML和CSS的实现技巧-1
响应式Web设计(Responsive Web Design, RWD)是一种旨在确保网站在不同设备和屏幕尺寸下都能良好运行的网页设计策略。通过纯HTML和CSS实现响应式设计,主要依赖于媒体查询(Media Queries)、灵活的布局、可伸缩的图片和字…...
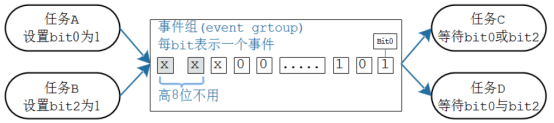
FrereRTOS事件组
文章目录 一、事件组概念与操作1、事件组的概念2、事件组的操作 二、事件组函数1、创建2、删除3、设置事件4、等待事件5、同步点 三、示例:广播四、示例:等待一个任意事件五、示例: 等待多个事件都发生 学校组织秋游,组长在等待: …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
