【分享】Excel的3个隐藏功能
我们在制作Excel表格的时候,有时候会包含一些敏感信息,为了确保这些数据的安全性,Excel提供了隐藏功能来保护工作表,下面小编分享3个Excel常用的隐藏功能,一起来看看如何设置吧!
功能一:隐藏部分数据
在处理身份证号、手机号等个人信息时,可以使用隐藏部分数据来保护个人信息。通过函数即可实现这个隐藏功能。
比如想要隐藏下图中手机号码的部分数据,首先在“手机号”后插入一列表格C列,然后在C2单元格里输入:=REPLACE(B2,4,4,"****"),就可以隐藏了,再把函数复制到其他单元格。
replace函数表示将一个字符串中的部分字符用另一个字符替换。
replace(要替换的字符串,开始位置,长度,新的字符串),更改括号里的内容可以调整隐藏内容。

功能二:隐藏公式
Excel表格中经常会用到数据函数,这些公式是默认可见的,如果不想被他人看到自己的计算思路和所用公式,可以通过密码将其隐藏起来。
以下图为例,看如何把“合计”里的公式隐藏起来。

首先,点击Excel表左上角的“三角形”图标,或者使用快捷键“Ctrl+A”,选中整个Excel表。

然后,通过快捷键“Ctrl+1”调出【设置单元格格式】对话框,在【保护】界面中,去除【锁定】前的“对钩”,再点击【确定】。

回到表格界面,选中需要隐藏公式的单元格。

再次使用快捷键“Ctrl+1”调出【设置单元格格式】对话框,在【保护】界面中,勾选【隐藏】选项,再点击【确定】。

回到表格界面,点击菜单选项卡【审阅】列表中【保护工作表】,弹出对话框后,在空白栏输入想要设置的密码,确认后再次输入一次,就设置好了。

可以看到,当鼠标选中公式单元格时,公式并没有显现出来。

如果后续需要取消隐藏,只需要点击菜单选项卡【审阅】列表中【撤销工作表保护】,然后在密码栏里输入原本设置的密码,再点击【确定】,就可以取消隐藏了。

需要注意的是,如果没有密码就无法在Excel里取消隐藏了,所以记得把密码记牢或者保存好。
要是不小心忘记了就需要借助其他工具的帮助,比如小编使用的Excel工具,可以不用密码,直接去除原本设置的保护。
首先点击工具里的【解除限制】模块,然后将Excel表格导入工具,即可一键解除。

功能三:隐藏行和列
如果需要隐藏Excel表中的某几行或列的全部数据,可以使用以下方法。
首先,选中需要隐藏的一整列或者一整行数据,然后点击鼠标右键,在列表中选择【隐藏】即可。

可以看到,选中的数据区域就会隐藏起来看不到了。

如果后续需要取消隐藏,只需要在表格界面点击鼠标右键,选择【取消隐藏】即可。

以上就是Excel的3种隐藏功能,你学会了吗?
相关文章:

【分享】Excel的3个隐藏功能
我们在制作Excel表格的时候,有时候会包含一些敏感信息,为了确保这些数据的安全性,Excel提供了隐藏功能来保护工作表,下面小编分享3个Excel常用的隐藏功能,一起来看看如何设置吧! 功能一:隐藏部分…...

Linux中的chown指令
chown(change owner)命令在 Linux 和其他类 Unix 系统中用于更改文件或目录的用户和/或组所有权。 基本用法 chown [选项] 用户名[:组名] 文件或目录 参数说明 用户名:指定新的文件或目录的所有者 组名:可选,指定新…...

UCOSIII内存管理机制详解
目录 前言 1. 内存管理概述 2. 内存区域(存储区)和内存块 3. 存储区控制块(OS_MEM) 4. 内存管理函数 5. 内存碎片问题 6. 注意事项 7.代码实现 7.1创建内存区域 7.2申请内存 7.3释放内存 前言 UCOSIII(即Mi…...

Android12 显示框架之Transaction----client端
目录:Android显示终极宝典 在前面的章节中,应用通过createSurface()在surfaceflinger中创建了一层layer,紧接着要做的事情就是对这个layer设置一些属性(或者叫状态),常设置的属性有位置、大小、z-order等等…...

在Windows上使用FRP搭建内网穿透:
FRP服务器端配置(公网服务器) 下载FRP: 访问FRP的GitHub发布页面:https://github.com/fatedier/frp/releases下载对应系统架构的frp_<version>_linux_amd64.tar.gz(如果你的服务器是Linux系统)或者f…...

TypeError: Cannot read properties of undefined (reading ‘scrollIntoView‘)(已解决)
问题复现:眨眼睛使用vitevue3实现跳转dom功能时使用了scrollIntoView方法,在打包上传以后使用该功能报错 小友可能会陷入误区,以为是函数方法有问题,毕竟在开发时是没有问题的, 而实际上呢问题出在获取节点失败了 在这…...

【解决】Unity Inspector 视窗脚本中文乱码问题
开发平台:Unity 2020 编程平台:Visual Studio 2022 问题描述 开发过程中,为便利化快速审阅代码内容,通过 Unity Inspector 确认代码内容与逻辑。但对于默认安装的 Visual Studio 编程平台,保存的 UTF- 8 脚本文件在…...

使用 C/C++访问 MySQL
目录 准备工作 尝试链接 MySQL Client MySQL 接口介绍 准备工作 保证 MySQL 服务有效。下载MySQL开发包(可以在MySQL官网下载安装也可以在软件源安装) MySQL 开发包通常会包含一些特定的头文件和库文件。您可以检查以下常见的路径: /us…...

Linux 网络套接字解析:实现网络通信
目录 一.网络基础1.协议2.OSI与TCP/IP模型3.网络通信流程4.IP与Mac地址 二.网络编程套接字1.端口号2.网络字节序3.tcp、udp协议4.socket编程5.sockaddr结构解析6.实现Udp_socket7.实现Windows与Linux通信8.Linux下远程执行指令9.实现tcp_socket10.守护进程 一.网络基础 1.协议…...

vue3 组合式API
<!-- 深度监听 deep 点击按钮控制台,才输出count变化了: 1, 老值: 0;否则控制台不输出 --> <script setup>import { ref,watch } from vueconst state ref({count:0})const setCount () > {state.count.value}watch(state, () > {console.log(…...

二、什么是Vue中的响应式?Vue的响应式原理
什么是Vue中的响应式 Vue中的响应式,简而言之就是当数据发生变化时,页面跟随变化。使用过Vue的v-model都有比较深刻的感受,我们在代码中修改双向绑定的数据后,页面上的数据也会自动更新,页面跟随变化 我们看个例子&am…...

快9月了才开始强化,跟张宇还是武忠祥?
快9月了才开始强化,跟张宇还是武忠祥! 说真的,我也替这位同学着急,但是考研数学越是进度慢,就越不能急!急着赶进度,容易出事!遇到这个问题的朋友肯定不止一位,那我就帮大…...

SSM好易学学习平台---附源码92142
摘 要 随着互联网趋势的到来,各行各业都在考虑利用互联网将自己推广出去,最好方式就是建立自己的互联网系统,并对其进行维护和管理。在现实运用中,应用软件的工作规则和开发步骤,采用Java技术建设好易学学习平台。本文…...

对于mp4 ios和mac safari不能播放问题处理
直接对原mp4文件进行重新转码就可以了 ffmpeg -i origin.mp4 -vcodec h264 -profile:v high -level 4.1 orgin_hl.mp4 原因源文件不符合苹果基本规则 苹果官网文档...

开发同城交友找搭子系统app前景分析
开发同城交友系统APP的背景 社交需求多样化: 随着城市化的加速和人们生活节奏的加快,现代人的社交圈子往往较为狭窄,难以结识新朋友。传统的线下交友方式受限于时间、地点等因素,难以满足现代人对于交友的多样化需求。互联网和智…...
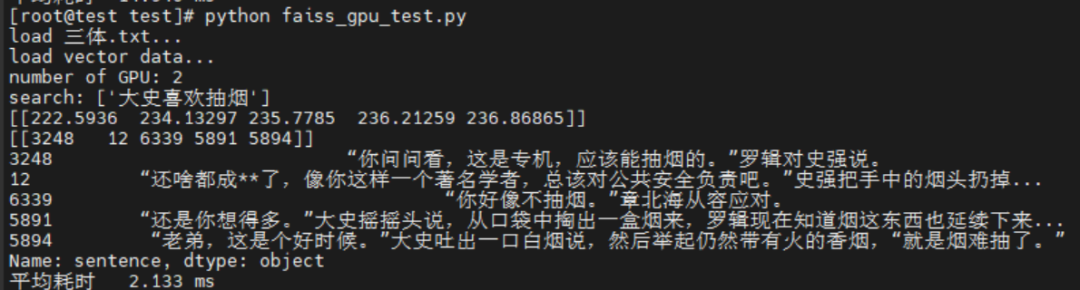
faiss向量数据库测试《三体》全集,这家国产AI加速卡,把性能提了7倍!
在人工智能和机器学习技术的飞速发展中,向量数据库在处理高维数据方面扮演着日益重要的角色。近年来,随着大型模型的流行,向量数据库技术也得到了进一步的发展和完善。 向量数据库为大型模型提供了一个高效的数据管理和检索平台,…...
)
负载均衡---相关概念介绍(一)
负载均衡(Load Balance)是集群技术的一种重要应用,旨在将负载(工作任务)进行平衡、分摊到多个操作单元上进行运行,从而提高系统的并发处理能力、增加吞吐量、加强网络处理能力,并提供故障转移以…...

计算机基础知识复习8.14
子线程抛异常主线程能否catch 在不做任何处理的情况下,主线程不能catch 解决方式: 子线程使用try catch来捕获异常 为线程设置未捕获异常处理器UncaughtExceptionHandler 通过future的get方法捕获异常 JVM相关参数 显示指定堆内存-Xms和-Xmx指定最…...

【io深层理解】
io深层理解 1.内核态2.用户态3. select IO多路复用执行原理4. select io多路复用限制和不足 1.内核态 一个进程会涉及多文件的修改,比如说。那么在内核态就会维护一个表,这个表叫文件描述符bitmap,这个表会传递给内核态,当然肯定传…...

【懒人工具】指定新文件,替换全盘旧文件
没辙,就是懒 最近在调整.clang-format,这个format文件要跟着项目走,只换本地默认的还不够。调整好以后一个项目一个项目的换,有时候会漏掉,索性全盘一次性换完。 基于自己操作的流程,写了个脚本࿰…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...
